ploeh blog danish software design
ASP.NET validation revisited
Is the built-in validation framework better than applicative validation?
I recently published an article called An applicative reservation validation example in C# in which I describe how to use the universal abstractions of applicative functors and semigroups to implement reusable, composable validation.
One reader reaction made me stop and think:
"An exercise on how to reject 90% of the framework's existing services (*Validation) only to re implement them more poorly, by renouncing standardization, interoperability and globalization all for the glory of FP."
(At the time of posting, the PopCatalin Twitter account's display name was Prime minister of truth™ カタリンポップ🇺🇦, which I find unhelpful. The linked GitHub account locates the user in Cluj-Napoca, a city I've repeatedly visited for conferences - the last time as recent as June 2022. I wouldn't be surprised if we've interacted, but if so, I'm sorry to say that I can't connect these accounts with one of the many wonderful people I've met there. In general, I'm getting a strong sarcastic vibe from that account, and I'm not sure whether or not to take Pronouns kucf/fof seriously. As the possibly clueless 51-year white male that I am, I will proceed with good intentions and to the best of my abilities.)
That reply is an important reminder that I should once in a while check my assumptions. I'm aware that the ASP.NET framework comes with validation features, but I many years ago dismissed them because I found them inadequate. Perhaps, in the meantime, these built-in services have improved to the point that they are to be preferred over applicative validation.
I decided to attempt to refactor the code to take advantage of the built-in ASP.NET validation to be able to compare the two approaches. This article is an experience report.
Requirements #
In order to compare the two approaches, the ASP.NET-based validation should support the same validation features as the applicative validation example:
- The
Atproperty is required and should be a valid date and time. If it isn't, the validation message should report the problem and the offending input. - The
Emailproperty should be required. If it's missing, the validation message should state so. - The
Quantityproperty is required and should be a natural number. If it isn't, the validation message should report the problem and the offending input.
The previous article includes an interaction example that I'll repeat here for convenience:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
Content-Type: application/json
{ "at": "large", "name": "Kerry Onn", "quantity": -1 }
HTTP/1.1 400 Bad Request
Invalid date or time: large.
Email address is missing.
Quantity must be a positive integer, but was: -1.
ASP.NET validation formats the errors differently, as you'll see later in this article. That's not much of a concern, though: Error messages are for other developers. They don't really have to be machine-readable or have a strict shape (as opposed to error types, which should be machine-readable).
Reporting the offending values, as in "Quantity must be a positive integer, but was: -1." is part of the requirements. A REST API can make no assumptions about its clients. Perhaps one client is an unattended batch job that only logs errors. Logging offending values may be helpful to maintenance developers of such a batch job.
Framework API #
The first observation to make about the ASP.NET validation API is that it's specific to ASP.NET. It's not a general-purpose API that you can use for other purposes.
If, instead, you need to validate input to a console application, a background message handler, a batch job, or a desktop or phone app, you can't use that API.
Perhaps each of these styles of software come with their own validation APIs, but even if so, that's a different API you'll have to learn. And in cases where there's no built-in validation API, then what do you do?
The beauty and practicality of applicative validation is that it's universal. Since it's based on mathematical foundations, it's not tied to a particular framework, platform, or language. These concepts exist independently of technology. Once you understand the concepts, they're always there for you.
The code example from the previous article, as well as here, build upon the code base that accompanies Code That Fits in Your Head. An example code base has to be written in some language, and I chose C# because I'm more familiar with it than I am with Java, C++, or TypeScript. While I wanted the code base to be realistic, I tried hard to include only coding techniques and patterns that you could use in more than one language.
As I wrote the book, I ran into many interesting problems and solutions that were specific to C# and ASP.NET. While I found them too specific to include in the book, I wrote a series of blog posts about them. This article is now becoming one of those.
The point about the previous article on applicative reservation validation in C# was to demonstrate how the general technique works. Not specifically in ASP.NET, or even C#, but in general.
It just so happens that this example is situated in a context where an alternative solution presents itself. This is not always the case. Sometimes you have to solve this problem yourself, and when this happens, it's useful to know that validation is a solved problem. Even so, while a universal solution exists, it doesn't follow that the universal solution is the best. Perhaps there are specialised solutions that are better, each within their constrained contexts.
Perhaps ASP.NET validation is an example of that.
Email validation #
The following is a report on my experience refactoring validation to use the built-in ASP.NET validation API.
I decided to start with the Email property, since the only requirement is that this value should be present. That seemed like an easy way to get started.
I added the [Required] attribute to the ReservationDto class' Email property. Since this code base also uses nullable reference types, it was necessary to also annotate the property with the [NotNull] attribute:
[Required, NotNull] public string? Email { get; set; }
That's not too difficult, and seems to be working satisfactorily:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
> content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 1
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|552ab5ff-494e1d1a9d4c6355.",
"errors": { "Email": [ "The Email field is required." ] }
}
As discussed above, the response body is formatted differently than in the applicative validation example, but I consider that inconsequential for the reasons I gave.
So far, so good.
Quantity validation #
The next property I decided to migrate was Quantity. This must be a natural number; that is, an integer greater than zero.
Disappointingly, no such built-in validation attribute seems to exist. One highly voted Stack Overflow answer suggested using the [Range] attribute, so I tried that:
[Range(1, int.MaxValue, ErrorMessage = "Quantity must be a natural number.")] public int Quantity { get; set; }
As a declarative approach to validation goes, I don't think this is off to a good start. I like declarative programming, but I'd prefer to be able to declare that Quantity must be a natural number, rather than in the range of 1 and int.MaxValue.
Does it work, though?
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|d9a6be38-4be82ede7c525913.",
"errors": {
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a natural number." ]
}
}
While it does capture the intent that Quantity must be one or greater, it fails to echo back the offending value.
In order to address that concern, I tried reading the documentation to find a way forward. Instead I found this:
"Internally, the attributes call String.Format with a placeholder for the field name and sometimes additional placeholders. [...]"
"To find out which parameters are passed to
String.Formatfor a particular attribute's error message, see the DataAnnotations source code."
Really?!
If you have to read implementation code, encapsulation is broken.
Hardly impressed, I nonetheless found the RangeAttribute source code. Alas, it only passes the property name, Minimum, and Maximum to string.Format, but not the offending value:
return string.Format(CultureInfo.CurrentCulture, ErrorMessageString, name, Minimum, Maximum);
This looked like a dead end, but at least it's possible to extend the ASP.NET validation API:
public sealed class NaturalNumberAttribute : ValidationAttribute { protected override ValidationResult IsValid( object value, ValidationContext validationContext) { if (validationContext is null) throw new ArgumentNullException(nameof(validationContext)); var i = value as int?; if (i.HasValue && 0 < i) return ValidationResult.Success; return new ValidationResult( $"{validationContext.MemberName} must be a positive integer, but was: {value}."); } }
Adding this NaturalNumberAttribute class enabled me to change the annotation of the Quantity property:
[NaturalNumber] public int Quantity { get; set; }
This seems to get the job done:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|bb45b60d-4bd255194871157d.",
"errors": {
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a positive integer, but was: 0." ]
}
}
The [NaturalNumber] attribute now correctly reports the offending value together with a useful error message.
Compare, however, the above NaturalNumberAttribute class to the TryParseQuantity function, repeated here for convenience:
private Validated<string, int> TryParseQuantity() { if (Quantity < 1) return Validated.Fail<string, int>( $"Quantity must be a positive integer, but was: {Quantity}."); return Validated.Succeed<string, int>(Quantity); }
TryParseQuantity is shorter and has half the cyclomatic complexity of NaturalNumberAttribute. In isolation, at least, I'd prefer the shorter, simpler alternative.
Date and time validation #
Remaining is validation of the At property. As a first step, I converted the property to a DateTime value and added attributes:
[Required, NotNull] public DateTime? At { get; set; }
I'd been a little apprehensive doing that, fearing that it'd break a lot of code (particularly tests), but that turned out not to be the case. In fact, it actually simplified a few of the tests.
On the other hand, this doesn't really work as required:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|1e1d600e-4098fb36635642f6.",
"errors": {
"dto": [ "The dto field is required." ],
"$.at": [ "The JSON value could not be converted to System.Nullable`1[System.DateTime].↩
Path: $.at | LineNumber: 0 | BytePositionInLine: 26." ]
}
}
(I've wrapped the last error message over two lines for readability. The ↩ symbol indicates where I've wrapped the text.)
There are several problems with this response. First, in addition to complaining about the missing at property, it should also have reported that there are problems with the Quantity and that the Email property is missing. Instead, the response implies that the dto field is missing. That's likely confusing to client developers, because dto is an implementation detail; it's the name of the C# parameter of the method that handles the request. Client developers can't and shouldn't know this. Instead, it looks as though the REST API somehow failed to receive the JSON document that the client posted.
Second, the error message exposes other implementation details, here that the at field has the type System.Nullable`1[System.DateTime]. This is, at best, irrelevant. At worst, it could be a security issue, because it reveals to a would-be attacker that the system is implemented on .NET.
Third, the framework rejects what looks like a perfectly good date and time: 2022-11-21 19:00. This is a breaking change, since the API used to accept such values.
What's wrong with 2022-11-21 19:00? It's not a valid ISO 8601 string. According to the ISO 8601 standard, the date and time must be separated by T:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21T19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|1e1d600f-4098fb36635642f6.",
"errors": {
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a positive integer, but was: 0." ]
}
}
Posting a valid ISO 8601 string does, indeed, enable the client to proceed - only to receive a new set of error messages. After I converted At to DateTime?, the ASP.NET validation framework fails to collect and report all errors. Instead it stops if it can't parse the At property. It doesn't report any other errors that might also be present.
That is exactly the requirement that applicative validation so elegantly solves.
Tolerant Reader #
While it's true that 2022-11-21 19:00 isn't valid ISO 8601, it's unambiguous. According to Postel's law an API should be a Tolerant Reader. It's not.
This problem, however, is solvable. First, add the Tolerant Reader:
public sealed class DateTimeConverter : JsonConverter<DateTime> { public override DateTime Read( ref Utf8JsonReader reader, Type typeToConvert, JsonSerializerOptions options) { return DateTime.Parse( reader.GetString(), CultureInfo.InvariantCulture); } public override void Write( Utf8JsonWriter writer, DateTime value, JsonSerializerOptions options) { if (writer is null) throw new ArgumentNullException(nameof(writer)); writer.WriteStringValue(value.ToString("s")); } }
Then add it to the JSON serialiser's Converters:
opts.JsonSerializerOptions.Converters.Add(new DateTimeConverter());
This, at least, addresses the Tolerant Reader concern:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|11576943-400dafd4b489c282.",
"errors": {
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a positive integer, but was: 0." ]
}
}
The API now accepts the slightly malformed at field. It also correctly handles if the field is entirely missing:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|11576944-400dafd4b489c282.",
"errors": {
"At": [ "The At field is required." ],
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a positive integer, but was: 0." ]
}
}
On the other hand, it still doesn't gracefully handle the case when the at field is unrecoverably malformed:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "foo",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|11576945-400dafd4b489c282.",
"errors": {
"": [ "The supplied value is invalid." ],
"dto": [ "The dto field is required." ]
}
}
The supplied value is invalid. and The dto field is required.? That's not really helpful. And what happened to The Email field is required. and Quantity must be a positive integer, but was: 0.?
If there's a way to address this problem, I don't know how. I've tried adding another custom attribute, similar to the above NaturalNumberAttribute class, but that doesn't solve it - probably because the model binder (that deserialises the JSON document to a ReservationDto instance) runs before the validation.
Perhaps there's a way to address this problem with yet another class that derives from a base class, but I think that I've already played enough Whack-a-mole to arrive at a conclusion.
Conclusion #
Your context may differ from mine, so the conclusion that I arrive at may not apply in your situation. For example, I'm given to understand that one benefit that the ASP.NET validation framework provides is that when used with ASP.NET MVC (instead of as a Web API), (some of) the validation logic can also run in JavaScript in browsers. This, ostensibly, reduces code duplication.
"Yet in the case of validation, a Declarative model is far superior to a FP one. The declarative model allows various environments to implement validation as they need it (IE: Client side validation) while the FP one is strictly limited to the environment executing the code."
On the other hand, using the ASP.NET validation framework requires more code, and more complex code, than with applicative validation. It's a particular set of APIs that you have to learn, and that knowledge doesn't transfer to other frameworks, platforms, or languages.
Apart from client-side validation, I fail to see how applicative validation "re implement[s validation] more poorly, by renouncing standardization, interoperability and globalization".
I'm not aware that there's any standard for validation as such, so I think that @PopCatalin has the 'standard' ASP.NET validation API in mind. If so, I consider applicative validation a much more standardised solution than a specialised API.
If by interoperability @PopCatalin means the transfer of logic from server side to client side, then it's true that the applicative validation I showed in the previous article runs exclusively on the server. I wonder, however, how much of such custom validation as NaturalNumberAttribute automatically transfers to the client side.
When it comes to globalisation, I fail to see how applicative validation is less globalisable than the ASP.NET validation framework. One could easily replace the hard-coded strings in my examples with resource strings.
It would seem, again, that any sufficiently complicated custom validation framework contains an ad-hoc, informally-specified, bug-ridden, slow implementation of half of applicative validation.
"I must admit I really liked the declarative OOP model using annotations when I first saw it in Java (EJB3.0, almost 20yrs ago) until I saw FP way of doing things. FP way is so much simpler and powerful, because it's just function composition, nothing more, no hidden "magic"."
I still find myself in the same camp as Witold Szczerba. It's easy to get started using validation annotations, but it doesn't follow that it's simpler or better in the long run. As Rich Hickey points out in Simple Made Easy, simple and easy isn't the same. If I have to maintain code, I'll usually choose the simple solution over the easy solution. That means choosing applicative validation over a framework-specific validation API.
Endomorphism as an invariant functor
An article (also) for object-oriented programmers.
This article is part of a series of articles about invariant functors. An invariant functor is a functor that is neither covariant nor contravariant. See the series introduction for more details.
An endomorphism is a function where the return type is the same as the input type.
In Haskell we denote an endomorphism as a -> a, in F# we have to add an apostrophe: 'a -> 'a, while in C# such a function corresponds to the delegate Func<T, T> or, alternatively, to a method that has the same return type as input type.
In Haskell you can treat an endomorphism like a monoid by wrapping it in a container called Endo: Endo a. In C#, we might model it as an interface called IEndomorphism<T>.
That looks enough like a functor that you might wonder if it is one, but it turns out that it's neither co- nor contravariant. You can deduce this with positional variance analysis (which I've learned from Thinking with Types). In short, this is because T appears as both input and output - it's neither co- nor contravariant, but rather invariant.
Explicit endomorphism interface in C# #
Consider an IEndomorphism<T> interface in C#:
public interface IEndomorphism<T> { T Run(T x); }
I've borrowed this interface from the article From State tennis to endomorphism. In that article I explain that I only introduce this interface for educational reasons. I don't expect you to use something like this in production code bases. On the other hand, everything that applies to IEndomorphism<T> also applies to 'naked' functions, as you'll see later in the article.
As outlined in the introduction, you can make a container an invariant functor by implementing a non-standard version of Select:
public static IEndomorphism<B> Select<A, B>( this IEndomorphism<A> endomorphism, Func<A, B> aToB, Func<B, A> bToA) { return new SelectEndomorphism<A, B>(endomorphism, aToB, bToA); } private class SelectEndomorphism<A, B> : IEndomorphism<B> { private readonly IEndomorphism<A> endomorphism; private readonly Func<A, B> aToB; private readonly Func<B, A> bToA; public SelectEndomorphism( IEndomorphism<A> endomorphism, Func<A, B> aToB, Func<B, A> bToA) { this.endomorphism = endomorphism; this.aToB = aToB; this.bToA = bToA; } public B Run(B x) { return aToB(endomorphism.Run(bToA(x))); } }
Since the Select method has to return an IEndomorphism<B> implementation, one option is to use a private, nested class. Most of this is ceremony required because it's working with interfaces. The interesting part is the nested class' Run implementation.
In order to translate an IEndomorphism<A> to an IEndomorphism<B>, the Run method first uses bToA to translate x to an A value. Once it has the A value, it can Run the endomorphism, which returns another A value. Finally, the method can use aToB to convert the returned A value to a B value that it can return.
Here's a simple example. Imagine that you have an endomorphism like this one:
public sealed class Incrementer : IEndomorphism<BigInteger> { public BigInteger Run(BigInteger x) { return x + 1; } }
This one simply increments a BigInteger value. Since BigInteger is isomorphic to a byte array, it's possible to transform this BigInteger endomorphism to a byte array endomorphism:
[Theory] [InlineData(new byte[0], new byte[] { 1 })] [InlineData(new byte[] { 1 }, new byte[] { 2 })] [InlineData(new byte[] { 255, 0 }, new byte[] { 0, 1 })] public void InvariantSelection(byte[] bs, byte[] expected) { IEndomorphism<BigInteger> source = new Incrementer(); IEndomorphism<byte[]> destination = source.Select(bi => bi.ToByteArray(), arr => new BigInteger(arr)); Assert.Equal(expected, destination.Run(bs)); }
You can convert a BigInteger to a byte array with the ToByteArray method, and convert such a byte array back to a BigInteger using one of its constructor overloads. Since this is possible, the example test can convert this IEndomorphism<BigInteger> to an IEndomorphism<byte[]> and later Run it.
Mapping functions in F# #
You don't need an interface in order to turn an endomorphism into an invariant functor. An endomorphism is just a function that has the same input and output type. In C# such a function has the type Func<T, T>, while in F# it's written 'a -> 'a.
You could write an F# module that defines an invmap function, which would be equivalent to the above Select method:
module Endo = // ('a -> 'b) -> ('b -> 'a) -> ('a -> 'a) -> ('b -> 'b) let invmap (f : 'a -> 'b) (g : 'b -> 'a) (h : 'a -> 'a) = g >> h >> f
Since this function doesn't have to deal with the ceremony of interfaces, the implementation is simple function composition: For any input, first apply it to the g function, then apply the output to the h function, and again apply the output of that function to the f function.
Here's the same example as above:
let increment (bi : BigInteger) = bi + BigInteger.One // byte [] -> byte [] let bArrInc = Endo.invmap (fun (bi : BigInteger) -> bi.ToByteArray ()) BigInteger increment
Here's a simple sanity check of the bArrInc function executed in F# Interactive:
> let bArr = bArrInc [| 255uy; 255uy; 0uy |];; val bArr : byte [] = [|0uy; 0uy; 1uy|]
If you are wondering about that particular output value, I'll refer you to the BigInteger documentation.
Function composition #
The F# implementation of invmap (g >> h >> f) makes it apparent that an endomorphism is an invariant functor via function composition. In F#, though, that fact almost disappears in all the type declaration ceremony. In the Haskell instance from the invariant package it's even clearer:
instance Invariant Endo where invmap f g (Endo h) = Endo (f . h . g)
Perhaps a diagram is helpful:
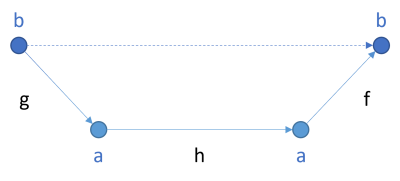
If you have a function h from the type a to a and you need a function b -> b, you can produce it by putting g in front of h, and f after. That's also what the above C# implementation does. In F#, you can express such a composition as g >> h >> f, which seems natural to most westerners, since it goes from left to right. In Haskell, most expressions are instead expressed from right to left, so it becomes: f . h . g. In any case, the result is the desired function that takes a b value as input and returns a b value as output. That composed function is indicated by a dashed arrow in the above diagram.
Identity law #
Contrary to my usual habit, I'm going to prove that both invariant functor laws hold for this implementation. I'll use equational reasoning with the notation that Bartosz Milewski uses. Here's the proof that the invmap instance obeys the identity law:
invmap id id (Endo h)
= { definition of invmap }
Endo (id . h . id)
= { eta expansion }
Endo (\x -> (id . h . id) x)
= { defintion of composition (.) }
Endo (\x -> id (h (id x)))
= { defintion of id }
Endo (\x -> h x)
= { eta reduction }
Endo h
= { definition of id }
id (Endo h)
While I'm not going to comment further on that, I can show you what the identity law looks like in C#:
[Theory] [InlineData(0)] [InlineData(1)] [InlineData(9)] public void IdentityLaw(long l) { IEndomorphism<BigInteger> e = new Incrementer(); IEndomorphism<BigInteger> actual = e.Select(x => x, x => x); Assert.Equal(e.Run(l), actual.Run(l)); }
In C#, you typically write the identity function (id in F# and Haskell) as the lambda expression x => x, since the identity function isn't 'built in' for C# like it is for F# and Haskell. (You can define it yourself, but it's not as idiomatic.)
Composition law #
As with the identity law, I'll start by suggesting a proof for the composition law for the Haskell instance:
invmap f2 f2' $ invmap f1 f1' (Endo h)
= { definition of invmap }
invmap f2 f2' $ Endo (f1 . h . f1')
= { defintion of ($) }
invmap f2 f2' (Endo (f1 . h . f1'))
= { definition of invmap }
Endo (f2 . (f1 . h . f1') . f2')
= { associativity of composition (.) }
Endo ((f2 . f1) . h . (f1' . f2'))
= { definition of invmap }
invmap (f2 . f1) (f1' . f2') (Endo h)
As above, a C# example may also help. First, assume that you have some endomorphism like this:
public sealed class SecondIncrementer : IEndomorphism<TimeSpan> { public TimeSpan Run(TimeSpan x) { return x + TimeSpan.FromSeconds(1); } }
A test then demonstrates the composition law in action:
[Theory] [InlineData(-3)] [InlineData(0)] [InlineData(11)] public void CompositionLaw(long x) { IEndomorphism<TimeSpan> i = new SecondIncrementer(); Func<TimeSpan, long> f1 = ts => ts.Ticks; Func<long, TimeSpan> f1p = l => new TimeSpan(l); Func<long, IntPtr> f2 = l => new IntPtr(l); Func<IntPtr, long> f2p = ip => ip.ToInt64(); IEndomorphism<IntPtr> left = i.Select(f1, f1p).Select(f2, f2p); IEndomorphism<IntPtr> right = i.Select(ts => f2(f1(ts)), ip => f1p(f2p(ip))); Assert.Equal(left.Run(new IntPtr(x)), right.Run(new IntPtr(x))); }
Don't try to make any sense of this. As outlined in the introductory article, in order to use an invariant functor, you're going to need an isomorphism. In order to demonstrate the composition law, you need three types that are isomorphic. Since you can convert back and forth between TimeSpan and IntPtr via long, this requirement is formally fulfilled. It doesn't make any sense to add a second to a value and then turn it into a function that changes a pointer. It sounds more like a security problem waiting to happen... Don't try this at home, kids.
Conclusion #
Since an endomorphism can be modelled as a 'generic type', it may look like a candidate for a functor or contravariant functor, but alas, neither is possible. The best we can get (apart from a monoid instance) is an invariant functor.
The invariant functor instance for an endomorphism turns out to be simple function composition. That's not how all invariant functors, work, though.
Invariant functors
Containers that support mapping isomorphic values.
This article series is part of a larger series of articles about functors, applicatives, and other mappable containers. So far, you've seen examples of both co- and contravariant functors, including profunctors. You've also seen a few examples of monomorphic functors - mappable containers where there's no variance at all.
What happens, on the other hand, if you have a container of (generic) values, but it's neither co- nor contravariant? An endomorphism is an example - it's neither co- nor contravariant. You'll see a treatment of that in a later article.
Even if neither co- nor contravariant mappings exists for a container, all may not be lost. It may still be an invariant functor.
Invariance #
Consider a container f (for functor). Depending on its variance, we call it covariant, contravariant, or invariant:
- Covariance means that any function
a -> bcan be lifted into a functionf a -> f b. - Contravariance means that any function
a -> bcan be lifted into a functionf b -> f a. - Invariance means that in general, no function
a -> bcan be lifted into a function overf a.
In general, that is. A limited escape hatch exists:
"an invariant type [...] allows you to map from
atobif and only ifaandbare isomorphic. In a very real sense, this isn't an interesting property - an isomorphism betweenaandbmeans they're already the same thing to begin with."
In Haskell we may define an invariant functor (AKA exponential functor) as in the invariant package:
class Invariant f where invmap :: (a -> b) -> (b -> a) -> f a -> f b
This means that an invariant functor f is a container of values where a translation from f a to f b exists if it's possible to translate contained values both ways: From a to b, and from b to a. Callers of the invmap function must supply translations that go both ways.
Invariant functor in C# #
It's possible to translate the concept to a language like C#. Since C# doesn't have higher-kinded types, we have to examine the abstraction as a set of patterns or templates. For functors and monads, the C# compiler can perform 'compile-time duck typing' to recognise these motifs to enable query syntax. For more advanced or exotic universal abstractions, such as bifunctors, profunctors, or invariant functors, we have to use a concrete container type as a stand-in for 'any' functor. In this article, I'll call it Invariant<A>.
Such a generic class must have a mapping function that corresponds to the above invmap. In C# it has this signature:
public Invariant<B> InvMap<B>(Func<A, B> aToB, Func<B, A> bToA)
In this example, InvMap is an instance method on Invariant<A>. You may use it like this:
Invariant<long> il = createInvariant(); Invariant<TimeSpan> its = il.InvMap(l => new TimeSpan(l), ts => ts.Ticks);
It's not that easy to find good examples of truly isomorphic primitives, but TimeSpan is just a useful wrapper of long, so it's possible to translate back and forth without loss of information. To create a TimeSpan from a long, you can use the suitable constructor overload. To get a long from a TimeSpan, you can read the Ticks property.
Perhaps you find a method name like InvMap non-idiomatic in C#. Perhaps a more idiomatic name might be Select? That's not a problem:
public Invariant<B> Select<B>(Func<A, B> aToB, Func<B, A> bToA) { return InvMap(aToB, bToA); }
In that case, usage would look like this:
Invariant<long> il = createInvariant(); Invariant<TimeSpan> its = il.Select(l => new TimeSpan(l), ts => ts.Ticks);
In this article, I'll use Select in order to be consistent with C# naming conventions. Using that name, however, will not make query syntax light up. While the name is fine, the signature is not one that the C# compiler will recognise as enabling special syntax. The name does, however, suggest a kinship with a normal functor, where the mapping in C# is called Select.
Laws #
As is usual with these kinds of universal abstractions, an invariant functor must satisfy a few laws.
The first one we might call the identity law:
invmap id id = id
This law corresponds to the first functor law. When performing the mapping operation, if the values in the invariant functor are mapped to themselves, the result will be an unmodified functor.
In C# such a mapping might look like this:
var actual = i.Select(x => x, x => x);
The law then says that actual should be equal to i.
The second law we might call the composition law:
invmap f2 f2' . invmap f1 f1' = invmap (f2 . f1) (f1' . f2')
Granted, this looks more complicated, but also directly corresponds to the second functor law. If two sequential mapping operations are performed one after the other, the result should be the same as a single mapping operation where the functions are composed.
In C# the left-hand side might look like this:
Invariant<IntPtr> left = i.Select(f1, f1p).Select(f2, f2p);
In C# you can't name functions or variables with a quotation mark (like the Haskell code's f1' and f2'), so instead I named them f1p and f2p (with a p for prime).
Likewise, the right-hand side might look like this:
Invariant<IntPtr> right = i.Select(ts => f2(f1(ts)), ip => f1p(f2p(ip)));
The composition law says that the left and right values must be equal.
You'll see some more detailed examples in later articles.
Examples #
This is all too abstract to seem useful in itself, so example are warranted. You'll be able to peruse examples of specific invariant functors in separate articles:
- Endomorphism as an invariant functor
- Natural transformations as invariant functors
- Functors as invariant functors
- Contravariant functors as invariant functors
As two of the titles suggest, all functors are also invariant functors, and the same goes for contravariant functors:
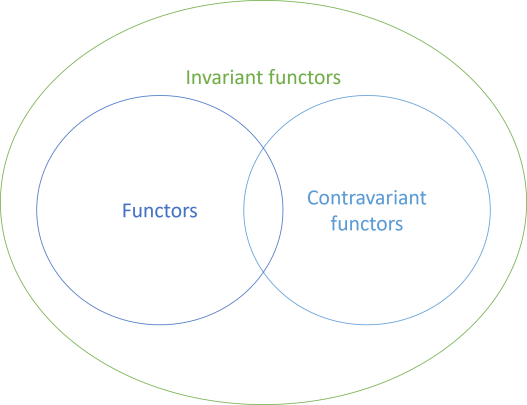
To be honest, invariant functors are exotic, and you are unlikely to need them in all but the rarest cases. Still, I did run into a scenario where I needed an invariant functor instance to be able to perform a particular sleight of hand. The rabbit holes we sometimes fall into...
Conclusion #
Invariant functors form a set that contains both co- and contravariant functors, as well as some data structures that are neither. This is an exotic abstraction that you may never need. It did, however, get me out of a bind at one time.
Next: Endomorphism as an invariant functor.Comments
For functors and monads, the C# compiler can perform 'compile-time duck typing' to recognise these motifs to enable query syntax.
Instead of 'compile-time duck typing', I think a better phrase to describe this is structural typing.
Tyson, thank you for writing. I wasn't aware of the term structural typing, so thank you for the link. I've now read that Wikipedia article, but all I know is what's there. Based on it, though, it looks as though F#'s Statically Resolved Type Parameters are another example of structural typing, in addition to the OCaml example given in the article.
IIRC, PureScript's row polymorphism may be another example, but it's been many years since I played with it. In other words, I could be mistaken.
Based on the Wikipedia article, it looks as though structural typing is more concerned with polymorphism, but granted, so is duck typing. Given how wrong 'compile-time duck typing' actually is in the above context, 'structural typing' seems more correct.
I may still stick with 'compile-time duck typing' as a loose metaphor, though, because most people know what duck typing is, whereas I'm not sure as many people know of structural typing. The purpose of the metaphor is, after all, to be helpful.
An applicative reservation validation example in C#
How to return all relevant error messages in a composable way.
I've previously suggested that I consider validation a solved problem. I still do, until someone disproves me with a counterexample. Here's a fairly straightforward applicative validation example in C#.
After corresponding and speaking with readers of Code That Fits in Your Head I've learned that some readers have objections to the following lines of code:
Reservation? reservation = dto.Validate(id); if (reservation is null) return new BadRequestResult();
This code snippet demonstrates how to parse, not validate, an incoming Data Transfer Object (DTO). This code base uses C#'s nullable reference types feature to distinguish between null and non-null objects. Other languages (and earlier versions of C#) can instead use the Maybe monad. Nothing in this article or the book hinges on the nullable reference types feature.
If the Validate method (which I really should have called TryParse instead) returns a null value, the Controller from which this code snippet is taken returns a 400 Bad Request response.
The Validate method is an instance method on the DTO class:
internal Reservation? Validate(Guid id) { if (!DateTime.TryParse(At, out var d)) return null; if (Email is null) return null; if (Quantity < 1) return null; return new Reservation( id, d, new Email(Email), new Name(Name ?? ""), Quantity); }
What irks some readers is the loss of information. While Validate 'knows' why it's rejecting a candidate, that information is lost and no error message is communicated to unfortunate HTTP clients.
One email from a reader went on about this for quite some time and I got the impression that the sender considered this such a grave flaw that it invalidates the entire book.
That's not the case.
Rabbit hole, evaded #
When I wrote the code like above, I was fully aware of trade-offs and priorities. I understood that this particular design would mean that clients get no information about why a particular reservation JSON document is rejected - only that it is.
This was a simplification that I explicitly decided to make for educational reasons.
The above design is based on something as simple as a null check. I expect all my readers to be able to follow that code. As hinted above, you could also model a method like Validate with the Maybe monad, but while Maybe preserves success cases, it throws away all information about errors. In a production system, this is rarely acceptable, but I found it acceptable for the example code in the book, since this isn't the main topic.
Instead of basing the design on nullable reference types or the Maybe monad, you can instead base parsing on applicative validation. In order to explain that, I'd first need to explain functors, applicative functors, and applicative validation. It might also prove helpful to the reader to explain Church encodings, bifunctors, and semigroups. That's quite a rabbit hole to fall into, and I felt that it would be such a big digression from the themes of the book that I decided not to go there.
On this blog, however, I have all the space and time I'd like. I can digress as much as I'd like. Most of that digression has already happened. Those articles are already on the blog. I'm going to assume that you've read all of the articles I just linked, or that you understand these concepts.
In this article, I'm going to rewrite the DTO parser to also return error messages. It's an entirely local change that breaks no existing tests.
Validated #
Most functional programmers are already aware of the Either monad. They often reach for it when they need to expand the Maybe monad with an error track.
The problem with the Either monad is, however, that it short-circuits error handling. It's like throwing exceptions. As soon as an Either composition hits the first error, it stops processing the rest of the data. As a caller, you only get one error message, even if there's more than one thing wrong with your input value.
In a distributed system where a client posts a document to a service, you'd like to respond with a collection of errors.
You can do this with a data type that's isomorphic with Either, but behaves differently as an applicative functor. Instead of short-circuiting on the first error, it collects them. This, however, turns out to be incompatible to the Either monad's short-circuiting behaviour, so this data structure is usually not given monadic features.
This data type is usually called Validation, but when I translated that to C# various static code analysis rules lit up, claiming that there was already a referenced namespace called Validation. Instead, I decided to call the type Validated<F, S>, which I like better anyway.
The type arguments are F for failure and S for success. I've put F before S because by convention that's how Either works.
I'm using an encapsulated variation of a Church encoding and a series of Apply overloads as described in the article An applicative password list. There's quite a bit of boilerplate, so I'll just dump the entire contents of the file here instead of tiring you with a detailed walk-through:
public sealed class Validated<F, S> { private interface IValidation { T Match<T>(Func<F, T> onFailure, Func<S, T> onSuccess); } private readonly IValidation imp; private Validated(IValidation imp) { this.imp = imp; } internal static Validated<F, S> Succeed(S success) { return new Validated<F, S>(new Success(success)); } internal static Validated<F, S> Fail(F failure) { return new Validated<F, S>(new Failure(failure)); } public T Match<T>(Func<F, T> onFailure, Func<S, T> onSuccess) { return imp.Match(onFailure, onSuccess); } public Validated<F1, S1> SelectBoth<F1, S1>( Func<F, F1> selectFailure, Func<S, S1> selectSuccess) { return Match( f => Validated.Fail<F1, S1>(selectFailure(f)), s => Validated.Succeed<F1, S1>(selectSuccess(s))); } public Validated<F1, S> SelectFailure<F1>( Func<F, F1> selectFailure) { return SelectBoth(selectFailure, s => s); } public Validated<F, S1> SelectSuccess<S1>( Func<S, S1> selectSuccess) { return SelectBoth(f => f, selectSuccess); } public Validated<F, S1> Select<S1>( Func<S, S1> selector) { return SelectSuccess(selector); } private sealed class Success : IValidation { private readonly S success; public Success(S success) { this.success = success; } public T Match<T>( Func<F, T> onFailure, Func<S, T> onSuccess) { return onSuccess(success); } } private sealed class Failure : IValidation { private readonly F failure; public Failure(F failure) { this.failure = failure; } public T Match<T>( Func<F, T> onFailure, Func<S, T> onSuccess) { return onFailure(failure); } } } public static class Validated { public static Validated<F, S> Succeed<F, S>( S success) { return Validated<F, S>.Succeed(success); } public static Validated<F, S> Fail<F, S>( F failure) { return Validated<F, S>.Fail(failure); } public static Validated<F, S> Apply<F, T, S>( this Validated<F, Func<T, S>> selector, Validated<F, T> source, Func<F, F, F> combine) { if (selector is null) throw new ArgumentNullException(nameof(selector)); return selector.Match( f1 => source.Match( f2 => Fail<F, S>(combine(f1, f2)), _ => Fail<F, S>(f1)), map => source.Match( f2 => Fail<F, S>(f2), x => Succeed<F, S>(map(x)))); } public static Validated<F, Func<T2, S>> Apply<F, T1, T2, S>( this Validated<F, Func<T1, T2, S>> selector, Validated<F, T1> source, Func<F, F, F> combine) { if (selector is null) throw new ArgumentNullException(nameof(selector)); return selector.Match( f1 => source.Match( f2 => Fail<F, Func<T2, S>>(combine(f1, f2)), _ => Fail<F, Func<T2, S>>(f1)), map => source.Match( f2 => Fail<F, Func<T2, S>>(f2), x => Succeed<F, Func<T2, S>>(y => map(x, y)))); } public static Validated<F, Func<T2, T3, S>> Apply<F, T1, T2, T3, S>( this Validated<F, Func<T1, T2, T3, S>> selector, Validated<F, T1> source, Func<F, F, F> combine) { if (selector is null) throw new ArgumentNullException(nameof(selector)); return selector.Match( f1 => source.Match( f2 => Fail<F, Func<T2, T3, S>>(combine(f1, f2)), _ => Fail<F, Func<T2, T3, S>>(f1)), map => source.Match( f2 => Fail<F, Func<T2, T3, S>>(f2), x => Succeed<F, Func<T2, T3, S>>((y, z) => map(x, y, z)))); } public static Validated<F, Func<T2, T3, S>> Apply<F, T1, T2, T3, S>( this Func<T1, T2, T3, S> map, Validated<F, T1> source, Func<F, F, F> combine) { return Apply( Succeed<F, Func<T1, T2, T3, S>>((x, y, z) => map(x, y, z)), source, combine); } }
I only added the Apply overloads that I needed for the following demo code. As stated above, I'm not going to launch into a detailed walk-through, since the code follows the concepts lined out in the various articles I've already mentioned. If there's something that you'd like me to explain then please leave a comment.
Notice that Validated<F, S> has no SelectMany method. It's deliberately not a monad, because monadic bind (SelectMany) would conflict with the applicative functor implementation.
Individual parsers #
An essential quality of applicative validation is that it's composable. This means that you can compose a larger, more complex parser from smaller ones. Parsing a ReservationDto object, for example, involves parsing the date and time of the reservation, the email address, and the quantity. Here's how to parse the date and time:
private Validated<string, DateTime> TryParseAt() { if (!DateTime.TryParse(At, out var d)) return Validated.Fail<string, DateTime>($"Invalid date or time: {At}."); return Validated.Succeed<string, DateTime>(d); }
In order to keep things simple I'm going to use strings for error messages. You could instead decide to encode error conditions as a sum type or other polymorphic type. This would be appropriate if you also need to be able to make programmatic decisions based on individual error conditions, or if you need to translate the error messages to more than one language.
The TryParseAt function only attempts to parse the At property to a DateTime value. If parsing fails, it returns a Failure value with a helpful error message; otherwise, it wraps the parsed date and time in a Success value.
Parsing the email address is similar:
private Validated<string, Email> TryParseEmail() { if (Email is null) return Validated.Fail<string, Email>($"Email address is missing."); return Validated.Succeed<string, Email>(new Email(Email)); }
As is parsing the quantity:
private Validated<string, int> TryParseQuantity() { if (Quantity < 1) return Validated.Fail<string, int>( $"Quantity must be a positive integer, but was: {Quantity}."); return Validated.Succeed<string, int>(Quantity); }
There's no reason to create a parser for the reservation name, because if the name doesn't exist, instead use the empty string. That operation can't fail.
Composition #
You can now use applicative composition to reuse those individual parsers in a more complex parser:
internal Validated<string, Reservation> TryParse(Guid id) { Func<DateTime, Email, int, Reservation> createReservation = (at, email, quantity) => new Reservation(id, at, email, new Name(Name ?? ""), quantity); Func<string, string, string> combine = (x, y) => string.Join(Environment.NewLine, x, y); return createReservation .Apply(TryParseAt(), combine) .Apply(TryParseEmail(), combine) .Apply(TryParseQuantity(), combine); }
createReservation is a local function that closes over id and Name. Specifically, it uses the null coalescing operator (??) to turn a null name into the empty string. On the other hand, it takes at, email, and quantity as inputs, since these are the values that must first be parsed.
A type like Validated<F, S> is only an applicative functor when the failure dimension (F) gives rise to a semigroup. The way I've modelled it here is as a binary operation that you need to pass as a parameter to each Apply overload. This seems awkward, but is good enough for a proof of concept.
The combine function joins two strings together, separated by a line break.
The TryParse function composes createReservation with TryParseAt, TryParseEmail, and TryParseQuantity using the various Apply overloads. The combination is a Validated value that's either a failure string or a properly encapsulated Reservation object.
One thing that I still don't like about this function is that it takes an id parameter. For an article about why that is a problem, and what to do about it, see Coalescing DTOs.
Using the parser #
Client code can now invoke the TryParse function on the DTO. Here is the code inside the Post method on the ReservationsController class:
[HttpPost("restaurants/{restaurantId}/reservations")] public Task<ActionResult> Post(int restaurantId, ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); var id = dto.ParseId() ?? Guid.NewGuid(); var parseResult = dto.TryParse(id); return parseResult.Match( msgs => Task.FromResult<ActionResult>(new BadRequestObjectResult(msgs)), reservation => TryCreate(restaurantId, reservation)); }
When the parseResult matches a failure, it returns a new BadRequestObjectResult with all collected error messages. When, on the other hand, it matches a success, it invokes the TryCreate helper method with the parsed reservation.
HTTP request and response #
A client will now receive all relevant error messages if it posts a malformed reservation:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
Content-Type: application/json
{ "at": "large", "name": "Kerry Onn", "quantity": -1 }
HTTP/1.1 400 Bad Request
Invalid date or time: large.
Email address is missing.
Quantity must be a positive integer, but was: -1.
Of course, if only a single element is wrong, only that error message will appear.
Conclusion #
The changes described in this article were entirely local to the two involved types: ReservationsController and ReservationDto. Once I'd expanded ReservationDto with the TryParse function and its helper functions, and changed ReservationsController accordingly, the rest of the code base compiled and all tests passed. The point is that this isn't a big change, and that's why I believe that the original design (returning null or non-null) doesn't invalidate anything else I had to say in the book.
The change did, however, take quite a bit of boilerplate code, as witnessed by the Validated code dump. That API is, on the other hand, completely reusable, and you can find packages on the internet that already implement this functionality. It's not much of a burden in terms of extra code, but it would have taken a couple of extra chapters to explain in the book. It could easily have been double the size if I had to include material about functors, applicative functors, semigroups, Church encoding, etcetera.
To fix two lines of code, I didn't think that was warranted. After all, it's not a major blocker. On the contrary, validation is a solved problem.
Comments
you can find packages on the internet that already implement this functionality
Do you have any recommendations for a library that implements the Validated<F, S> type?
Dan, thank you for writing. The following is not a recommendation, but the most comprehensive C# library for functional programming currently seems to be LanguageExt, which includes a Validation functor.
I'm neither recommending nor arguing against LanguageExt.
- I've never used it in a real-world code base.
- I've been answering questions about it on Stack Overflow. In general, it seems to stump C# developers, since it's very Haskellish and quite advanced.
- Today is just a point in time. Libraries come and go.
Since all the ideas presented in these articles are universal abstractions, you can safely and easily implement them yourself, instead of taking a dependency on a third-party library. If you stick with lawful implementations, the only variation possible is with naming. Do you call a functor like this one Validation, Validated, or something else? Do you call monadic bind SelectMany or Bind? Will you have a Flatten or a Join function?
When working with teams that are new to these things, I usually start by adding these concepts as source code as they become useful. If a type like Maybe or Validated starts to proliferate, sooner or later you'll need to move it to a shared library so that multiple in-house libraries can use the type to communicate results across library boundaries. Eventually, you may decide to move such a dependency to a NuGet package. You can, at such time, decide to use an existing library instead of your own.
The maintenance burden for these kinds of libraries is low, since the APIs and behaviour are defined and locked in advance by mathematics.
If you stick with lawful implementations, the only variation possible is with naming.
There are also language-specific choices that can vary.
One example involves applicative functors in C#. The "standard" API for applicative functors works well in Haskell and F# because it is designed to be used with curried functions, and both of those languages curry their functions by default. In contrast, applicative functors push the limits of what you can express in C#. I am impressed with the design that Language Ext uses for applicative functors, which is an extension method on a (value) tuple of applicative functor instances that accepts a lambda expression that is given all the "unwrapped" values "inside" the applicative functors.
Another example involves monads in TypeScript. To avoid the Pyramid of doom when performing a sequence of monadic operations, Haskell has do notation and F# has computation expressions. There is no equivalent language feature in TypeScript, but it has row polymorphism, which pf-ts uses to effectively implement do notation.
A related dimension is how to approximate high-kinded types in a language that lacks them. Language Ext passes in the monad as a type parameter as well as the "lower-kinded" type parameter and then constrains the monad type parameter to implement a monad interface parametereized by the lower type parameter as well as being a struct. I find that second constraint very intersting. Since the type parameter has a struct constraint, it has a default constructor that can be used to get an instance, which then implements methods according to the interface constraint. For more infomration, see this wiki article for a gentle introduction and Trans.cs for how Language Ext uses this approach to only implement traverse once. Similarly, F#+ has a feature called generic functions that enable one to write F# like map aFoo instead of the typical Foo.map aFoo.
Tyson, thank you for writing. I agree that details differ. Clearly, this is true across languages, where, say, Haskell's fmap has a name different from C#'s SelectMany. To state the obvious, the syntax is also different.
Even within the same language, you can have variations. Functor mapping in Haskell is generally called fmap, but you can also use map explicitly for lists. The same could be true in C#. I've seen functor and monad implementations in C# that use method names like Map and Bind rather than Select and SelectMany.
To expand on this idea, one may also observe that what one language calls Option, another language calls Maybe. The same goes for Result versus Either.
As you know, the names Select and SelectMany are special because they enable C# query syntax. While methods named Map and Bind are 'the same' functions, they don't light up that language feature. Another way to enable syntactic sugar for monads in C# is via async and await, as shown by Eirik Tsarpalis and Nick Palladinos.
I do agree with you that there are various options available to an implementer. The point I was trying to make is that while implementation details differ, the concepts are the same. Thus, as a user of one of these APIs (monads, monoids, etc.) you only have to learn the mental model once. You still have to learn the implementation details.
I recently heard a professor at DIKU state that once you know one programming language, you should be able to learn another one in a week. That's the same general idea.
(I do, however, have issues with that statement about programming languages as a universal assertion, but I agree that it tends to hold for mainstream languages. When I read Mazes for Programmers I'd never programmed in Ruby before, but I had little trouble picking it up for the exercises. On the other hand, most people don't learn Haskell in a week.)
Natural transformations
Mappings between functors, with some examples in C#.
This article is part of a series of articles about functor relationships. In this one you'll learn about natural transformations, which are simply mappings between two functors. It's probably the easiest relationship to understand. In fact, it may be so obvious that your reaction is: Is that it?
In programming, a natural transformation is just a function from one functor to another. A common example is a function that tries to extract a value from a collection. You'll see specific examples a little later in this article.
Laws #
In this, the dreaded section on laws, I have a nice surprise for you: There aren't any (that we need worry about)!
In the broader context of category theory there are, in fact, rules that a natural transformation must follow.
"Haskell's parametric polymorphism has an unexpected consequence: any polymorphic function of the type:
alpha :: F a -> G a"where
FandGare functors, automatically satisfies the naturality condition."
While C# isn't Haskell, .NET generics are similar enough to Haskell parametric polymorphism that the result, as far as I can tell, carry over. (Again, however, we have to keep in mind that C# doesn't distinguish between pure functions and impure actions. The knowledge that I infer translates for pure functions. For impure actions, there are no guarantees.)
The C# equivalent of the above alpha function would be a method like this:
G<T> Alpha<T>(F<T> f)
where both F and G are functors.
Safe head #
Natural transformations easily occur in normal programming. You've probably written some yourself, without being aware of it. Here are some examples.
It's common to attempt to get the first element of a collection. Collections, however, may be empty, so this is not always possible. In Haskell, you'd model that as a function that takes a list as input and returns a Maybe as output:
Prelude Data.Maybe> :t listToMaybe listToMaybe :: [a] -> Maybe a Prelude Data.Maybe> listToMaybe [] Nothing Prelude Data.Maybe> listToMaybe [7] Just 7 Prelude Data.Maybe> listToMaybe [3,9] Just 3 Prelude Data.Maybe> listToMaybe [5,9,2,4,4] Just 5
In many tutorials such a function is often called safeHead, because it returns the head of a list (i.e. the first item) in a safe manner. It returns Nothing if the list is empty. In F# this function is called tryHead.
In C# you could write a similar function like this:
public static Maybe<T> TryFirst<T>(this IEnumerable<T> source) { if (source.Any()) return new Maybe<T>(source.First()); else return Maybe.Empty<T>(); }
This extension method (which is really a pure function) is a natural transformation between two functors. The source functor is the list functor and the destination is the Maybe functor.
Here are some unit tests that demonstrate how it works:
[Fact] public void TryFirstWhenEmpty() { Maybe<Guid> actual = Enumerable.Empty<Guid>().TryFirst(); Assert.Equal(Maybe.Empty<Guid>(), actual); } [Theory] [InlineData(new[] { "foo" }, "foo")] [InlineData(new[] { "bar", "baz" }, "bar")] [InlineData(new[] { "qux", "quux", "quuz", "corge", "corge" }, "qux")] public void TryFirstWhenNotEmpty(string[] arr, string expected) { Maybe<string> actual = arr.TryFirst(); Assert.Equal(new Maybe<string>(expected), actual); }
All these tests pass.
Safe index #
The above safe head natural transformation is just one example. Even for a particular combination of functors like List to Maybe many natural transformations may exist. For this particular combination, there are infinitely many natural transformations.
You can view the safe head example as a special case of a more general set of safe indexing. With a collection of values, you can attempt to retrieve the value at a particular index. Since a collection can contain an arbitrary number of elements, however, there's no guarantee that there's an element at the requested index.
In order to avoid exceptions, then, you can try to retrieve the value at an index, getting a Maybe value as a result.
The F# Seq module defines a function called tryItem. This function takes an index and a sequence (IEnumerable<T>) and returns an option (F#'s name for Maybe):
> Seq.tryItem 2 [2;5;3;5];; val it : int option = Some 3
The tryItem function itself is not a natural transformation, but because of currying, it's a function that returns a natural transformation. When you partially apply it with an index, it becomes a natural transformation: Seq.tryItem 3 is a natural transformation seq<'a> -> 'a option, as is Seq.tryItem 4, Seq.tryItem 5, and so on ad infinitum. Thus, there are infinitely many natural transformations from the List functor to the Maybe functor, and safe head is simply Seq.tryItem 0.
In C# you can use the various Func delegates to implement currying, but if you want something that looks a little more object-oriented, you could write code like this:
public sealed class Index { private readonly int index; public Index(int index) { this.index = index; } public Maybe<T> TryItem<T>(IEnumerable<T> values) { var candidate = values.Skip(index).Take(1); if (candidate.Any()) return new Maybe<T>(candidate.First()); else return Maybe.Empty<T>(); } }
This Index class captures an index value for potential use against any IEnumerable<T>. Thus, the TryItem method is a natural transformation from the List functor to the Maybe functor. Here are some examples:
[Theory] [InlineData(0, new string[0])] [InlineData(1, new[] { "bee" })] [InlineData(2, new[] { "nig", "fev" })] [InlineData(4, new[] { "sta", "ali" })] public void MissItem(int i, string[] xs) { var idx = new Index(i); Maybe<string> actual = idx.TryItem(xs); Assert.Equal(Maybe.Empty<string>(), actual); } [Theory] [InlineData(0, new[] { "foo" }, "foo")] [InlineData(1, new[] { "bar", "baz" }, "baz")] [InlineData(1, new[] { "qux", "quux", "quuz" }, "quux")] [InlineData(2, new[] { "corge", "grault", "fred", "garply" }, "fred")] public void FindItem(int i, string[] xs, string expected) { var idx = new Index(i); Maybe<string> actual = idx.TryItem(xs); Assert.Equal(new Maybe<string>(expected), actual); }
Since there are infinitely many integers, there are infinitely many such natural transformations. (This is strictly not true for the above code, since there's a finite number of 32-bit integers. Exercise: Is it possible to rewrite the above Index class to instead work with BigInteger?)
The Haskell natural-transformation package offers an even more explicit way to present the same example:
import Control.Natural tryItem :: (Eq a, Num a, Enum a) => a -> [] :~> Maybe tryItem i = NT $ lookup i . zip [0..]
You can view this tryItem function as a function that takes a number and returns a particular natural transformation. For example you can define a value called tryThird, which is a natural transformation from [] to Maybe:
λ tryThird = tryItem 2 λ :t tryThird tryThird :: [] :~> Maybe
Here are some usage examples:
λ tryThird # [] Nothing λ tryThird # [1] Nothing λ tryThird # [2,3] Nothing λ tryThird # [4,5,6] Just 6 λ tryThird # [7,8,9,10] Just 9
In all three languages (F#, C#, Haskell), safe head is really just a special case of safe index: Seq.tryItem 0 in F#, new Index(0) in C#, and tryItem 0 in Haskell.
Maybe to List #
You can also move in the opposite direction: From Maybe to List. In F#, I can't find a function that translates from option 'a to seq 'a (IEnumerable<T>), but there are both Option.toArray and Option.toList. I'll use Option.toList for a few examples:
> Option.toList (None : string option);; val it : string list = [] > Option.toList (Some "foo");; val it : string list = ["foo"]
Contrary to translating from List to Maybe, going the other way there aren't a lot of options: None translates to an empty list, and Some translates to a singleton list.
Using a Visitor-based Maybe in C#, you can implement the natural transformation like this:
public static IEnumerable<T> ToList<T>(this IMaybe<T> source) { return source.Accept(new ToListVisitor<T>()); } private class ToListVisitor<T> : IMaybeVisitor<T, IEnumerable<T>> { public IEnumerable<T> VisitNothing { get { return Enumerable.Empty<T>(); } } public IEnumerable<T> VisitJust(T just) { return new[] { just }; } }
Here are some examples:
[Fact] public void NothingToList() { IMaybe<double> maybe = new Nothing<double>(); IEnumerable<double> actual = maybe.ToList(); Assert.Empty(actual); } [Theory] [InlineData(-1)] [InlineData( 0)] [InlineData(15)] public void JustToList(double d) { IMaybe<double> maybe = new Just<double>(d); IEnumerable<double> actual = maybe.ToList(); Assert.Single(actual, d); }
In Haskell this natural transformation is called maybeToList - just when you think that Haskell names are always abstruse, you learn that some are very explicit and self-explanatory.
If we wanted, we could use the natural-transformation package to demonstrate that this is, indeed, a natural transformation:
λ :t NT maybeToList NT maybeToList :: Maybe :~> []
There would be little point in doing so, since we'd need to unwrap it again to use it. Using the function directly, on the other hand, looks like this:
λ maybeToList Nothing [] λ maybeToList $ Just 2 [2] λ maybeToList $ Just "fon" ["fon"]
A Nothing value is always translated to the empty list, and a Just value to a singleton list, exactly as in the other languages.
Exercise: Is this the only possible natural transformation from Maybe to List?
Maybe-Either relationships #
The Maybe functor is isomorphic to Either where the left (or error) dimension is unit. Here are the two natural transformations in F#:
module Option = // 'a option -> Result<'a,unit> let toResult = function | Some x -> Ok x | None -> Error () // Result<'a,unit> -> 'a option let ofResult = function | Ok x -> Some x | Error () -> None
In F#, Maybe is called option and Either is called Result. Be aware that the F# Result discriminated union puts the Error dimension to the right of the Ok, which is opposite of Either, where left is usually used for errors, and right for successes (because what is correct is right).
Here are some examples:
> Some "epi" |> Option.toResult;; val it : Result<string,unit> = Ok "epi" > Ok "epi" |> Option.ofResult;; val it : string option = Some "epi"
Notice that the natural transformation from Result to Option is only defined for Result values where the Error type is unit. You could also define a natural transformation from any Result to option:
// Result<'a,'b> -> 'a option let ignoreErrorValue = function | Ok x -> Some x | Error _ -> None
That's still a natural transformation, but no longer part of an isomorphism due to the loss of information:
> (Error "Catastrophic failure" |> ignoreErrorValue : int option);; val it : int option = None
Just like above, when examining the infinitely many natural transformations from List to Maybe, we can use the Haskell natural-transformation package to make this more explicit:
ignoreLeft :: Either b :~> Maybe ignoreLeft = NT $ either (const Nothing) Just
ignoreLeft is a natural transformation from the Either b functor to the Maybe functor.
Using a Visitor-based Either implementation (refactored from Church-encoded Either), you can implement an equivalent IgnoreLeft natural transformation in C#:
public static IMaybe<R> IgnoreLeft<L, R>(this IEither<L, R> source) { return source.Accept(new IgnoreLeftVisitor<L, R>()); } private class IgnoreLeftVisitor<L, R> : IEitherVisitor<L, R, IMaybe<R>> { public IMaybe<R> VisitLeft(L left) { return new Nothing<R>(); } public IMaybe<R> VisitRight(R right) { return new Just<R>(right); } }
Here are some examples:
[Theory] [InlineData("OMG!")] [InlineData("Catastrophic failure")] [InlineData("Important information!")] public void IgnoreLeftOfLeft(string msg) { IEither<string, int> e = new Left<string, int>(msg); IMaybe<int> actual = e.IgnoreLeft(); Assert.Equal(new Nothing<int>(), actual); } [Theory] [InlineData(0)] [InlineData(1)] [InlineData(2)] public void IgnoreLeftOfRight(int i) { IEither<string, int> e = new Right<string, int>(i); IMaybe<int> actual = e.IgnoreLeft(); Assert.Equal(new Just<int>(i), actual); }
I'm not insisting that this natural transformation is always useful, but I've occasionally found myself in situations were it came in handy.
Natural transformations to or from Identity #
Some natural transformations are a little less obvious. If you have a NotEmptyCollection<T> class as shown in my article Semigroups accumulate, you could consider the Head property a natural transformation. It translates a NotEmptyCollection<T> object to a T object.
This function also exists in Haskell, where it's simply called head.
The input type (NotEmptyCollection<T> in C#, NonEmpty a in Haskell) is a functor, but the return type is a 'naked' value. That doesn't look like a functor.
True, a naked value isn't a functor, but it's isomorphic to the Identity functor. In Haskell, you can make that relationship quite explicit:
headNT :: NonEmpty :~> Identity headNT = NT $ Identity . NonEmpty.head
While not particularly useful in itself, this demonstrates that it's possible to think of the head function as a natural transformation from NonEmpty to Identity.
Can you go the other way, too?
Yes, indeed. Consider monadic return. This is a function that takes a 'naked' value and wraps it in a particular monad (which is also, always, a functor). Again, you may consider the 'naked' value as isomorphic with the Identity functor, and thus return as a natural transformation:
returnNT :: Monad m => Identity :~> m returnNT = NT $ return . runIdentity
We might even consider if a function a -> a (in Haskell syntax) or Func<T, T> (in C# syntax) might actually be a natural transformation from Identity to Identity... (It is, but only one such function exists.)
Not all natural transformations are useful #
Are are all functor combinations possible as natural transformations? Can you take any two functors and define one or more natural transformations? I'm not sure, but it seems clear that even if it is so, not all natural transformations are useful.
Famously, for example, you can't get the value out of the IO functor. Thus, at first glance it seems impossible to define a natural transformation from IO to some other functor. After all, how would you implement a natural transformation from IO to, say, the Identity functor. That seems impossible.
On the other hand, this is possible:
public static IEnumerable<T> Collapse<T>(this IO<T> source) { yield break; }
That's a natural transformation from IO<T> to IEnumerable<T>. It's possible to ignore the input value and always return an empty sequence. This natural transformation collapses all values to a single return value.
You can repeat this exercise with the Haskell natural-transformation package:
collapse :: f :~> [] collapse = NT $ const []
This one collapses any container f to a List ([]), including IO:
λ collapse # (return 10 :: IO Integer) [] λ collapse # putStrLn "ploeh" []
Notice that in the second example, the IO action is putStrLn "ploeh", which ought to produce the side effect of writing to the console. This is effectively prevented - instead the collapse natural transformation simply produces the empty list as output.
You can define a similar natural transformation from any functor (including IO) to Maybe. Try it as an exercise, in either C#, Haskell, or another language. If you want a Haskell-specific exercise, also define a natural transformation of this type: Alternative g => f :~> g.
These natural transformations are possible, but hardly useful.
Conclusion #
A natural transformation is a function that translates one functor into another. Useful examples are safe or total collection indexing, including retrieving the first element from a collection. These natural transformations return a populated Maybe value if the element exists, and an empty Maybe value otherwise.
Other examples include translating Maybe values into Either values or Lists.
A natural transformation can easily involve loss of information. Even if you're able to retrieve the first element in a collection, the return value includes only that value, and not the rest of the collection.
A few natural transformations may be true isomorphisms, but in general, being able to go in both directions isn't required. In degenerate cases, a natural transformation may throw away all information and map to a general empty value like the empty List or an empty Maybe value.
Next: Functor products.
Functor relationships
Sometimes you need to use more than one functor together.
This article series is part of a larger series of articles about functors, applicatives, and other mappable containers. Particularly, you've seen examples of both functors and applicative functors.
There are situations where you can get by with a single functor. Many languages come with list comprehensions or other features to work with collections of values (C#, for instance, has language-integrated query, or: LINQ). The list functor (and monad) gives you a comprehensive API to manipulate multiple values. Likewise, you may write some parsing (or validation) that exclusively uses the Either functor.
At other times, however, you may find yourself having to juggle more than one functor at once. Perhaps you are working with Either values, but one existing API returns Maybe values instead. Or perhaps you need to deal with Either values, but you're already working within an asynchronous functor.
There are several standard ways you can combine or transform combinations of functors.
A partial catalogue #
The following relationships often come in handy - particularly those that top this list:
This list is hardly complete, and I may add to it in the future. Compared to some of the other subtopics of the larger articles series on universal abstractions, this catalogue is more heterogeneous. It collects various ways that functors can relate to each other, but uses disparate concepts and abstractions, rather than a single general idea (like a bifunctor, monoid, or catamorphism).
Keep in mind when reading these articles that all monads are also functors and applicative functors, so what applies to functors also applies to monads.
Conclusion #
You can use a single functor in isolation, or you can combine more than one. Most of the relationships described in this articles series work for all (lawful) functors, but traversals require applicative functors and functors that are 'foldable' (i.e. a catamorphism exists).
Next: Natural transformations.
Get and Put State
A pair of standard helper functions for the State monad. An article for object-oriented programmers.
The State monad is completely defined by its two defining functions (SelectMany and Return). While you can get by without them, two additional helper functions (get and put) are so convenient that they're typically included. To be clear, they're not part of the State monad - rather, you can consider them part of what we may term a standard State API.
In short, get is a function that, as the name implies, gets the state while inside the State monad, and put replaces the state with a new value.
Later in this article, I'll show how to implement these two functions, as well as a usage example. Before we get to that, however, I want to show a motivating example. In other words, an example that doesn't use get and put.
The code shown in this article uses the C# State implementation from the State monad article.
Aggregator #
Imagine that you have to implement a simple Aggregator.
"How do we combine the results of individual but related messages so that they can be processed as a whole?"
[...] "Use a stateful filter, an Aggregator, to collect and store individual messages until it receives a complete set of related messages. Then, the Aggregator publishes a single message distilled from the individual messages."
The example that I'll give here is simplified and mostly focuses on how to use the State monad to implement the desired behaviour. The book Enterprise Integration Patterns starts with a simple example where messages arrive with a correlation ID as an integer. The message payload is also a an integer, just to keep things simple. The Aggregator should only publish an aggregated message once it has received three correlated messages.
Using the State monad, you could implement an Aggregator like this:
public sealed class Aggregator : IState<IReadOnlyDictionary<int, IReadOnlyCollection<int>>, Maybe<Tuple<int, int, int>>> { private readonly int correlationId; private readonly int value; public Aggregator(int correlationId, int value) { this.correlationId = correlationId; this.value = value; } public Tuple<Maybe<Tuple<int, int, int>>, IReadOnlyDictionary<int, IReadOnlyCollection<int>>> Run( IReadOnlyDictionary<int, IReadOnlyCollection<int>> state) { if (state.TryGetValue(correlationId, out var coll)) { if (coll.Count == 2) { var retVal = Tuple.Create(coll.ElementAt(0), coll.ElementAt(1), value); var newState = state.Remove(correlationId); return Tuple.Create(retVal.ToMaybe(), newState); } else { var newColl = coll.Append(value); var newState = state.Replace(correlationId, newColl); return Tuple.Create(new Maybe<Tuple<int, int, int>>(), newState); } } else { var newColl = new[] { value }; var newState = state.Add(correlationId, newColl); return Tuple.Create(new Maybe<Tuple<int, int, int>>(), newState); } } }
The Aggregator class implements the IState<S, T> interface. The full generic type is something of a mouthful, though.
The state type (S) is IReadOnlyDictionary<int, IReadOnlyCollection<int>> - in other words, a dictionary of collections. Each entry in the dictionary is keyed by a correlation ID. Each value is a collection of messages that belong to that ID. Keep in mind that, in order to keep the example simple, each message is just a number (an int).
The value to produce (T) is Maybe<Tuple<int, int, int>>. This code example uses this implementation of the Maybe monad. The value produced may or may not be empty, depending on whether the Aggregator has received all three required messages in order to produce an aggregated message. Again, for simplicity, the aggregated message is just a triple (a three-tuple).
The Run method starts by querying the state dictionary for an entry that corresponds to the correlationId. This entry may or may not be present. If the message is the first in a series of three, there will be no entry, but if it's the second or third message, the entry will be present.
In that case, the Run method checks the Count of the collection. If the Count is 2, it means that two other messages with the same correlationId was already received. This means that the Aggregator is now handling the third and final message. Thus, it creates the retVal tuple, removes the entry from the dictionary to create the newState, and returns both.
If the state contains an entry for the correlationId, but the Count isn't 2, the Run method updates the entry by appending the value, updating the state to newState, and returns that together with an empty Maybe value.
Finally, if there is no entry for the correlationId, the Run method creates a new collection containing only the value, adds it to the state dictionary, and returns the newState together with an empty Maybe value.
Message handler #
A message handler could be a background service that receives messages from a durable queue, a REST endpoint, or based on some other technology.
After it receives a message, a message handler would create a new instance of the Aggregator:
var a = new Aggregator(msg.CorrelationId, msg.Value);
Since Aggregator implements the IState<S, T> interface, the object a represents a stateful computation. A message handler might keep the current state in memory, or rehydrate it from some persistent storage system. Keep in mind that the state must be of the type IReadOnlyDictionary<int, IReadOnlyCollection<int>>. Wherever it comes from, assume that this state is a variable called s (for state).
The message handler can now Run the stateful computation by supplying s:
var t = a.Run(s);
The result is a tuple where the first item is a Maybe value, and the second item is the new state.
The message handler can now publish the triple if the Maybe value is populated. In any case, it can update the 'current' state with the new state. That's a nice little impureim sandwich.
Notice how this design is different from a typical object-oriented solution. In object-oriented programming, you'd typically have an object than contains the state and then receives the run-time value as input to a method that might then mutate the state. Data with behaviour, as it's sometimes characterised.
The State-based computation turns such a design on its head. The computation closes over the run-time values, and the state is supplied as an argument to the Run method. This is an example of the shift of perspective often required to think functionally, rather than object-oriented. That's why it takes time learning Functional Programming (FP); it's not about syntax. It's a different way to think.
An object like the above a seems almost frivolous, since it's going to have a short lifetime. Calling code will create it only to call its Run method and then let it go out of scope to be garbage-collected.
Of course, in a language more attuned to FP like Haskell, it's a different story:
let h = handle (corrId msg) (val msg)
Instead of creating an object using a constructor, you only pass the message values to a function called handle. The return value h is a State value that an overall message handler can then later run with a state s:
let (m, ns) = runState h s
The return value is a tuple where m is the Maybe value that may or may not contain the aggregated message; ns is the new state.
Is this better? #
Is this approach to state mutation better than the default kind of state mutation possible with most languages (including C#)? Why make things so complicated?
There's more than one answer. First, in a language like Haskell, state mutation is in general not possible. While you can do state mutation with the IO container in Haskell, this sets you completely free. You don't want to be free, because with freedom comes innumerable ways to shoot yourself in the foot. Constraints liberate.
While the IO monad allows uncontrolled state mutation (together with all sorts of other impure actions), the State monad constrains itself and callers to only one type of apparent mutation. The type of the state being 'mutated' is visible in the type system, and that's the only type of value you can 'mutate' (in Haskell, that is).
The State monad uses the type system to clearly communicate what the type of state is. Given a language like Haskell, or otherwise given sufficient programming discipline, you can tell from an object's type exactly what to expect.
This also goes a long way to explain why monads are such an important concept in Functional Programming. When discussing FP, a common question is: How do you perform side effects? The answer, as may be already implied by this article, is that you use monads. The State monad for local state mutation, and the IO monad for 'global' side effects.
Get #
Clearly you can write an implementation of IState<S, T> like the above Aggregator class. Must we always write a class that implements the interface in order to work within the State monad?
Monads are all about composition. Usually, you can compose even complex behaviour from smaller building blocks. Just consider the list monad, which in C# is epitomised by the IEnumerable<T> interface. You can write quite complex logic using the building blocks of Where, Select, Aggregate, Zip, etcetera.
Likewise, we should expect that to be the case with the State monad, and it is so. The useful extra combinators are get and put.
The get function enables a composition to retrieve the current state. Given the IState<S, T> interface, you can implement it like this:
public static IState<S, S> Get<S>() { return new GetState<S>(); } private class GetState<S> : IState<S, S> { public Tuple<S, S> Run(S state) { return Tuple.Create(state, state); } }
The Get function represents a stateful computation that copies the state over to the 'value' dimension, so to speak. Notice that the return type is IState<S, S>. Copying the state over to the position of the T generic type means that it becomes accessible to the expressions that run inside of Select and SelectMany.
You'll see an example once I rewrite the above Aggregator to be entirely based on composition, but in order to do that, I also need the put function.
Put #
The put function enables you to write a new state value to the underlying state dimension. The implementation in the current code base looks like this:
public static IState<S, Unit> Put<S>(S s) { return new PutState<S>(s); } private class PutState<S> : IState<S, Unit> { private readonly S s; public PutState(S s) { this.s = s; } public Tuple<Unit, S> Run(S state) { return Tuple.Create(Unit.Default, s); } }
This implementation uses a Unit value to represent void. As usual, we have the problem in C-based languages that void isn't a value, but fortunately, unit is isomorphic to void.
Notice that the Run method ignores the current state and instead replaces it with the new state s.
Look, no classes! #
The Get and Put functions are enough that we can now rewrite the functionality currently locked up in the Aggregator class. Instead of having to define a new class for that purpose, it's possible to compose our way to the same functionality by writing a function:
public static IState<IReadOnlyDictionary<int, IReadOnlyCollection<int>>, Maybe<Tuple<int, int, int>>> Aggregate(int correlationId, int value) { return from state in State.Get<IReadOnlyDictionary<int, IReadOnlyCollection<int>>>() let mcoll = state.TryGetValue(correlationId) let retVal = from coll in mcoll.Where(c => c.Count == 2) select Tuple.Create(coll.ElementAt(0), coll.ElementAt(1), value) let newState = retVal .Select(_ => state.Remove(correlationId)) .GetValueOrFallback( state.Replace( correlationId, mcoll .Select(coll => coll.Append(value)) .GetValueOrFallback(new[] { value }))) from _ in State.Put(newState) select retVal; }
Okay, I admit that there's a hint of code golf over this. It's certainly not idiomatic C#. To be clear, I'm not endorsing this style of C#; I'm only showing it to explain the abstraction offered by the State monad. Adopt such code at your own peril.
The first observation to be made about this code example is that it's written entirely in query syntax. There's a good reason for that. Query syntax is syntactic sugar on top of SelectMany, so you could, conceivably, also write the above expression using method call syntax. However, in order to make early values available to later expressions, you'd have to pass a lot of tuples around. For example, the above expression makes repeated use of mcoll, so had you been using method call syntax instead of query syntax, you would have had to pass that value on to subsequent computations as one item in a tuple. Not impossible, but awkward. With query syntax, all values remain in scope so that you can refer to them later.
The expression starts by using Get to get the current state. The state variable is now available in the rest of the expression.
The state is a dictionary, so the next step is to query it for an entry that corresponds to the correlationId. I've used an overload of TryGetValue that returns a Maybe value, which also explains (I hope) the m prefix of mcoll.
Next, the expression filters mcoll and creates a triple if the coll has a Count of two. Notice that the nested query syntax expression (from...select) isn't running in the State monad, but rather in the Maybe monad. The result, retVal, is another Maybe value.
That takes care of the 'return value', but we also need to calculate the new state. This happens in a somewhat roundabout way. The reason that it's not more straightforward is that C# query syntax doesn't allow branching (apart from the ternary ?..: operator) and (this version of the language, at least) has weak pattern-matching abilities.
Instead, it uses retVal and mcoll as indicators of how to update the state. If retVal is populated, it means that the Aggregate computation will return a triple, in which case it must Remove the entry from the state dictionary. On the other hand, if that's not the case, it must update the entry. Again, there are two options. If mcoll was already populated, it should be updated by appending the value. If not, a new entry containing only the value should be added.
Finally, the expression uses Put to save the new state, after which it returns retVal.
While this is far from idiomatic C# code, the point is that you can compose your way to the desired behaviour. You don't have to write a new class. Not that this is necessarily an improvement in C#. I'm mostly stating this to highlight a difference in philosophy.
Of course, this is all much more elegant in Haskell, where the same functionality is as terse as this:
handle :: (Ord k, MonadState (Map k [a]) m) => k -> a -> m (Maybe (a, a, a)) handle correlationId value = do m <- get let (retVal, newState) = case Map.lookup correlationId m of Just [x, y] -> (Just (x, y, value), Map.delete correlationId m) Just _ -> (Nothing, Map.adjust (++ [value]) correlationId m) Nothing -> (Nothing, Map.insert correlationId [value] m) put newState return retVal
Notice that this implementation also makes use of get and put.
Modify #
The Get and Put functions are basic functions based on the State monad abstraction. These two functions, again, can be used to define some secondary helper functions, whereof Modify is one:
public static IState<S, Unit> Modify<S>(Func<S, S> modify) { return Get<S>().SelectMany(s => Put(modify(s))); }
It wasn't required for the above Aggregate function, but here's a basic unit test that demonstrates how it works:
[Fact] public void ModifyExample() { var x = State.Modify((int i) => i + 1); var actual = x.Run(1); Assert.Equal(2, actual.Item2); }
It can be useful if you need to perform an 'atomic' state modification. For a realistic Haskell example, you may want to refer to my article An example of state-based testing in Haskell.
Gets #
Another occasionally useful second-order helper function is Gets:
public static IState<S, T> Gets<S, T>(Func<S, T> selector) { return Get<S>().Select(selector); }
This function can be useful as a combinator if you need just a projection of the current state, instead of the whole state.
Here's another basic unit test as an example:
[Fact] public void GetsExample() { IState<string, int> x = State.Gets((string s) => s.Length); Tuple<int, string> actual = x.Run("bar"); Assert.Equal(Tuple.Create(3, "bar"), actual); }
While the above Aggregator example didn't require Modify or Gets, I wanted to include them here for completeness sake.
F# #
Most of the code shown in this article has been C#, with the occasional Haskell code. You can also implement the State monad, as well as the helper methods, in F#, where it'd feel more natural to dispense with interfaces and instead work directly with functions. To make things a little clearer, you may want to define a type alias:
type State<'a, 's> = ('s -> 'a * 's)
You can now define a State module that works directly with that kind of function:
module State = let run state (f : State<_, _>) = f state let lift x state = x, state let map f x state = let x', newState = run state x f x', newState let bind (f : 'a -> State<'b, 's>) (x : State<'a, 's>) state = let x', newState = run state x run newState (f x') let get state = state, state let put newState _ = (), newState let modify f = get |> map f |> bind put
This is code I originally wrote for a Code Review answer. You can go there to see all the details, as well as a motivating example.
I see that I never got around to add a gets function... I'll leave that as an exercise.
In C#, I've based the example on an interface (IState<S, T>), but it would also be possible to implement the State monad as extension methods on Func<S, Tuple<T, S>>. Try it! It might be another good exercise.
Conclusion #
The State monad usually comes with a few helper functions: get, put, modify, and gets. They can be useful as combinators you can use to compose a stateful combination from smaller building blocks, just like you can use LINQ to compose complex queries over data.
Test Double clocks
A short exploration of replacing the system clock with Test Doubles.
In a comment to my article Waiting to never happen, Laszlo asks:
"Why have you decided to make the date of the reservation relative to the SystemClock, and not the other way around? Would it be more deterministic to use a faked system clock instead?"
The short answer is that I hadn't thought of the alternative. Not in this context, at least.
It's a question worth exploring, which I will now proceed to do.
Why IClock? #
The article in question discusses a unit test, which ultimately arrives at this:
[Fact] public async Task ChangeDateToSoldOutDate() { var r1 = Some.Reservation.WithDate(DateTime.Now.AddDays(8).At(20, 15)); var r2 = r1 .WithId(Guid.NewGuid()) .TheDayAfter() .WithQuantity(10); var db = new FakeDatabase(); db.Grandfather.Add(r1); db.Grandfather.Add(r2); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var dto = r1.WithDate(r2.At).ToDto(); var actual = await sut.Put(r1.Id.ToString("N"), dto); var oRes = Assert.IsAssignableFrom<ObjectResult>(actual); Assert.Equal( StatusCodes.Status500InternalServerError, oRes.StatusCode); }
The keen reader may notice that the test passes a new SystemClock() to the sut. In case you're wondering what that is, here's the definition:
public sealed class SystemClock : IClock { public DateTime GetCurrentDateTime() { return DateTime.Now; } }
While it should be possible to extrapolate the IClock interface from this code snippet, here it is for the sake of completeness:
public interface IClock { DateTime GetCurrentDateTime(); }
Since such an interface exists, why not use it in unit tests?
That's possible, but I think it's worth highlighting what motivated this interface in the first place. If you're used to a certain style of test-driven development (TDD), you may think that interfaces exist in order to support TDD. They may. That's how I did TDD 15 years ago, but not how I do it today.
The motivation for the IClock interface is another. It's there because the system clock is a source of impurity, just like random number generators, database queries, and web service invocations. In order to support repeatable execution, it's useful to log the inputs and outputs of impure actions. This includes the system clock.
The IClock interface doesn't exist in order to support unit testing, but in order to enable logging via the Decorator pattern:
public sealed class LoggingClock : IClock { public LoggingClock(ILogger<LoggingClock> logger, IClock inner) { Logger = logger; Inner = inner; } public ILogger<LoggingClock> Logger { get; } public IClock Inner { get; } public DateTime GetCurrentDateTime() { var output = Inner.GetCurrentDateTime(); Logger.LogInformation( "{method}() => {output}", nameof(GetCurrentDateTime), output); return output; } }
All code in this article originates from the code base that accompanies Code That Fits in Your Head.
The web application is configured to decorate the SystemClock with the LoggingClock:
services.AddSingleton<IClock>(sp => { var logger = sp.GetService<ILogger<LoggingClock>>(); return new LoggingClock(logger, new SystemClock()); });
While the motivation for the IClock interface wasn't to support testing, now that it exists, would it be useful for unit testing as well?
A Stub clock #
As a first effort, we might try to add a Stub clock:
public sealed class ConstantClock : IClock { private readonly DateTime dateTime; public ConstantClock(DateTime dateTime) { this.dateTime = dateTime; } // This default value is more or less arbitrary. I chose it as the date // and time I wrote these lines of code, which also has the implication // that it was immediately a time in the past. The actual value is, // however, irrelevant. public readonly static IClock Default = new ConstantClock(new DateTime(2022, 6, 19, 9, 25, 0)); public DateTime GetCurrentDateTime() { return dateTime; } }
This implementation always returns the same date and time. I called it ConstantClock for that reason.
It's trivial to replace the SystemClock with a ConstantClock in the above test:
[Fact] public async Task ChangeDateToSoldOutDate() { var clock = ConstantClock.Default; var r1 = Some.Reservation.WithDate( clock.GetCurrentDateTime().AddDays(8).At(20, 15)); var r2 = r1 .WithId(Guid.NewGuid()) .TheDayAfter() .WithQuantity(10); var db = new FakeDatabase(); db.Grandfather.Add(r1); db.Grandfather.Add(r2); var sut = new ReservationsController( clock, new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var dto = r1.WithDate(r2.At).ToDto(); var actual = await sut.Put(r1.Id.ToString("N"), dto); var oRes = Assert.IsAssignableFrom<ObjectResult>(actual); Assert.Equal( StatusCodes.Status500InternalServerError, oRes.StatusCode); }
As you can see, however, it doesn't seem to be enabling any simplification of the test. It still needs to establish that r1 and r2 relates to each other as required by the test case, as well as establish that they are valid reservations in the future.
You may protest that this is straw man argument, and that it would make the test both simpler and more readable if it would, instead, use explicit, hard-coded values. That's a fair criticism, so I'll get back to that later.
Fragility #
Before examining the above criticism, there's something more fundamental that I want to get out of the way. I find a Stub clock icky.
It works in this case, but may lead to fragile tests. What happens, for example, if another programmer comes by and adds code like this to the System Under Test (SUT)?
var now = Clock.GetCurrentDateTime(); // Sabotage: while (Clock.GetCurrentDateTime() - now < TimeSpan.FromMilliseconds(1)) { }
As the comment suggests, in this case it's pure sabotage. I don't think that anyone would deliberately do something like this. This code snippet even sits in an asynchronous method, and in .NET 'everyone' knows that if you want to suspend execution in an asynchronous method, you should use Task.Delay. I rather intend this code snippet to indicate that keeping time constant, as ConstantClock does, can be fatal.
If someone comes by and attempts to implement any kind of time-sensitive logic based on an injected IClock, the consequences could be dire. With the above sabotage, for example, the test hangs forever.
When I originally refactored time-sensitive tests, it was because I didn't appreciate having such ticking bombs lying around. A ConstantClock isn't ticking (that's the problem), but it still seems like a booby trap.
Offset clock #
It seems intuitive that a clock that doesn't go isn't very useful. Perhaps we can address that problem by setting the clock back. Not just a few hours, but days or years:
public sealed class OffsetClock : IClock { private readonly TimeSpan offset; private OffsetClock(DateTime origin) { offset = DateTime.Now - origin; } public static IClock Start(DateTime at) { return new OffsetClock(at); } // This default value is more or less arbitrary. I just picked the same // date and time as ConstantClock (which see). public readonly static IClock Default = Start(at: new DateTime(2022, 6, 19, 9, 25, 0)); public DateTime GetCurrentDateTime() { return DateTime.Now - offset; } }
An OffsetClock object starts ticking as soon as it's created, but it ticks at the same pace as the system clock. Time still passes. Rather than a Stub, I think that this implementation qualifies as a Fake.
Using it in a test is as easy as using the ConstantClock:
[Fact] public async Task ChangeDateToSoldOutDate() { var clock = OffsetClock.Default; var r1 = Some.Reservation.WithDate( clock.GetCurrentDateTime().AddDays(8).At(20, 15)); var r2 = r1 .WithId(Guid.NewGuid()) .TheDayAfter() .WithQuantity(10); var db = new FakeDatabase(); db.Grandfather.Add(r1); db.Grandfather.Add(r2); var sut = new ReservationsController( clock, new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var dto = r1.WithDate(r2.At).ToDto(); var actual = await sut.Put(r1.Id.ToString("N"), dto); var oRes = Assert.IsAssignableFrom<ObjectResult>(actual); Assert.Equal( StatusCodes.Status500InternalServerError, oRes.StatusCode); }
The only change from the version that uses ConstantClock is the definition of the clock variable.
This test can withstand the above sabotage, because time still passes at normal pace.
Explicit dates #
Above, I promised to return to the criticism that the test is overly abstract. Now that it's possible to directly control time, perhaps it'd simplify the test if we could use hard-coded dates and times, instead of all that relative-time machinery:
[Fact] public async Task ChangeDateToSoldOutDate() { var r1 = Some.Reservation.WithDate( new DateTime(2022, 6, 27, 20, 15, 0)); var r2 = r1 .WithId(Guid.NewGuid()) .WithDate(new DateTime(2022, 6, 28, 20, 15, 0)) .WithQuantity(10); var db = new FakeDatabase(); db.Grandfather.Add(r1); db.Grandfather.Add(r2); var sut = new ReservationsController( OffsetClock.Start(at: new DateTime(2022, 6, 19, 13, 43, 0)), new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var dto = r1.WithDate(r2.At).ToDto(); var actual = await sut.Put(r1.Id.ToString("N"), dto); var oRes = Assert.IsAssignableFrom<ObjectResult>(actual); Assert.Equal( StatusCodes.Status500InternalServerError, oRes.StatusCode); }
Yeah, not really. This isn't worse, but neither is it better. It's the same size of code, and while the dates are now explicit (which, ostensibly, is better), the reader now has to deduce the relationship between the clock offset, r1, and r2. I'm not convinced that this is an improvement.
Determinism #
In the original comment, Laszlo asked if it would be more deterministic to use a Fake system clock instead. This seems to imply that using the system clock is nondeterministic. Granted, it is when not used with care.
On the other hand, when used as shown in the initial test, it's almost deterministic. What time-related circumstances would have to come around for the test to fail?
The important precondition is that both reservations are in the future. The test picks a date eight days in the future. How might that precondition fail?
The only failure condition I can think of is if test execution somehow gets suspended after r1 and r2 are initialised, but before calling sut.Put. If you run the test on a laptop and put it to sleep for more than eight days, you may be so extremely lucky (or unlucky, depending on how you look at it) that this turns out to be the case. When execution resumes, the reservations are now in the past, and sut.Put will fail because of that.
I'm not convinced that this is at all likely, and it's not a scenario that I'm inclined to take into account.
And in any case, the test variation that uses OffsetClock is as 'vulnerable' to that scenario as the SystemClock. The only Test Double not susceptible to such a scenario is ConstantClock, but as you have seen, this has more immediate problems.
Conclusion #
If you've read or seen a sufficient amount of time-travel science fiction, you know that it's not a good idea to try to change time. This also seems to be the case here. At least, I can see a few disadvantages to using Test Double clocks, but no clear advantages.
The above is, of course, only one example, but the concern of how to control the passing of time in unit testing isn't new to me. This is something that have been an issue on and off since I started with TDD in 2003. I keep coming back to the notion that the simplest solution is to use as many pure functions as possible, combined with a few impure actions that may require explicit use of dates and times relative to the system clock, as shown in previous articles.
Comments
I agree to most described in this post. However, I still find StubClock as my 'default' approach. I summarized the my reasons in this gist reply.
Yeah, not really. This isn't worse, but neither is it better. It's the same size of code, and while the dates are now explicit (which, ostensibly, is better), the reader now has to deduce the relationship between the clock offset,r1, andr2. I'm not convinced that this is an improvement.
I think, you overlook an important fact here: It depends™.
As Obi Wan taught us, the point of view is often quite important. In this case, yes it's true, the changed code is more explicit, from a certain point of view, because the dates are now explicit. But: in the previous version, the relationships were explicit, whereas they have been rendered implicit now. Which is better depends on the context, and in this context, I think the change is for the worse.
In this context, I think we care neither about the specific dates nor the relationship between both reservation dates.
All we care about is their relationship to the present and that they are different from each other.
With that in mind, I'd suggest to extend your Some container with more datetimes, in addition to Now,
like FutureDate and OtherFutureDate.
How those are constructed is generally of no relevance to the current test. After all, if we wanted to be 100% sure about every piece, we'd basically have re-write our entire runtime for each test case, which would just be madness. And yes, I'd just construct them based on the current system time.
Regarding the overall argument, I'll say that dealing with time issues is generally a pain, but most of the time, we don't really need to deal with what happens at specific times. In those rare cases, yes, it makes sense to fix the test's time, but I'd leave that as a rare exception. Partly because such tests tend to require some kind of wide-ranging mock that messes with a lot of things.
If we're talking about stuff like Y2k-proofing (if you're too young to remember, look it up, kids), it bears thinking about actually creating a whole test machine (virtual or physical) with an appropriate system time and just running your test suite on there. In times of docker, I'll bet that that will be less pain in many cases than adding time-fixing mock stuff.
If passage of time is important, that's another bag of pain right there, but I'd look into segregating that as much as possible from everything else. If, for example, you need things to happen after 100 minutes have passed, I'd prefer having a single time-based event system that all other code can subscribe to and be called back when the interesting time arrives. That way, I can test the consumers without actually travelling through time, while testing the timer service will be reduced to making sure that events are fired at the appropriate times. The latter could even happen on a persistent test machine that just keeps running, giving you insight on long-time behavior (just an idea, not a prescription 😉).
Thank you for writing. It's a good point that the two alternatives that I compare really only represent different perspectives. As one part becomes more explicit, the other becomes more implicit, and vice versa. I hadn't though of that, so thank you for pointing that out.
Perhaps, as you suggest, a better API might be in order. I'm sure this isn't my last round around that block. I don't, however, want to add Now, FutureDate, etc. to the Some API. This module contains a collection of representative values of various equivalence classes, and in order to ensure test repeatability, they should be immutable and deterministic. This rules out hiding a call to DateTime.Now behind such an API.
That doesn't, however, rule out other types of APIs. If you move to test data generators instead, it might make sense to define a 'future date' generator.
All that said, I agree that the best way to test time-sensitive code is to model it in such a way that it's deterministic. I've touched on this topic before, and most of the tests in the sample code base that accompanies Code That Fits in Your Head takes that approach.
The test discussed in this article, however, sits higher in the Test Pyramid, and for such Facade Tests, I'd like to exercise them in as realistic a context as possible. That's why I run them on the real system clock.
The State monad
Stateful computations as a monad. An example for object-oriented programmers.
This article is an instalment in an article series about monads. A previous article described the State functor. As is the case with many (but not all) functors, this one also forms a monad.
This article continues where the State functor article stopped. It uses the same code base.
SelectMany #
A monad must define either a bind or join function. In C#, monadic bind is called SelectMany. Given the IState<S, T> interface defined in the State functor article, you can implement SelectMany like this:
public static IState<S, T1> SelectMany<S, T, T1>( this IState<S, T> source, Func<T, IState<S, T1>> selector) { return new SelectManyState<S, T, T1>(source, selector); } private class SelectManyState<S, T, T1> : IState<S, T1> { private readonly IState<S, T> source; private readonly Func<T, IState<S, T1>> selector; public SelectManyState( IState<S, T> source, Func<T, IState<S, T1>> selector) { this.source = source; this.selector = selector; } public Tuple<T1, S> Run(S state) { Tuple<T, S> tuple = source.Run(state); IState<S, T1> projection = selector(tuple.Item1); return projection.Run(tuple.Item2); } }
As SelectMany implementations go, this is easily the most complex so far in this article series. While it looks complex, it really isn't. It's only complicated.
The three lines of code in the Run method does most of the work. The rest is essentially ceremony required because C# doesn't have language features like object expressions.
To be fair, part of the boilerplate is also caused by using an interface instead of functions. In F# you could get by with as little as this:
let bind (f : 'a -> State<'b, 's>) (x : State<'a, 's>) state = let x', newState = run state x run newState (f x')
I found an F# State implementation on my hard drive that turned out to originate from this Code Review answer. You can go there to see it in context.
The SelectMany method first runs the source with the supplied state. This produces a tuple with a value and a new state. The value is tuple.Item1, which has the type T. The method proceeds to use that value to call the selector, which produces a new State value. Finally, the method runs the projection with the new state (tuple.Item2).
Monadic bind becomes useful when you have more than one function that returns a monadic value. Consider a code snippet like this:
IState<int, string> s = new Switch("foo", "bar").SelectMany(txt => new VowelExpander(txt));
This uses the silly VowelExpander class from the State functor article, as well as this new frivolous State implementation:
public sealed class Switch : IState<int, string> { private readonly string option1; private readonly string option2; public Switch(string option1, string option2) { this.option1 = option1; this.option2 = option2; } public Tuple<string, int> Run(int state) { if (0 <= state) return Tuple.Create(option1, state); var newState = 0; return Tuple.Create(option2, newState); } }
Both Switch and VowelExpander are State objects. If SelectMany didn't flatten as it goes, composition would have resulted in a nested State value. You'll see an example later in this article.
Query syntax #
Monads also enable query syntax in C# (just like they enable other kinds of syntactic sugar in languages like F# and Haskell). As outlined in the monad introduction, however, you must add a special SelectMany overload:
public static IState<S, T1> SelectMany<S, T, U, T1>( this IState<S, T> source, Func<T, IState<S, U>> k, Func<T, U, T1> s) { return source.SelectMany(x => k(x).Select(y => s(x, y))); }
As already predicted in the monad introduction, this boilerplate overload is always implemented in the same way. Only the signature changes. With it, you could instead write the above composition of Switch and VowelExpander like this:
IState<int, string> s = from txt in new Switch("foo", "bar") from txt1 in new VowelExpander(txt) select txt1;
That example requires a new variable (txt1). Given that it's often difficult to come up with good variable names, this doesn't look like much of an improvement. Still, it's possible.
Join #
In the introduction you learned that if you have a Flatten or Join function, you can implement SelectMany, and the other way around. Since we've already defined SelectMany for IState<S, T>, we can use that to implement Join. In this article I use the name Join rather than Flatten. This is an arbitrary choice that doesn't impact behaviour. Perhaps you find it confusing that I'm inconsistent, but I do it in order to demonstrate that the behaviour is the same even if the name is different.
The concept of a monad is universal, but the names used to describe its components differ from language to language. What C# calls SelectMany, Scala calls flatMap, and what Haskell calls join, other languages may call Flatten.
You can always implement Join by using SelectMany with the identity function.
public static IState<S, T> Join<S, T>(this IState<S, IState<S, T>> source) { return source.SelectMany(x => x); }
Here's a way you can use it:
IState<int, IState<int, string>> nested = new Switch("foo", "bar").Select(txt => (IState<int, string>)new VowelExpander(txt)); IState<int, string> flattened = nested.Join();
Of the three examples involving Switch and VowelExpander, this one most clearly emphasises the idea that a monad is a functor you can flatten. Using Select (instead of SelectMany) creates a nested State value when you try to compose the two together. With Join you can flatten them.
Not that doing it this way is better in any way. In practice, you'll mostly use either SelectMany or query syntax. It's a rare case when I use something like Join.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. Conceptually, I call this function return (because that's the name that Haskell uses):
public static IState<S, T> Return<S, T>(T x) { return new ReturnState<S, T>(x); } private class ReturnState<S, T> : IState<S, T> { private readonly T x; public ReturnState(T x) { this.x = x; } public Tuple<T, S> Run(S state) { return Tuple.Create(x, state); } }
Like the above SelectMany implementation, this is easily the most complicated Return implementation so far shown in this article series. Again, however, most of it is just boilerplate necessitated by C#'s lack of certain language features (most notably object expressions). And again, this is also somewhat unfair because I could have chosen to demonstrate the State monad using Func<S, Tuple<T, S>> instead of an interface. (This would actually be a good exercise; try it!)
If you strip away all the boilerplate, the implementation is a trivial one-liner (the Run method), as also witnessed by this equivalent F# function that just returns a tuple:
let lift x state = x, state
When partially applied (State.lift x) that function returns a State value (i.e. a 's -> 'a * 's function).
Again, you can see that F# code in context in this Code Review answer.
Left identity #
We need to identify the return function in order to examine the monad laws. Now that this is done, let's see what the laws look like for the State monad, starting with the left identity law.
[Theory] [InlineData(DayOfWeek.Monday, 2)] [InlineData(DayOfWeek.Tuesday, 0)] [InlineData(DayOfWeek.Wednesday, 19)] [InlineData(DayOfWeek.Thursday, 42)] [InlineData(DayOfWeek.Friday, 2112)] [InlineData(DayOfWeek.Saturday, 90)] [InlineData(DayOfWeek.Sunday, 210)] public void LeftIdentity(DayOfWeek a, int state) { Func<DayOfWeek, IState<int, DayOfWeek>> @return = State.Return<int, DayOfWeek>; Func<DayOfWeek, IState<int, string>> h = dow => new VowelExpander(dow.ToString()); Assert.Equal(@return(a).SelectMany(h).Run(state), h(a).Run(state)); }
In order to compare the two State values, the test has to Run them and then compare the return values.
Right identity #
In a similar manner, we can showcase the right identity law as a test.
[Theory] [InlineData( true, 0)] [InlineData( true, 1)] [InlineData( true, 8)] [InlineData(false, 0)] [InlineData(false, 2)] [InlineData(false, 7)] public void RightIdentity(bool a, int state) { Func<bool, IState<int, string>> f = b => new VowelExpander(b.ToString()); Func<string, IState<int, string>> @return = State.Return<int, string>; IState<int, string> m = f(a); Assert.Equal(m.SelectMany(@return).Run(state), m.Run(state)); }
As always, even a parametrised test constitutes no proof that the law holds. I show the tests to illustrate what the laws look like in 'real' code.
Associativity #
The last monad law is the associativity law that describes how (at least) three functions compose. We're going to need three functions. For the purpose of demonstrating the law, any three pure functions will do. While the following functions are silly and not at all 'realistic', they have the virtue of being as simple as they can be (while still providing a bit of variety). They don't 'mean' anything, so don't worry too much about their behaviour. It is, as far as I can tell, nonsensical. Later articles will show some more realistic examples of the State monad in action.
private sealed class F : IState<DateTime, int> { private readonly string s; public F(string s) { this.s = s; } public Tuple<int, DateTime> Run(DateTime state) { var i = s.Length; var newState = state.AddDays(i); var newValue = i + state.Month; return Tuple.Create(newValue, newState); } } private sealed class G : IState<DateTime, TimeSpan> { private readonly int i; public G(int i) { this.i = i; } public Tuple<TimeSpan, DateTime> Run(DateTime state) { var newState = state.AddYears(i - state.Year); var newValue = TimeSpan.FromMinutes(i); return Tuple.Create(newValue, newState); } } public sealed class H : IState<DateTime, bool> { private readonly TimeSpan duration; public H(TimeSpan duration) { this.duration = duration; } public Tuple<bool, DateTime> Run(DateTime state) { var newState = state - duration; bool newValue = newState.DayOfWeek == DayOfWeek.Saturday || newState.DayOfWeek == DayOfWeek.Sunday; return Tuple.Create(newValue, newState); } }
Armed with these three classes, we can now demonstrate the Associativity law:
[Theory] [InlineData("foo", "2022-03-23")] [InlineData("bar", "2021-12-23T18:05")] [InlineData("baz", "1984-01-06T00:33")] public void Associativity(string a, DateTime state) { Func<string, IState<DateTime, int>> f = s => new F(s); Func<int, IState<DateTime, TimeSpan>> g = i => new G(i); Func<TimeSpan, IState<DateTime, bool>> h = ts => new H(ts); IState<DateTime, int> m = f(a); Assert.Equal( m.SelectMany(g).SelectMany(h).Run(state), m.SelectMany(x => g(x).SelectMany(h)).Run(state)); }
The version of xUnit.net I'm using for these examples (xUnit.net 2.2.0 on .NET Framework 4.6.1 - I may already have hinted that this is an old code base I had lying around) comes with a converter between string and DateTime, which explains why the [InlineData] can supply DateTime values as strings.
Conclusion #
For people coming from an imperative or object-oriented background, it can often be difficult to learn how to think 'functionally'. It took me years before I felt that I was on firm ground, and even so, I'm still learning new techniques today. As an imperative programmer, one often thinks in terms of state mutation.
In Functional Programming, there are often other ways to solve problems than in object-oriented programming, but if you can't think of a way, you can often reach for the fairly blunt hammer than the State monad is. It enables you to implement ostensibly state-based algorithms in a functional way.
This article was abstract, because I wanted to focus on the monad nature itself, rather than on practical applications. Future articles will provide more useful examples.
Next: The Reader monad.
Some thoughts on naming tests
What is the purpose of a test name?
Years ago I was participating in a coding event where we did katas. My pairing partner and I was doing silent ping pong. Ping-pong style pair programming is when one programmer writes a test and passes the keyboard to the partner, who writes enough code to pass the test. He or she then writes a new test and passes control back to the first person. In the silent variety, you're not allowed to talk. This is an exercise in communicating via code.
My partner wrote a test and I made it pass. After the exercise was over, we were allowed to talk to evaluate how it went, and my partner remarked that he'd been surprised that I'd implemented the opposite behaviour of what he'd intended. (It was something where there was a fork in the logic depending on a number being less than or greater to zero; I don't recall the exact details.)
We looked at the test that he had written, and sure enough: He'd named the test by clearly indicating one behaviour, but then he'd written an assertion that looked for the opposite behaviour.
I hadn't even noticed.
I didn't read the test name. I only considered the test body, because that's the executable specification.
How tests are named #
I've been thinking about test names ever since. What is the role of a test name?
In some languages, you write unit tests as methods or functions. That's how you do it in C#, Java, and many other languages:
[Theory] [InlineData("Home")] [InlineData("Calendar")] [InlineData("Reservations")] public void WithControllerHandlesSuffix(string name) { var sut = new UrlBuilder(); var actual = sut.WithController(name + "Controller"); var expected = sut.WithController(name); Assert.Equal(expected, actual); }
Usually, when we define new class methods, we've learned that naming is important. Truly, this applies to test methods, too?
Yet, other languages don't use class methods to define tests. The most common JavaScript frameworks don't, and neither does Haskell HUnit. Instead, tests are simply values with labels.
This hints at something that may be important.
The role of test names #
If tests aren't necessarily class methods, then what role do names play?
Usually, when considering method names, it's important to provide a descriptive name in order to help client developers. A client developer writing calling code must figure out which methods to call on an object. Good names help with that.
Automated tests, on the other hand, have no explicit callers. There's no client developer to communicate with. Instead, a test framework such as xUnit.net scans the public API of a test suite and automatically finds the test methods to execute.
The most prominent motivation for writing good method names doesn't apply here. We must reevaluate the role of test names, also keeping in mind that with some frameworks, in some languages, tests aren't even methods.
Mere anarchy is loosed upon the world #
The story that introduces this article has a point. When considering a test, I tend to go straight to the test body. I only read the test name if I find the test body unclear.
Does this mean that the test name is irrelevant? Should we simply number the tests: Test1, Test212, and so on?
That hardly seems like a good idea - not even to a person like me who considers the test name secondary to the test definition.
This begs the question, though: If Test42 isn't a good name, then what does a good test name look like?
Naming schemes #
Various people suggest naming schemes. In the .NET world many people like Roy Osherove's naming standard for unit tests: [UnitOfWork_StateUnderTest_ExpectedBehavior]. I find it too verbose to my tastes, but my point isn't to attack this particular naming scheme. In my Types + Properties = Software article series, I experimented with using a poor man's version of Given When Then:
[<Property>] let ``Given deuce when player wins then score is correct`` (winner : Player) = let actual : Score = scoreWhenDeuce winner let expected = Advantage winner expected =! actual
It was a worthwhile experiment, but I don't think I ever used that style again. After all, Given When Then is just another way of saying Arrange Act Assert, and I already organise my test code according to the AAA pattern.
These days, I don't follow any particular naming scheme, but I do keep a guiding principle in mind.
Information channel #
A test name, whether it's a method name or a label, is an opportunity to communicate with the reader of the code. You can communicate via code, via names, via comments, and so on. A test name is more like a mandatory comment than a normal method name.
Books like Clean Code make a compelling case that comments should be secondary to good names. The point isn't that all comments are bad, but that some are:
var z = x + y; // Add x and y
It's rarely a good idea to add a comment that describes what the code does. This should already be clear from the code itself.
A comment can still provide important information that code can't easily do. It may explain the purpose of the code. I try to take this into account when naming tests: Not repeat what the code does, but suggest a hint about its raison d'être.
I try to strike a balance between Test2112 and Given deuce when player wins then score is correct. I view the task of naming tests as equivalent to producing section headings in an article like this one. They offer a hint at the kind of information that might be available in the section (The role of test names, How tests are named, or Information channel), but sometimes they're more tongue-in-cheek than helpful (Mere anarchy is loosed upon the world). I tend to name tests with a similar degree of precision (or lack thereof): HomeReturnsJson, NoHackingOfUrlsAllowed, GetPreviousYear, etcetera.
These names, in isolation, hardly tell you what the tests are about. I'm okay with that, because I don't think that they have to.
What do you use test names for? #
I occasionally discuss this question with other people. It seems to me that it's one of the topics where Socratic questioning breaks down:
Them: How do you name tests?
Me: I try to strike a balance between information and not repeating myself.
Them: How do you like this particular naming scheme?
Me: It looks verbose to me. It seems to be repeating what's already in the test code.
Them: I like to read the test name to see what the test does.
Me: If the name and test code disagree, which one is right?
Them: The test name should follow the naming scheme.
Me: Why do you find that important?
Them: It's got... electrolytes.
Okay, I admit that I'm a being uncharitable, but the point that I'm after is that test names are different, yet most people seem to reflect little on this.
When do you read test names?
Personally, I rarely read or otherwise use test names. When I'm writing a test, I also write the name, but at that point I don't really need the name. Sometimes I start with a placeholder name (Foo), write the test, and change the name once I understand what the test does.
Once a test is written, ideally it should just be sitting there as a regression test. The less you touch it, the better you can trust it.
You may have hundreds or thousands of tests. When you run your test suite, you care about the outcome. Did it pass or fail? The outcome is the result of a Boolean and operation. The test suite only passes when all tests pass, but you don't have to look at each test result. The aggregate result is enough as long as the test suite passes.
You only need to look at a test when it fails. When this happens, most tools enable you to go straight to the failing test by clicking on it. (And if this isn't possible, I usually find it easier to navigate to the failing test either by line number or by copying the test name and navigating to it by pasting the name into my editor's navigation UI.) You don't really need the name to find a failing test. If the test was named Test1337 it would be as easy to find as if it was named Given deuce when player wins then score is correct.
Once I look at a failing test, I start by looking at the test code and comparing that to the assertion message.
Usually, when a test fails, it breaks for a reason. A code change caused the test to fail. Often, the offending change was one you did ten seconds earlier. Armed with an assertion message and the test code, I usually understand the problem right away.
In rare cases the test is one that I've never seen before, and I'm confused about its purpose. This is when I read the test name. At that point, I appreciate if the name is helpful.
Conclusion #
I'm puzzled that people are so passionate about test names. I consider them the least important part of a test. A name isn't irrelevant, but I find the test code more important. The code is an executable specification. It expresses the desired truth about a system.
Test code is code that has the same lifetime as the production code. It pays to structure it as well as the production code. If a test is well-written, you should be able to understand it without reading its name.
That's an ideal, and in reality we are fallible. Thus, providing a helpful name gives the reader a second chance to understand a test. The name shouldn't, however, be your first priority.
Comments
I often want run selected tests from the command line and thus use the test runner's abilty to filter all available tests. Where the set of tests I want to run is all the tests below some point in the heirarchy of tests I can filter by the common prefix, or the test class name.
But I also often find myself wanting to run a set of tests that meet some functional criteria, e.g Validation approval tests, or All the tests for a particular feature across all the levels of the code base. In this case if the tests follow a naming convention where such test attributes are included in the test name, either via the method or class name, then such test filtering is possible.
Mark, are you a Classicist or a Mockist? I'm going to go out on a limb here and say you're probably a classicist. Test code written in a classicist style probably conveys the intent well already. I think code written in a Mockist style may not convey the intent as well, hence the test name (or a comment) becomes more useful to convey that information.
There are (at least) two ways of using test names (as well as test module names, as suggested by Struan Judd) that we make extensive use of in the LinkedIn code base and which I have used in every code base I have ever written tests for:
-
To indicate the intent of the test. It is well and good to say that the assertions should convey the conditions, but often it is not clear why a condition is intended to hold. Test names (and descriptive strings on the assertions) can go a very long way, especially when working in a large and/or unfamiliar code base, to understand whether the assertion remains relevant, or how it is relevant.
Now, granted: it is quite possible for those to get out of date, much as comments do. However, just as good comments remain valuable even though there is a risk of stale comments, good test names can be valuable even though they can also become stale.
The key, for me, is exactly the same as good comments—and you could argue that comments therefore obviate the need for test names. If we only cared about tests from the POV of reading the code, I would actually agree! However, because we often read the tests as a suite of assertions presented in some other UI (a terminal, a web view, etc.), the names and assertion descriptions themselves serve as the explanation when reading.
-
To provide structure and organization to the test suite. This is the same point Struan Judd was getting at: having useful test names lets you filter down to relevant chunks of the suite easily. This is valuable even on a small code base (like the
MaybeandResultlibrary in TypeScript a friend and I maintain), but it becomes invaluable when you have tens of thousands of tests to filter or search through, as in the main LinkedIn app!For that reason, we (and the Ember.js community more broadly) make extensive use of QUnit's
module()hook to name the set of modules under test (module('Rendering | SomeComponent', function () { ... }ormodule('Unit | some-utility', function () { ... }) as well as namingtest()(test('returns `null` if condition X does not hold', function (assert) { ... }) and indeed providing descriptive strings forassert()calls. We might even nestmodule()calls to make it easy to see and filter from how our test UI presents things: Rendering | SomeComponent > someMethod > a test description.
Now, how that plays out varies library to library. The aforementioned TS library just names the test with a decent description of what is under test (here, for example) as well as grouping them sensibly with overarching descriptions, and never uses assertion descriptions because they wouldn’t add anything. A couple of the libraries I wrote internally at LinkedIn, by contrast, make extensive use of both. It is, as usual, a tool to be employed as, and only as, it is useful. But it is indeed quite useful sometimes!
Struan, thank you for writing. I can't say that I've given much thought to the need to run subsets of a test suite. You have a point, though, that if that's a requirement, you need something on which to filter.
Is the name the appropriate criterion for that, though? It sounds brittle to me, but I grant that it depends on which alternatives are available. In xUnit.net, for example, you can use the [Trait] attribute to annotate tests with arbitrary metadata. I think that NUnit has a similar feature, but there's no guarantee that every unit testing framework on any platform or language supports such a feature.
Whenever a framework supports such metadata-based filtering, I'd favour relying on that instead of naming conventions. Naming conventions are vulnerable to misspellings and other programmer errors. That may also be true of metadata-based categorisation, but hopefully to a lesser degree, as these might enable you to use ordinary language features to keep the categories DRY.
Using names also sounds restrictive to me. Doesn't this mean that you have to be able to predict your filtering requirements when you decide on a naming scheme?
What if, later, you find that you need to filter on a different dimension? With metadata annotations, you should be able to add a new category to the affected tests, but how will you do that with an established naming scheme?
Overall, though, the reason that I haven't given this much thought is that I've never had the need to filter tests in arbitrary ways. You must be doing something different from how I work with tests. Why do you need to filter tests?
Eddie, thank you for writing. I don't find the linked article illuminating if one hasn't already heard about the terms mockist and classicist. I rather prefer the terms interaction-based and state-based testing. In any case, I started out doing interaction-based testing, but have since moved away from that. Even when I mainly wrote interaction-based tests, though, I didn't like rigid naming schemes. I don't see how that makes much of a difference.
I agree that a test name is a fine opportunity to convey intent. Did that not come across in the article?
Chris, thank you for writing. As I also responded to Eddie Stanley, I agree that a test name is a fine opportunity to convey intent. Did that not come across in the article?
To your second point, I'll refer you to my answer to Struan Judd. I'm still curious to learn why you find it necessary to categorise and filter tests.

Comments
Hello Mark. I was just wondering, is it possible to use the type system to do the validation instead ?
What I mean is, for example, to make all the ReservationDto's field a type with validation in the constructor (like a class name, a class email, and so on). Normally, when the framework will build ReservationDto, it will try to construct the fields using the type constructor, and if there is an explicit error thrown during the construction, the framework will send us back the error with the provided message.
Plus, I think types like "email", "name" and "at" are reusable. And I feel like we have more possibilities for validation with that way of doing than with the validation attributes.
What do you think ?
Regards.
Maurice, thank you for writing. I started writing a reply, but it grew, so I'm going to turn it into a blog post. I'll post an update here once I've published it, but expect it to take a few weeks.
I've published the article: Can types replace validation?.