ploeh blog danish software design
Closing database connections during test teardown
How to close database connections to SQL Server during integration testing teardown.
Whenever I need to run integration tests that involve SQL Server, I have a standard approach that I've evolved since 2007. It involves
- setting up a SQL Server Express database before each test
- running the test
- tearing down the database
One problem with that approach is that SQL Server doesn't allow you to delete a database if it has existing connections.
Turn off connection pooling #
I usually solve the problem by turning off connection pooling. For an integration test suite, this is fine. I usually use integration testing to verify functionality - not performance.
Turning off connection pooling is easily done by setting the flag to false in the connection string:
Server=(LocalDB)\MSSQLLocalDB;Database=Booking;Integrated Security=true;Pooling=false
This means that when you get to the teardown phase of the test, you can issue a DDL statement to the master database:
IF EXISTS (SELECT name
FROM master.dbo.sysdatabases
WHERE name = N'Booking')
DROP DATABASE [Booking]
When connection pooling is turned off, no other connections are open when you attempt to do that, and the database (here named Booking) is deleted.
Forcibly close other connections #
Recently, however, I ran into a testing scenario where connection pooling had to be turned on. When you turn on connection pooling, however, the above DROP DATABASE statement fails because at least one connection from the pool is still connected to the database.
To solve that issue, I forcibly close other connections during teardown:
IF EXISTS (SELECT name
FROM master.dbo.sysdatabases
WHERE name = N'Booking')
BEGIN
-- This closes existing connections:
ALTER DATABASE [Booking]
SET SINGLE_USER WITH ROLLBACK IMMEDIATE
DROP DATABASE [Booking]
END
Surprisingly, turning on connection pooling like this makes the integration tests slower. I suppose it's because throwing other connections off the database involves a bit of negotiation between the server and the clients, and that takes some time.
While slower, it does enable you to run the integration tests with connection pooling turned on. When you need it, you need it.
Summary #
You can run integration tests against a SQL Server Express database. People do it in various ways, but I've found that setting up and tearing down a pristine database for each test case is a robust and maintainable solution to the problem.
SQL Server will not, however, allow you to delete a database if other connections exist. The easiest and fastest solution to that problem is to turn off connection pooling.
Sometimes, you can't do that, so instead, you can expand your database teardown script so that it closes existing connections before it deletes the database.
Implementation of the C# IO container
Implementation details of the C# IO container.
This article is part of an article series about the IO container in C#. In the previous articles, you've seen how a type like IO<T> can be used to distinguish between pure functions and impure actions.
The point of the article series is to illustrate the concept that Haskell uses to impose the functional interaction law at compile time. The implementation details really aren't important. Still, I believe that I know my readership well enough that a substantial fraction would be left unsatisfied if I didn't share the implementation details.
I consider this an appendix to the article series. It's not really what this is all about, but here it is, nonetheless.
Constructor #
Based on the public API already published, the constructor implementation hardly comes as a surprise.
private readonly Func<T> item; public IO(Func<T> item) { this.item = item; }
The IO<T> class is little more than a wrapper around a lazily evaluated function, with the restriction that while you can put a Func<T> object into an IO object, you can never get it out again. Thus, the item is a private class field instead of a public property.
SelectMany #
The SelectMany method is a little more tricky:
public IO<TResult> SelectMany<TResult>(Func<T, IO<TResult>> selector) { return new IO<TResult>(() => selector(item()).item()); }
To guarantee referential transparency, we don't want the method to trigger evaluation of the lazy value, so the selector has to run inside a new lazy computation. This produces a lazy IO value that the method then has to unwrap inside another lazy computation. Such a translation from Func<IO<TResult>> to a new IO object with a Func<TResult> inside it is reminiscent of what in Haskell is known as a traversal.
UnsafePerformIO #
Finally, the UnsafePerformIO method isn't part of the API, but as explained in the previous article, this is the special method that the hypothetical parallel-world framework calls on the IO<Unit> returned by Main methods.
internal T UnsafePerformIO() { return item(); }
Since only the framework is supposed to call this method, it's internal by design. The only thing it does is to force evaluation of the lazy item.
Conclusion #
Most of the implementation of IO<T> is straightforward, with the single exception of SelectMany, which has to jump through a few hoops to keep the behaviour lazy until it's activated.
Once more I want to point out that the purpose of this article series is to explain how a type system like Haskell's guarantees referential transparency. C# could do the same, but it'd require that all impure actions in all libraries in the entire .NET ecosystem were to return IO values. That's not going to happen, but something similar already has happened. Read on in the next article.
Comments
In your previous post, you said
Haskell is a lazily evaluated language. That's an important piece of the puzzle, so I've modelled theIO<T>example so that it only wrapsLazyvalues. That emulates Haskell's behaviour in C#.
After several days, I finally feel like I fully understand this.
The concept of lazy has serveral slightly different definitions depending on the context. Haskell is a lazily evaluated language in the sense that its evaluation strategy is call by need. In C#, both Lazy<T> and Func<T> are lazy in the sense that neither actually contains a T, but both could produce a T if asked to do so. The difference is the presence or absence of caching. I remember all this by saying that Lazy<T> is lazy with caching and Func<T> is lazy without caching. So Lazy<T> is to call by need as Func<T> is to call by name.
Therefore, Lazy<T> is the correct choice if we want to model or emulate the evaluation strategy of Haskell in C#. What about Haskell's IO<T>? Is it lazy with caching or lazy without caching? My guess was lazy without caching, but I finally installed the ghc Haskell compiler and compiled Haskell on my machine for the first time in order to test this. I think this example shows that Haskell's IO<T> is lazy without caching.
-- output: xx
main =
let io = putStr "x"
in do { io ; io }
I think this would be equivalent C# code in this parallel world that you have created.
// output: x
static IO<Unit> MainIO(string[] args) {
var io = Console.Write("x");
return from _1 in io
from _2 in io
select Unit.Instance;
}
What makes me think that I fully understand this now is that I think I see where you are going. I think you already knew all this and decided to model Haskell's IO<T> using Lazy<T> anyway because Task<T> is also lazy with caching just like Lazy<T>, and your next post will discuss using Task<T> as a surrogate for Haskell's IO<T>. I think you want your C# implementation of IO<T> to be more like C#'s Task<T> than Haskell's IO<T>.
Thank you for including such a gem for me to think about...and enough motivation to finally put Haskell on my machine!
Tyson, thank you for writing. You've almost turned my blog into a peer-reviewed journal, and you've just pointed out a major blunder of mine 👍
I think I was mislead by the name Lazy, my attention was elsewhere, and I completely forgot about the memoisation that both Lazy<T> and Task<T> employ. It does turn out to be problematic in this context. Take the following example:
static IO<Unit> Main(string[] args) { IO<DateTime> getTime = Clock.GetLocalTime(); return getTime.SelectMany(t1 => Console.WriteLine(t1.Ticks.ToString()).Select(u1 => { Thread.Sleep(2); return Unit.Instance; }).SelectMany(u2 => getTime).SelectMany(t2 => Console.WriteLine(t2.Ticks.ToString()))); }
Notice that this example reuses getTime twice. We'd like any IO<T> value to represent an impure computation, so evaluating it twice with a 2 millisecond delay in between ought to yield two different results.
Due to the memoisation built into Lazy<T>, the first value is reused. That's not the behaviour we'd like to see.
While this is a rather big error on my part, it's fortunately only of a technical nature (I think). As you imply, the correct implementation is to use Func<T> rather than Lazy<T>:
public sealed class IO<T> { private readonly Func<T> item; public IO(Func<T> item) { this.item = item; } public IO<TResult> SelectMany<TResult>(Func<T, IO<TResult>> selector) { return new IO<TResult>(() => selector(item()).item()); } internal T UnsafePerformIO() { return item(); } }
This addresses the above reuse bug. With this implementation, the above Main method prints two different values, even though it reuses getTime.
Haskell IO doesn't memoise values, so this Func-based implementation better emulates the Haskell behaviour, which is actually what I wanted to do all along.
This mistake of mine is potentially so confusing that I think that it's best if I go back and edit the other posts in this articles series. Before I do that, though, I'd like to get your feedback.
Does this look better to you, or do you see other problems with it?
Tyson, thank you for writing. You've almost turned my blog into a peer-reviewed journal, and you've just pointed out a major blunder of mine 👍
You're welcome. I am certainly a peer, and I benefit greatly from closly reviewing your posts. They always give me so much to think about. I am happy that we both benefit from this :)
While this is a rather big error on my part, it's fortunately only of a technical nature (I think). ...
Haskell
IOdoesn't memoise values, so thisFunc-based implementation better emulates the Haskell behaviour, which is actually what I wanted to do all along.This mistake of mine is potentially so confusing that I think that it's best if I go back and edit the other posts in this articles series. Before I do that, though, I'd like to get your feedback.
Does this look better to you, or do you see other problems with it?
Yes, your Func<T>-based implementation better emulates Haskell's IO<T>. My guess was that you had used Lazy<T> with its caching behavior in mind. I do think it is a minor issue. I can't think of any code that I would write on purpose that would depend on this difference.
I think editing the previous posts depends on exactly how you want to suggesst Task<T> as an IO<T> surrogate.
From a purely teaching perspective, I think I prefer to first implement Haskell's IO<T> in C# using Func<T>, then suggest this implemention is essentialy the same as Task<T>, then point out the caching difference for those that are still reading. It would be a shame to lose some readers eariler by pointing out the difference too soon. I wouldn't expect you lost any readres in your current presentation that includes the caching difference but without mentioning it.
Func<T>, Lazy<T>, and Task<T> are all lazy (in the sense that none contain a T but all could produce one if requested. Here are their differences:
Func<T>is synchronous without caching,Lazy<T>is synchronous with caching, andTask<T>is asynchronous with caching.
Func<T> and Task<T>. The nested type Func<Task<T>> can asynchronously produce a T without caching. Maybe this would be helpful in this article series.
Overall though, I don't know of any other potential changes to consider.
For any reader following the discussion after today (July 24, 2020), it may be slightly confusing. Based on Tyson Williams' feedback, I've edited the article series with the above implementation. The previous incarnation of the article series had this implementation of IO<T>:
public sealed class IO<T> { private readonly Lazy<T> item; public IO(Lazy<T> item) { this.item = item; } public IO<TResult> SelectMany<TResult>(Func<T, IO<TResult>> selector) { var res = new Lazy<IO<TResult>>(() => selector(item.Value)); return new IO<TResult>( new Lazy<TResult>(() => res.Value.item.Value)); } internal T UnsafePerformIO() { return item.Value; } }
As this discussion reveals, the memoisation performed by Lazy<T> causes problems. After thinking it through, I've decided to retroactively change the articles in the series. This is something that I rarely do, but in this case I think is the best way forward, as the Lazy-based implementation could be confusing to new readers.
Readers interested in the history of these articles can peruse the Git log.
Referential transparency of IO
How the IO container guarantees referential integrity. An article for object-oriented programmers.
This article is part of an article series about the IO container in C#. In a previous article you got a basic introduction to the IO<T> container I use to explain how a type system like Haskell's distinguishes between pure functions and impure actions.
The whole point of the IO container is to effectuate the functional interaction law: a pure function mustn't be able to invoke an impure activity. This rule follows from referential transparency.
The practical way to think about it is to consider the two rules of pure functions:
- Pure functions must be deterministic
- Pure functions may have no side effects
IO<T> imposes those rules.
Determinism #
Like in the previous articles in this series, you must imagine that you're living in a parallel universe where all impure library functions return IO<T> objects. By elimination, then, methods that return naked values must be pure functions.
Consider the Greet function from the previous article. Since it returns a plain string, you can infer that it must be a pure function. What prevents it from doing something impure?
What if you thought that passing now as an argument is a silly design. Couldn't you just call Clock.GetLocalTime from the method?
Well, yes, in fact you can:
public static string Greet(DateTime now, string name) { IO<DateTime> now1 = Clock.GetLocalTime(); var greeting = "Hello"; if (IsMorning(now)) greeting = "Good morning"; if (IsAfternoon(now)) greeting = "Good afternoon"; if (IsEvening(now)) greeting = "Good evening"; if (string.IsNullOrWhiteSpace(name)) return $"{greeting}."; return $"{greeting}, {name.Trim()}."; }
This compiles, but is only the first refactoring step you have in mind. Next, you want to extract the DateTime from now1 so that you can get rid of the now parameter. Alas, you now run into an insuperable barrier. How do you get the DateTime out of the IO?
You can't. By design.
While you can call the GetLocalTime method, you can't use the return value. The only way you can use it is by composing it with SelectMany, but that still accomplishes nothing unless you return the resulting IO object. If you do that, though, you've now turned the entire Greet method into an impure action.
You can't perform any non-deterministic behaviour inside a pure function.
Side effects #
How does IO<T> protect against side effects? In the Greet method, couldn't you just write to the console, like the following?
public static string Greet(DateTime now, string name) { Console.WriteLine("Side effect!"); var greeting = "Hello"; if (IsMorning(now)) greeting = "Good morning"; if (IsAfternoon(now)) greeting = "Good afternoon"; if (IsEvening(now)) greeting = "Good evening"; if (string.IsNullOrWhiteSpace(name)) return $"{greeting}."; return $"{greeting}, {name.Trim()}."; }
This also compiles, despite our best efforts. That's unfortunate, but, as you'll see in a moment, it doesn't violate referential transparency.
In Haskell or F# equivalent code would make the compiler complain. Those compilers don't have special knowledge about IO, but they can see that an action returns a value. F# generates a compiler warning if you ignore a return value. In Haskell the story is a bit different, but the result is the same. Those compilers complain because you try to ignore the return value.
You can get around the issue using the language's wildcard pattern. This tells the compiler that you're actively ignoring the result of the action. You can do the same in C#:
public static string Greet(DateTime now, string name) { IO<Unit> _ = Console.WriteLine("Side effect!"); var greeting = "Hello"; if (IsMorning(now)) greeting = "Good morning"; if (IsAfternoon(now)) greeting = "Good afternoon"; if (IsEvening(now)) greeting = "Good evening"; if (string.IsNullOrWhiteSpace(name)) return $"{greeting}."; return $"{greeting}, {name.Trim()}."; }
The situation is now similar to the above treatment of non-determinism. While there's no value of interest in an IO<Unit>, the fact that there's an object at all is a hint. Like Lazy<T>, that value isn't a result. It's a placeholder for a computation.
If there's a way to make the C# compiler complain about ignored return values, I'm not aware of it, so I don't know if we can get closer to how Haskell works than this. Regardless, keep in mind that I'm not trying to encourage you to write C# like this; I'm only trying to explain how Haskell enforces referential transparency at the type level.
Referential transparency #
While the above examples compile without warnings in C#, both are still referentially transparent!
This may surprise you. Particularly the second example that includes Console.WriteLine looks like it has a side effect, and thus violates referential transparency.
Keep in mind, though, what referential transparency means. It means that you can replace a particular function call with its value. For example, you should be able to replace the function call Greeter.Greet(new DateTime(2020, 6, 4, 12, 10, 0), "Nearth") with its return value "Hello, Nearth.", or the function call Greeter.Greet(new DateTime(2020, 6, 4, 7, 30, 0), "Bru") with "Good morning, Bru.", without changing the behaviour of the software. This property still holds.
Even when the Greet method includes the Console.WriteLine call, that side effect never happens.
The reason is that an IO object represents a potential computation that may take place (also known as a thunk). Notice that the IO<T> constructor takes a Func as argument. It's basically just a lazily evaluated function wrapped in such a way that you can't force evaluation.
Instead, you should imagine that after Main returns its IO<Unit> object, the parallel-universe .NET framework executes it.
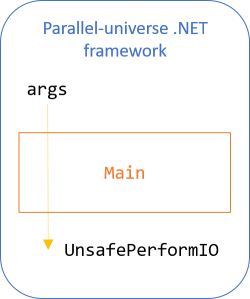
The framework supplies command-line arguments to the Main method. Once the method returns an IO<Unit> object, the framework executes it with a special method that only the framework can invoke. Any other IO values that may have been created (e.g. the above Console.WriteLine) never gets executed, because they're not included in the return value.
Conclusion #
The IO container makes sure that pure functions maintain referential transparency. The underlying assumption that makes all of this work is that all impure actions return IO objects. That's not how the .NET framework works, but that's how Haskell works. Since the IO container is opaque, pure functions can't see the contents of IO boxes.
Program entry points are all impure. The return value of the entry point must be IO<Unit>. The hypothetical parallel-universe framework executes the IO value returned by Main.
Haskell is a lazily evaluated language. That's an important piece of the puzzle, so I've modelled the IO<T> example so that it only wraps lazily evaluated Func values. That emulates Haskell's behaviour in C#. In the next article, you'll see how I wrote the C# code that supports these articles.
Comments
In a previous post, you said
...a pure function has to obey two rules:
- The same input always produces the same output.
- Calling it causes no side effects.
In this post, you said
...the two rules of pure functions:
- Pure functions must be deterministic
- Pure functions may have no side effects
The first two items are not the same. Is this difference intentional?
Tyson, thank you for writing. Indeed, the words er verbatim not the same, but I do intend them to carry the same meaning.
If one wants to define purity in a way that leaves little ambiguity, one has to use more words. Just look at the linked Wikipedia article. I link to Wikipedia for the benefit of those readers who'd like to get a more rigorous definition of the term, while at the same time I enumerate the two rules as a summary for the benefit of those readers who just need a reminder.
Does that answer your question?
...I do intend them to carry the same meaning.
I don't think they don't mean the same thing. That is part of the discussion we are having on this previous post. I think the simplest example to see the difference is randomzied quicksort. For each input, the output is always the same. However, randomized quicksort is not deterministic because it uses randomness.
Do you still think they mean the same thing?
You can get around the issue using the language's wildcard pattern. This tells the compiler that you're actively ignoring the result of the action.
You made a standard variable declaration and I believe you meant to use a stand-alone discard rather than a wildcard pattern? Like below?
public static string Greet(DateTime now, string name) { _ = Console.WriteLine("Side effect!"); var greeting = "Hello"; if (IsMorning(now)) greeting = "Good morning"; if (IsAfternoon(now)) greeting = "Good afternoon"; if (IsEvening(now)) greeting = "Good evening"; if (string.IsNullOrWhiteSpace(name)) return $"{greeting}."; return $"{greeting}, {name.Trim()}."; }
Tyson, I apologise in advance for my use of weasel words, but 'in the literature', a function that always returns the same output when given the same input is called 'deterministic'. I can't give you a comprehensive list of 'the literature' right now, but here's at least one example.
I'm well aware that this might be confusing. One could argue that querying a database is deterministic, because the output is completely determined by the state of the database. The same goes for reading the contents of a file. Such operations, however, may return different outputs for the same inputs, as the state of the resource changes. There's no stochastic process involved in such state changes, but we still consider such actions non-deterministic.
In the same vein, in this jargon, 'deterministic' doesn't imply the absence of internal randomness, as you have so convincingly argued. In the present context, 'deterministic' is defined as the property that a given input value always produces the same output value.
That's the reason I tend to use those phrases interchangeably. In this context, they literally mean the same. I can see how this might be confusing, though.
Atif, thank you for writing. I didn't know about that language construct. Thank you for pointing it out to me!
[Wikipedia says that] a function that always returns the same output when given the same input is called 'deterministic'.
In the same vein, in this jargon, 'deterministic' doesn't imply the absence of internal randomness, as you have so convincingly argued. In the present context, 'deterministic' is defined as the property that a given input value always produces the same output value.
That's the reason I tend to use those phrases interchangeably. In this context, they literally mean the same. I can see how this might be confusing, though.
I am certainly still confused. I can't tell if you are purposefully providing your own definition for determinism, if you are accidentally misunderstanding the actual definition of determinism, if you think the definition of determinism is equivalent to the definition you gave due to being in some context or operating with an additional assumption (of which I am unsure), or maybe something else.
If I had to guess, then I think you do see the difference between the two definitions but are claiming that are equivalent due to being in some context or operating with an additional assumption. If this guess is correct, then what is the additional assumption you are making?
To ensure that you do understand determinism, I will interpret your statements as literally as possible and then respond to them. I apologize in advance if this is not the correct interpretation and for any harshness in the tone of my response.
You misquoted the Wikipedia article. Here is the exact text (after replacing "algorithm" with "function" since the difference between these is not important to us now).
a deterministic function is a function which, given a particular input, will always produce the same output, with the underlying machine always passing through the same sequence of states.
Your quotation essentially excludes the phrase "with the underlying machine always passing through the same sequence of states". Let's put these two definitions next to each other.
Let f be a function. Consider the following two statements about f that might or might not be true (depending on the exact value of f).
- Given a particular input,
fwill always produce the same output. - Given a particular input,
fwill always produce the same output, with the underlying machine always passing through the same sequence of states.
Suppose some f satisfies statement 2. Then f clearly satisfies statement 1 as well. These two sentences together are equivalent to saying that statement 2 implies statement 1. The contrapositive then says that not satisfying statement 1 implies not satisfying statement 2. Also, Wikipedia says that such an f is said to be deterministic.
Now suppose some f satisfies statement 1. Then f need not also satisfy statement 2. An example that proves this is randomized quicksort (as I pointed out in this comment). This means that statement 1 does not imply statement 2.
"Wikipedia gave" a name to functions that satisfy statement 2. I do not recall ever seeing anyone give a name to functions that satisfy statement 1. In this comment, you asked me about what I meant by "weak determinism". I am trying to give a name to functions that satisfy statement 1. I am suggesting that we call them weakly deterministic. This name allows us to say that a deterministic function is also weakly deterministic, but a weakly deterministic function might not be deterministic. Furthermore, not being a weakly deterministic implies not being deterministic.
One could argue that querying a database is deterministic, because the output is completely determined by the state of the database. The same goes for reading the contents of a file. Such operations, however, may return different outputs for the same inputs, as the state of the resource changes. There's no stochastic process involved in such state changes, but we still consider such actions non-deterministic.
Indeed. I agree. If we distinguish determinism from weak determinism, then we can say that such a function is not weakly deterministic, which implies that it is not deterministic.
Tyson, I'm sorry, I picked a bad example. It's possible that my brain is playing a trick with me. I'm not purposefully providing my own definition of determinism.
I've learned all of this from diverse sources, and I don't recall all of them. Some of them are books, some were conference talks I attended, some may have been conversations, and some online resources. All of that becomes an amalgam of knowledge. Somewhere I've picked up the shorthand that 'deterministic' is the same as 'the same input produces the same output'; I can't tell you the exact source of that habit, and it may, indeed, be confusing.
It seems that I'm not the only person with that habit, though:
I'm not saying that John A De Goes is an authority you should unquestionably accept; I'm only pointing to that tweet to illustrate that I'm not the only person who occasionally use 'deterministic' in that way. And I don't think that John A De Goes picked up the habit from me."Deterministic: They return the same output for the same input."
The key to all of this is referential transparency. In an ideal world, I wouldn't need to use the terms 'pure function' or 'deterministic'. I can't, however, write these articles and only refer to referential transparency. The articles are my attempt to share what I have learned with readers who would also like to learn. The problem with referential transparency is that it's an abstract concept: can I replace a function call with its output? This may be a tractable notion to pick up, but how do you evaluate that in practice?
I believe that it's easier for readers to learn that they have to look for two properties:
- Does the same input always produce the same output?
- Are there no side effects?
As all programmers know: language is imprecise. Even the above two bullets are vague. What's a side effect? Does the rule about input and output apply to all values in the function's domain?
I don't think that it's possible to write perfectly precise and unambiguous prose. Mathematical notation was developed as an attempt to be more precise and unambiguous. Source code has the same quality.
I'm not writing mathematical treatises, but I use C#, F#, and Haskell source code to demonstrate concepts as precisely as I can. The surrounding prose is my attempt at explaining what the code does, and why it's written the way it is. The prose will be ambiguous; I can't help it.
Sometimes, I need a shorthand to remind the reader about referential transparency in a way that (hopefully) assists him or her. Sometimes, this is best done by using a few adjectives, such as "a deterministic and side-effect-free function". It's not a definition, it's a reading aid.
Mark, I am also sorry. As I reread my comment, I think I was too critical. I admire your great compassion and humility, especially in your writing. I have been trying to write more like you, but my previous comment shows that I still have room for improvement. Your blog is still my favorite place to read and learn about software development and functional programming. It is almost scary how much I agree with you. I hope posting questions about my confusion or comments about our differences don't overshadow all the ways in which we agree and sour our relationship.
Tyson, don't worry about it. Questions teach me where there's room for improvement. You also sometimes point out genuine mistakes that I make. If you didn't do that, I might never realise my mistakes, and then I wouldn't be able to correct them.
I appreciate the feedback because it improves the content and teaches me things that I didn't know. On the other hand, as the cliché goes, all errors are my own.
Syntactic sugar for IO
How to make use of the C# IO container less ugly.
This article is part of an article series about the IO container in C#. In the previous article you saw a basic C# hello world program using IO<T> to explicitly distinguish between pure functions and impure actions. The code wasn't as pretty as you could hope for. In this article, you'll see how to improve the aesthetics a bit.
The code isn't going to be perfect, but I think it'll be better.
Sugared version #
The IO<T> container is an imitation of the Haskell IO type. In Haskell, IO is a monad. This isn't a monad tutorial, and I hope that you're able to read the article without a deep understanding of monads. I only mention this because when you compose monadic values with each other, you'll sometimes have to write some 'noisy' code - even in Haskell. To alleviate that pain, Haskell offers syntactic sugar in the form of so-called do notation.
Likewise, F# comes with computation expressions, which also gives you syntactic sugar over monads.
C#, too, comes with syntactic sugar over monads. This is query syntax, but it's not as powerful as Haskell do notation or F# computation expressions. It's powerful enough, though, to enable you to improve the Main method from the previous article:
static IO<Unit> Main(string[] args) { return from _ in Console.WriteLine("What's your name?") from name in Console.ReadLine() from now in Clock.GetLocalTime() let greeting = Greeter.Greet(now, name) from res in Console.WriteLine(greeting) select res; }
If you use C# query syntax at all, you may think of it as exclusively the realm of object-relational mapping, but in fact it works for any monad. There's no data access going on here - just the interleaving of pure and impure code (in an impureim sandwich, even).
Infrastructure #
For the above code to compile, you must add a pair of methods to the IO<T> API. You can write them as extension methods if you like, but here I've written them as instance methods on IO<T>.
When you have multiple from keywords in the same query expression, you must supply a particular overload of SelectMany. This is an oddity of the implementation of the query syntax language feature in C#. You don't have to do anything similar to that in F# or Haskell.
public IO<TResult> SelectMany<U, TResult>(Func<T, IO<U>> k, Func<T, U, TResult> s) { return SelectMany(x => k(x).SelectMany(y => new IO<TResult>(() => s(x, y)))); }
Once you've implemented such overloads a couple of times, they're more tedious than challenging to write. They always follow the same template. First use SelectMany with k, and then SelectMany again with s. The only marginally stimulating part of the implementation is figuring out how to wrap the return value from s.
You're also going to need Select as shown in the article about IO as a functor.
Conclusion #
C#'s query syntax offers limited syntactic sugar over functors and monads. Compared with F# and Haskell, the syntax is odd and its functionality limited. The most galling lacuna is that you can't branch (e.g. use if or switch) inside query expressions.
The point of these articles is (still) not to endorse this style of programming. While the code I show in this article series is working C# code that runs and passes its tests, I'm pretending that all impure actions in C# return IO results. To be clear, the Console class this code interacts with isn't the Console class from the base class library. It's a class that pretends to be such a class from a parallel universe.
So far in these articles, you've seen how to compose impure actions with pure functions. What I haven't covered yet is the motivation for it all. We want the compiler to enforce the functional interaction law: a pure function shouldn't be able to invoke an impure action. That's the topic for the next article.
The IO functor
The IO container forms a functor. An article for object-oriented programmers.
This article is an instalment in an article series about functors. Previous articles have covered Maybe, Lazy, and other functors. This article provides another example.
Functor #
In a recent article, I gave an example of what IO might look like in C#. The IO<T> container already has sufficient API to make it a functor. All it needs is a Select method:
public IO<TResult> Select<TResult>(Func<T, TResult> selector) { return SelectMany(x => new IO<TResult>(() => selector(x))); }
This is an instance method on IO<T>, but you can also write it as an extension method, if that's more to your liking.
When you call selector(x), the return value is an object of the type TResult. The SelectMany method, however, wants you to return an object of the type IO<TResult>, so you use the IO constructor to wrap that return value.
Haskell #
The C# IO<T> container is an illustration of how Haskell's IO type works. It should come as no surprise to Haskellers that IO is a functor. In fact, it's a monad, and all monads are also functors.
The C# IO<T> API is based around a constructor and the SelectMany method. The constructor wraps a plain T value in IO<T>, so that corresponds to Haskell's return method. The SelectMany method corresponds to Haskell's monadic bind operator >>=. When you have lawful return and >>= implementations, you can have a Monad instance. When you have a Monad instance, you not only can have Functor and Applicative instances, you must have them.
Conclusion #
IO forms a functor, among other abstractions. In C#, this manifests as a proper implementation of a Select method.
Next: Monomorphic functors.
Comments
The constructor wraps a plainTvalue inIO<T>
Did you mean to say that the constructor wraps a Lazy<T> value in IO<T>?
Tyson, thank you for writing. Well, yes, that's technically what happens... I'm deliberately being imprecise with the language because I'm trying to draw a parallel to Haskell. In Haskell, return takes a value and wraps it in IO (the type is effectively a -> IO a). In Haskell, however, computation is lazy by default. This means that the value you wrap in IO is already lazy. This turns out to be important, as I'll explain in a future article, so in C# we have to first make sure that the value is lazy.
The concept, however, involves taking a 'bare' value and wrapping it in a container, and that's the reason I chose my words as I did.
IO container in a parallel C# universe
A C# model of IO at the type level.
This article is part of an article series about the IO container in C#. The previous article provided a conceptual overview. In this article you'll see C# code examples.
In a world... #
Imagine a parallel universe where a C# entry point is supposed to look like this:
static IO<Unit> Main(string[] args)
Like another Neo, you notice that something in your reality is odd, so you decide to follow the white rabbit. Unit? What's that? Navigating to its definition, you see this:
public sealed class Unit { public static readonly Unit Instance; }
There's not much to see here. Unit is a type that serves the same role as the void keyword. They're isomorphic, but Unit has the advantage that it's a proper type. This means that it can be a type parameter in a generically typed container like IO.
So what's IO? When you view its definition, this is what you see:
public sealed class IO<T> { public IO(Func<T> item) public IO<TResult> SelectMany<TResult>(Func<T, IO<TResult>> selector) }
There's a constructor you can initialise with a lazily evaluated value, and a SelectMany method that looks strikingly like something out of LINQ.
You'll probably notice right away that while you can put a value into the IO container, you can't get it back. As the introductory article explained, this is by design. Still, you may think: What's the point? Why would I ever want to use this class?
You get part of the answer when you try to implement your program's entry point. In order for it to compile, the Main method must return an IO<Unit> object. Thus, the simplest Main method that compiles is this:
static IO<Unit> Main(string[] args) { return new IO<Unit>(() => Unit.Instance); };
That's only a roundabout no-op. What if you want write real code? Like hello world?
Impure actions #
You'd like to write a program that asks the user about his or her name. Based on the answer, and the time of day, it'll write Hello, Nearth, or Good evening, Kate. You'd like to know how to take user input and write to the standard output stream. In this parallel world, the Console API looks like this:
public static class Console { public static IO<string> ReadLine(); public static IO<Unit> WriteLine(string value); // More members here... }
You notice that both methods return IO values. This immediately tells you that they're impure. This is hardly surprising, since ReadLine is non-deterministic and WriteLine has a side effect.
You'll also need the current time of day. How do you get that?
public static class Clock { public static IO<DateTime> GetLocalTime(); }
Again, IO signifies that the returned DateTime value is impure; it's non-deterministic.
Pure logic #
A major benefit of functional programming is the natural separation of concerns; separation of business logic from implementation details (a.k.a. the Dependency Inversion Principle).
Write the logic of the program as a pure function:
public static string Greet(DateTime now, string name) { var greeting = "Hello"; if (IsMorning(now)) greeting = "Good morning"; if (IsAfternoon(now)) greeting = "Good afternoon"; if (IsEvening(now)) greeting = "Good evening"; if (string.IsNullOrWhiteSpace(name)) return $"{greeting}."; return $"{greeting}, {name.Trim()}."; }
You can tell that this is a pure function from its return type. In this parallel universe, all impure library methods look like the above Console and Clock methods. Thus, by elimination, a method that doesn't return IO is pure.
Composition #
You have impure actions you can invoke, and a pure piece of logic. You can use ReadLine to get the user's name, and GetLocalTime to get the local time. When you have those two pieces of data, you can call the Greet method.
This is where most people run aground. "Yes, but Greet needs a string, but I have an IO<string>. How do I get the string out of the IO?
If you've been following the plot so far, you know the answer: mu. You don't. You compose all the things with SelectMany:
static IO<Unit> Main(string[] args) { return Console.WriteLine("What's your name?").SelectMany(_ => Console.ReadLine().SelectMany(name => Clock.GetLocalTime().SelectMany(now => { var greeting = Greeter.Greet(now, name); return Console.WriteLine(greeting); }))); }
I'm not going to walk through all the details of how this works. There's plenty of monad tutorials out there, but take a moment to contemplate the SelectMany method's selector argument. It takes a plain T value as input, but must return an IO<TResult> object. That's what each of the above lambda expressions do, but that means that name and now are unwrapped values; i.e. string and DateTime.
That means that you can call Greet with name and now, which is exactly what happens.
Notice that the above lambda expressions are nested. With idiomatic formatting, they'd exhibit the dreaded arrow shape, but with this formatting, it looks more like the sequential composition that it actually is.
Conclusion #
The code you've seen here all works. The only difference between this hypothetical C# and the real C# is that your Main method can't look like that, and impure library methods don't return IO values.
The point of the article isn't to recommend this style of programming. You can't, really, since it relies on the counter-factual assumption that all impure library methods return IO. The point of the article is to explain how a language like Haskell uses the type system to distinguish between pure functions and impure actions.
Perhaps the code in that Main method isn't the prettiest code you've ever seen, but we can make it a little nicer. That's the topic of the next article in the series.
Next: Syntactic sugar for IO.
Comments
Why is the input of the IO constructor of type Lazy<T> instead of just type T?
Tyson, thank you for writing. A future article in this article series will answer that question 😀
FWIW, the promised article is now available.
Ah, sure. I was thinking that IO<T> is a monad (in T), so there should be a constructor with argument T. However, the function doens't need to be a constructor. The lambda expression t => new IO<T>(new Lazy<T>(() => t)) satisifies the requirement.
Yes 👍
The IO Container
How a type system can distinguish between pure and impure code.
Referential transparency is the foundation of functional architecture. If you categorise all operations into pure functions and impure actions, then most other traits associated with functional programming follow.
Unfortunately, mainstream programming languages don't distinguish between pure functions and impure actions. Identifying pure functions is tricky, and the knowledge is fleeting. What was a pure function today may become impure next time someone changes the code.
Separating pure and impure code is important. It'd be nice if you could automate the process. Perhaps you could run some tests, or, even better, make the compiler do the work. That's what Haskell and a few other languages do.
In Haskell, the distinction is made with a container called IO. This static type enforces the functional interaction law at compile time: pure functions can't invoke impure actions.
Opaque container #
Regular readers of this blog know that I often use Haskell to demonstrate principles of functional programming. If you don't know Haskell, however, its ability to guarantee the functional interaction law at compile time may seem magical. It's not.
Fortunately, the design is so simple that it's easy to explain the fundamental concept: Results of impure actions are always enclosed in an opaque container called IO. You can think of it as a box with a label.

The label only tells you about the static type of the value inside the box. It could be an int, a DateTime, or your own custom type, say Reservation. While you know what type of value is inside the box, you can't see what's in it, and you can't open it.
Name #
The container itself is called IO, but don't take the word too literally. While all I/O (input/output) is inherently impure, other operations that you don't typically think of as I/O is impure as well. Generation of random numbers (including GUIDs) is the most prominent example. Random number generators rely on the system clock, which you can think of as an input device, although I think many programmers don't.
I could have called the container Impure instead, but I chose to go with IO, since this is the word used in Haskell. It also has the advantage of being short.
What's in the boooox? #
A question frequently comes up: How do I get the value out of my IO? As always, the answer is mu. You don't. You inject the desired behaviour into the container. This goes for all monads, including IO.
But naturally you wonder: If you can't see the value inside the IO box then what's the point?
The point is to enforce the functional interaction law at the type level. A pure function that calls an impure action will receive a sealed, opaque IO box. There's no API that enables a pure function to extract the contents of the container, so this effectively enforces the rule that pure functions can't call impure actions.
The other three types of interactions are still possible.
- Pure functions should be able to call pure functions. Pure functions return 'normal' values (i.e. values not hidden in IO boxes), so they can call each other as usual.
- Impure actions should be able to call pure functions. This becomes possible because you can inject pure behaviour into any monad. You'll see example of that in later articles in this series.
- Impure actions should be able to call other impure actions. Likewise, you can compose many IO actions into one IO action via the IO API.
On the other hand, if you're already inside the box, you can see the contents. And there's one additional rule: If you're already inside an IO box, you can open other IO boxes and see their contents!
In subsequent articles in this article series, you'll see how all of this manifests as C# code. This article gives a high-level view of the concept. I suggest that you go back and re-read it once you've seen the code.
The many-worlds interpretation #
If you're looking for metaphors or other ways to understand what's going on, there's two perspectives I find useful. None of them offer the full picture, but together, I find that they help.
A common interpretation of IO is that it's like the box in which you put Schrödinger's cat. IO<Cat> can be viewed as the superposition of the two states of cat (assuming that Cat is basically a sum type with the cases Alive and Dead). Likewise, IO<int> represents the superposition of all 4,294,967,296 32-bit integers, IO<string> the superposition of infinitely many strings, etcetera.
Only when you observe the contents of the box does the superposition collapse to a single value.
But... you can't observe the contents of an IO box, can you?
The black hole interpretation #
The IO container represents an impenetrable barrier between the outside and the inside. It's like a black hole. Matter can fall into a black hole, but no information can escape its event horizon.
In high school I took cosmology, among many other things. I don't know if the following is still current, but we learned a formula for calculating the density of a black hole, based on its mass. When you input the estimated mass of the universe, the formula suggests a density near vacuum. Wait, what?! Are we actually living inside a black hole? Perhaps. Could there be other universes 'inside' black holes?
The analogy to the IO container seems apt. You can't see into a black hole from the outside, but once beyond the blue event horizon, you can observe everything that goes on in that interior universe. You can't escape to the original universe, though.
As with all metaphors, this one breaks down if you think too much about it. Code running in IO can unpack other IO boxes, even nested boxes. There's no reason to believe that if you're inside a black hole that you can then gaze beyond the event horizon of nested black holes.
Code examples #
In the next articles in this series, you'll see C# code examples that illustrate how this concept might be implemented. The purpose of these code examples is to give you a sense for how IO works in Haskell, but with more familiar syntax.
- IO container in a parallel C# universe
- Syntactic sugar for IO
- Referential transparency of IO
- Implementation of the C# IO container
- Task asynchronous programming as an IO surrogate
Conclusion #
When you saw the title, did you think that this would be an article about IoC Containers? It's not. The title isn't a typo, and I never use the term IoC Container. As Steven and I explain in our book, Inversion of Control (IoC) is a broader concept than Dependency Injection (DI). It's called a DI Container.
IO, on the other hand, is a container of impure values. Its API enables you to 'build' bigger structures (programs) from smaller IO boxes. You can compose IO actions together and inject pure functions into them. The boxes, however, are opaque. Pure functions can't see their contents. This effectively enforces the functional interaction law at the type level.
Comments
Come on, you know there is a perfect metaphor. Monads are like burritos.
Christer, I appreciate that this is all in good fun 🤓
For the benefit of readers who may still be trying to learn these concepts, I'll point out that just as this isn't an article about IoC containers, it's not a monad tutorial. It's an explanation of a particular API called IO, which, among other traits, also forms a monad. I'm trying to downplay that aspect here, because I hope that you can understand most of this and the next articles without knowing what a monad is.
"While you know what type of value is inside the box, you can't see what's in it, and you can't open it."
Well you technically can, with unsafePerformIO ;) although it defeats the whole purpose.
Retiring old service versions
A few ideas on how to retire old versions of a web service.
I was recently listening to a .NET Rocks! episode on web APIs, and one of the topics that came up was how to retire old versions of a web service. It's not easy to do, but not necessarily impossible.
The best approach to API versioning is to never break compatibility. As long as there's no breaking changes, you don't have to version your API. It's rarely possible to completely avoid breaking changes, but the fewer of those that you introduce, the fewer API version you have to maintain. I've previously described how to version REST APIs, but this article doesn't assume any particular versioning strategy.
Sooner or later you'll have an old version that you'd like to retire. How do you do that?
Incentives #
First, take a minute to understand why some clients keep using old versions of your API. It may be obvious, but I meet enough programmers who never give incentives a thought that I find it worthwhile to point out.
When you introduce a breaking change, by definition this is a change that breaks clients. Thus, upgrading from an old version to a newer version of your API is likely to give client developers extra work. If what they have already works to their satisfaction, why should they upgrade their clients?
You might argue that your new version is 'better' because it has more features, or is faster, or whatever it is that makes it better. Still, if the old version is good enough for a particular purpose, some clients are going to stay there. The client maintainers have no incentives to upgrade. There's only cost, and no benefit, to upgrading.
Even if the developers who maintain those clients would like to upgrade, they may be prohibited from doing so by their managers. If there's no business reason to upgrade, efforts are better used somewhere else.
Advance warning #
Web services exist in various contexts. Some are only available on an internal network, while others are publicly available on the internet. Some require an authentication token or API key, while others allow anonymous client access.
With some services, you have a way to contact every single client developer. With other services, you don't know who uses your service.
Regardless of the situation, when you wish to retire a version, you should first try to give clients advance warning. If you have an address list of all client developers, you can simply write them all, but you can't expect that everyone reads their mail. If you don't know the clients, you can publish the warning. If you have a blog or a marketing site, you can publish the warning there. If you run a mailing list, you can write about the upcoming change there. You can tweet it, post it on Facebook, or dance it on TikTok.
Depending on SLAs and contracts, there may even be a legally valid communications channel that you can use.
Give advance warning. That's the decent thing to do.
Slow it down #
Even with advance warning, not everyone gets the message. Or, even if everyone got the message, some people deliberately decide to ignore it. Consider their incentives. They may gamble that as long as your logs show that they use the old version, you'll keep it online. What do you do then?
You can, of course, just take the version off line. That's going to break clients that still depend on that version. That's rarely the best course of action.
Another option is to degrade the performance of that version. Make it slower. You can simply add a constant delay when clients access that service, or you can gradually degrade performance.
Many HTTP client libraries have long timeouts. For example, the default HttpClient timeout is 100 seconds. Imagine that you want to introduce a gradual performance degradation that starts at no delay on June 1, 2020 and reaches 100 seconds after one year. You can use the formula d = 100 s * (t - t0) / 1 year, where d is the delay, t is the current time, and t0 is the start time (e.g. June 1, 2020). This'll cause requests for resources to gradually slow down. After a year, clients still talking to the retiring version will begin to time out.
You can think of this as another way to give advance warning. With the gradual deterioration of performance, users will likely notice the long wait times well before calls actually time out.
When client developers contact you about the bad performance, you can tell them that the issue is fixed in more recent versions. You've just given the client organisation an incentive to upgrade.
Failure injection #
Another option is to deliberately make the service err now and then. Randomly return a 500 Internal Server Error from time to time, even if the service can handle the request.
Like deliberate performance degradation, you can gradually make the deprecated version more and more unreliable. Again, end users are likely to start complaining about the unreliability of the system long before it becomes entirely useless.
Reverse proxy #
One of the many benefits of HTTP-based services is that you can put a reverse proxy in front of your application servers. I've no idea how to configure or operate NGINX or Varnish, but from talking to people who do know, I get the impression that they're quite scriptable.
Since the above ideas are independent of actual service implementation or behaviour, it's a generic problem that you should seek to address with general-purpose software.
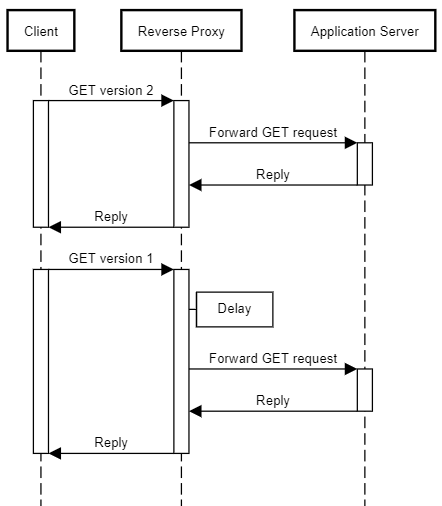
Imagine having a general-purpose reverse proxy that detects whether incoming HTTP requests are for the version you'd like to retire (version 1 in the diagram) or another version. If the proxy detects that the request is for a retiring version, it inserts a delay before it forward the request to the application server. For all requests for current versions, it just forwards the request.
I could imagine doing something similar with failure injections.
Legal ramifications #
All of the above are only ideas. If you can use them, great. Consider the implications, though. You may be legally obliged to keep an SLA. In that case, you can't degrade the performance or reliability below the SLA level.
In any case, I don't think you should do any of these things lightly. Involve relevant stakeholders before you engage in something like the above.
Legal specialists are as careful and conservative as traditional operations teams. Their default reaction to any change proposal is to say no. That's not a judgement on their character or morals, but simply another observation based on incentives. As long as everything works as it's supposed to work, any change represents a risk. Legal specialists, like operations teams, are typically embedded in incentive systems that punish risk-taking.
To counter other stakeholders' reluctance to engage in unorthodox behaviour, you'll have to explain why retiring an old version of the service is important. It works best if you can quantify the reason. If you can, measure how much extra time you waste on maintaining the old version. If the old version runs on separate hardware, or a separate cloud service, quantify the cost overhead.
If you can't produce a compelling argument to retire an old version, then perhaps it isn't that important after all.
Logs #
Server logs can be useful. They can tell you how many requests the old version serves, which IP addresses they come from, at which times or dates you have most traffic, and whether the usage trend is increasing or decreasing.
These measures can be used to support your argument that a particular version should be retired.
Conclusion #
Versioning web services is already a complex subject, but once you've figured it out, you'll sooner or later want to retire an old version of your API. If some clients still make good use of that version, you'll have to give them incentive to upgrade to a newer version.
It's best if you can proactively make clients migrate, so prioritise amiable solutions. Sometimes, however, you have no way to reach all client developers, or no obvious way to motivate them to upgrade. In those cases, gentle and gradual performance or reliability degradation of deprecated versions could be a way.
I present these ideas as nothing more than that: ideas. Use them if they make sense in your context, but think things through. The responsibility is yours.
Comments
Hi Mark. As always an excellent piece. A few comments if I may.
An assumption seems to be, that the client is able to update to a new version of the API, but is not inclined to do so for various reasons. I work with organisations where updating a client if nearly impossible. Not because of lack of will, but due to other factors such as government regulations, physical location of client, hardware version or capabilities of said client to name just a few.
We have a tendency in the software industry to see updates as a question of 'running Windows update' and then all is good. Most likely because that is the world we live in. If we wish to update a program or even an OS, it is fairly easy even your above considerations taken into account.
In the 'physical' world of manufacturing (or pharmacy or mining or ...) the situation is different. The lifetime of the 'thing' running the client is regularly measured in years or even decades and not weeks or months as it is for a piece of software.
Updates are often equal to bloating of resource requirements meaning you have to replace the hardware. This might not always be possible again for various reasons. Cost (company is pressed on margin or client is located in Outer Mongolia) or risk (client is located in Syria or some other hotspot) are some I've personally come across.
REST/HTTP is not used. I acknowledge that the original podcast from .NET Rocks! was about updating a web service. This does not change the premises of your arguments, but it potentially adds a layer of complication.
Karsten, thank you for writing. You are correct that the underlying assumption is that you can retire old versions.
I, too, have written REST APIs where retiring service versions weren't an option. These were APIs that consumer-grade hardware would communicate with. We had no way to assure that consumers would upgrade their hardware. Those boxes wouldn't have much of a user-interface. Owners might not realise that firmware updates were available, even if they were.
This article does, indeed, assume that the reader has made an informed decision that it's fundamentally acceptable to retire a service version. I should have made that more explicit.
Where's the science?
Is a scientific discussion about software development possible?
Have you ever found yourself in a heated discussion about a software development topic? Which is best? Tabs or spaces? Where do you put the curly brackets? Is significant whitespace a good idea? Is Python better than Go? Does test-driven development yield an advantage? Is there a silver bullet? Can you measure software development productivity?
I've had plenty of such discussions, and I'll have them again in the future.
While some of these discussions may resemble debates on how many angels can dance on the head of a pin, other discussions might be important. Ex ante, it's hard to tell which is which.
Why don't we settle these discussions with science?
A notion of science #
I love science. Why don't I apply scientific knowledge instead of arguments based on anecdotal evidence?
To answer such questions, we must first agree on a definition of science. I favour Karl Popper's description of empirical falsifiability. A hypothesis that makes successful falsifiable predictions of the future is a good scientific theory. Such a a theory has predictive power.
Newton's theory of gravity had ample predictive power, but Einstein's theory of general relativity supplanted it because its predictive power was even better.
Mendel's theory of inheritance had predictive power, but was refined into what is modern-day genetics which yields much greater predictive power.
Is predictive power the only distinguishing trait of good science? I'm already venturing into controversial territory by taking this position. I've met people in the programming community who consider my position naive or reductionist.
What about explanatory power? If a theory satisfactorily explains observed phenomena, doesn't that count as a proper scientific theory?
Controversy #
I don't believe in explanatory power as a sufficient criterion for science. Without predictive power, we have little evidence that an explanation is correct. An explanatory theory can even be internally consistent, and yet we may not know if it describes reality.
Theories with explanatory power are the realm of politics or religion. Consider the observation that some people are rich and some are poor. You can believe in a theory that explains this by claiming structural societal oppression. You can believe in another theory that views poor people as fundamentally lazy. Both are (somewhat internally consistent) political theories, but they have yet to demonstrate much predictive power.
Likewise, you may believe that some deity created the universe, but that belief produces no predictions. You can apply Occam's razor and explain the same phenomena without a god. A belief in one or more gods is a religious theory, not a scientific theory.
It seems to me that there's a correlation between explanatory power and controversy. Over time, theories with predictive power become uncontroversial. Even if they start out controversial (such as Einstein's theory of general relativity), the dust soon settles because it's hard to argue with results.
Theories with mere explanatory power, on the other hand, can fuel controversy forever. Explanations can be compelling, and without evidence to refute them, the theories linger.
Ironically, you might argue that Popper's theory of scientific discovery itself is controversial. It's a great explanation, but does it have predictive power? Not much, I admit, but I'm also not aware of competing views on science with better predictive power. Thus, you're free to disagree with everything in this article. I admit that it's a piece of philosophy, not of science.
The practicality of experimental verification #
We typically see our field of software development as one of the pillars of STEM. Many of us have STEM educations (I don't; I'm an economist). Yet, we're struggling to come to grips with the lack of scientific methodology in our field. It seems to me that we suffer from physics envy.
It's really hard to compete with physics when it comes to predictive power, but even modern physics struggle with experimental verification. Consider an establishment like CERN. It takes billions of euros of investment to make today's physics experiments possible. The only reason we make such investments, I think, is that physics so far has had a good track record.
What about another fairly 'hard' science like medicine? In order to produce proper falsifiable predictions, medical science have evolved the process of the randomised controlled trial. It works well when you're studying short-term effects. Does this medicine cure this disease? Does this surgical procedure improve a patient's condition? How does lack of REM sleep for three days affect your ability to remember strings of numbers?
When a doctor tells you that a particular medicine helps, or that surgery might be warranted, he or she is typically on solid scientific grounds.
Here's where things start to become less clear, though, What if a doctor tells you that a particular diet will improve your expected life span? Is he or she on scientific solid ground?
That's rarely the case, because you can't make randomised controlled trials about life styles. Or, rather, a totalitarian society might be able to do that, but we'd consider it unethical. Consider what it would involve: You'd have to randomly select a significant number of babies and group them into those who must follow a particular life style, and those who must not. Then you'll somehow have to force those people to stick to their randomly assigned life style for the entirety of their lives. This is not only unethical, but the experiment also takes the most of a century to perform.
What life-style scientists instead do is resort to demographic studies, with all the problems of statistics they involve. Again, the question is whether scientific theories in this field offer predictive power. Perhaps they do, but it takes decades to evaluate the results.
My point is that medicine isn't exclusively a hard science. Some medicine is, and some is closer to social sciences.
I'm an economist by education. Economics is generally not considered a hard science, although it's a field where it's trivial to make falsifiable predictions. Almost all of economics is about numbers, so making a falsifiable prediction is trivial: The MSFT stock will be at 200 by January 1 2021. The unemployment rate in Denmark will be below 5% in third quarter of 2020. The problem with economics is that most of such predictions turn out to be no better than the toss of a coin - even when made by economists. You can make falsifiable predictions in economics, but most of them do, in fact, get falsified.
On the other hand, with the advances in such disparate fields as DNA forensics, satellite surveys, and computer-aided image processing, a venerable 'art' like archaeology is gaining predictive power. We predict that if we dig here, we'll find artefacts from the iron age. We predict that if we make a DNA test of these skeletal remains, they'll show that the person buried was a middle-aged women. And so on.
One thing is the ability to produce falsifiable predictions. Another things is whether or not the associated experiment is practically possible.
The science of software development #
Do we have a science of software development? I don't think that we have.
There's computer science, but that's not quite the same. That field of study has produced many predictions that hold. In general, quicksort will be faster than bubble sort. There's an algorithm for finding the shortest way through a network. That sort of thing.
You will notice that these result are hardly controversial. It's not those topics that we endlessly debate.
We debate whether certain ways to organise work is more 'productive'. The entire productivity debate revolves around an often implicit context: that what we discuss is long-term productivity. We don't much argue how to throw together something during a weekend hackaton. We argue whether we can complete a nine-month software project safer with test-driven development. We argue whether a code base can better sustain its organisation year after year if it's written in F# or JavaScript.
There's little scientific evidence on those questions.
The main problem, as I see it, is that it's impractical to perform experiments. Coming up with falsifiable predictions is easy.
Let's consider an example. Imagine that your hypothesis is that test-driven development makes you more productive in the middle and long run. You'll have to turn that into a falsifiable claim, so first, pick a software development project of sufficient complexity. Imagine that you can find a project that someone estimates will take around ten months to complete for a team of five people. This has to be a real project that someone needs done, complete with vague, contradictory, and changing requirements. Now you formulate your falsifiable prediction, for example: "This project will be delivered one month earlier with test-driven development."
Next, you form teams to undertake the work. One team to perform the work with test-driven development, and one team to do the work without it. Then you measure when they're done.
This is already impractical, because who's going to pay for two teams when one would suffice?
Perhaps, if you're an exceptional proposal writer, you could get a research grant for that, but alas, that wouldn't be good enough.
With two competing teams of five people each, it might happen that one team member exhibits productivity orders of magnitudes different from the others. That could skew the experimental outcome, so you'd have to go for a proper randomised controlled trial. This would involve picking numerous teams and assigning a methodology at random: either they do test-driven development, or they don't. Nothing else should vary. They should all use the same programming language, the same libraries, the same development tools, and work the same hours. Furthermore, no-one outside the team should know which teams follow which method.
Theoretically possible, but impractical. It would require finding and paying many software teams for most of a year. One such experiment would cost millions of euros.
If you did such an experiment, it would tell you something, but it'd still be open to interpretation. You might argue that the programming language used caused the outcome, but that one can't extrapolate from that result to other languages. Or perhaps there was something special about the project that you think doesn't generalise. Or perhaps you take issue with the pool from which the team members were drawn. You'd have to repeat the experiment while varying one of the other dimensions. That'll cost millions more, and take another year.
Considering the billions of euros/dollars/pounds the world's governments pour into research, you'd think that we could divert a few hundred millions to do proper research in software development, but it's unlikely to happen. That's the reason we have to contend ourselves with arguing from anecdotal evidence.
Conclusion #
I can imagine how scientific inquiry into software engineering could work. It'd involve making a falsifiable prediction, and then set up an experiment to prove it wrong. Unfortunately, to be on a scientifically sound footing, experiments should be performed with randomised controlled trials, with a statistically significant number of participants. It's not too hard to conceive of such experiments, but they'd be prohibitively expensive.
In the meantime, the software development industry moves forward. We share ideas and copy each other. Some of us are successful, and some of us fail. Slowly, this might lead to improvements.
That process, however, looks more like evolution than scientific progress. The fittest software development organisations survive. They need not be the best, as they could be stuck in local maxima.
When we argue, when we write blog posts, when we speak at conferences, when we appear on podcasts, we exchange ideas and experiences. Not genes, but memes.
Comments
That topic is something many software developers think about, at least I do from time to time.
Your post reminded me of that conference talk Intro to Empirical Software Engineering: What We Know We Don't Know by Hillel Wayne. Just curious - have you seen the talk and if so - what do you think? Researches mentioned in the talk are not proper scientific expreiments as you describe, but anyway looked really interesting to me.
Sergey, thank you for writing. I didn't know about that talk, but Hillel Wayne regularly makes an appearance in my Twitter feed. I've now seen the talk, and I think it offers a perspective close to mine.
I've already read The Leprechauns of Software Engineering (above, I linked to my review), but while I was aware of Making Software, I've yet to read it. Several people have reacted to my article by recommending that book, so it's now on it's way to me in the mail.
Modelling versus shaping reality
How does software development relate to reality?
I recently appeared as a guest on the .NET Rocks! podcast where we discussed Fred Brooks' 1986 essay No Silver Bullet. As a reaction, Jon Suda wrote a thoughtful piece of his own. That made me think some more.
Beware of Greeks... #
Brooks' central premise is Aristotle's distinction between essential and accidental complexity. I've already examined the argument in my previous article on the topic, but in summary, Brooks posits that complexity in software development can be separated into those two categories:
c = E + a
Here, c is the total complexity, E is the essential complexity, and a the accidental complexity. I've deliberately represented c and a with lower-case letters to suggest that they represent variables, whereas I mean to suggest with the upper-case E that the essential complexity is constant. That's Brooks' argument: Every problem has an essential complexity that can't be changed. Thus, your only chance to reduce total complexity c is to reduce the accidental complexity a.
Jon Suda writes that
That got me thinking, because actually I do. When I wrote Yes silver bullet I wanted to engage with Brooks' essay on its own terms."Mark doesn’t disagree with the classification of problems"
I do think, however, that one should be sceptical of any argument originating from the ancient Greeks. These people believed that all matter was composed of earth, water, air, and fire. They believed in the extramission theory of vision. They practised medicine by trying to balance blood, phlegm, yellow, and black bile. Aristotle believed in spontaneous generation. He also believed that the brain was a radiator while the heart was the seat of intelligence.
I think that Aristotle's distinction between essential and accidental complexity is a false dichotomy, at least in the realm of software development.
The problem is the assumption that there's a single, immutable underlying reality to be modelled.
Modelling reality #
Jon Suda touches on this as well:
I agree that the 'real world' (whatever it is) is often messy, and our ability to deal with the mess is how we earn our keep. It seems to me, though, that there's an underlying assumption that there's a single real world to be modelled."Conceptual (or business) problems are rooted in the problem domain (i.e., the real world)[...]"
"Dealing with the "messy real world" is what makes software development hard these days"
I think that a more fruitful perspective is to question that assumption. Don’t try to model the real world, it doesn’t exist.
I've mostly worked with business software. Web shops, BLOBAs, and other software to support business endeavours. This is the realm implicitly addressed by Domain-Driven Design and a technique like behaviour-driven development. The assumption is that there's one or more domain experts who know how the business operates, and the job of the software development team is to translate that understanding into working software.
This is often the way it happens. Lord knows that I've been involved in enough fixed-requirements contracts to know that sometimes, all you can do is try to implement the requirements as best you can, regardless of how messy they are. In other words, I agree with Jon Suda that messy problems are a reality.
Where I disagree with Brooks and Aristotle is that business processes contain essential complexity. In the old days, before computers, businesses ran according to a set of written and unwritten rules. Routine operations might be fairly consistent, but occasionally, something out of the ordinary would happen. Organisations don't have a script for every eventuality. When the unexpected happens, people wing it.
A business may have a way it sells its goods. It may have a standard price list, and a set of discounts that salespeople are authorised to offer. It may have standard payment terms that customers are expected to comply with. It may even have standard operating procedures for dealing with missing payments.
Then one day, say, the German government expresses interest in placing an order greater than the business has ever handled before. The Germans, however, want a special discount, and special terms of payment. What happens? Do the salespeople refuse because those requests don't comply with the way the organisation does business? Of course not. The case is escalated to people with the authority to change the rules, and a deal is made.
Later, the French government comes by, and a similar situation unfolds, but with the difference that someone else handles the French, and the deal struck is different.
The way these two cases are handled could be internally inconsistent. Decisions are made based on concrete contexts, but with incomplete information and based on gut feelings.
While there may be a system to how an organisation does routine business, there's no uniform reality to be modelled.
You can model standard operating procedures in software, but I think it's a mistake to think that it's a model of reality. It's just an interpretation on how routine business is conducted.
There's no single, unyielding essential complexity, because the essence isn't there.
Shaping reality #
Dan North tells a story of a project where a core business requirement was the ability to print out data. When investigating the issue, it turned out that users needed to have the printout next to their computers so that they could type the data into another system. When asked whether they wouldn't rather prefer to have the data just appear in the other system, they incredulously replied, "You can do that?!
This turns out to be a common experience. Someone may tell you about an essential requirement, but when you investigate, it turns out to be not at all essential. There may not be any essential complexity.
There's likely to be complexity, but the distinction between essential and accidental complexity seems artificial. While software can model business processes, it can also shape reality. Consider a company like Amazon. The software that supports Amazon wasn't developed after the company was already established. Amazon developed it concurrently with setting up business.
Consider companies like Google, Facebook, Uber, or Airbnb. Such software doesn't model reality; it shapes reality.
In the beginning of the IT revolution, the driving force behind business software development was to automate existing real-world processes, but this is becoming increasingly rare. New companies enter the markets digitally born. Older organisations may be on their second or third system since they went digital. Software not only models 'messy' reality - it shapes 'messy' reality.
Conclusion #
It may look as though I fundamentally disagree with Jon Suda's blog post. I don't. I agree with almost all of it. It did, however, inspire me to put my thoughts into writing.
My position is that I find the situation more nuanced than Fred Brooks suggests by setting off from Aristotle. I don't think that the distinction between essential and accidental complexity is the whole story. Granted, it provides a fruitful and inspiring perspective, but while we find it insightful, we shouldn't accept it as gospel.
Comments
I think I agree with virtually everything said here – if not actually everything 😊
As (virtually, if not actually) always, though, there are a few things I’d like to add, clarify, and elaborate on 😊
I fully share your reluctance to accept ancient Greek philosophy. I once discussed No Silver Bullet (and drank Scotch) with a (non-developer) “philosopher” friend of mine. (Understand: He has a BA in philosophy 😊) He said something to the effect of do you understand this essence/accident theory is considered obsolete? I answered that it was beside the point here – at least as far as I was concerned. For me, the dichotomy serves as an inspiration, a metaphor perhaps, not a rigorous theoretical framework – that’s one of the reasons why I adapted it into the (informal) conceptual/technical distinction.
I also 100% agree with the notion that software shouldn’t merely “model” or “automate” reality. In fact, I now remember that back in university, this was one of the central themes of my “thesis” (or whatever it was). I pondered the difference/boundary between analysis and design activities and concluded that the idea of creating a model of the “real world” during analysis and then building a technical representation of this model as part of design/implementation couldn’t adequately describe many of the more “inventive” software projects and products.
I don’t, however, believe this makes the conceptual/technical (essential/accidental) distinction go away. Even though the point of a project may not (and should not) be a mere automation of a preexisting reality, you still need to know what you want to achieve (i.e., “invent”), conceptually, to be able to fashion a technical implementation of it. And yes, your conceptual model should be based on what’s possible with all available technology – which is why you’ll hopefully end up with something way better than the old solution. (Note that in my post, I never talk about “modeling” the “messy real world” but rather “dealing with it”; even your revolutionary new solution will have to coexist with the messy outside world.)
For me, one of the main lessons of No Silver Bullet, the moral of the story, is this: Developers tend to spend inordinate amounts of time discussing and brooding over geeky technical stuff; perhaps they should, instead, talk to their users a bit more and learn something about the problem domain; that’s where the biggest room for improvement is, in my opinion.
FWIW
https://jonsmusings.com/Transmutation-of-Reality
Let the inspiration feedback loop continue 😊 I agree with more-or-less everything you say; I just don’t necessarily think that your ideas are incompatible with those expressed in No Silver Bullet. That, to a significant extent (but not exclusively), is what my new post is about. As I said in my previous comment, your article reminded me of my university “thesis,” and I felt that the paper I used as its “conceptual framework” was worth presenting in a “non-academic” form. It can mostly be used to support your arguments – I certainly use it that way.

Comments
This sounds like a great approach. I have been on projects with tests that involved the database, but none of them were designed as well as this. I will be sure to come back to this post when we add a database to my current project.
My understanding is that SQL Server Express and LocalDB are not the same thing. Are you using SQL Server Express or LocalDB? Do you prefer one over the other for this database testing approach of yours?
Tyson, thank you for writing. It's not really my area of expertise. I use the one bundled with Visual Studio, so I suppose that's actually LocalDB, and not SQL Server Express.