ploeh blog danish software design
Serializing restaurant tables in F#
Using System.Text.Json, with and without Reflection.
This article is part of a short series of articles about serialization with and without Reflection. In this instalment I'll explore some options for serializing JSON with F# using the API built into .NET: System.Text.Json. I'm not going use Json.NET in this article, but I've done similar things with that library in the past, so what's here is, at least, somewhat generalizable.
Natural numbers #
Before we start investigating how to serialize to and from JSON, we must have something to serialize. As described in the introductory article we'd like to parse and write restaurant table configurations like this:
{
"singleTable": {
"capacity": 16,
"minimalReservation": 10
}
}
On the other hand, I'd like to represent the Domain Model in a way that encapsulates the rules governing the model, making illegal states unrepresentable.
As the first step, we observe that the numbers involved are all natural numbers. In F# it's both idiomatic and easy to define a predicative data type:
type NaturalNumber = private NaturalNumber of int
Since it's defined with a private constructor we need to also supply a way to create valid values of the type:
module NaturalNumber = let tryCreate n = if n < 1 then None else Some (NaturalNumber n)
In this, as well as the other articles in this series, I've chosen to model the potential for errors with Option values. I could also have chosen to use Result if I wanted to communicate information along the 'error channel', but sticking with Option makes the code a bit simpler. Not so much in F# or Haskell, but once we reach C#, applicative validation becomes complicated.
There's no loss of generality in this decision, since both Option and Result are applicative functors.
> NaturalNumber.tryCreate -1;;
val it: NaturalNumber option = None
> let x = NaturalNumber.tryCreate 42;;
val x: NaturalNumber option = Some NaturalNumber 42
The tryCreate function enables client developers to create NaturalNumber values, and due to the F#'s default equality and comparison implementation, you can even compare them:
> let y = NaturalNumber.tryCreate 2112;;
val y: NaturalNumber option = Some NaturalNumber 2112
> x < y;;
val it: bool = true
That's it for natural numbers. Three lines of code. Compare that to the Haskell implementation, which required eight lines of code. This is mostly due to F#'s private keyword, which Haskell doesn't have.
Domain Model #
Modelling a restaurant table follows in the same vein. One invariant I would like to enforce is that for a 'single' table, the minimal reservation should be a NaturalNumber less than or equal to the table's capacity. It doesn't make sense to configure a table for four with a minimum reservation of six.
In the same spirit as above, then, define this type:
type Table = private | SingleTable of NaturalNumber * NaturalNumber | CommunalTable of NaturalNumber
Once more the private keyword makes it impossible for client code to create instances directly, so we need a pair of functions to create values:
module Table = let trySingle capacity minimalReservation = option { let! cap = NaturalNumber.tryCreate capacity let! min = NaturalNumber.tryCreate minimalReservation if cap < min then return! None else return SingleTable (cap, min) } let tryCommunal = NaturalNumber.tryCreate >> Option.map CommunalTable
Notice that trySingle checks the invariant that the capacity must be greater than or equal to the minimalReservation.
Again, notice how much easier it is to define a predicative type in F#, compared to Haskell.
This isn't a competition between languages, and while F# certainly scores a couple of points here, Haskell has other advantages.
The point of this little exercise, so far, is that it encapsulates the contract implied by the Domain Model. It does this by using the static type system to its advantage.
JSON serialization by hand #
At the boundaries of applications, however, there are no static types. Is the static type system still useful in that situation?
For a long time, the most popular .NET library for JSON serialization was Json.NET, but these days I find the built-in API offered in the System.Text.Json namespace adequate. This is also the case here.
The original rationale for this article series was to demonstrate how serialization can be done without Reflection, so I'll start there and return to Reflection later.
In this article series, I consider the JSON format fixed. A single table should be rendered as shown above, and a communal table should be rendered like this:
{ "communalTable": { "capacity": 42 } }
Often in the real world you'll have to conform to a particular protocol format, or, even if that's not the case, being able to control the shape of the wire format is important to deal with backwards compatibility.
As I outlined in the introduction article you can usually find a more weakly typed API to get the job done. For serializing Table to JSON it looks like this:
let serializeTable = function | SingleTable (NaturalNumber capacity, NaturalNumber minimalReservation) -> let j = JsonObject () j["singleTable"] <- JsonObject () j["singleTable"]["capacity"] <- capacity j["singleTable"]["minimalReservation"] <- minimalReservation j.ToJsonString () | CommunalTable (NaturalNumber capacity) -> let j = JsonObject () j["communalTable"] <- JsonObject () j["communalTable"]["capacity"] <- capacity j.ToJsonString ()
In order to separate concerns, I've defined this functionality in a new module that references the module that defines the Domain Model. The serializeTable function pattern-matches on SingleTable and CommunalTable to write two different JsonObject objects, using the JSON API's underlying Document Object Model (DOM).
JSON deserialization by hand #
You can also go the other way, and when it looks more complicated, it's because it is. When serializing an encapsulated value, not a lot can go wrong because the value is already valid. When deserializing a JSON string, on the other hand, all sorts of things can go wrong: It might not even be a valid string, or the string may not be valid JSON, or the JSON may not be a valid Table representation, or the values may be illegal, etc.
Here I found it appropriate to first define a small API of parsing functions, mostly in order to make the object-oriented API more composable. First, I need some code that looks at the root JSON object to determine which kind of table it is (if it's a table at all). I found it appropriate to do that as a pair of active patterns:
let private (|Single|_|) (node : JsonNode) = match node["singleTable"] with | null -> None | tn -> Some tn let private (|Communal|_|) (node : JsonNode) = match node["communalTable"] with | null -> None | tn -> Some tn
It turned out that I also needed a function to even check if a string is a valid JSON document:
let private tryParseJson (candidate : string) = try JsonNode.Parse candidate |> Some with | :? System.Text.Json.JsonException -> None
If there's a way to do that without a try/with expression, I couldn't find it. Likewise, trying to parse an integer turns out to be surprisingly complicated:
let private tryParseInt (node : JsonNode) = match node with | null -> None | _ -> if node.GetValueKind () = JsonValueKind.Number then try node |> int |> Some with | :? FormatException -> None // Thrown on decimal numbers else None
Both tryParseJson and tryParseInt are, however, general-purpose functions, so if you have a lot of JSON you need to parse, you can put them in a reusable library.
With those building blocks you can now define a function to parse a Table:
let tryDeserializeTable (candidate : string) = match tryParseJson candidate with | Some (Single node) -> option { let! capacity = node["capacity"] |> tryParseInt let! minimalReservation = node["minimalReservation"] |> tryParseInt return! Table.trySingle capacity minimalReservation } | Some (Communal node) -> option { let! capacity = node["capacity"] |> tryParseInt return! Table.tryCommunal capacity } | _ -> None
Since both serialisation and deserialization is based on string values, you should write automated tests that verify that the code works, and in fact, I did. Here are a few examples:
[<Fact>] let ``Deserialize single table for 4`` () = let json = """{"singleTable":{"capacity":4,"minimalReservation":3}}""" let actual = tryDeserializeTable json Table.trySingle 4 3 =! actual [<Fact>] let ``Deserialize non-table`` () = let json = """{"foo":42}""" let actual = tryDeserializeTable json None =! actual
Apart from module declaration and imports etc. this hand-written JSON capability requires 46 lines of code, although, to be fair, some of that code (tryParseJson and tryParseInt) are general-purpose functions that belong in a reusable library. Can we do better with static types and Reflection?
JSON serialisation based on types #
The static JsonSerializer class comes with Serialize<T> and Deserialize<T> methods that use Reflection to convert a statically typed object to and from JSON. You can define a type (a Data Transfer Object (DTO) if you will) and let Reflection do the hard work.
In Code That Fits in Your Head I explain how you're usually better off separating the role of serialization from the role of Domain Model. One way to do that is exactly by defining a DTO for serialisation, and let the Domain Model remain exclusively to model the rules of the application. The above Table type plays the latter role, so we need new DTO types:
type CommunalTableDto = { Capacity : int } type SingleTableDto = { Capacity : int; MinimalReservation : int } type TableDto = { CommunalTable : CommunalTableDto option SingleTable : SingleTableDto option }
One way to model a sum type with a DTO is to declare both cases as option fields. While it does allow illegal states to be representable (i.e. both kinds of tables defined at the same time, or none of them present) this is only par for the course at the application boundary.
While you can serialize values of that type, by default the generated JSON doesn't have the right format:
> val dto: TableDto = { CommunalTable = Some { Capacity = 42 }
SingleTable = None }
> JsonSerializer.Serialize dto;;
val it: string = "{"CommunalTable":{"Capacity":42},"SingleTable":null}"
There are two problems with the generated JSON document:
- The casing is wrong
- The null value shouldn't be there
None of those are too hard to address, but it does make the API a bit more awkward to use, as this test demonstrates:
[<Fact>] let ``Serialize communal table via reflection`` () = let dto = { CommunalTable = Some { Capacity = 42 }; SingleTable = None } let actual = JsonSerializer.Serialize ( dto, JsonSerializerOptions ( PropertyNamingPolicy = JsonNamingPolicy.CamelCase, IgnoreNullValues = true )) """{"communalTable":{"capacity":42}}""" =! actual
You can, of course, define this particular serialization behaviour as a reusable function, so it's not a problem that you can't address. I just wanted to include this, since it's part of the overall work that you have to do in order to make this work.
JSON deserialisation based on types #
To allow parsing of JSON into the above DTO the Reflection-based Deserialize method pretty much works out of the box, although again, it needs to be configured. Here's a passing test that demonstrates how that works:
[<Fact>] let ``Deserialize single table via reflection`` () = let json = """{"singleTable":{"capacity":4,"minimalReservation":2}}""" let actual = JsonSerializer.Deserialize<TableDto> ( json, JsonSerializerOptions ( PropertyNamingPolicy = JsonNamingPolicy.CamelCase )) { CommunalTable = None SingleTable = Some { Capacity = 4; MinimalReservation = 2 } } =! actual
There's only difference in casing, so you'd expect the Deserialize method to be a Tolerant Reader, but no. It's very particular about that, so the JsonNamingPolicy.CamelCase configuration is necessary. Perhaps the API designers found that explicit is better than implicit.
In any case, you could package that in a reusable Deserialize function that has all the options that are appropriate in a particular code context, so not a big deal. That takes care of actually writing and parsing JSON, but that's only half the battle. This only gives you a way to parse and serialize the DTO. What you ultimately want is to persist or dehydrate Table data.
Converting DTO to Domain Model, and vice versa #
As usual, converting a nice, encapsulated value to a more relaxed format is safe and trivial:
let toTableDto = function | SingleTable (NaturalNumber capacity, NaturalNumber minimalReservation) -> { CommunalTable = None SingleTable = Some { Capacity = capacity MinimalReservation = minimalReservation } } | CommunalTable (NaturalNumber capacity) -> { CommunalTable = Some { Capacity = capacity }; SingleTable = None }
Going the other way is fundamentally a parsing exercise:
let tryParseTableDto candidate = match candidate.CommunalTable, candidate.SingleTable with | Some { Capacity = capacity }, None -> Table.tryCommunal capacity | None, Some { Capacity = capacity; MinimalReservation = minimalReservation } -> Table.trySingle capacity minimalReservation | _ -> None
Such an operation may fail, so the result is a Table option. It could also have been a Result<Table, 'something>, if you wanted to return information about errors when things go wrong. It makes the code marginally more complex, but doesn't change the overall thrust of this exploration.
Ironically, while tryParseTableDto is actually more complex than toTableDto it looks smaller, or at least denser.
Let's take stock of the type-based alternative. It requires 26 lines of code, distributed over three DTO types and the two conversions tryParseTableDto and toTableDto, but here I haven't counted configuration of Serialize and Deserialize, since I left that to each test case that I wrote. Since all of this code generally stays within 80 characters in line width, that would realistically add another 10 lines of code, for a total around 36 lines.
This is smaller than the DOM-based code, although at the same magnitude.
Conclusion #
In this article I've explored two alternatives for converting a well-encapsulated Domain Model to and from JSON. One option is to directly manipulate the DOM. Another option is take a more declarative approach and define types that model the shape of the JSON data, and then leverage type-based automation (here, Reflection) to automatically parse and write the JSON.
I've deliberately chosen a Domain Model with some constraints, in order to demonstrate how persisting a non-trivial data model might work. With that setup, writing 'loosely coupled' code directly against the DOM requires 46 lines of code, while taking advantage of type-based automation requires 36 lines of code. Contrary to the Haskell example, Reflection does seem to edge out a win this round.
Serializing restaurant tables in Haskell
Using Aeson, with and without generics.
This article is part of a short series of articles about serialization with and without Reflection. In this instalment I'll explore some options for serializing JSON using Aeson.
The source code is available on GitHub.
Natural numbers #
Before we start investigating how to serialize to and from JSON, we must have something to serialize. As described in the introductory article we'd like to parse and write restaurant table configurations like this:
{
"singleTable": {
"capacity": 16,
"minimalReservation": 10
}
}
On the other hand, I'd like to represent the Domain Model in a way that encapsulates the rules governing the model, making illegal states unrepresentable.
As the first step, we observe that the numbers involved are all natural numbers. While I'm aware that Haskell has built-in Nat type, I choose not to use it here, for a couple of reasons. One is that Nat is intended for type-level programming, and while this might be useful here, I don't want to pull in more exotic language features than are required. Another reason is that, in this domain, I want to model natural numbers as excluding zero (and I honestly don't remember if Nat allows zero, but I think that it does..?).
Another option is to use Peano numbers, but again, for didactic reasons, I'll stick with something a bit more idiomatic.
You can easily introduce a wrapper over, say, Integer, to model natural numbers:
newtype Natural = Natural Integer deriving (Eq, Ord, Show)
This, however, doesn't prevent you from writing Natural (-1), so we need to make this a predicative data type. The first step is to only export the type, but not its data constructor:
module Restaurants ( Natural, -- More exports here... ) where
But this makes it impossible for client code to create values of the type, so we need to supply a smart constructor:
tryNatural :: Integer -> Maybe Natural tryNatural n | n < 1 = Nothing | otherwise = Just (Natural n)
In this, as well as the other articles in this series, I've chosen to model the potential for errors with Maybe values. I could also have chosen to use Either if I wanted to communicate information along the 'error channel', but sticking with Maybe makes the code a bit simpler. Not so much in Haskell or F#, but once we reach C#, applicative validation becomes complicated.
There's no loss of generality in this decision, since both Maybe and Either are Applicative instances.
With the tryNatural function you can now (attempt to) create Natural values:
ghci> tryNatural (-1) Nothing ghci> x = tryNatural 42 ghci> x Just (Natural 42)
This enables client developers to create Natural values, and due to the type's Ord instance, you can even compare them:
ghci> y = tryNatural 2112 ghci> x < y True
Even so, there will be cases when you need to extract the underlying Integer from a Natural value. You could supply a normal function for that purpose, but in order to make some of the following code a little more elegant, I chose to do it with pattern synonyms:
{-# COMPLETE N #-}
pattern N :: Integer -> Natural
pattern N i <- Natural i
That needs to be exported as well.
So, eight lines of code to declare a predicative type that models a natural number. Incidentally, this'll be 2-3 lines of code in F#.
Domain Model #
Modelling a restaurant table follows in the same vein. One invariant I would like to enforce is that for a 'single' table, the minimal reservation should be a Natural number less than or equal to the table's capacity. It doesn't make sense to configure a table for four with a minimum reservation of six.
In the same spirit as above, then, define this type:
data SingleTable = SingleTable { singleCapacity :: Natural , minimalReservation :: Natural } deriving (Eq, Ord, Show)
Again, only export the type, but not its data constructor. In order to extract values, then, supply another pattern synonym:
{-# COMPLETE SingleT #-}
pattern SingleT :: Natural -> Natural -> SingleTable
pattern SingleT c m <- SingleTable c m
Finally, define a Table type and two smart constructors:
data Table = Single SingleTable | Communal Natural deriving (Eq, Show) trySingleTable :: Integer -> Integer -> Maybe Table trySingleTable capacity minimal = do c <- tryNatural capacity m <- tryNatural minimal if c < m then Nothing else Just (Single (SingleTable c m)) tryCommunalTable :: Integer -> Maybe Table tryCommunalTable = fmap Communal . tryNatural
Notice that trySingleTable checks the invariant that the capacity must be greater than or equal to the minimal reservation.
The point of this little exercise, so far, is that it encapsulates the contract implied by the Domain Model. It does this by using the static type system to its advantage.
JSON serialization by hand #
At the boundaries of applications, however, there are no static types. Is the static type system still useful in that situation?
For Haskell, the most common JSON library is Aeson, and I admit that I'm no expert. Thus, it's possible that there's an easier way to serialize to and deserialize from JSON. If so, please leave a comment explaining the alternative.
The original rationale for this article series was to demonstrate how serialization can be done without Reflection, or, in the case of Haskell, Generics (not to be confused with .NET generics, which in Haskell usually is called parametric polymorphism). We'll return to Generics later in this article.
In this article series, I consider the JSON format fixed. A single table should be rendered as shown above, and a communal table should be rendered like this:
{ "communalTable": { "capacity": 42 } }
Often in the real world you'll have to conform to a particular protocol format, or, even if that's not the case, being able to control the shape of the wire format is important to deal with backwards compatibility.
As I outlined in the introduction article you can usually find a more weakly typed API to get the job done. For serializing Table to JSON it looks like this:
newtype JSONTable = JSONTable Table deriving (Eq, Show) instance ToJSON JSONTable where toJSON (JSONTable (Single (SingleT (N c) (N m)))) = object ["singleTable" .= object [ "capacity" .= c, "minimalReservation" .= m]] toJSON (JSONTable (Communal (N c))) = object ["communalTable" .= object ["capacity" .= c]]
In order to separate concerns, I've defined this functionality in a new module that references the module that defines the Domain Model. Thus, to avoid orphan instances, I've defined a JSONTable newtype wrapper that I then make a ToJSON instance.
The toJSON function pattern-matches on Single and Communal to write two different Values, using Aeson's underlying Document Object Model (DOM).
JSON deserialization by hand #
You can also go the other way, and when it looks more complicated, it's because it is. When serializing an encapsulated value, not a lot can go wrong because the value is already valid. When deserializing a JSON string, on the other hand, all sorts of things can go wrong: It might not even be a valid string, or the string may not be valid JSON, or the JSON may not be a valid Table representation, or the values may be illegal, etc.
It's no surprise, then, that the FromJSON instance is bigger:
instance FromJSON JSONTable where parseJSON (Object v) = do single <- v .:? "singleTable" communal <- v .:? "communalTable" case (single, communal) of (Just s, Nothing) -> do capacity <- s .: "capacity" minimal <- s .: "minimalReservation" case trySingleTable capacity minimal of Nothing -> fail "Expected natural numbers." Just t -> return $ JSONTable t (Nothing, Just c) -> do capacity <- c .: "capacity" case tryCommunalTable capacity of Nothing -> fail "Expected a natural number." Just t -> return $ JSONTable t _ -> fail "Expected exactly one of singleTable or communalTable." parseJSON _ = fail "Expected an object."
I could probably have done this more succinctly if I'd spent even more time on it than I already did, but it gets the job done and demonstrates the point. Instead of relying on run-time Reflection, the FromJSON instance is, unsurprisingly, a parser, composed from Aeson's specialised parser combinator API.
Since both serialisation and deserialization is based on string values, you should write automated tests that verify that the code works.
Apart from module declaration and imports etc. this hand-written JSON capability requires 27 lines of code. Can we do better with static types and Generics?
JSON serialisation based on types #
The intent with the Aeson library is that you define a type (a Data Transfer Object (DTO) if you will), and then let 'compiler magic' do the rest. In Haskell, it's not run-time Reflection, but a compilation technology called Generics. As I understand it, it automatically 'writes' the serialization and parsing code and turns it into machine code as part of normal compilation.
You're supposed to first turn on the
{-# LANGUAGE DeriveGeneric #-}
language pragma and then tell the compiler to automatically derive Generic for the DTO in question. You'll see an example of that shortly.
It's a fairly flexible system that you can tweak in various ways, but if it's possible to do it directly with the above Table type, please leave a comment explaining how. I tried, but couldn't make it work. To be clear, I could make it serializable, but not to the above JSON format. After enough Aeson Whac-A-Mole I decided to change tactics.
In Code That Fits in Your Head I explain how you're usually better off separating the role of serialization from the role of Domain Model. The way to do that is exactly by defining a DTO for serialisation, and let the Domain Model remain exclusively to model the rules of the application. The above Table type plays the latter role, so we need new DTO types.
We may start with the building blocks:
newtype CommunalDTO = CommunalDTO { communalCapacity :: Integer } deriving (Eq, Show, Generic)
Notice how it declaratively derives Generic, which works because of the DeriveGeneric language pragma.
From here, in principle, all that you need is just a single declaration to make it serializable:
instance ToJSON CommunalDTO
While it does serialize to JSON, it doesn't have the right format:
{ "communalCapacity": 42 }
The property name should be capacity, not communalCapacity. Why did I call the record field communalCapacity instead of capacity? Can't I just fix my CommunalDTO record?
Unfortunately, I can't just do that, because I also need a capacity JSON property for the single-table case, and Haskell isn't happy about duplicated field names in the same module. (This language feature truly is one of the weak points of Haskell.)
Instead, I can tweak the Aeson rules by supplying an Options value to the instance definition:
communalJSONOptions :: Options communalJSONOptions = defaultOptions { fieldLabelModifier = \s -> case s of "communalCapacity" -> "capacity" _ -> s } instance ToJSON CommunalDTO where toJSON = genericToJSON communalJSONOptions toEncoding = genericToEncoding communalJSONOptions
This instructs the compiler to modify how it generates the serialization code, and the generated JSON fragment is now correct.
We can do the same with the single-table case:
data SingleDTO = SingleDTO { singleCapacity :: Integer , minimalReservation :: Integer } deriving (Eq, Show, Generic) singleJSONOptions :: Options singleJSONOptions = defaultOptions { fieldLabelModifier = \s -> case s of "singleCapacity" -> "capacity" "minimalReservation" -> "minimalReservation" _ -> s } instance ToJSON SingleDTO where toJSON = genericToJSON singleJSONOptions toEncoding = genericToEncoding singleJSONOptions
This takes care of that case, but we still need a container type that will hold either one or the other:
data TableDTO = TableDTO { singleTable :: Maybe SingleDTO , communalTable :: Maybe CommunalDTO } deriving (Eq, Show, Generic) tableJSONOptions :: Options tableJSONOptions = defaultOptions { omitNothingFields = True } instance ToJSON TableDTO where toJSON = genericToJSON tableJSONOptions toEncoding = genericToEncoding tableJSONOptions
One way to model a sum type with a DTO is to declare both cases as Maybe fields. While it does allow illegal states to be representable (i.e. both kinds of tables defined at the same time, or none of them present) this is only par for the course at the application boundary.
That's quite a bit of infrastructure to stand up, but at least most of it can be reused for parsing.
JSON deserialisation based on types #
To allow parsing of JSON into the above DTO we can make them all FromJSON instances, e.g.:
instance FromJSON CommunalDTO where parseJSON = genericParseJSON communalJSONOptions
Notice that you can reuse the same communalJSONOptions used for the ToJSON instance. Repeat that exercise for the two other record types.
That's only half the battle, though, since this only gives you a way to parse and serialize the DTO. What you ultimately want is to persist or dehydrate Table data.
Converting DTO to Domain Model, and vice versa #
As usual, converting a nice, encapsulated value to a more relaxed format is safe and trivial:
toTableDTO :: Table -> TableDTO toTableDTO (Single (SingleT (N c) (N m))) = TableDTO (Just (SingleDTO c m)) Nothing toTableDTO (Communal (N c)) = TableDTO Nothing (Just (CommunalDTO c))
Going the other way is fundamentally a parsing exercise:
tryParseTable :: TableDTO -> Maybe Table tryParseTable (TableDTO (Just (SingleDTO c m)) Nothing) = trySingleTable c m tryParseTable (TableDTO Nothing (Just (CommunalDTO c))) = tryCommunalTable c tryParseTable _ = Nothing
Such an operation may fail, so the result is a Maybe Table. It could also have been an Either something Table, if you wanted to return information about errors when things go wrong. It makes the code marginally more complex, but doesn't change the overall thrust of this exploration.
Let's take stock of the type-based alternative. It requires 62 lines of code, distributed over three DTO types, their Options, their ToJSON and FromJSON instances, and finally the two conversions tryParseTable and toTableDTO.
Conclusion #
In this article I've explored two alternatives for converting a well-encapsulated Domain Model to and from JSON. One option is to directly manipulate the DOM. Another option is take a more declarative approach and define types that model the shape of the JSON data, and then leverage type-based automation (here, Generics) to automatically produce the code that parses and writes the JSON.
I've deliberately chosen a Domain Model with some constraints, in order to demonstrate how persisting a non-trivial data model might work. With that setup, writing 'loosely coupled' code directly against the DOM requires 27 lines of code, while 'taking advantage' of type-based automation requires 62 lines of code.
To be fair, the dice don't always land that way. You can't infer a general rule from a single example, and it's possible that I could have done something clever with Aeson to reduce the code. Even so, I think that there's a conclusion to be drawn, and it's this:
Type-based automation (Generics, or run-time Reflection) may seem simple at first glance. Just declare a type and let some automation library do the rest. It may happen, however, that you need to tweak the defaults so much that it would be easier skipping the type-based approach and instead directly manipulating the DOM.
I love static type systems, but I'm also watchful of their limitations. There's likely to be an inflection point where, on the one side, a type-based declarative API is best, while on the other side of that point, a more 'lightweight' approach is better.
The position of such an inflection point will vary from context to context. Just be aware of the possibility, and explore alternatives if things begin to feel awkward.
Serialization with and without Reflection
An investigation of alternatives.
I recently wrote a tweet that caused more responses than usual:
"A decade ago, I used .NET Reflection so often that I know most the the API by heart.
"Since then, I've learned better ways to solve my problems. I can't remember when was the last time I used .NET Reflection. I never need it.
"Do you?"
Most people who read my tweets are programmers, and some are, perhaps, not entirely neurotypical, but I intended the last paragraph to be a rhetorical question. My point, really, was to point out that if I tell you it's possible to do without Reflection, one or two readers might keep that in mind and at least explore options the next time the urge to use Reflection arises.
A common response was that Reflection is useful for (de)serialization of data. These days, the most common case is going to and from JSON, but the problem is similar if the format is XML, CSV, or another format. In a sense, even reading to and from a database is a kind of serialization.
In this little series of articles, I'm going to explore some alternatives to Reflection. I'll use the same example throughout, and I'll stick to JSON, but you can easily extrapolate to other serialization formats.
Table layouts #
As always, I find the example domain of online restaurant reservation systems to be so rich as to furnish a useful example. Imagine a multi-tenant service that enables restaurants to take and manage reservations.
When a new reservation request arrives, the system has to make a decision on whether to accept or reject the request. The layout, or configuration, of tables plays a role in that decision.
Such a multi-tenant system may have an API for configuring the restaurant; essentially, entering data into the system about the size and policies regarding tables in a particular restaurant.
Most restaurants have 'normal' tables where, if you reserve a table for three, you'll have the entire table for a duration. Some restaurants also have one or more communal tables, typically bar seating where you may get a view of the kitchen. Quite a few high-end restaurants have tables like these, because it enables them to cater to single diners without reserving an entire table that could instead have served two paying customers.

In Copenhagen, on the other hand, it's also not uncommon to have a special room for larger parties. I think this has something to do with the general age of the buildings in the city. Most establishments are situated in older buildings, with all the trappings, including load-bearing walls, cellars, etc. As part of a restaurant's location, there may be a big cellar room, second-story room, or other room that's not practical for the daily operation of the place, but which works for parties of, say, 15-30 people. Such 'private dining' rooms can be used for private occasions or company outings.
A maître d'hôtel may wish to configure the system with a variety of tables, including communal tables, and private dining tables as described above.
One way to model such requirements is to distinguish between two kinds of tables: Communal tables, and 'single' tables, and where single tables come with an additional property that models the minimal reservation required to reserve that table. A JSON representation might look like this:
{
"singleTable": {
"capacity": 16,
"minimalReservation": 10
}
}
This may represent a private dining table that seats up to sixteen people, and where the maître d'hôtel has decided to only accept reservations for at least ten guests.
A singleTable can also be used to model 'normal' tables without special limits. If the restaurant has a table for four, but is ready to accept a reservation for one person, you can configure a table for four, with a minimum reservation of one.
Communal tables are different, though:
{ "communalTable": { "capacity": 10 } }
Why not just model that as ten single tables that each seat one?
You don't want to do that because you want to make sure that parties can eat together. Some restaurants have more than one communal table. Imagine that you only have two communal tables of ten seats each. What happens if you model this as twenty single-person tables?
If you do that, you may accept reservations for parties of six, six, and six, because 6 + 6 + 6 = 18 < 20. When those three groups arrive, however, you discover that you have to split one of the parties! The party getting separated may not like that at all, and you are, after all, in the hospitality business.
Exploration #
In each article in this short series, I'll explore serialization with and without Reflection in a few languages. I'll start with Haskell, since that language doesn't have run-time Reflection. It does have a related facility called generics, not to be confused with .NET or Java generics, which in Haskell are called parametric polymorphism. It's confusing, I know.
Haskell generics look a bit like .NET Reflection, and there's some overlap, but it's not quite the same. The main difference is that Haskell generic programming all 'resolves' at compile time, so there's no run-time Reflection in Haskell.
If you don't care about Haskell, you can skip that article.
- Serializing restaurant tables in Haskell
- Serializing restaurant tables in F#
- Serializing restaurant tables in C#
As you can see, the next article repeats the exercise in F#, and if you also don't care about that language, you can skip that article as well.
The C# article, on the other hand, should be readable to not only C# programmers, but also developers who work in sufficiently equivalent languages.
Descriptive, not prescriptive #
The purpose of this article series is only to showcase alternatives. Based on the reactions my tweet elicited I take it that some people can't imagine how serialisation might look without Reflection.
It is not my intent that you should eschew the Reflection-based APIs available in your languages. In .NET, for example, a framework like ASP.NET MVC expects you to model JSON or XML as Data Transfer Objects. This gives you an illusion of static types at the boundary.
Even a Haskell web library like Servant expects you to model web APIs with static types.
When working with such a framework, it doesn't always pay to fight against its paradigm. When I work with ASP.NET, I define DTOs just like everyone else. On the other hand, if communicating with a backend system, I sometimes choose to skip static types and instead working directly with a JSON Document Object Model (DOM).
I occasionally find that it better fits my use case, but it's not the majority of times.
Conclusion #
While some sort of Reflection or metadata-driven mechanism is often used to implement serialisation, it often turns out that such convenient language capabilities are programmed on top of an ordinary object model. Even isolated to .NET, I think I'm on my third JSON library, and most (all?) turned out to have an underlying DOM that you can manipulate.
In this article I've set the stage for exploring how serialisation can work, with or (mostly) without Reflection.
If you're interested in the philosophy of science and epistemology, you may have noticed a recurring discussion in academia: A wider society benefits not only from learning what works, but also from learning what doesn't work. It would be useful if researchers published their failures along with their successes, yet few do (for fairly obvious reasons).
Well, I depend neither on research grants nor salary, so I'm free to publish negative results, such as they are.
Not that I want to go so far as to categorize what I present in the present articles as useless, but they're probably best applied in special circumstances. On the other hand, I don't know your context, and perhaps you're doing something I can't even imagine, and what I present here is just what you need.
Synchronizing concurrent teams
Or, rather: Try not to.
A few months ago I visited a customer and as the day was winding down we got to talk more informally. One of the architects mentioned, in an almost off-hand manner, "we've embarked on a SAFe journey..."
"Yes..?" I responded, hoping that my inflection would sound enough like a question that he'd elaborate.
Unfortunately, I'm apparently sometimes too subtle when dealing with people face-to-face, so I never got to hear just how that 'SAFe journey' was going. Instead, the conversation shifted to the adjacent topic of how to coordinate independent teams.
I told them that, in my opinion, the best way to coordinate independent teams is to not coordinate them. I don't remember exactly how I proceeded from there, but I probably said something along the lines that I consider coordination meetings between teams to be an 'architecture smell'. That the need to talk to other teams was a symptom that teams were too tightly coupled.
I don't remember if I said exactly that, but it would have been in character.
The architect responded: "I don't like silos."
How do you respond to that?
Autonomous teams #
I couldn't very well respond that silos are great. First, it doesn't sound very convincing. Second, it'd be an argument suitable only in a kindergarten. Are not! -Are too! -Not! -Too! etc.
After feeling momentarily checked, for once I managed to think on my feet, so I replied, "I don't suggest that your teams should be isolated from each other. I do encourage people to talk to each other, but I don't think that teams should coordinate much. Rather, think of each team as an organism on the savannah. They interact, and what they do impact others, but in the end they're autonomous life forms. I believe an architect's job is like a ranger's. You can't control the plants or animals, but you can nurture the ecosystem, herding it in a beneficial direction."

That ranger metaphor is an old pet peeve of mine, originating from what I consider one of my most under-appreciated articles: Zookeepers must become Rangers. It's closely related to the more popular metaphor of software architecture as gardening, but I like the wildlife variation because it emphasizes an even more hands-off approach. It removes the illusion that you can control a fundamentally unpredictable process, but replaces it with the hopeful emphasis on stewardship.
How do ecosystems thrive? A software architect (or ranger) should nurture resilience in each subsystem, just like evolution has promoted plants' and animals' ability to survive a variety of unforeseen circumstances: Flood, draught, fire, predators, lack of prey, disease, etc.
You want teams to work independently. This doesn't mean that they work in isolation, but rather they they are free to act according to their abilities and understanding of the situation. An architect can help them understand the wider ecosystem and predict tomorrow's weather, so to speak, but the team should remain autonomous.
Concurrent work #
I'm assuming that an organisation has multiple teams because they're supposed to work concurrently. While team A is off doing one thing, team B is doing something else. You can attempt to herd them in the same general direction, but beware of tight coordination.
What's the problem with coordination? Isn't it a kind of collaboration? Don't we consider that beneficial?
I'm not arguing that teams should be antagonistic. Like all metaphors, we should be careful not to take the savannah metaphor too far. I'm not imagining that one team consists of lions, apex predators, killing and devouring other teams.
Rather, the reason I'm wary of coordination is because it seems synonymous with synchronisation.
In Code That Fits in Your Head I've already discussed how good practices for Continuous Integration are similar to earlier lessons about optimistic concurrency. It recently struck me that we can draw a similar parallel between concurrent team work and parallel computing.
For decades we've known that the less synchronization, the faster parallel code is. Synchronization is costly.
In team work, coordination is like thread synchronization. Instead of doing work, you stop in order to coordinate. This implies that one thread or team has to wait for the other to catch up.
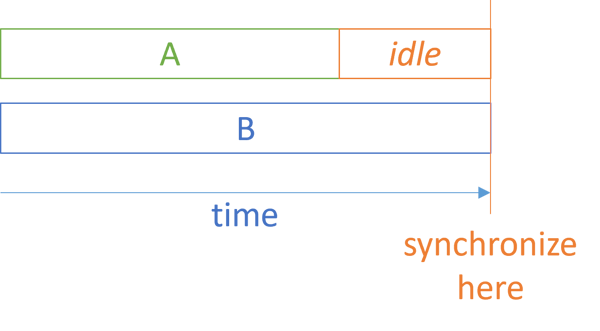
Unless work is perfectly evenly divided, team A may finish before team B. In order to coordinate, team A must sit idle for a while, waiting for B to catch up. (In development organizations, idleness is rarely allowed, so in practice, team A embarks on some other work, with consequences that I've already outlined.)
If you have more than two teams, this phenomenon only becomes worse. You'll have more idle time. This reminds me of Amdahl's law, which briefly put expresses that there's a limit to how much of a speed improvement you can get from concurrent work. The limit is related to the percentage of the work that can not be parallelized. The greater the need to synchronize work, the lower the ceiling. Conversely, the more you can let concurrent processes run without coordination, the more you gain from parallelization.
It seems to me that there's a direct counterpart in team organization. The more teams need to coordinate, the less is gained from having multiple teams.
But really, Fred Brooks could you have told you so in 1975.
Versioning #
A small development team may organize work informally. Work may be divided along 'natural' lines, each developer taking on tasks best suited to his or her abilities. If working in a code base with shared ownership, one developer doesn't have to wait on the work done by another developer. Instead, a programmer may complete the required work individually, or working together with a colleague. Coordination happens, but is both informal and frequent.
As development organizations grow, teams are formed. Separate teams are supposed to work independently, but may in practice often depend on each other. Team A may need team B to make a change before they can proceed with their own work. The (felt) need to coordinate team activities arise.
In my experience, this happens for a number of reasons. One is that teams may be divided along wrong lines; this is a socio-technical problem. Another, more technical, reason is that zookeepers rarely think explicitly about versioning or avoiding breaking changes. Imagine that team A needs team B to develop a new capability. This new capability implies a breaking change, so the teams will now need to coordinate.
Instead, team B should develop the new feature in such a way that it doesn't break existing clients. If all else fails, the new feature must exist side-by-side with the old way of doing things. With Continuous Deployment the new feature becomes available when it's ready. Team A still has to wait for the feature to become available, but no synchronization is required.
Conclusion #
Yet another lesson about thread-safety and concurrent transactions seems to apply to people and processes. Parallel processes should be autonomous, with as little synchronization as possible. The more you coordinate development teams, the more you limit the speed of overall work. This seems to suggest that something akin to Amdahl's law also applies to development organizations.
Instead of coordinating teams, encourage them to exist as autonomous entities, but set things up so that not breaking compatibility is a major goal for each team.
Trimming a Fake Object
A refactoring example.
When I introduce the Fake Object testing pattern to people, a common concern is the maintenance burden of it. The point of the pattern is that you write some 'working' code only for test purposes. At a glance, it seems as though it'd be more work than using a dynamic mock library like Moq or Mockito.
This article isn't really about that, but the benefit of a Fake Object is that it has a lower maintenance footprint because it gives you a single class to maintain when you change interfaces or base classes. Dynamic mock objects, on the contrary, leads to Shotgun surgery because every time you change an interface or base class, you have to revisit multiple tests.
In a recent article I presented a Fake Object that may have looked bigger than most people would find comfortable for test code. In this article I discuss how to trim it via a set of refactorings.
Original Fake read registry #
The article presented this FakeReadRegistry, repeated here for your convenience:
internal sealed class FakeReadRegistry : IReadRegistry { private readonly IReadOnlyCollection<Room> rooms; private readonly IDictionary<DateOnly, IReadOnlyCollection<Room>> views; public FakeReadRegistry(params Room[] rooms) { this.rooms = rooms; views = new Dictionary<DateOnly, IReadOnlyCollection<Room>>(); } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return EnumerateDates(arrival, departure) .Select(GetView) .Aggregate(rooms.AsEnumerable(), Enumerable.Intersect) .ToList(); } public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = QueryService.Reserve(booking, view); views[d] = newView; } } private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } } private IReadOnlyCollection<Room> GetView(DateOnly date) { if (views.TryGetValue(date, out var view)) return view; else return rooms; } }
This is 47 lines of code, spread over five members (including the constructor). Three of the methods have a cyclomatic complexity (CC) of 2, which is the maximum for this class. The remaining two have a CC of 1.
While you can play some CC golf with those CC-2 methods, that tends to pull the code in a direction of being less idiomatic. For that reason, I chose to present the code as above. Perhaps more importantly, it doesn't save that many lines of code.
Had this been a piece of production code, no-one would bat an eye at size or complexity, but this is test code. To add spite to injury, those 47 lines of code implement this two-method interface:
public interface IReadRegistry { IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure); void RoomBooked(Booking booking); }
Can we improve the situation?
Root cause analysis #
Before you rush to 'improve' code, it pays to understand why it looks the way it looks.
Code is a wonderfully malleable medium, so you should regard nothing as set in stone. On the other hand, there's often a reason it looks like it does. It may be that the previous programmers were incompetent ogres for hire, but often there's a better explanation.
I've outlined my thinking process in the previous article, and I'm not going to repeat it all here. To summarise, though, I've applied the Dependency Inversion Principle.
"clients [...] own the abstract interfaces"
In other words, I let the needs of the clients guide the design of the IReadRegistry interface, and then the implementation (FakeReadRegistry) had to conform.
But that's not the whole truth.
I was doing a programming exercise - the CQRS booking kata - and I was following the instructions given in the description. They quite explicitly outline the two dependencies and their methods.
When trying a new exercise, it's a good idea to follow instructions closely, so that's what I did. Once you get a sense of a kata, though, there's no law saying that you have to stick to the original rules. After all, the purpose of an exercise is to train, and in programming, trying new things is training.
Test code that wants to be production code #
A major benefit of test-driven development (TDD) is that it provides feedback. It pays to be tuned in to that channel. The above FakeReadRegistry seems to be trying to tell us something.
Consider the GetFreeRooms method. I'll repeat the single-expression body here for your convenience:
return EnumerateDates(arrival, departure)
.Select(GetView)
.Aggregate(rooms.AsEnumerable(), Enumerable.Intersect)
.ToList();
Why is that the implementation? Why does it need to first enumerate the dates in the requested interval? Why does it need to call GetView for each date?
Why don't I just do the following and be done with it?
internal sealed class FakeStorage : Collection<Booking>, IWriteRegistry, IReadRegistry { private readonly IReadOnlyCollection<Room> rooms; public FakeStorage(params Room[] rooms) { this.rooms = rooms; } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { var booked = this.Where(b => b.Overlaps(arrival, departure)).ToList(); return rooms .Where(r => !booked.Any(b => b.RoomName == r.Name)) .ToList(); } public void Save(Booking booking) { Add(booking); } }
To be honest, that's what I did first.
While there are two interfaces, there's only one Fake Object implementing both. That's often an easy way to address the Interface Segregation Principle and still keeping the Fake Object simple.
This is much simpler than FakeReadRegistry, so why didn't I just keep that?
I didn't feel it was an honest attempt at CQRS. In CQRS you typically write the data changes to one system, and then you have another logical process that propagates the information about the data modification to the read subsystem. There's none of that here. Instead of being based on one or more 'materialised views', the query is just that: A query.
That was what I attempted to address with FakeReadRegistry, and I think it's a much more faithful CQRS implementation. It's also more complex, as CQRS tends to be.
In both cases, however, it seems that there's some production logic trapped in the test code. Shouldn't EnumerateDates be production code? And how about the general 'algorithm' of RoomBooked:
- Enumerate the relevant dates
- Get the 'materialised' view for each date
- Calculate the new view for that date
- Update the collection of views for that date
That seems like just enough code to warrant moving it to the production code.
A word of caution before we proceed. When deciding to pull some of that test code into the production code, I'm making a decision about architecture.
Until now, I'd been following the Dependency Inversion Principle closely. The interfaces exist because the client code needs them. Those interfaces could be implemented in various ways: You could use a relational database, a document database, files, blobs, etc.
Once I decide to pull the above algorithm into the production code, I'm choosing a particular persistent data structure. This now locks the data storage system into a design where there's a persistent view per date, and another database of bookings.
Now that I'd learned some more about the exercise, I felt confident making that decision.
Template Method #
The first move I made was to create a superclass so that I could employ the Template Method pattern:
public abstract class ReadRegistry : IReadRegistry { public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return EnumerateDates(arrival, departure) .Select(GetView) .Aggregate(Rooms.AsEnumerable(), Enumerable.Intersect) .ToList(); } public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = QueryService.Reserve(booking, view); UpdateView(d, newView); } } protected abstract void UpdateView(DateOnly date, IReadOnlyCollection<Room> view); protected abstract IReadOnlyCollection<Room> Rooms { get; } protected abstract bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view); private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } } private IReadOnlyCollection<Room> GetView(DateOnly date) { if (TryGetView(date, out var view)) return view; else return Rooms; } }
This looks similar to FakeReadRegistry, so how is this an improvement?
The new ReadRegistry class is production code. It can, and should, be tested. (Due to the history of how we got here, it's already covered by tests, so I'm not going to repeat that effort here.)
True to the Template Method pattern, three abstract members await a child class' implementation. These are the UpdateView and TryGetView methods, as well as the Rooms read-only property (glorified getter method).
Imagine that in the production code, these are implemented based on file/document/blob storage - one per date. TryGetView would attempt to read the document from storage, UpdateView would create or modify the document, while Rooms returns a default set of rooms.
A Test Double, however, can still use an in-memory dictionary:
internal sealed class FakeReadRegistry : ReadRegistry { private readonly IReadOnlyCollection<Room> rooms; private readonly IDictionary<DateOnly, IReadOnlyCollection<Room>> views; protected override IReadOnlyCollection<Room> Rooms => rooms; public FakeReadRegistry(params Room[] rooms) { this.rooms = rooms; views = new Dictionary<DateOnly, IReadOnlyCollection<Room>>(); } protected override void UpdateView(DateOnly date, IReadOnlyCollection<Room> view) { views[date] = view; } protected override bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view) { return views.TryGetValue(date, out view); } }
Each override is a one-liner with cyclomatic complexity 1.
First round of clean-up #
An abstract class is already a polymorphic object, so we no longer need the IReadRegistry interface. Delete that, and update all code accordingly. Particularly, the QueryService now depends on ReadRegistry rather than IReadRegistry:
private readonly ReadRegistry readRegistry; public QueryService(ReadRegistry readRegistry) { this.readRegistry = readRegistry; }
Now move the Reserve function from QueryService to ReadRegistry. Once this is done, the QueryService looks like this:
public sealed class QueryService { private readonly ReadRegistry readRegistry; public QueryService(ReadRegistry readRegistry) { this.readRegistry = readRegistry; } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return readRegistry.GetFreeRooms(arrival, departure); } }
That class is only passing method calls along, so clearly no longer serving any purpose. Delete it.
This is a not uncommon in CQRS. One might even argue that if CQRS is done right, there's almost no code on the query side, since all the data view update happens as events propagate.
From abstract class to Dependency Injection #
While the current state of the code is based on an abstract base class, the overall architecture of the system doesn't hinge on inheritance. From Abstract class isomorphism we know that it's possible to refactor an abstract class to Constructor Injection. Let's do that.
First add an IViewStorage interface that mirrors the three abstract methods defined by ReadRegistry:
public interface IViewStorage { IReadOnlyCollection<Room> Rooms { get; } void UpdateView(DateOnly date, IReadOnlyCollection<Room> view); bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view); }
Then implement it with a Fake Object:
public sealed class FakeViewStorage : IViewStorage { private readonly IDictionary<DateOnly, IReadOnlyCollection<Room>> views; public IReadOnlyCollection<Room> Rooms { get; } public FakeViewStorage(params Room[] rooms) { Rooms = rooms; views = new Dictionary<DateOnly, IReadOnlyCollection<Room>>(); } public void UpdateView(DateOnly date, IReadOnlyCollection<Room> view) { views[date] = view; } public bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view) { return views.TryGetValue(date, out view); } }
Notice the similarity to FakeReadRegistry, which we'll get rid of shortly.
Now inject IViewStorage into ReadRegistry, and make ReadRegistry a regular (sealed) class:
public sealed class ReadRegistry { private readonly IViewStorage viewStorage; public ReadRegistry(IViewStorage viewStorage) { this.viewStorage = viewStorage; } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return EnumerateDates(arrival, departure) .Select(GetView) .Aggregate(viewStorage.Rooms.AsEnumerable(), Enumerable.Intersect) .ToList(); } public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = Reserve(booking, view); viewStorage.UpdateView(d, newView); } } public static IReadOnlyCollection<Room> Reserve( Booking booking, IReadOnlyCollection<Room> existingView) { return existingView .Where(r => r.Name != booking.RoomName) .ToList(); } private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } } private IReadOnlyCollection<Room> GetView(DateOnly date) { if (viewStorage.TryGetView(date, out var view)) return view; else return viewStorage.Rooms; } }
You can now delete the FakeReadRegistry Test Double, since FakeViewStorage has now taken its place.
Finally, we may consider if we can make FakeViewStorage even slimmer. While I usually favour composition over inheritance, I've found that deriving Fake Objects from collection base classes is often an efficient way to get a lot of mileage out of a few lines of code. FakeReadRegistry, however, had to inherit from ReadRegistry, so it couldn't derive from any other class.
FakeViewStorage isn't constrained in that way, so it's free to inherit from Dictionary<DateOnly, IReadOnlyCollection<Room>>:
public sealed class FakeViewStorage : Dictionary<DateOnly, IReadOnlyCollection<Room>>, IViewStorage { public IReadOnlyCollection<Room> Rooms { get; } public FakeViewStorage(params Room[] rooms) { Rooms = rooms; } public void UpdateView(DateOnly date, IReadOnlyCollection<Room> view) { this[date] = view; } public bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view) { return TryGetValue(date, out view); } }
This last move isn't strictly necessary, but I found it worth at least mentioning.
I hope you'll agree that this is a Fake Object that looks maintainable.
Conclusion #
Test-driven development is a feedback mechanism. If something is difficult to test, it tells you something about your System Under Test (SUT). If your test code looks bloated, that tells you something too. Perhaps part of the test code really belongs in the production code.
In this article, we started with a Fake Object that looked like it contained too much production code. Via a series of refactorings I moved the relevant parts to the production code, leaving me with a more idiomatic and conforming implementation.
CC golf
Noun. Game in which the goal is to minimise cyclomatic complexity.
Cyclomatic complexity (CC) is a rare code metric since it can be actually useful. In general, it's a good idea to minimise it as much as possible.
In short, CC measures looping and branching in code, and this is often where bugs lurk. While it's only a rough measure, I nonetheless find the metric useful as a general guideline. Lower is better.
Golf #
I'd like to propose the term "CC golf" for the activity of minimising cyclomatic complexity in an area of code. The name derives from code golf, in which you have to implement some behaviour (typically an algorithm) in fewest possible characters.
Such games can be useful because they enable you to explore different ways to express yourself in code. It's always a good kata constraint. The first time I tried that was in 2011, and when looking back on that code today, I'm not that impressed. Still, it taught me a valuable lesson about the Visitor pattern that I never forgot, and that later enabled me to connect some important dots.
But don't limit CC golf to katas and the like. Try it in your production code too. Most production code I've seen could benefit from some CC golf, and if you use Git tactically you can always stash the changes if they're no good.
Idiomatic tension #
Alternative expressions with lower cyclomatic complexity may not always be idiomatic. Let's look at a few examples. In my previous article, I listed some test code where some helper methods had a CC of 2. Here's one of them:
private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } }
Can you express this functionality with a CC of 1? In Haskell it's essentially built in as (. pred) . enumFromTo, and in F# it's also idiomatic, although more verbose:
let enumerateDates (arrival : DateOnly) departure = Seq.initInfinite id |> Seq.map arrival.AddDays |> Seq.takeWhile (fun d -> d < departure)
Can we do the same in C#?
If there's a general API in .NET that corresponds to the F#-specific Seq.initInfinite I haven't found it, but we can do something like this:
private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { const int infinity = int.MaxValue; // As close as int gets, at least return Enumerable.Range(0, infinity).Select(arrival.AddDays).TakeWhile(d => d < departure); }
In C# infinite sequences are generally unusual, but if you were to create one, a combination of while true and yield return would be the most idiomatic. The problem with that, though, is that such a construct has a cyclomatic complexity of 2.
The above suggestion gets around that problem by pretending that int.MaxValue is infinity. Practically, at least, a 32-bit signed integer can't get larger than that anyway. I haven't tried to let F#'s Seq.initInfinite run out, but by its type it seems int-bound as well, so in practice it, too, probably isn't infinite. (Or, if it is, the index that it supplies will have to overflow and wrap around to a negative value.)
Is this alternative C# code better than the first? You be the judge of that. It has a lower cyclomatic complexity, but is less idiomatic. This isn't uncommon. In languages with a procedural background, there's often tension between lower cyclomatic complexity and how 'things are usually done'.
Checking for null #
Is there a way to reduce the cyclomatic complexity of the GetView helper method?
private IReadOnlyCollection<Room> GetView(DateOnly date) { if (views.TryGetValue(date, out var view)) return view; else return rooms; }
This is an example of the built-in API being in the way. In F#, you naturally write the same behaviour with a CC of 1:
let getView (date : DateOnly) =
views |> Map.tryFind date |> Option.defaultValue rooms |> Set.ofSeq
That TryGet idiom is in the way for further CC reduction, it seems. It is possible to reach a CC of 1, though, but it's neither pretty nor idiomatic:
private IReadOnlyCollection<Room> GetView(DateOnly date) { views.TryGetValue(date, out var view); return new[] { view, rooms }.Where(x => x is { }).First()!; }
Perhaps there's a better way, but if so, it escapes me. Here, I use my knowledge that view is going to remain null if TryGetValue doesn't find the dictionary entry. Thus, I can put it in front of an array where I put the fallback value rooms as the second element. Then I filter the array by only keeping the elements that are not null (that's what the x is { } pun means; I usually read it as x is something). Finally, I return the first of these elements.
I know that rooms is never null, but apparently the compiler can't tell. Thus, I have to suppress its anxiety with the ! operator, telling it that this will result in a non-null value.
I would never use such a code construct in a professional C# code base.
Side effects #
The third helper method suggests another kind of problem that you may run into:
public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = QueryService.Reserve(booking, view); views[d] = newView; } }
Here the higher-than-one CC stems from the need to loop through dates in order to produce a side effect for each. Even in F# I do that:
member this.RoomBooked booking = for d in enumerateDates booking.Arrival booking.Departure do let newView = getView d |> QueryService.reserve booking |> Seq.toList views <- Map.add d newView views
This also has a cyclomatic complexity of 2. You could do something like this:
member this.RoomBooked booking = enumerateDates booking.Arrival booking.Departure |> Seq.iter (fun d -> let newView = getView d |> QueryService.reserve booking |> Seq.toList in views <- Map.add d newView views)
but while that nominally has a CC of 1, it has the same level of indentation as the previous attempt. This seems to indicate, at least, that it doesn't really address any complexity issue.
You could also try something like this:
member this.RoomBooked booking = enumerateDates booking.Arrival booking.Departure |> Seq.map (fun d -> d, getView d |> QueryService.reserve booking |> Seq.toList) |> Seq.iter (fun (d, newView) -> views <- Map.add d newView views)
which, again, may be nominally better, but forced me to wrap the map output in a tuple so that both d and newView is available to Seq.iter. I tend to regard that as a code smell.
This latter version is, however, fairly easily translated to C#:
public void RoomBooked(Booking booking) { EnumerateDates(booking.Arrival, booking.Departure) .Select(d => (d, view: QueryService.Reserve(booking, GetView(d)))) .ToList() .ForEach(x => views[x.d] = x.view); }
The standard .NET API doesn't have something equivalent to Seq.iter (although you could trivially write such an action), but you can convert any sequence to a List<T> and use its ForEach method.
In practice, though, I tend to agree with Eric Lippert. There's already an idiomatic way to iterate over each item in a collection, and being explicit is generally helpful to the reader.
Church encoding #
There's a general solution to most of CC golf: Whenever you need to make a decision and branch between two or more pathways, you can model that with a sum type. In C# you can mechanically model that with Church encoding or the Visitor pattern. If you haven't tried that, I recommend it for the exercise, but once you've done it enough times, you realise that it requires little creativity.
As an example, in 2021 I revisited the Tennis kata with the explicit purpose of translating my usual F# approach to the exercise to C# using Church encoding and the Visitor pattern.
Once you've got a sense for how Church encoding enables you to simulate pattern matching in C#, there are few surprises. You may also rightfully question what is gained from such an exercise:
public IScore VisitPoints(IPoint playerOnePoint, IPoint playerTwoPoint) { return playerWhoWinsBall.Match( playerOne: playerOnePoint.Match<IScore>( love: new Points(new Fifteen(), playerTwoPoint), fifteen: new Points(new Thirty(), playerTwoPoint), thirty: new Forty(playerWhoWinsBall, playerTwoPoint)), playerTwo: playerTwoPoint.Match<IScore>( love: new Points(playerOnePoint, new Fifteen()), fifteen: new Points(playerOnePoint, new Thirty()), thirty: new Forty(playerWhoWinsBall, playerOnePoint))); }
Believe it or not, but that method has a CC of 1 despite the double indentation strongly suggesting that there's some branching going on. To a degree, this also highlights the limitations of the cyclomatic complexity metric. Conversely, stupidly simple code may have a high CC rating.
Most of the examples in this article border on the pathological, and I don't recommend that you write code like that. I recommend that you do the exercise. In less pathological scenarios, there are real benefits to be reaped.
Idioms #
In 2015 I published an article titled Idiomatic or idiosyncratic? In it, I tried to explore the idea that the notion of idiomatic code can sometimes hold you back. I revisited that idea in 2021 in an article called Against consistency. The point in both cases is that just because something looks unfamiliar, it doesn't mean that it's bad.
Coding idioms somehow arose. If you believe that there's a portion of natural selection involved in the development of coding idioms, you may assume by default that idioms represent good ways of doing things.
To a degree I believe this to be true. Many idioms represent the best way of doing things at the time they settled into the shape that we now know them. Languages and contexts change, however. Just look at the many approaches to data lookups there have been over the years. For many years now, C# has settled into the so-called TryParse idiom to solve that problem. In my opinion this represents a local maximum.
Languages that provide Maybe (AKA option) and Either (AKA Result) types offer a superior alternative. These types naturally compose into CC 1 pipelines, whereas TryParse requires you to stop what you're doing in order to check a return value. How very C-like.
All that said, I still think you should write idiomatic code by default, but don't be a slave by what's considered idiomatic, just as you shouldn't be a slave to consistency. If there's a better way of doing things, choose the better way.
Conclusion #
While cyclomatic complexity is a rough measure, it's one of the few useful programming metrics I know of. It should be as low as possible.
Most professional code I encounter implements decisions almost exclusively with language primitives: if, for, switch, while, etc. Once, an organisation hired me to give a one-day anti-if workshop. There are other ways to make decisions in code. Most of those alternatives reduce cyclomatic complexity.
That's not really a goal by itself, but reducing cyclomatic complexity tends to produce the beneficial side effect of structuring the code in a more sustainable way. It becomes easier to understand and change.
As the cliché goes: Choose the right tool for the job. You can't, however, do that if you have nothing to choose from. If you only know of one way to do a thing, you have no choice.
Play a little CC golf with your code from time to time. It may improve the code, or it may not. If it didn't, just stash those changes. Either way, you've probably learned something.
Fakes are Test Doubles with contracts
Contracts of Fake Objects can be described by properties.
The first time I tried my hand with the CQRS Booking kata, I abandoned it after 45 minutes because I found that I had little to learn from it. After all, I've already done umpteen variations of (restaurant) booking code examples, in several programming languages. The code example that accompanies my book Code That Fits in Your Head is only the largest and most complete of those.
I also wrote an MSDN Magazine article in 2011 about CQRS, so I think I have that angle covered as well.
Still, while at first glance the kata seemed to have little to offer me, I've found myself coming back to it a few times. It does enable me to focus on something else than the 'production code'. In fact, it turns out that even if (or perhaps particularly when) you use test-driven development (TDD), there's precious little production code. Let's get that out of the way first.
Production code #
The few times I've now done the kata, there's almost no 'production code'. The implied CommandService has two lines of effective code:
public sealed class CommandService { private readonly IWriteRegistry writeRegistry; private readonly IReadRegistry readRegistry; public CommandService(IWriteRegistry writeRegistry, IReadRegistry readRegistry) { this.writeRegistry = writeRegistry; this.readRegistry = readRegistry; } public void BookARoom(Booking booking) { writeRegistry.Save(booking); readRegistry.RoomBooked(booking); } }
The QueryService class isn't much more exciting:
public sealed class QueryService { private readonly IReadRegistry readRegistry; public QueryService(IReadRegistry readRegistry) { this.readRegistry = readRegistry; } public static IReadOnlyCollection<Room> Reserve( Booking booking, IReadOnlyCollection<Room> existingView) { return existingView.Where(r => r.Name != booking.RoomName).ToList(); } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return readRegistry.GetFreeRooms(arrival, departure); } }
The kata only suggests the GetFreeRooms method, which is only a single line. The only reason the Reserve function also exists is to pull a bit of testable logic back from the below Fake object. I'll return to that shortly.
I've also done the exercise in F#, essentially porting the C# implementation, which only highlights how simple it all is:
module CommandService = let bookARoom (writeRegistry : IWriteRegistry) (readRegistry : IReadRegistry) booking = writeRegistry.Save booking readRegistry.RoomBooked booking module QueryService = let reserve booking existingView = existingView |> Seq.filter (fun r -> r.Name <> booking.RoomName) let getFreeRooms (readRegistry : IReadRegistry) arrival departure = readRegistry.GetFreeRooms arrival departure
That's both the Command side and the Query side!
This represents my honest interpretation of the kata. Really, there's nothing to it.
The reason I still find the exercise interesting is that it explores other aspects of TDD than most katas. The most common katas require you to write a little algorithm: Bowling, Word wrap, Roman Numerals, Diamond, Tennis, etc.
The CQRS Booking kata suggests no interesting algorithm, but rather teaches some important lessons about software architecture, separation of concerns, and, if you approach it with TDD, real-world test automation. In contrast to all those algorithmic exercises, this one strongly suggests the use of Test Doubles.
Fakes #
You could attempt the kata with a dynamic 'mocking' library such as Moq or Mockito, but I haven't tried. Since Stubs and Mocks break encapsulation I favour Fake Objects instead.
Creating a Fake write registry is trivial:
internal sealed class FakeWriteRegistry : Collection<Booking>, IWriteRegistry { public void Save(Booking booking) { Add(booking); } }
Its counterpart, the Fake read registry, turns out to be much more involved:
internal sealed class FakeReadRegistry : IReadRegistry { private readonly IReadOnlyCollection<Room> rooms; private readonly IDictionary<DateOnly, IReadOnlyCollection<Room>> views; public FakeReadRegistry(params Room[] rooms) { this.rooms = rooms; views = new Dictionary<DateOnly, IReadOnlyCollection<Room>>(); } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return EnumerateDates(arrival, departure) .Select(GetView) .Aggregate(rooms.AsEnumerable(), Enumerable.Intersect) .ToList(); } public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = QueryService.Reserve(booking, view); views[d] = newView; } } private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } } private IReadOnlyCollection<Room> GetView(DateOnly date) { if (views.TryGetValue(date, out var view)) return view; else return rooms; } }
I think I can predict the most common reaction: That's much more code than the System Under Test! Indeed. For this particular exercise, this may indicate that a 'dynamic mock' library may have been a better choice. I do, however, also think that it's an artefact of the kata description's lack of requirements.
As is evident from the restaurant sample code that accompanies Code That Fits in Your Head, once you add realistic business rules the production code grows, and the ratio of test code to production code becomes better balanced.
The size of the FakeReadRegistry class also stems from the way the .NET base class library API is designed. The GetView helper method demonstrates that it requires four lines of code to look up an entry in a dictionary but return a default value if the entry isn't found. That's a one-liner in F#:
let getView (date : DateOnly) = views |> Map.tryFind date |> Option.defaultValue rooms |> Set.ofSeq
I'll show the entire F# Fake later, but you could also play some CC golf with the C# code. That's a bit besides the point, though.
Command service design #
Why does FakeReadRegistry look like it does? It's a combination of the kata description and my prior experience with CQRS. When adopting an asynchronous message-based architecture, I would usually not implement the write side exactly like that. Notice how the CommandService class' BookARoom method seems to repeat itself:
public void BookARoom(Booking booking) { writeRegistry.Save(booking); readRegistry.RoomBooked(booking); }
While semantically it seems to be making two different statements, structurally they're identical. If you rename the methods, you could wrap both method calls in a single Composite. In a more typical CQRS architecture, you'd post a Command on bus:
public void BookARoom(Booking booking) { bus.BookRoom(booking); }
This makes that particular BookARoom method, and perhaps the entire CommandService class, look redundant. Why do we need it?
As presented here, we don't, but in a real application, the Command service would likely perform some pre- and post-processing. For example, if this was a web application, the Command service might instead be a Controller concerned with validating and translating HTTP- or Web-based input to a Domain Object before posting to the bus.
A realistic code base would also be asynchronous, which, on .NET, would imply the use of the async and await keywords, etc.
Read registry design #
A central point of CQRS is that you can optimise the read side for the specific tasks that it needs to perform. Instead of performing a dynamic query every time a client requests a view, you can update and persist a view. Imagine having a JSON or HTML file that the system can serve upon request.
Part of handling a Command or Event is that the system background processes update persistent views once per event.
For the particular hotel booking system, I imagine that the read registry has a set of files, blobs, documents, or denormalised database rows. When it receives notification of a booking, it'll need to remove that room from the dates of the booking.
While a booking may stretch over several days, I found it simplest to think of the storage system as subdivided into single dates, instead of ranges. Indeed, the GetFreeRooms method is a ranged query, so if you really wanted to denormalise the views, you could create a persistent view per range. This would, however, require that you precalculate and persist a view for October 2 to October 4, and another one for October 2 to October 5, and so on. The combinatorial explosion suggests that this isn't a good idea, so instead I imagine keeping a persistent view per date, and then perform a bit of on-the-fly calculation per query.
That's what FakeReadRegistry does. It also falls back to a default collection of rooms for all the dates that are yet untouched by a booking. This is, again, because I imagine that I might implement a real system like that.
You may still protest that the FakeReadRegistry duplicates production code. True, perhaps, but if this really is a concern, you could refactor it to the Template Method pattern.
Still, it's not really that complicated; it only looks that way because C# and the Dictionary API is too heavy on ceremony. The Fake looks much simpler in F#:
type FakeReadRegistry (rooms : IReadOnlyCollection<Room>) = let mutable views = Map.empty let enumerateDates (arrival : DateOnly) departure = Seq.initInfinite id |> Seq.map arrival.AddDays |> Seq.takeWhile (fun d -> d < departure) let getView (date : DateOnly) = views |> Map.tryFind date |> Option.defaultValue rooms |> Set.ofSeq interface IReadRegistry with member this.GetFreeRooms arrival departure = enumerateDates arrival departure |> Seq.map getView |> Seq.fold Set.intersect (Set.ofSeq rooms) |> Set.toList :> _ member this.RoomBooked booking = for d in enumerateDates booking.Arrival booking.Departure do let newView = getView d |> QueryService.reserve booking |> Seq.toList views <- Map.add d newView views
This isn't just more dense than the corresponding C# code, as F# tends to be, it also has a lower cyclomatic complexity. Both the EnumerateDates and GetView C# methods have a cyclomatic complexity of 2, while their F# counterparts rate only 1.
For production code, cyclomatic complexity of 2 is fine if the code is covered by automatic tests. In test code, however, we should be wary of any branching or looping, since there are (typically) no tests of the test code.
While I am going to show some tests of that code in what follows, I do that for a different reason.
Contract #
When explaining Fake Objects to people, I've begun to use a particular phrase:
A Fake Object is a polymorphic implementation of a dependency that fulfils the contract, but lacks some of the ilities.
It's funny how you can arrive at something that strikes you as profound, only to discover that it was part of the definition all along:
"We acquire or build a very lightweight implementation of the same functionality as provided by a component on which the SUT [System Under Test] depends and instruct the SUT to use it instead of the real DOC [Depended-On Component]. This implementation need not have any of the "-ilities" that the real DOC needs to have"
A common example is a Fake Repository object that pretends to be a database, often by leveraging a built-in collection API. The above FakeWriteRegistry is as simple an example as you could have. A slightly more compelling example is the FakeUserRepository shown in another article. Such an 'in-memory database' fulfils the implied contract, because if you 'save' something in the 'database' you can later retrieve it again with a query. As long as the object remains in memory.
The ilities that such a Fake database lacks are
- data persistence
- thread safety
- transaction support
and perhaps others. Such qualities are clearly required in a real production environment, but are in the way in an automated testing context. The implied contract, however, is satisfied: What you save you can later retrieve.
Now consider the IReadRegistry interface:
public interface IReadRegistry { IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure); void RoomBooked(Booking booking); }
Which contract does it imply, given what you know about the CQRS Booking kata?
I would suggest the following:
- Precondition:
arrivalshould be less than (or equal?) todeparture. - Postcondition:
GetFreeRoomsshould always return a result. Null isn't a valid return value. - Invariant: After calling
RoomBooked,GetFreeRoomsshould exclude that room when queried on overlapping dates.
There may be other parts of the contract than this, but I find the third one most interesting. This is exactly what you would expect from a real system: If you reserve a room, you'd be surprised to see GetFreeRooms indicating that this room is free if queried about dates that overlap the reservation.
This is the sort of implied interaction that Stubs and Mocks break, but that FakeReadRegistry guarantees.
Properties #
There's a close relationship between contracts and properties. Once you can list preconditions, invariants, and postconditions for an object, there's a good chance that you can write code that exercises those qualities. Indeed, why not use property-based testing to do so?
I don't wish to imply that you should (normally) write tests of your test code. The following rather serves as a concretisation of the notion that a Fake Object is a Test Double that implements the 'proper' behaviour. In the following, I'll subject the FakeReadRegistry class to that exercise. To do that, I'll use CsCheck 2.14.1 with xUnit.net 2.5.3.
Before tackling the above invariant, there's a simpler invariant specific to the FakeReadRegistry class. A FakeReadRegistry object takes a collection of rooms via its constructor, so for this particular implementation, we may wish to establish the reasonable invariant that GetFreeRooms doesn't 'invent' rooms on its own:
private static Gen<Room> GenRoom => from name in Gen.String select new Room(name); [Fact] public void GetFreeRooms() { (from rooms in GenRoom.ArrayUnique from arrival in Gen.Date.Select(DateOnly.FromDateTime) from i in Gen.Int[1, 1_000] let departure = arrival.AddDays(i) select (rooms, arrival, departure)) .Sample((rooms, arrival, departure) => { var sut = new FakeReadRegistry(rooms); var actual = sut.GetFreeRooms(arrival, departure); Assert.Subset(new HashSet<Room>(rooms), new HashSet<Room>(actual)); }); }
This property asserts that the actual value returned from GetFreeRooms is a subset of the rooms used to initialise the sut. Recall that the subset relation is reflexive; i.e. a set is a subset of itself.
The same property written in F# with Hedgehog 0.13.0 and Unquote 6.1.0 may look like this:
module Gen = let room = Gen.alphaNum |> Gen.array (Range.linear 1 10) |> Gen.map (fun chars -> { Name = String chars }) let dateOnly = let min = DateOnly(2000, 1, 1).DayNumber let max = DateOnly(2100, 1, 1).DayNumber Range.linear min max |> Gen.int32 |> Gen.map DateOnly.FromDayNumber [<Fact>] let GetFreeRooms () = Property.check <| property { let! rooms = Gen.room |> Gen.list (Range.linear 0 100) let! arrival = Gen.dateOnly let! i = Gen.int32 (Range.linear 1 1_000) let departure = arrival.AddDays i let sut = FakeReadRegistry rooms :> IReadRegistry let actual = sut.GetFreeRooms arrival departure test <@ Set.isSubset (Set.ofSeq rooms) (Set.ofSeq actual) @> }
Simpler syntax, same idea.
Likewise, we can express the contract that describes the relationship between RoomBooked and GetFreeRooms like this:
[Fact] public void RoomBooked() { (from rooms in GenRoom.ArrayUnique.Nonempty from arrival in Gen.Date.Select(DateOnly.FromDateTime) from i in Gen.Int[1, 1_000] let departure = arrival.AddDays(i) from room in Gen.OneOfConst(rooms) from id in Gen.Guid let booking = new Booking(id, room.Name, arrival, departure) select (rooms, booking)) .Sample((rooms, booking) => { var sut = new FakeReadRegistry(rooms); sut.RoomBooked(booking); var actual = sut.GetFreeRooms(booking.Arrival, booking.Departure); Assert.DoesNotContain(booking.RoomName, actual.Select(r => r.Name)); }); }
or, in F#:
[<Fact>] let RoomBooked () = Property.check <| property { let! rooms = Gen.room |> Gen.list (Range.linear 1 100) let! arrival = Gen.dateOnly let! i = Gen.int32 (Range.linear 1 1_000) let departure = arrival.AddDays i let! room = Gen.item rooms let! id = Gen.guid let booking = { ClientId = id RoomName = room.Name Arrival = arrival Departure = departure } let sut = FakeReadRegistry rooms :> IReadRegistry sut.RoomBooked booking let actual = sut.GetFreeRooms arrival departure test <@ not (Seq.contains room actual) @> }
In both cases, the property books a room and then proceeds to query GetFreeRooms to see which rooms are free. Since the query is exactly in the range from booking.Arrival to booking.Departure, we expect not to see the name of the booked room among the free rooms.
(As I'm writing this, I think that there may be a subtle bug in the F# property. Can you spot it?)
Conclusion #
A Fake Object isn't like other Test Doubles. While Stubs and Mocks break encapsulation, a Fake Object not only stays encapsulated, but it also fulfils the contract implied by a polymorphic API (interface or base class).
Or, put another way: When is a Fake Object the right Test Double? When you can describe the contract of the dependency.
But if you can't describe the contract of a dependency, you should seriously consider if the design is right.
A C# port of validation with partial round trip
A raw port of the previous F# demo code.
This article is part of a short article series on applicative validation with a twist. The twist is that validation, when it fails, should return not only a list of error messages; it should also retain that part of the input that was valid.
In the previous article I showed F# demo code, and since the original forum question that prompted the article series was about F# code, for a long time, I left it there.
Recently, however, I've found myself writing about validation in a broader context:
- An applicative reservation validation example in C#
- ASP.NET validation revisited
- Can types replace validation?
- Validation and business rules
- Validating or verifying emails
Perhaps I should consider adding a validation tag to the blog...
In that light I thought that it might be illustrative to continue this article series with a port to C#.
Here, I use techniques already described on this site to perform the translation. Follow the links for details.
The translation given here is direct so produces some fairly non-idiomatic C# code.
Building blocks #
The original problem is succinctly stated, and I follow it as closely as possible. This includes potential errors that may be present in the original post.
The task is to translate some input to a Domain Model with good encapsulation. The input type looks like this, translated to a C# record:
public sealed record Input(string? Name, DateTime? DoB, string? Address)
Notice that every input may be null. This indicates poor encapsulation, but is symptomatic of most input. At the boundaries, static types are illusory. Perhaps it would have been more idiomatic to model such input as a Data Transfer Object, but it makes little difference to what comes next.
I consider validation a solved problem, because it's possible to model the process as an applicative functor. Really, validation is a parsing problem.
Since my main intent with this article is to demonstrate a technique, I will allow myself a few shortcuts. Like I did when I first encountered the Args kata, I start by copying the Validated code from An applicative reservation validation example in C#; you can go there if you're interested in it. I'm not going to repeat it here.
The target type looks similar to the above Input record, but doesn't allow null values:
public sealed record ValidInput(string Name, DateTime DoB, string Address);
This could also have been a 'proper' class. The following code doesn't depend on that.
Validating names #
Since I'm now working in an ostensibly object-oriented language, I can make the various validation functions methods on the Input record. Since I'm treating validation as a parsing problem, I'm going to name those methods with the TryParse prefix:
private Validated<(Func<Input, Input>, IReadOnlyCollection<string>), string> TryParseName() { if (Name is null) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), string>( (x => x, new[] { "name is required" })); if (Name.Length <= 3) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), string>( (i => i with { Name = null }, new[] { "no bob and toms allowed" })); return Validated.Succeed<(Func<Input, Input>, IReadOnlyCollection<string>), string>(Name); }
As the two previous articles have explained, the result of trying to parse input is a type isomorphic to Either, but here called Validated<F, S>. (The reason for this distinction is that we don't want the monadic behaviour of Either, because monads short-circuit.)
When parsing succeeds, the TryParseName method returns the Name wrapped in a Success case.
Parsing the name may fail in two different ways. If the name is missing, the method returns the input and the error message "name is required". If the name is present, but too short, TryParseName returns another error message, and also resets Name to null.
Compare the C# code with the corresponding F# or Haskell code and notice how much more verbose the C# has to be.
While it's possible to translate many functional programming concepts to a language like C#, syntax does matter, because it affects readability.
Validating date of birth #
From here, the port is direct, if awkward. Here's how to validate the date-of-birth field:
private Validated<(Func<Input, Input>, IReadOnlyCollection<string>), DateTime> TryParseDoB(DateTime now) { if (!DoB.HasValue) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), DateTime>( (x => x, new[] { "dob is required" })); if (DoB.Value <= now.AddYears(-12)) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), DateTime>( (i => i with { DoB = null }, new[] { "get off my lawn" })); return Validated.Succeed<(Func<Input, Input>, IReadOnlyCollection<string>), DateTime>( DoB.Value); }
I suspect that the age check should really have been a greater-than relation, but I'm only reproducing the original code.
Validating addresses #
The final building block is to parse the input address:
private Validated<(Func<Input, Input>, IReadOnlyCollection<string>), string> TryParseAddress() { if (Address is null) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), string>( (x => x, new[] { "add1 is required" })); return Validated.Succeed<(Func<Input, Input>, IReadOnlyCollection<string>), string>( Address); }
The TryParseAddress only checks whether or not the Address field is present.
Composition #
The above methods are private because the entire problem is simple enough that I can test the composition as a whole. Had I wanted to, however, I could easily have made them public and tested them individually.
You can now use applicative composition to produce a single validation method:
public Validated<(Input, IReadOnlyCollection<string>), ValidInput> TryParse(DateTime now) { var name = TryParseName(); var dob = TryParseDoB(now); var address = TryParseAddress(); Func<string, DateTime, string, ValidInput> createValid = (n, d, a) => new ValidInput(n, d, a); static (Func<Input, Input>, IReadOnlyCollection<string>) combineErrors( (Func<Input, Input> f, IReadOnlyCollection<string> es) x, (Func<Input, Input> g, IReadOnlyCollection<string> es) y) { return (z => y.g(x.f(z)), y.es.Concat(x.es).ToArray()); } return createValid .Apply(name, combineErrors) .Apply(dob, combineErrors) .Apply(address, combineErrors) .SelectFailure(x => (x.Item1(this), x.Item2)); }
This is where the Validated API is still awkward. You need to explicitly define a function to compose error cases. In this case, combineErrors composes the endomorphisms and concatenates the collections.
The final step 'runs' the endomorphism. x.Item1 is the endomorphism, and this is the Input value being validated. Again, this isn't readable in C#, but it's where the endomorphism removes the invalid values from the input.
Tests #
Since applicative validation is a functional technique, it's intrinsically testable.
Testing a successful validation is as easy as this:
[Fact] public void ValidationSucceeds() { var now = DateTime.Now; var eightYearsAgo = now.AddYears(-8); var input = new Input("Alice", eightYearsAgo, "x"); var actual = input.TryParse(now); var expected = Validated.Succeed<(Input, IReadOnlyCollection<string>), ValidInput>( new ValidInput("Alice", eightYearsAgo, "x")); Assert.Equal(expected, actual); }
As is often the case, the error conditions are more numerous, or more interesting, if you will, than the success case, so this requires a parametrised test:
[Theory, ClassData(typeof(ValidationFailureTestCases))] public void ValidationFails( Input input, Input expected, IReadOnlyCollection<string> expectedMessages) { var now = DateTime.Now; var actual = input.TryParse(now); var (inp, msgs) = Assert.Single(actual.Match( onFailure: x => new[] { x }, onSuccess: _ => Array.Empty<(Input, IReadOnlyCollection<string>)>())); Assert.Equal(expected, inp); Assert.Equal(expectedMessages, msgs); }
I also had to take actual apart in order to inspects its individual elements. When working with a pure and immutable data structure, I consider that a test smell. Rather, one should be able to use structural equality for better tests. Unfortunately, .NET collections don't have structural equality, so the test has to pull the message collection out of actual in order to verify it.
Again, in F# or Haskell you don't have that problem, and the tests are much more succinct and robust.
The test cases are implemented by this nested ValidationFailureTestCases class:
private class ValidationFailureTestCases : TheoryData<Input, Input, IReadOnlyCollection<string>> { public ValidationFailureTestCases() { Add(new Input(null, null, null), new Input(null, null, null), new[] { "add1 is required", "dob is required", "name is required" }); Add(new Input("Bob", null, null), new Input(null, null, null), new[] { "add1 is required", "dob is required", "no bob and toms allowed" }); Add(new Input("Alice", null, null), new Input("Alice", null, null), new[] { "add1 is required", "dob is required" }); var eightYearsAgo = DateTime.Now.AddYears(-8); Add(new Input("Alice", eightYearsAgo, null), new Input("Alice", eightYearsAgo, null), new[] { "add1 is required" }); var fortyYearsAgo = DateTime.Now.AddYears(-40); Add(new Input("Alice", fortyYearsAgo, "x"), new Input("Alice", null, "x"), new[] { "get off my lawn" }); Add(new Input("Tom", fortyYearsAgo, "x"), new Input(null, null, "x"), new[] { "get off my lawn", "no bob and toms allowed" }); Add(new Input("Tom", eightYearsAgo, "x"), new Input(null, eightYearsAgo, "x"), new[] { "no bob and toms allowed" }); } }
All eight tests pass.
Conclusion #
Once you know how to model sum types (discriminated unions) in C#, translating something like applicative validation isn't difficult per se. It's a fairly automatic process.
The code is hardly idiomatic C#, and the type annotations are particularly annoying. Things work as expected though, and it isn't difficult to imagine how one could refactor some of this code to a more idiomatic form.
Domain Model first
Persistence concerns second.
A few weeks ago, I published an article with the title Do ORMs reduce the need for mapping? Not surprisingly, this elicited more than one reaction. In this article, I'll respond to a particular kind of reaction.
First, however, I'd like to reiterate the message of the previous article, which is almost revealed by the title: Do object-relational mappers (ORMs) reduce the need for mapping? To which the article answers a tentative no.
Do pay attention to the question. It doesn't ask whether ORMs are bad in general, or in all cases. It mainly analyses whether the use of ORMs reduces the need to write code that maps between different representations of data: From database to objects, from objects to Data Transfer Objects (DTOs), etc.
Granted, the article looks at a wider context, which I think is only a responsible thing to do. This could lead some readers to extrapolate from the article's specific focus to draw a wider conclusion.
Encapsulation-first #
Most of the systems I work with aren't CRUD systems, but rather systems where correctness is important. As an example, one of my clients does security-heavy digital infrastructure. Earlier in my career, I helped write web shops when these kinds of systems were new. Let me tell you: System owners were quite concerned that prices were correct, and that orders were taken and handled without error.
In my book Code That Fits in Your Head I've tried to capture the essence of those kinds of system with the accompanying sample code, which pretends to be an online restaurant reservation system. While this may sound like a trivial CRUD system, the business logic isn't entirely straightforward.
The point I was making in the previous article is that I consider encapsulation to be more important than 'easy' persistence. I don't mind writing a bit of mapping code, since typing isn't a programming bottleneck anyway.
When prioritising encapsulation you should be able to make use of any design pattern, run-time assertion, as well as static type systems (if you're working in such a language) to guard correctness. You should be able to compose objects, define Value Objects, wrap single values to avoid primitive obsession, make constructors private, leverage polymorphism and effectively use any trick your language, idiom, and platform has on offer. If you want to use Church encoding or the Visitor pattern to represent a sum type, you should be able to do that.
When writing these kinds of systems, I start with the Domain Model without any thought of how to persist or retrieve data.
In my experience, once the Domain Model starts to congeal, the persistence question tends to answer itself. There's usually one or two obvious ways to store and read data.
Usually, a relational database isn't the most obvious choice.
Persistence ignorance #
Write the best API you can to solve the problem, and then figure out how to store data. This is the allegedly elusive ideal of persistence ignorance, which turns out to be easier than rumour has it, once you cast a wider net than relational databases.
It seems to me, though, that more than one person who has commented on my previous article have a hard time considering alternatives. And granted, I've consulted with clients who knew how to operate a particular database system, but nothing else, and who didn't want to consider adopting another technology. I do understand that such constraints are real, too. Thus, if you need to compromise for reasons such as these, you aren't doing anything wrong. You may still, however, try to get the best out of the situation.
One client of mine, for example, didn't want to operate anything else than SQL Server, which they already know. For an asynchronous message-based system, then, we chose NServiceBus and configured it to use SQL Server as a persistent queue.
Several comments still seem to assume that persistence must look in a particular way.
"So having a Order, OrderLine, Person, Address and City, all the rows needed to be loaded in advance, mapped to objects and references set to create the object graph to be able to, say, display shipping costs based on person's address."
I don't wish to single out Vlad, but this is both the first comment, and it captures the essence of other comments well. I imagine that what he has in mind is something like this:
I've probably simplified things a bit too much. In a more realistic model, each person may have a collection of addresses, instead of just one. If so, it only strengthens Vlad's point, because that would imply even more tables to read.
The unstated assumption, however, is that a fully normalised relational data model is the correct way to store such data.
It's not. As I already mentioned, I spent the first four years of my programming career developing web shops. Orders were an integral part of that work.
An order is a document. You don't want the customer's address to be updatable after the fact. With a normalised relational model, if you change the customer's address row in the future, it's going to look as though the order went to that address instead of the address it actually went to.
This also explains why the order lines should not point to the actually product entries in the product catalogue. Trust me, I almost shipped such a system once, when I was young and inexperienced.
You should, at the very least, denormalise the database model. To a degree, this has already happened here, since the implied order has order lines, that, I hope, are copies of the relevant product data, rather than linked to the product catalogue.
Such insights, however, suggest that other storage mechanisms may be more appropriate.
Putting that aside for a moment, though, how would a persistence-ignorant Domain Model look?
I'd probably start with something like this:
var order = new Order( new Person("Olive", "Hoyle", new Address("Green Street 15", new City("Oakville"), "90125")), new OrderLine(123, 1), new OrderLine(456, 3), new OrderLine(789, 2));
(As the ZIP code implies, I'm more of a Yes fan, but still can't help but relish writing new Order in code.)
With code like this, many a DDD'er would start talking about Aggregate Roots, but that is, frankly, a concept that never made much sense to me. Rather, the above order is a tree composed of immutable data structures.
It trivially serializes to e.g. JSON:
{
"customer": {
"firstName": "Olive",
"lastName": "Hoyle",
"address": {
"street": "Green Street 15",
"city": { "name": "Oakville" },
"zipCode": "90125"
}
},
"orderLines": [
{
"sku": 123,
"quantity": 1
},
{
"sku": 456,
"quantity": 3
},
{
"sku": 789,
"quantity": 2
}
]
}
All of this strongly suggests that this kind of data would be much easier to store and retrieve with a document database instead of a relational database.
While that's just one example, it strikes me as a common theme when discussing persistence. For most online transaction processing systems, relational database aren't necessarily the best fit.
The cart before the horse #
Another comment also starts with the premise that a data model is fundamentally relational. This one purports to model the relationship between sheikhs, their wives, and supercars. While I understand that the example is supposed to be tongue-in-cheek, the comment launches straight into problems with how to read and persist such data without relying on an ORM.
Again, I don't intend to point fingers at anyone, but on the other hand, I can't suggest alternatives when a problem is presented like that.
The whole point of developing a Domain Model first is to find a good way to represent the business problem in a way that encourages correctness and ease of use.
If you present me with a relational model without describing the business goals you're trying to achieve, I don't have much to work with.
It may be that your business problem is truly relational, in which case an ORM probably is a good solution. I wrote as much in the previous article.
In many cases, however, it looks to me as though programmers start with a relational model, only to proceed to complain that it's difficult to work with in object-oriented (or functional) code.
If you, on the other hand, start with the business problem and figure out how to model it in code, the best way to store the data may suggest itself. Document databases are often a good fit, as are event stores. I've never had need for a graph database, but perhaps that would be a better fit for the sheikh domain suggested by qfilip.
Reporting #
While I no longer feel that relational databases are particularly well-suited for online transaction processing, they are really good at one thing: Ad-hoc querying. Because it's such a rich and mature type of technology, and because SQL is a powerful language, you can slice and dice data in multiple ways.
This makes relational databases useful for reporting and other kinds of data extraction tasks.
You may have business stakeholders who insist on a relational database for that particular reason. It may even be a good reason.
If, however, the sole purpose of having a relational database is to support reporting, you may consider setting it up as a secondary system. Keep your online transactional data in another system, but regularly synchronize it to a relational database. If the only purpose of the relational database is to support reporting, you can treat it as a read-only system. This makes synchronization manageable. In general, you should avoid two-way synchronization if at all possible, but one-way synchronization is usually less of a problem.
Isn't that going to be more work, or more expensive?
That question, again, has no single answer. Of course setting up and maintaining two systems is more work at the outset. On the other hand, there's a perpetual cost to be paid if you come up with the wrong architecture. If development is slow, and you have many bugs in production, or similar problems, the cause could be that you've chosen the wrong architecture and you're now fighting a losing battle.
On the other hand, if you relegate relational databases exclusively to a reporting role, chances are that there's a lot of off-the-shelf software that can support your business users. Perhaps you can even hire a paratechnical power user to take care of that part of the system, freeing you to focus on the 'actual' system.
All of this is only meant as inspiration. If you don't want to, or can't, do it that way, then this article doesn't help you.
Conclusion #
When discussing databases, and particularly ORMs, some people approach the topic with the unspoken assumption that a relational database is the only option for storing data. Many programmers are so skilled in relational data design that they naturally use those skills when thinking new problems over.
Sometimes problems are just relational in nature, and that's fine. More often than not, however, that's not the case.
Try to model a business problem without concern for storage and see where that leads you. Test-driven development is often a great technique for such a task. Then, once you have a good API, consider how to store the data. The Domain Model that you develop in that way may naturally suggest a good way to store and retrieve the data.
Comments
Again, I don't intend to point fingers at anyone, but on the other hand, I can't suggest alternatives when a problem is presented like that.
Heh, that's fair criticism, not finger pointing. I wanted to give a better example here, but I gave up halfway through writing it. You raised some good points. I'll have to rethink my approach on domain modeling further, before asking any meaningful questions.
Years of working with EF-Core in a specific way got me... indoctrinated. Not all things are bad ofcourse, but I have missed the bigger picture in some areas, as far as I can tell.
Thanks for dedicating so many articles to the subject.
At the boundaries, static types are illusory
Static types are useful, but have limitations.
Regular readers of this blog may have noticed that I like static type systems. Not the kind of static types offered by C, which strikes me as mostly being able to distinguish between way too many types of integers and pointers. A good type system is more than just numbers on steroids. A type system like C#'s is workable, but verbose. The kind of type system I find most useful is when it has algebraic data types and good type inference. The examples that I know best are the type systems of F# and Haskell.
As great as static type systems can be, they have limitations. Hillel Wayne has already outlined one kind of distinction, but here I'd like to focus on another constraint.
Application boundaries #
Any piece of software interacts with the 'rest of the world'; effectively everything outside its own process. Sometimes (but increasingly rarely) such interaction is exclusively by way of some user interface, but more and more, an application interacts with other software in some way.

Here I've drawn the application as an opaque disc in order to emphasise that what happens inside the process isn't pertinent to the following discussion. The diagram also includes some common kinds of traffic. Many applications rely on some kind of database or send messages (email, SMS, Commands, Events, etc.). We can think of such traffic as the interactions that the application initiates, but many systems also receive and react to incoming data: HTTP traffic or messages that arrive on a queue, and so on.
When I talk about application boundaries, I have in mind what goes on in that interface layer.
An application can talk to the outside world in multiple ways: It may read or write a file, access shared memory, call operating-system APIs, send or receive network packets, etc. Usually you get to program against higher-level abstractions, but ultimately the application is dealing with various binary protocols.
Protocols #
The bottom line is that at a sufficiently low level of abstraction, what goes in and out of your application has no static type stronger than an array of bytes.
You may counter-argue that higher-level APIs deal with that to present the input and output as static types. When you interact with a text file, you'll typically deal with a list of strings: One for each line in the file. Or you may manipulate JSON, XML, Protocol Buffers, or another wire format using a serializer/deserializer API. Sometime, as is often the case with CSV, you may need to write a very simple parser yourself. Or perhaps something slightly more involved.
To demonstrate what I mean, there's no shortage of APIs like JsonSerializer.Deserialize, which enables you to write code like this:
let n = JsonSerializer.Deserialize<Name> (json, opts)
and you may say: n is statically typed, and its type is Name! Hooray! But you do realise that that's only half a truth, don't you?
An interaction at the application boundary is expected to follow some kind of protocol. This is even true if you're reading a text file. In these modern times, you may expect a text file to contain Unicode, but have you ever received a file from a legacy system and have to deal with its EBCDIC encoding? Or an ASCII file with a code page different from the one you expect? Or even just a file written on a Unix system, if you're on Windows, or vice versa?
In order to correctly interpret or transmit such data, you need to follow a protocol.
Such a protocol can be low-level, as the character-encoding examples I just listed, but it may also be much more high-level. You may, for example, consider an HTTP request like this:
POST /restaurants/90125/reservations?sig=aco7VV%2Bh5sA3RBtrN8zI8Y9kLKGC60Gm3SioZGosXVE%3D HTTP/1.1
Content-Type: application/json
{
"at": "2021-12-08 20:30",
"email": "snomob@example.com",
"name": "Snow Moe Beal",
"quantity": 1
}
Such an interaction implies a protocol. Part of such a protocol is that the HTTP request's body is a valid JSON document, that it has an at property, that that property encodes a valid date and time, that quantity is a natural number, that email is present, and so on.
You can model the expected input as a Data Transfer Object (DTO):
public sealed class ReservationDto { public string? At { get; set; } public string? Email { get; set; } public string? Name { get; set; } public int Quantity { get; set; } }
and even set up your 'protocol handlers' (here, an ASP.NET Core action method) to use such a DTO:
public Task<ActionResult> Post(ReservationDto dto)
While this may look statically typed, it assumes a particular protocol. What happens when the bytes on the wire don't follow the protocol?
Well, we've already been around that block more than once.
The point is that there's always an implied protocol at the application boundary, and you can choose to model it more or less explicitly.
Types as short-hands for protocols #
In the above example, I've relied on some static typing to deal with the problem. After all, I did define a DTO to model the expected shape of input. I could have chosen other alternatives: Perhaps I could have used a JSON parser to explicitly use the JSON DOM, or even more low-level used Utf8JsonReader. Ultimately, I could have decided to write my own JSON parser.
I'd rarely (or never?) choose to implement a JSON parser from scratch, so that's not what I'm advocating. Rather, my point is that you can leverage existing APIs to deal with input and output, and some of those APIs offer a convincing illusion that what happens at the boundary is statically typed.
This illusion is partly API-specific, and partly language-specific. In .NET, for example, JsonSerializer.Deserialize looks like it'll always deserialize any JSON string into the desired model. Obviously, that's a lie, because the function will throw an exception if the operation is impossible (i.e. when the input is malformed). In .NET (and many other languages or platforms), you can't tell from an API's type what the failure modes might be. In contrast, aeson's fromJSON function returns a type that explicitly indicates that deserialization may fail. Even in Haskell, however, this is mostly an idiomatic convention, because Haskell also 'supports' exceptions.
At the boundary, a static type can be a useful shorthand for a protocol. You declare a static type (e.g. a DTO) and rely on built-in machinery to handle malformed input. You give up some fine-grained control in exchange for a more declarative model.
I often choose to do that because I find such a trade-off beneficial, but I'm under no illusion that my static types fully model what goes 'on the wire'.
Reversed roles #
So far, I've mostly discussed input validation. Can types replace validation? No, but they can make most common validation scenarios easier. What happens when you return data?
You may decide to return a statically typed value. A serializer can faithfully convert such a value to a proper wire format (JSON, XML, or similar). The recipient may not care about that type. After all, you may return a Haskell value, but the system receiving the data is written in Python. Or you return a C# object, but the recipient is JavaScript.
Should we conclude, then, that there's no reason to model return data with static types? Not at all, because by modelling output with static types, you are being conservative with what you send. Since static types are typically more rigid than 'just code', there may be corner cases that a type can't easily express. While this may pose a problem when it comes to input, it's only a benefit when it comes to output. This means that you're narrowing the output funnel and thus making your system easier to work with.

Now consider another role-reversal: When your application initiates an interaction, it starts by producing output and receives input as a result. This includes any database interaction. When you create, update, or delete a row in a database, you send data, and receive a response.
Should you not consider Postel's law in that case?

Most people don't, particularly if they rely on object-relational mappers (ORMs). After all, if you have a static type (class) that models a database row, what's the harm using that when updating the database?
Probably none. After all, based on what I've just written, using a static type is a good way to be conservative with what you send. Here's an example using Entity Framework:
using var db = new RestaurantsContext(ConnectionString); var dbReservation = new Reservation { PublicId = reservation.Id, RestaurantId = restaurantId, At = reservation.At, Name = reservation.Name.ToString(), Email = reservation.Email.ToString(), Quantity = reservation.Quantity }; await db.Reservations.AddAsync(dbReservation); await db.SaveChangesAsync();
Here we send a statically typed Reservation 'Entity' to the database, and since we use a static type, we're being conservative with what we send. That's only good.
What happens when we query a database? Here's a typical example:
public async Task<Restaurants.Reservation?> ReadReservation(int restaurantId, Guid id) { using var db = new RestaurantsContext(ConnectionString); var r = await db.Reservations.FirstOrDefaultAsync(x => x.PublicId == id); if (r is null) return null; return new Restaurants.Reservation( r.PublicId, r.At, new Email(r.Email), new Name(r.Name), r.Quantity); }
Here I read a database row r and unquestioning translate it to my domain model. Should I do that? What if the database schema has diverged from my application code?
I suspect that much grief and trouble with relational databases, and particularly with ORMs, stem from the illusion that an ORM 'Entity' is a statically-typed view of the database schema. Typically, you can either use an ORM like Entity Framework in a code-first or a database-first fashion, but regardless of what you choose, you have two competing 'truths' about the database: The database schema and the Entity Classes.
You need to be disciplined to keep those two views in synch, and I'm not asserting that it's impossible. I'm only suggesting that it may pay to explicitly acknowledge that static types may not represent any truth about what's actually on the other side of the application boundary.
Types are an illusion #
Given that I usually find myself firmly in the static-types-are-great camp, it may seem odd that I now spend an entire article trashing them. Perhaps it looks as though I've had a revelation and made an about-face, but that's not the case. Rather, I'm fond of making the implicit explicit. This often helps improve understanding, because it helps delineate conceptual boundaries.
This, too, is the case here. All models are wrong, but some models are useful. So are static types, I believe.
A static type system is a useful tool that enables you to model how your application should behave. The types don't really exist at run time. Even though .NET code (just to point out an example) compiles to a binary representation that includes type information, once it runs, it JITs to machine code. In the end, it's just registers and memory addresses, or, if you want to be even more nihilistic, electrons moving around on a circuit board.
Even at a higher level of abstraction, you may say: But at least, a static type system can help you encapsulate rules and assumptions. In a language like C#, for example, consider a predicative type like this NaturalNumber class:
public struct NaturalNumber : IEquatable<NaturalNumber> { private readonly int i; public NaturalNumber(int candidate) { if (candidate < 1) throw new ArgumentOutOfRangeException( nameof(candidate), $"The value must be a positive (non-zero) number, but was: {candidate}."); this.i = candidate; } // Various other members follow...
Such a class effectively protects the invariant that a natural number is always a positive integer. Yes, that works well until someone does this:
var n = (NaturalNumber)FormatterServices.GetUninitializedObject(typeof(NaturalNumber));
This n value has the internal value 0. Yes, FormatterServices.GetUninitializedObject bypasses the constructor. This thing is evil, but it exists, and at least in the current discussion serves to illustrate the point that types are illusions.
This isn't just a flaw in C#. Other languages have similar backdoors. One of the most famously statically-typed languages, Haskell, comes with unsafePerformIO, which enables you to pretend that nothing untoward is going on even if you've written some impure code.
You may (and should) institute policies to not use such backdoors in your normal code bases. You don't need them.
Types are useful models #
All this may seem like an argument that types are useless. That would, however, be to draw the wrong conclusion. Types don't exist at run time to the same degree that Python objects or JavaScript functions don't exist at run time. Any language (except assembler) is an abstraction: A way to model computer instructions so that programming becomes easier (one would hope, but then...). This is true even for C, as low-level and detail-oriented as it may seem.
If you grant that high-level programming languages (i.e. any language that is not machine code or assembler) are useful, you must also grant that you can't rule out the usefulness of types. Notice that this argument is one of logic, rather than of preference. The only claim I make here is that programming is based on useful illusions. That the abstractions are illusions don't prevent them from being useful.
In statically typed languages, we effectively need to pretend that the type system is good enough, strong enough, generally trustworthy enough that it's safe to ignore the underlying reality. We work with, if you will, a provisional truth that serves as a user interface to the computer.
Even though a computer program eventually executes on a processor where types don't exist, a good compiler can still check that our models look sensible. We say that it type-checks. I find that indispensable when modelling the internal behaviour of a program. Even in a large code base, a compiler can type-check whether all the various components look like they may compose correctly. That a program compiles is no guarantee that it works correctly, but if it doesn't type-check, it's strong evidence that the code's model is internally inconsistent.
In other words, that a statically-typed program type-checks is a necessary, but not a sufficient condition for it to work.
This holds as long as we're considering program internals. Some language platforms allow us to take this notion further, because we can link software components together and still type-check them. The .NET platform is a good example of this, since the IL code retains type information. This means that the C#, F#, or Visual Basic .NET compiler can type-check your code against the APIs exposed by external libraries.
On the other hand, you can't extend that line of reasoning to the boundary of an application. What happens at the boundary is ultimately untyped.
Are types useless at the boundary, then? Not at all. Alexis King has already dealt with this topic better than I could, but the point is that types remain an effective way to capture the result of parsing input. You can view receiving, handling, parsing, or validating input as implementing a protocol, as I've already discussed above. Such protocols are application-specific or domain-specific rather than general-purpose protocols, but they are still protocols.
When I decide to write input validation for my restaurant sample code base as a set of composable parsers, I'm implementing a protocol. My starting point isn't raw bits, but rather a loose static type: A DTO. In other cases, I may decide to use a different level of abstraction.
One of the (many) reasons I have for finding ORMs unhelpful is exactly because they insist on an illusion past its usefulness. Rather, I prefer implementing the protocol that talks to my database with a lower-level API, such as ADO.NET:
private static Reservation ReadReservationRow(SqlDataReader rdr) { return new Reservation( (Guid)rdr["PublicId"], (DateTime)rdr["At"], new Email((string)rdr["Email"]), new Name((string)rdr["Name"]), new NaturalNumber((int)rdr["Quantity"])); }
This actually isn't a particular good protocol implementation, because it fails to take Postel's law into account. Really, this code should be a Tolerant Reader. In practice, not that much input contravariance is possible, but perhaps, at least, this code ought to gracefully handle if the Name field was missing.
The point of this particular example isn't that it's perfect, because it's not, but rather that it's possible to drop down to a lower level of abstraction, and sometimes, this may be a more honest representation of reality.
Conclusion #
It may be helpful to acknowledge that static types don't really exist. Even so, internally in a code base, a static type system can be a powerful tool. A good type system enables a compiler to check whether various parts of your code looks internally consistent. Are you calling a procedure with the correct arguments? Have you implemented all methods defined by an interface? Have you handled all cases defined by a sum type? Have you correctly initialized an object?
As useful type systems are for this kind of work, you should also be aware of their limitations. A compiler can check whether a code base's internal model makes sense, but it can't verify what happens at run time.
As long as one part of your code base sends data to another part of your code base, your type system can still perform a helpful sanity check, but for data that enters (or leaves) your application at run time, bets are off. You may attempt to model what input should look like, and it may even be useful to do that, but it's important to acknowledge that reality may not look like your model.
You can write statically-typed, composable parsers. Some of them are quite elegant, but the good ones explicitly model that parsing of input is error-prone. When input is well-formed, the result may be a nicely encapsulated, statically-typed value, but when it's malformed, the result is one or more error values.
Perhaps the most important message is that databases, other web services, file systems, etc. involve input and output, too. Even if you write code that initiates a database query, or a web service request, should you implicitly trust the data that comes back?
This question of trust doesn't have to imply security concerns. Rather, systems evolve and errors happen. Every time you interact with an external system, there's a risk that it has become misaligned with yours. Static types can't protect you against that.

Comments
Haskell (the language) does not provide primitives to access to data representation per-se, during the compilation GHC (the compiler) erase a lot of information (more or less depending on the profiling flags) in order to provide to the run-time system (RTS) a minimal "bytecode".
That being said, provide three ways to deal structurally with values:
Template Haskell is low-level as it implies to deal with the AST, it is also harder to debug as, in order to be evaluated, the main compilation phase is stopped, then the Template Haskell code is ran, and finally the main compilation phase continue. It also causes compilation cache issues.
Generics take type's structure and generate a representation at type-level, the main idea is to be able to go back and forth between the type and its representation, so you can define so behavior over a structure, the good thing being that, since the representation is known at compile-time, many optimizations can be done. On complex types it tends to slow-down compilation and produce larger-than-usual binaries, it is generraly the way libraries are implemented.
Typeable is a purely value-level type representation, you get only on type whatever the type structure is, it is generally used when you have "dynamic" types, it provides safe ways to do coercion.
Haskell tends to push as much things as possible in compile-time, this may explain this tendency.
Thank you for writing. I was already aware of Template Haskell and Generics, but Typeable is new to me. I don't consider the first two equivalent to Reflection, since they resolve at compile time. They're more akin to automated code generation, I think. Reflection, as I'm used to it from .NET, is a run-time feature where you can inspect and interact with types and values as the code is executing.
I admit that I haven't had the time to more than browse the documentation of Typeable, and it's so abstract that it's not clear to me what it does, how it works, or whether it's actually comparable to Reflection. The first question that comes to my mind regards the type class
Typeableitself. It has no instances. Is it one of those special type classes (like Coercible) that one doesn't have to explicitly implement?I don't know the .NET ecosystem well, but I guess you can borrow information at run-time we have at compile-time with TemplateHaskell and Generics, I think you are right then.
You can derive
Typeableas any othe type classes:data MyType = MyType { myString :: String, myInt :: Int } deriving stock (Eq, Show, Typeable)It's pretty "low-level",
typeRepgives you aTypeRep a(abeing the type represented) which is a representation of the type with primitive elements (More details here).Then, you'll be able to either pattern match on it, or cast it (which it not like casting in Java for example, because you are just proving to the compiler that two types are equivalent).