ploeh blog danish software design
Some thoughts on naming tests
What is the purpose of a test name?
Years ago I was participating in a coding event where we did katas. My pairing partner and I was doing silent ping pong. Ping-pong style pair programming is when one programmer writes a test and passes the keyboard to the partner, who writes enough code to pass the test. He or she then writes a new test and passes control back to the first person. In the silent variety, you're not allowed to talk. This is an exercise in communicating via code.
My partner wrote a test and I made it pass. After the exercise was over, we were allowed to talk to evaluate how it went, and my partner remarked that he'd been surprised that I'd implemented the opposite behaviour of what he'd intended. (It was something where there was a fork in the logic depending on a number being less than or greater to zero; I don't recall the exact details.)
We looked at the test that he had written, and sure enough: He'd named the test by clearly indicating one behaviour, but then he'd written an assertion that looked for the opposite behaviour.
I hadn't even noticed.
I didn't read the test name. I only considered the test body, because that's the executable specification.
How tests are named #
I've been thinking about test names ever since. What is the role of a test name?
In some languages, you write unit tests as methods or functions. That's how you do it in C#, Java, and many other languages:
[Theory] [InlineData("Home")] [InlineData("Calendar")] [InlineData("Reservations")] public void WithControllerHandlesSuffix(string name) { var sut = new UrlBuilder(); var actual = sut.WithController(name + "Controller"); var expected = sut.WithController(name); Assert.Equal(expected, actual); }
Usually, when we define new class methods, we've learned that naming is important. Truly, this applies to test methods, too?
Yet, other languages don't use class methods to define tests. The most common JavaScript frameworks don't, and neither does Haskell HUnit. Instead, tests are simply values with labels.
This hints at something that may be important.
The role of test names #
If tests aren't necessarily class methods, then what role do names play?
Usually, when considering method names, it's important to provide a descriptive name in order to help client developers. A client developer writing calling code must figure out which methods to call on an object. Good names help with that.
Automated tests, on the other hand, have no explicit callers. There's no client developer to communicate with. Instead, a test framework such as xUnit.net scans the public API of a test suite and automatically finds the test methods to execute.
The most prominent motivation for writing good method names doesn't apply here. We must reevaluate the role of test names, also keeping in mind that with some frameworks, in some languages, tests aren't even methods.
Mere anarchy is loosed upon the world #
The story that introduces this article has a point. When considering a test, I tend to go straight to the test body. I only read the test name if I find the test body unclear.
Does this mean that the test name is irrelevant? Should we simply number the tests: Test1, Test212, and so on?
That hardly seems like a good idea - not even to a person like me who considers the test name secondary to the test definition.
This begs the question, though: If Test42 isn't a good name, then what does a good test name look like?
Naming schemes #
Various people suggest naming schemes. In the .NET world many people like Roy Osherove's naming standard for unit tests: [UnitOfWork_StateUnderTest_ExpectedBehavior]. I find it too verbose to my tastes, but my point isn't to attack this particular naming scheme. In my Types + Properties = Software article series, I experimented with using a poor man's version of Given When Then:
[<Property>] let ``Given deuce when player wins then score is correct`` (winner : Player) = let actual : Score = scoreWhenDeuce winner let expected = Advantage winner expected =! actual
It was a worthwhile experiment, but I don't think I ever used that style again. After all, Given When Then is just another way of saying Arrange Act Assert, and I already organise my test code according to the AAA pattern.
These days, I don't follow any particular naming scheme, but I do keep a guiding principle in mind.
Information channel #
A test name, whether it's a method name or a label, is an opportunity to communicate with the reader of the code. You can communicate via code, via names, via comments, and so on. A test name is more like a mandatory comment than a normal method name.
Books like Clean Code make a compelling case that comments should be secondary to good names. The point isn't that all comments are bad, but that some are:
var z = x + y; // Add x and y
It's rarely a good idea to add a comment that describes what the code does. This should already be clear from the code itself.
A comment can still provide important information that code can't easily do. It may explain the purpose of the code. I try to take this into account when naming tests: Not repeat what the code does, but suggest a hint about its raison d'être.
I try to strike a balance between Test2112 and Given deuce when player wins then score is correct. I view the task of naming tests as equivalent to producing section headings in an article like this one. They offer a hint at the kind of information that might be available in the section (The role of test names, How tests are named, or Information channel), but sometimes they're more tongue-in-cheek than helpful (Mere anarchy is loosed upon the world). I tend to name tests with a similar degree of precision (or lack thereof): HomeReturnsJson, NoHackingOfUrlsAllowed, GetPreviousYear, etcetera.
These names, in isolation, hardly tell you what the tests are about. I'm okay with that, because I don't think that they have to.
What do you use test names for? #
I occasionally discuss this question with other people. It seems to me that it's one of the topics where Socratic questioning breaks down:
Them: How do you name tests?
Me: I try to strike a balance between information and not repeating myself.
Them: How do you like this particular naming scheme?
Me: It looks verbose to me. It seems to be repeating what's already in the test code.
Them: I like to read the test name to see what the test does.
Me: If the name and test code disagree, which one is right?
Them: The test name should follow the naming scheme.
Me: Why do you find that important?
Them: It's got... electrolytes.
Okay, I admit that I'm a being uncharitable, but the point that I'm after is that test names are different, yet most people seem to reflect little on this.
When do you read test names?
Personally, I rarely read or otherwise use test names. When I'm writing a test, I also write the name, but at that point I don't really need the name. Sometimes I start with a placeholder name (Foo), write the test, and change the name once I understand what the test does.
Once a test is written, ideally it should just be sitting there as a regression test. The less you touch it, the better you can trust it.
You may have hundreds or thousands of tests. When you run your test suite, you care about the outcome. Did it pass or fail? The outcome is the result of a Boolean and operation. The test suite only passes when all tests pass, but you don't have to look at each test result. The aggregate result is enough as long as the test suite passes.
You only need to look at a test when it fails. When this happens, most tools enable you to go straight to the failing test by clicking on it. (And if this isn't possible, I usually find it easier to navigate to the failing test either by line number or by copying the test name and navigating to it by pasting the name into my editor's navigation UI.) You don't really need the name to find a failing test. If the test was named Test1337 it would be as easy to find as if it was named Given deuce when player wins then score is correct.
Once I look at a failing test, I start by looking at the test code and comparing that to the assertion message.
Usually, when a test fails, it breaks for a reason. A code change caused the test to fail. Often, the offending change was one you did ten seconds earlier. Armed with an assertion message and the test code, I usually understand the problem right away.
In rare cases the test is one that I've never seen before, and I'm confused about its purpose. This is when I read the test name. At that point, I appreciate if the name is helpful.
Conclusion #
I'm puzzled that people are so passionate about test names. I consider them the least important part of a test. A name isn't irrelevant, but I find the test code more important. The code is an executable specification. It expresses the desired truth about a system.
Test code is code that has the same lifetime as the production code. It pays to structure it as well as the production code. If a test is well-written, you should be able to understand it without reading its name.
That's an ideal, and in reality we are fallible. Thus, providing a helpful name gives the reader a second chance to understand a test. The name shouldn't, however, be your first priority.
Asynchronous monads
Asynchronous computations form monads. An article for object-oriented programmers.
This article is an instalment in an article series about monads. A previous article described how asynchronous computations form functors. In this article, you'll see that asynchronous computations also form monads. You'll learn about closely related monads: .NET Tasks and F# asynchronous workflows.
Before we start, I'm going to repeat the warning from the article about asynchronous functors. .NET Tasks aren't referentially transparent, whereas F# asynchronous computations are. You could argue, then, that .NET Tasks aren't proper monads, but you mostly observe the difference when you perform impure operations. As a general observation, when impure operations are allowed, the conclusions of this overall article series are precarious. We can't radically change how the .NET languages work, so we'll have to soldier on, pretending that impure operations are delegated to other parts of our system. Under this undue assumption, we can pretend that Task<T> forms a monad. Also, while there are differences, it sometimes helps to think of Task<T> as a sort of poor man's IO monad.
Monadic bind #
A monad must define either a bind or join function. In C#, monadic bind is called SelectMany. You can define one as an extension method on the Task<T> class:
public async static Task<TResult> SelectMany<T, TResult>( this Task<T> source, Func<T, Task<TResult>> selector) { T x = await source; return await selector(x); }
With SelectMany, you can compose various tasks and flatten as you go:
Task<int> x = AsyncValue( 42); Task<int> y = AsyncValue(1337); Task<int> z = x.SelectMany(async i => i + await y);
If you're wondering how this is useful, since C# already has async and await keywords for that purpose, I can understand you. Had you not had that language feature, monadic bind would have been helpful, but now it feels a little odd. (I haven't been deep into the bowels of how that language feature works, but from what little I've seen, monads play a central role - just as they do in the LINQ language feature.)
In F# you can define a bind function that works on Async<'a> values:
// ('a -> Async<'b>) -> Async<'a> -> Async<'b> let bind f x = async { let! x' = x return! f x' }
For both the C# and the F# examples, the exercise seems a little redundant, since they're both based on language features. The C# SelectMany implementation uses the async and await keywords, and the F# bind function uses the built-in async computation expression. For that reason, I'll also skip the section on syntactic sugar that I've included in the previous articles in this article series. Syntactic sugar is already built into the languages.
Flatten #
In the introduction you learned that if you have a Flatten or Join function, you can implement SelectMany, and the other way around. Since we've already defined SelectMany for Task<T>, we can use that to implement Flatten. In this article I use the name Flatten rather than Join. This is an arbitrary choice that doesn't impact behaviour. Perhaps you find it confusing that I'm inconsistent, but I do it in order to demonstrate that the behaviour is the same even if the name is different.
The concept of a monad is universal, but the names used to describe its components differ from language to language. What C# calls SelectMany, Scala calls flatMap, and what Haskell calls join, other languages may call Flatten.
You can always implement Flatten by using SelectMany with the identity function.
public static Task<T> Flatten<T>(this Task<Task<T>> source) { return source.SelectMany(x => x); }
The F# version uses the same implementation - it's just a bit terser:
// Async<Async<'a>> -> Async<'a> let flatten x = bind id x
In F#, id is a built-in function.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. Conceptually, I call this function return (because that's the name that Haskell uses). You don't, however, have to define a static method called Return. What's of importance is that the capability exists. For Task<T> this function already exists: It's called FromResult.
In F#, it's not built-in, but easy to implement:
// 'a -> Async<'a> let fromValue x = async { return x }
I called it fromValue inspired by the C# method name (and also because return is a reserved keyword in F#).
Left identity #
We need to identify the return function in order to examine the monad laws. Now that this is done, let's see what the laws look like for the asynchronous monads, starting with the left identity law.
[Property(QuietOnSuccess = true)] public void TaskHasLeftIdentity(Func<int, string> h_, int a) { Func<int, Task<int>> @return = Task.FromResult; Task<string> h(int x) => Task.FromResult(h_(x)); Assert.Equal(@return(a).SelectMany(h).Result, h(a).Result); }
Like in the previous article the test uses FsCheck 2.11.0 and xUnit.net 2.4.0. FScheck can generate arbitrary functions in addition to arbitrary values, but it unfortunately, it can't generate asynchronous computations. Instead, I've asked FsCheck to generate a function that I then convert to an asynchronous computation.
The code I'm using for this article is quite old, and neither FsCheck 2.11.0 nor xUnit.net 2.4.0 can handle asynchronous unit tests (a capability that later versions do have). Thus, the assertion has to force the computations to run by accessing the Result property. Not modern best practice, but it gets the point across, I hope.
In F# I wrote monad law examples using Kleisli composition. I first defined a function called fish:
// ('a -> Async<'b>) -> ('b -> Async<'c>) -> 'a -> Async<'c> let fish f g x = async { let! x' = f x return! g x' }
Keep in mind that fish is also a verb, so that's okay for a function name. The function then implements the fish operator:
let (>=>) = Async.fish
This enables us to give an example of the left identity law using Kleisli composition:
[<Property(QuietOnSuccess = true)>] let ``Async fish has left identity`` (h' : int -> string) a = let h x = async { return h' x } let left = Async.fromValue >=> h let right = h Async.RunSynchronously (left a) =! Async.RunSynchronously (right a)
The =! operator is an Unquote operator that I usually read as must equal. It's a test assertion that'll throw an exception if the left and right sides aren't equal.
Right identity #
In a similar manner, we can showcase the right identity law as a test - first in C#:
[Property(QuietOnSuccess = true)] public void TaskHasRightIdentity(int a) { Func<int, Task<int>> @return = Task.FromResult; Task<int> m = Task.FromResult(a); Assert.Equal(m.SelectMany(@return).Result, m.Result); }
Here's a Kleisli-composition-based F# property that demonstrates the right identity law for asynchronous workflows:
[<Property(QuietOnSuccess = true)>] let ``Async fish has right identity`` (f' : int -> string) a = let f x = async { return f' x } let left = f let right = f >=> Async.fromValue Async.RunSynchronously (left a) =! Async.RunSynchronously (right a)
As always, even a property-based test constitutes no proof that the law holds. I show it only to illustrate what the laws look like in 'real' code.
Associativity #
The last monad law is the associativity law that describes how (at least) three functions compose.
[Property(QuietOnSuccess = true)] public void TaskIsAssociative( Func<DateTime, int> f_, Func<int, string> g_, Func<string, byte> h_, DateTime a) { Task<int> f(DateTime x) => Task.FromResult(f_(x)); Task<string> g(int x) => Task.FromResult(g_(x)); Task<byte> h(string x) => Task.FromResult(h_(x)); Task<int> m = f(a); Assert.Equal(m.SelectMany(g).SelectMany(h).Result, m.SelectMany(x => g(x).SelectMany(h)).Result); }
This property once more relies on FsCheck's ability to generate arbitrary pure functions, which it then converts to asynchronous computations. The same does the Kleisli-composition-based F# property:
[<Property(QuietOnSuccess = true)>] let ``Async fish is associative`` (f' : int -> string) (g' : string -> byte) (h' : byte -> bool) a = let f x = async { return f' x } let g x = async { return g' x } let h x = async { return h' x } let left = (f >=> g) >=> h let right = f >=> (g >=> h) Async.RunSynchronously (left a) =! Async.RunSynchronously (right a)
It's easier to see the associativity that the law is named after when using Kleisli composition, but as the article about the monad laws explained, the two variations are equivalent.
Conclusion #
Whether you do asynchronous programming with Task<T> or Async<'a>, asynchronous computations form monads. This enables you to piecemeal compose asynchronous workflows.
Next: The State monad.
The Lazy monad
Lazy computations form a monad. An article for object-oriented programmers.
This article is an instalment in an article series about monads. A previous article described how lazy computations form a functor. In this article, you'll see that lazy computations also form a monad.
SelectMany #
A monad must define either a bind or join function. In C#, monadic bind is called SelectMany. You can define one as an extension method on the Lazy<T> class:
public static Lazy<TResult> SelectMany<T, TResult>( this Lazy<T> source, Func<T, Lazy<TResult>> selector) { return new Lazy<TResult>(() => selector(source.Value).Value); }
While the implementation seemingly forces evaluation by accessing the Value property, this all happens inside a lambda expression that defers execution.
If x is a Lazy<int> and SlowToString is a function that takes an int as input and returns a Lazy<string> you can compose them like this:
Lazy<string> y = x.SelectMany(SlowToString);
The result is another lazy computation that, when forced, will produce a string.
Query syntax #
Monads also enable query syntax in C# (just like they enable other kinds of syntactic sugar in languages like F# and Haskell). As outlined in the monad introduction, however, you must add a special SelectMany overload:
public static Lazy<TResult> SelectMany<T, U, TResult>( this Lazy<T> source, Func<T, Lazy<U>> k, Func<T, U, TResult> s) { return source.SelectMany(x => k(x).Select(y => s(x, y))); }
This would enable you to rewrite the above example like this:
Lazy<string> y = from i in x from s in SlowToString(i) select s;
The behaviour is the same as above. It's just two different ways of writing the same expression. The C# compiler desugars the query-syntax expression to one that composes with SelectMany.
Flatten #
In the introduction you learned that if you have a Flatten or Join function, you can implement SelectMany, and the other way around. Since we've already defined SelectMany for Lazy<T>, we can use that to implement Flatten. In this article I use the name Flatten rather than Join. This is an arbitrary choice that doesn't impact behaviour. Perhaps you find it confusing that I'm inconsistent, but I do it in order to demonstrate that the behaviour is the same even if the name is different.
The concept of a monad is universal, but the names used to describe its components differ from language to language. What C# calls SelectMany, Scala calls flatMap, and what Haskell calls join, other languages may call Flatten.
You can always implement Flatten by using SelectMany with the identity function.
public static Lazy<T> Flatten<T>(this Lazy<Lazy<T>> source) { return source.SelectMany(x => x); }
You could also compose the above x and SlowToString with Select and Flatten, like this:
Lazy<Lazy<string>> nested = x.Select(SlowToString); Lazy<string> flattened = nested.Flatten();
The flattened value remains deferred until you force execution.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. Conceptually, I call this function return (because that's the name that Haskell uses). You don't, however, have to define a static method called Return. What's of importance is that the capability exists. For Lazy<T> in C# the idiomatic way would be to use a constructor, but the version of .NET I'm using for this code (this is actually code I wrote years ago) doesn't have such a constructor (newer versions do). Instead, I'll define a function:
public static Lazy<T> Return<T>(T x) { return new Lazy<T>(() => x); }
In other words, Return wraps a pre-existing value in a lazy computation.
Left identity #
We need to identify the return function in order to examine the monad laws. Now that this is done, let's see what the laws look like for the Lazy monad, starting with the left identity law.
[Property(QuietOnSuccess = true)] public void LazyHasLeftIdentity(Func<int, string> h_, int a) { Func<int, Lazy<int>> @return = Lazy.Return; Lazy<string> h(int x) => Lazy.Return(h_(x)); Assert.Equal(@return(a).SelectMany(h).Value, h(a).Value); }
Like in the previous article the test uses FsCheck 2.11.0 and xUnit.net 2.4.0. FScheck can generate arbitrary functions in addition to arbitrary values, but it unfortunately, it can't generate lazy computations. Instead, I've asked FsCheck to generate a function that I then convert to a lazy computation.
In order to compare the values, the assertion has to force evaluation by reading the Value properties.
Right identity #
In a similar manner, we can showcase the right identity law as a test.
[Property(QuietOnSuccess = true)] public void LazyHasRightIdentity(Func<string, int> f_, string a) { Func<string, Lazy<int>> f = x => Lazy.Return(f_(x)); Func<int, Lazy<int>> @return = Lazy.Return; Lazy<int> m = f(a); Assert.Equal(m.SelectMany(@return).Value, m.Value); }
As always, even a property-based test constitutes no proof that the law holds. I show it only to illustrate what the laws look like in 'real' code.
Associativity #
The last monad law is the associativity law that describes how (at least) three functions compose.
[Property(QuietOnSuccess = true)] public void LazyIsAssociative( Func<int, string> f_, Func<string, byte> g_, Func<byte, TimeSpan> h_, int a) { Lazy<string> f(int x) => Lazy.Return(f_(x)); Lazy<byte> g(string x) => Lazy.Return(g_(x)); Lazy<TimeSpan> h(byte x) => Lazy.Return(h_(x)); Lazy<string> m = f(a); Assert.Equal(m.SelectMany(g).SelectMany(h).Value, m.SelectMany(x => g(x).SelectMany(h)).Value); }
This property once more relies on FsCheck's ability to generate arbitrary pure functions, which it then converts to lazy computations.
Conclusion #
The Lazy functor (which is also an applicative functor) is also a monad. This can be used to combine multiple lazily computed values into a single lazily computed value.
Next: Asynchronous monads.
Waiting to never happen
An example of how non-deterministic code can cause test cases to wither.
It seems to me that when people discuss functional programming, they spend much time discussing side effects and how to avoid them. Sometimes, they almost forget that non-deterministic behaviour is also something to avoid.
On the other hand, we've known for a long time that we should eradicate non-determinism in tests. Martin Fowler's article, however, mostly discusses false positives: Tests that fail even when no defect is manifest.
Unit tests may also exhibit false negatives. This can happen for a variety of reason. In my article Tautological assertion I describe one example.
The passing of time, however, has a tendency to introduce decay. This may apply to test suites as well. If a test or the System Under Test depends on the current time, a test may over time transition from a proper test to one that still passes, but for the wrong reason.
A test example #
I was recently looking at this test:
[Fact] public async Task ChangeDateToSoldOutDate() { var r1 = Some.Reservation; var r2 = Some.Reservation .WithId(Guid.NewGuid()) .TheDayAfter() .WithQuantity(10); var db = new FakeDatabase(); db.Grandfather.Add(r1); db.Grandfather.Add(r2); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var dto = r1.WithDate(r2.At).ToDto(); var actual = await sut.Put(r1.Id.ToString("N"), dto); var oRes = Assert.IsAssignableFrom<ObjectResult>(actual); Assert.Equal( StatusCodes.Status500InternalServerError, oRes.StatusCode); }
It's from the code base that accompanies my book Code That Fits in Your Head. It's a false negative waiting to happen. What's the problem?
Before I start describing the problem, I think that I owe you a short explanation of what you're looking at. The book has a single example code base that it uses to showcase various heuristics and techniques. The code base implements an online restaurant reservation REST API. I've previously discussed that code base on this blog.
This particular test exercises the following test case: A client can use the REST API to change an existing reservation. When it does that, the API should check that all business rules apply. Particularly, in this case, if you have an existing reservation (r1), but try to change it to another date, and that other date is already sold out, the update should be refused.
The test uses backdoor manipulation to establish the initial state. It's a state-based integration test that uses an in-memory Fake database. It adds two reservations (r1 and r2) to the database, on two different days.
What's not at all clear from the above code is that that 10 is the Grandfather.Restaurant's maximum capacity. (This is a fair criticism against this test, but not what this article is about.) It effectively means that the restaurant is sold out that day.
The test then, in the act phase, tries to change r1 to the date that's sold out and Put that change.
The assertion checks that this isn't possible.
A false negative waiting to happen #
What's the problem with the above test?
The problem is that when I wrote it, it exercised the above test case, but now it no longer does.
At this point, you're probably wondering. The test case is supposed to change the date of r1 to the date of r2, but no dates are visible in the test. Which dates does the test use?
The answer may be found in the Some class:
public readonly static Reservation Reservation = new Reservation( new Guid(0x81416928, 0xC236, 0x4EBF, 0xA4, 0x50, 0x24, 0x95, 0xA4, 0xDA, 0x92, 0x30), Now, new Email("x@example.net"), new Name(""), 1);
Some.Reservation is an immutable test datum. It's intended to be used as a representative example of a Reservation value. The reservation date and time (the At property) is another immutable test datum:
public readonly static DateTime Now = new DateTime(2022, 4, 1, 20, 15, 0);
I wrote most of that code base in 2020. April 1st 2022 seemed far in the future, and I needed a value that could represent 'approximately' the current time. It didn't have to be the day the code would run, but (as it turns out) it's important that this date isn't in the past. Which it now is.
What happens now that Some.Reservation is in the past?
Nothing, and that's exactly what is the problem.
A new path #
Once the clock rolled over from 2022-04-02 20:14:59 to 2022-04-02 20:15:00, the pathway through the code changed. Why April 2 and not April 1? Because the date of importance in the test is TheDayAfter, and TheDayAfter is defined like this:
public static Reservation TheDayAfter(this Reservation reservation) { return reservation.AddDate(TimeSpan.FromDays(1)); }
So r2.At is 20:15 April 2, 2022.
Before 2022-04-02 20:15:00 the test would exercise the test case it was supposed to. After all, I did write the test before I wrote the implementation, and I did see it fail before I saw it pass.
Once, however, dto is in the past, another pathway takes over. The Maître d's core decision logic (WillAccept) contains this Guard Clause:
if (candidate.At < now) return false;
Long before the domain model investigates whether it can accommodate a reservation, it rejects all reservations in the past. The calling code, however, only sees that the return value is false. In other words, the externally observable behaviour is the same. This also means that test's assertion still passes. From the outside, you can't tell the difference.
Coverage decay #
If the behaviour is stable, then why is this a problem?
This is a problem because this decreases test coverage. While code coverage is a useless target measure, it's not a completely useless metric. The absolute percentage is less relevant than the trend. If code coverage decreases, one should at least investigate.
Here, specifically, it means that I thought I had a particular test case covered, and in reality it turns out that that's no longer the case. Now the test just verifies that you can't update past reservations, regardless of application state. Other tests already verify that, however, so this test now became redundant.
As I've described before, each test case exercises a particular path through the System Under Test:
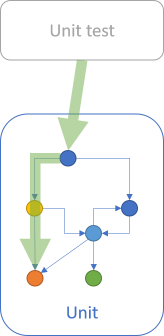
If you have high code coverage, an aggregate diagram might look like this:
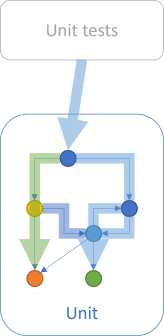
Notice that the top box now says Unit tests in plural. Together, the tests exercise most pathways through the code. There's one pathway not exercised: The path from the light blue node to the orange node. The point is that this diagram illustrates high code coverage, not complete code coverage. The following argument applies to that general situation.
What happened with the above test is that coverage decayed.
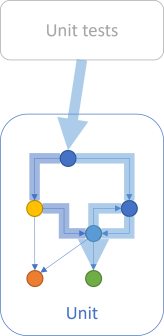
In this figure, the green pathway is no longer exercised.
Not only did coverage decrease: Unless you're monitoring code coverage, you probably didn't notice. The code didn't change. Time just passed.
Threat to refactoring #
Why is this a problem? After all, code coverage isn't a goal; it's just a measure.
As Martin Fowler writes:
"to refactor, the essential precondition is [...] solid tests"
A good test suite verifies that the behaviour of your software doesn't change as you reorganise the code. The underlying assumption is that the test suite exercises important use cases and protects against regressions.
The above test is an example of a test case that silently disappears. If you think that your tests cover all important use cases, you may feel confident refactoring. After all, if all tests pass, you didn't break any existing behaviour.
Unbeknownst to you, however, the test suite may become less trustworthy. As time passes, test cases may disappear, as exemplified by the above test. While the test suite may be passing, a refactoring could introduce a regression - of behaviour you believed to be already covered.
Under the radar #
Why didn't I catch this earlier? After all, I'd already identified the problem in the code base. Once I realised the problem, I took steps to remedy it. I loaded the code base on a spare computer and changed the machine's year to a future year (2038, if I recall correctly). Then I ran the tests to see which ones failed.
I examined each failing test to verify that it actually failed because of the time and date. Then I corrected the test to make it relative to the system clock.
That took care of all the tests that would eventually break. On the other hand, it didn't unearth any of the tests that over time silently would become false negatives.
Make it relative #
Fixing the above test was easy:
[Fact] public async Task ChangeDateToSoldOutDate() { var r1 = Some.Reservation.WithDate(DateTime.Now.AddDays(8).At(20, 15)); var r2 = r1 .WithId(Guid.NewGuid()) .TheDayAfter() .WithQuantity(10); var db = new FakeDatabase(); db.Grandfather.Add(r1); db.Grandfather.Add(r2); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var dto = r1.WithDate(r2.At).ToDto(); var actual = await sut.Put(r1.Id.ToString("N"), dto); var oRes = Assert.IsAssignableFrom<ObjectResult>(actual); Assert.Equal( StatusCodes.Status500InternalServerError, oRes.StatusCode); }
The only change is to the creation of r1 and r2. The test now explicitly sets the r1 date eight days in the future. It also derives r2 from r1, which makes the relationship between the two values more explicit. This in itself is a small improvement, I think.
Deterministic behaviour #
More than one person has told me that I obsess over details to a degree that can't be expected of most developers. If that's true, problems like this are likely to go unnoticed. After all, I discovered the problem because I was carefully reviewing each test more than a year after I originally wrote it. While I had a reason to do that, we can't expect developers to do that.
Are we doomed to suffer this kind of error, then? I don't have a silver bullet for you, but I don't think that all is lost. A little discipline may help. As I write in Code That Fits in Your Head, pair programming or code reviews can help raise awareness of issues.
On the tactical level, you might want to consider a policy that discourages absolute dates and times in unit tests.
On the strategic level, you may want to adopt the Functional Core, Imperative Shell architecture. After all, pure functions are intrinsically testable.
As I wrote in the beginning of this article, most people tend to focus on how to avoid side effects when discussing functional programming. A pure function, however, must be both side-effect-free and deterministic.
This means that instead of learning many specific rules (such as not using absolute time in unit tests), you may focus on one general rule: Write and test pure functions.
To be honest, though, this rule doesn't solve all problems. Even in a functional-core-imperative-shell architecture, the imperative shell isn't pure. The above integration test is, unfortunately, a test of the imperative shell. It's already using the SystemClock, and that's no oversight on my part. While I do favour the test pyramid, I also write integration tests - just as the test pyramid encourages me to do. I find it valuable that integration tests integrate as many components as possible. The more real components an integration test uses, the better the chance that it uncovers problems.
With integration tests, then, diligence is required to keep tests deterministic. In that context you can't rely on a universal rule like just write pure functions, because at the boundaries, programs aren't functional. Instead, some diligence and discipline is required. At least, I don't see other alternatives, but perhaps you do?
Conclusion #
If you use absolute dates in unit tests, what was once a future date may some day become a past date. This can change which pathways of the System Under Test an automated test exercises.
Is this important? It's probably not the most pressing problem you may run into. Even if test coverage silently decays, it may not be a problem if you never refactor the code in question. It's only if, during a refactoring, you introduce a defect that goes unnoticed that this may become a problem. It doesn't seem like the most likely of errors, but on the other hand, these kinds of unexpected problems have a tendency to occur at the most inopportune moments.
Comments
Why have you decided to make the date of the reservation relative to the SystemClock, and not the other way around? Would it be more deterministic to use a faked system clock instead?
Laszlo, thank you for asking. I wrote a new article to answer your question.
The Identity monad
Probably one of the least useful monads. An article for object-oriented developers.
This article is an instalment in an article series about monads.
The Identity functor is another example of a functor that also forms a monad. Contrary to useful monads like list, Maybe, and Either, the Identity monad isn't particularly useful. In Haskell it serves a few niche positions, for example when it comes to monad transformers. It's possible to define abstractions at a higher level in Haskell than it is in many other languages. Some of those abstractions involve monads. The Identity monad can plug into these abstractions as a 'do-nothing' monad, a bit like the Null Object pattern can supply a 'do-nothing' implementation of an interface.
Other languages with which I'm proficient (C#, F#) don't enable that kind of abstraction, and I've never felt the need to actually use the Identity monad in those languages. Still, the Identity monad exists mathematically and conceptually, and it can be useful to know of that existence. This implies, like the Null Object pattern, that some abstractions can be simplified by 'plugging in' the Identity monad. The alternative would have had to involve some hand-waving about special cases.
The code in this article continues the implementation shown in the article about the Identity functor.
SelectMany #
A monad must define either a bind or join function. In C#, monadic bind is called SelectMany. For Identity<T> the implementation is trivial:
public Identity<TResult> SelectMany<TResult>(Func<T, Identity<TResult>> selector) { return selector(Item); }
This is an instance method on Identity<T>, which means that the Item property has the type T. Since the selector return a new Identity<TResult>, the method can simply return that value.
Query syntax #
As usual, you can implement C# query syntax with a boilerplate overload of SelectMany:
public Identity<TResult> SelectMany<U, TResult>( Func<T, Identity<U>> k, Func<T, U, TResult> s) { return SelectMany(x => k(x).Select(y => s(x, y))); }
The implementation is the same as in the previous articles in this article series. If it looks a little different than, say, the implementation for the Maybe monad, it's only because this SelectMany overload is an instance method, whereas the Maybe implementation is an extension method.
Query syntax enables syntactic sugar like this:
Identity<int> i = from x in new Identity<int>(39) from y in new Identity<string>("foo") select x + y.Length;
The C# compiler infers that x is an int and y is a string.
Flatten #
As the monad introduction also points out, if you have monadic bind (SelectMany) you can always implement a function to flatten a nested functor. This function is sometimes called join and sometimes (perhaps more intuitively) flatten. Here I've chosen to call it Flatten:
public static Identity<T> Flatten<T>(this Identity<Identity<T>> source) { return source.SelectMany(x => x); }
Even though the other methods shown so far have been instance methods, Flatten has to be an extension method, since the source is a nested Identity<Identity<T>>. There's no class of that specific type - only Identity<T>.
If there's one useful aspect of the Identity monad, it may be that it reveals the concept of a nested functor in all its triviality:
Identity<Identity<string>> nested = new Identity<Identity<string>>(new Identity<string>("bar")); Identity<string> flattened = nested.Flatten();
Recall: A monad is a functor you can flatten.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. Conceptually, I call this function return (because that's the name that Haskell uses). You don't, however, have to define a static method called Return. What's of importance is that the capability exists. For Identity<T> in C# the idiomatic way would be to use a constructor. This constructor does double duty as monadic return:
public Identity(T item) { Item = item; }
In other words, return just wraps a value in the Identity<T> container.
Left identity #
We need to identify the return function in order to examine the monad laws. Let's see what they look like for the Identity monad, starting with the left identity law.
[Property(QuietOnSuccess = true)] public void IdentityHasLeftIdentity(Func<int, Identity<string>> h, int a) { Func<int, Identity<int>> @return = i => new Identity<int>(i); Assert.Equal(@return(a).SelectMany(h), h(a)); }
This example is a bit different compared to the previous examples, since it uses FsCheck 2.11.0 and xUnit.net 2.4.0. FScheck can generate arbitrary functions in addition to arbitrary values, so I've simply asked it to generate some arbitrary h functions.
Right identity #
In a similar manner, we can showcase the right identity law as a test.
[Property(QuietOnSuccess = true)] public void IdentityHasRightIdentity(Func<string, Identity<int>> f, string a) { Func<int, Identity<int>> @return = i => new Identity<int>(i); Identity<int> m = f(a); Assert.Equal(m.SelectMany(@return), m); }
As always, even a property-based test constitutes no proof that the law holds. I show it only to illustrate what the laws look like in 'real' code.
Associativity #
The last monad law is the associativity law that describes how (at least) three functions compose.
[Property(QuietOnSuccess = true)] public void IdentityIsAssociative( Func<int, Identity<string>> f, Func<string, Identity<byte>> g, Func<byte, Identity<TimeSpan>> h, int a) { Identity<string> m = f(a); Assert.Equal(m.SelectMany(g).SelectMany(h), m.SelectMany(x => g(x).SelectMany(h))); }
This property once more relies on FsCheck's ability to generate arbitrary pure functions.
F# #
While the Identity monad is built into the Haskell standard library, there's no Identity monad in F#. While it can be occasionally useful in Haskell, Identity is as useless in F# as it is in C#. Again, that doesn't imply that you can't define it. You can:
type Identity<'a> = Identity of 'a module Identity = // Identity<'a> -> 'a let get (Identity x) = x // ('a -> 'b) -> Identity<'a> -> Identity<'b> let map f (Identity x) = Identity (f x) // ('a -> Identity<'b>) -> Identity<'a> -> Identity<'b> let bind f (Identity x) : Identity<_> = f x
Here I've repeated the functor implementation from the article about the Identity functor, but now also included the bind function.
You can use such a module to support syntactic sugar in the form of computation expressions:
type IdentityBuilder() = member _.Bind(x, f) = Identity.bind f x member _.Return x = Identity x member _.ReturnFrom x = x let identity = IdentityBuilder ()
This enables you to write code like this:
let i = identity { let! x = Identity "corge" let! y = Identity 47 return y - x.Length }
Here, i is a value of the type Identity<int>.
Conclusion #
If the Identity monad is useful in languages like C# and F#, I have yet to encounter a use case. Even so, it exists. It is also, perhaps, the most naked illustration of what a functor and monad is. As such, I think it may be helpful to study.
Next: The Lazy monad.
An Either monad
The Either sum type forms a monad. An article for object-oriented programmers.
This article is an instalment in an article series about monads.
The Either sum type is a useful data type that forms a functor. Actually, it forms two functors. Like many other useful functors, it also forms a monad. Again, more than one monad is possible. In this article I'll focus on the 'usual' monad instance where mapping takes place over the right side. If you swap left and right, however, you can also define a monad that maps over the left side. Try it; it's a good exercise.
Either is also known as Result, in which case right is usually called success or OK, while left is called error or failure.
In this article, I'll base the C# implementation on the code from Church-encoded Either.
Join #
A monad must define either a bind or join function. As outlined in the introduction to monads, if you have one, you can use it to implement the other. For variety's sake, in this article series I do both. I also vary the names when there's no clear idiomatic naming convention. For this version of Either, I've chosen to start with a method called Join:
public static IEither<L, R> Join<L, R>(this IEither<L, IEither<L, R>> source) { return source.Match( onLeft: l => new Left<L, R>(l), onRight: r => r); }
This method flattens a nested Either value. If the outer Either is a left case, the method returns a new Left<L, R>(l) value, which fits the required return type. If the outer Either is a right case, it contains another, nested Either value that it can return.
As already described in the article Church-encoded Either, you can use Either values instead of exceptions. While that article already gives an example, the Either in that value isn't nested. This, however, can easily happen when you try to compose calculations that may fail. Another example may involve parsing. Here are two simple parsers:
public static IEither<string, DateTime> TryParseDate(string candidate) { if (DateTime.TryParse(candidate, out var d)) return new Right<string, DateTime>(d); else return new Left<string, DateTime>(candidate); } public static IEither<string, TimeSpan> TryParseDuration(string candidate) { if (TimeSpan.TryParse(candidate, out var ts)) return new Right<string, TimeSpan>(ts); else return new Left<string, TimeSpan>(candidate); }
These functions try to parse candidate values to more structured data types. If parsing fails, they return the candidate value so that calling code may get a chance to inspect and report the string that caused a failure. What happens if you try to compose these two functions?
IEither<string, DateTime> dt = TryParseDate("2022-03-21"); IEither<string, TimeSpan> ts = TryParseDuration("2"); IEither<string, IEither<string, DateTime>> nested = dt.Select(d => ts.Select(dur => d + dur));
Composing the results of these two functions produces a nested result that you can flatten with Join:
IEither<string, DateTime> flattened = nested.Join();
Using Join for that purpose is, however, often awkward, so a better option is to flatten as you go.
SelectMany #
Monadic bind (in C# called SelectMany) enables you to flatten as you go. As also shown in the monad introduction, if you already have Join you can always implement SelectMany like this:
public static IEither<L, R1> SelectMany<L, R, R1>( this IEither<L, R> source, Func<R, IEither<L, R1>> selector) { return source.Select(selector).Join(); }
The SelectMany method makes the above composition a little easier:
IEither<string, DateTime> result = dt.SelectMany(d => ts.Select(dur => d + dur));
Instead of having to flatten a nested result, you can flatten as you go. I think that Scala's flatMap is a better name for that operation than SelectMany, but the behaviour is the same. If you're wondering why it's called SelectMany, see my attempt at an explanation in the article about the list monad. The name makes modest sense in that context, but in the context of Either, that meaning is lost.
Query syntax #
Perhaps you still find the above composition awkward. After all, you have to nest a Select inside a SelectMany. Is there a simpler way?
One option is to use query syntax, but in order to do that, you must (again as outlined in the monad introduction) add a special boilerplate SelectMany overload:
public static IEither<L, R1> SelectMany<L, R, R1, U>( this IEither<L, R> source, Func<R, IEither<L, U>> k, Func<R, U, R1> s) { return source.SelectMany(x => k(x).Select(y => s(x, y))); }
This enables you to rewrite the above composition like this:
IEither<string, DateTime> result = from d in dt from dur in ts select d + dur;
It's often a question of subjectivity whether you like one alternative over the other, but the behaviour is the same.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. Conceptually, I call this function return (because that's the name that Haskell uses). You don't, however, have to define a static method called Return. What's of importance is that the capability exists. For Either<L, R> in C# the idiomatic way would be to use a constructor. This constructor does double duty as monadic return:
public Right(R right)
In other words, return wraps a value in a right case.
Why not the left case? Because it wouldn't type-check. A return function should take a value of the type R and return an IEither<L, R>. The Left constructor, however, doesn't take an R value - it takes an L value.
Left identity #
We need to identify the return function in order to examine the monad laws. Let's see what they look like for the Either monad, starting with the left identity law.
[Theory] [InlineData("2")] [InlineData("2.3:00")] [InlineData("4.5:30")] [InlineData("0:33:44")] [InlineData("foo")] public void LeftIdentityLaw(string a) { Func<string, IEither<string, string>> @return = s => new Right<string, string>(s); Func<string, IEither<string, TimeSpan>> h = TryParseDuration; Assert.Equal(@return(a).SelectMany(h), h(a)); }
As always, even a parametrised test constitutes no proof that the law holds. I show the tests to illustrate what the laws look like in 'real' code.
Right identity #
In a similar manner, we can showcase the right identity law as a test.
[Theory] [InlineData("2022-03-22")] [InlineData("2022-03-21T16:57")] [InlineData("bar")] public void RightIdentityLaw(string a) { Func<string, IEither<string, DateTime>> f = TryParseDate; Func<DateTime, IEither<string, DateTime>> @return = d => new Right<string, DateTime>(d); IEither<string, DateTime> m = f(a); Assert.Equal(m.SelectMany(@return), m); }
The parameters supplied as a will cause m to be both Left and Right values, but the test demonstrates that the law holds in both cases.
Associativity #
The last monad law is the associativity law that describes how (at least) three functions compose. We're going to need three functions. I'm going to reuse TryParseDuration and add two new Either-valued functions:
public static IEither<string, double> DaysForward(TimeSpan ts) { if (ts < TimeSpan.Zero) return new Left<string, double>($"Negative durations not allowed: {ts}."); return new Right<string, double>(ts.TotalDays); } public static IEither<string, int> Nat(double d) { if (d % 1 != 0) return new Left<string, int>($"Non-integers not allowed: {d}."); if (d < 1) return new Left<string, int>($"Non-positive numbers not allowed: {d}."); return new Right<string, int>((int)d); }
These silly functions are only here for purposes of demonstration. Don't try to infer any deep meaning from them.
Designating them f, g, and h, we can use them to express the monad associativity law:
[Theory] [InlineData("2")] [InlineData("-2.3:00")] [InlineData("4.5:30")] [InlineData("0:33:44")] [InlineData("0")] [InlineData("foo")] public void AssociativityLaw(string a) { Func<string, IEither<string, TimeSpan>> f = TryParseDuration; Func<TimeSpan, IEither<string, double>> g = DaysForward; Func<double, IEither<string, int>> h = Nat; var m = f(a); Assert.Equal(m.SelectMany(g).SelectMany(h), m.SelectMany(x => g(x).SelectMany(h))); }
The test cases supplied via the [InlineData] attributes comprise a set of values that make their way through the composition to varying degrees. "2" makes it all the way through to a Right value, because it encodes a two-day duration. It's both a positive value, greater than zero, and an integer. The other test cases become Left values at various stages in the composition, being either a non-number, fractional, zero, or negative.
Conclusion #
Either (AKA Result) is another useful data structure that forms a monad. You can use it instead of throwing exceptions. Its monadic nature enables you to compose multiple Either-valued functions in a sane and elegant way.
Next: The Identity monad.
At the boundaries, applications aren't functional
Ten years later.
In 2011 I published an article titled At the Boundaries, Applications are Not Object-Oriented. It made the observation that at the edges of systems, where software interacts with either humans or other software, interactions aren't object-oriented. The data exchanged is exactly that: data.
A common catchphrase about object-oriented design is that objects are data with behaviour. In a user interface, a REST API, at the command line, etcetera, data is transmitted, but behaviour is not.
The article was one of those unfortunately unsatisfying articles that point out a problem without offering a solution. While I don't like to leave readers hanging like that, I on the other hand think that it's important sometimes to ask open-ended questions. Here's a problem. Can anyone offer a solution?
People occasionally come by that old article and ask me if I've changed my mind since then. The short answer is that I believe that the problem persists. I may, however, today have another approach to it.
Functional programming #
Starting around the time of the original article, I became interested in functional programming (FP). The more I've learned about it, the better it seems to address my concerns of eleven years ago.
I don't know if FP is a silver bullet (although I'd like to think so), but at least I find that I have fewer impedance mismatch issues than I did with object-oriented programming (OOP). In FP, after all, data is just data.
Except when it isn't, but more about that later.
It's easier to reconcile the FP notion of data with what actually goes on at the boundaries of a system.
Perhaps I should clarify what I mean by the word boundary. This is where a software system interacts with the rest of the world. This is where it receives HTTP requests and answers with HTTP responses. This is where it queries its database. This is where it sends emails. This is where it reads files from disk. This is where it repaints user interfaces. In short, the outermost circle in ports and adapters architecture.
Notice that what crosses the boundary tends to be data. JSON or XML documents, tabular data streams, flat files, etcetera. In OOP, your training tells you that you should associate some behaviour with data, and that's what creates dissonance. We introduce Data Transfer Objects (DTO) even though a DTO
"is one of those objects our mothers told us never to write."
We almost have to do violence to ourselves to introduce a DTO in an object-oriented code base, yet grudgingly we accept that this is probably better than the alternative.
In FP, on the other hand, that's just natural.
To paraphrase the simple example from the old article, imagine that you receive data like this as input:
{
"firstName": "Mark",
"lastName": "Seemann"
}
If we wanted to capture that structure as a type, in F# you'd write a type like this:
type Name = { FirstName : string; LastName : string }
And while you might feel icky defining such a DTO-like type in OOP, it's perfectly natural and expected in FP.
That type even supports JSON serialization and deserialization without further ceremony:
let opts = JsonSerializerOptions (PropertyNamingPolicy = JsonNamingPolicy.CamelCase) let n = JsonSerializer.Deserialize<Name> (json, opts)
where json might contain the above JSON fragment.
To summarise so far: Data crosses the boundaries of systems - not objects. Since FP tends to separate data from behaviour, that paradigm feels more natural in that context.
Not all peaches and cream #
FP is, however, not a perfect fit either. Let's paraphrase the above medial summary: Data crosses the boundaries of systems - not functions.
FP is more than just functions and data. It's also about functions as first-class concepts, including functions as values, and higher-order functions. While an object is data with behaviour, closures are behaviour with data. Such first-class values cross system boundaries with the same ease as objects do: Not very well.
I was recently helping a client defining a domain-specific language (DSL). I wrote a proof of concept in Haskell based on Abstract Syntax Trees (AST). Each AST would typically be defined with copious use of lambda expressions. There was also an existential type involved.
At one time, the question of persistence came up. At first I thought that you could easily serialize those ASTs, since, after all, they're just immutable values. Then I realised that while that's true, most of the constituent values were functions. There's no clear way to serialize a function, other than in code.
Functions don't easily cross boundaries, for the same reasons that objects don't.
So while FP seems like a better fit when it comes to modelling data, at the boundaries, applications aren't functional.
Weak or strong typing? #
In my original article, I attempted to look ahead. One option I considered was dynamic typing. Instead of defining a DTO that mirrors a particular shape of data (e.g. a JSON document), would it be easier to parse or create a document on the fly, without a static type?
I occasionally find myself doing that, as you can see in my article To ID or not to ID. The code base already used Json.NET, and I found it easier to use the JToken API to parse documents, rather than having to maintain a static type whose only raison d'être was to mirror a JSON document. I repeat an example here for your convenience:
// JToken -> UserData<string> let private parseUser (jobj : JToken) = let uid = jobj.["id"] |> string let fn = jobj.["firstName"] |> Option.ofObj |> Option.map string let ln = jobj.["lastName"] |> Option.ofObj |> Option.map string let email = jobj.["primaryEmail"] |> Option.ofObj |> Option.map (string >> MailAddress) { Id = uid FirstName = fn LastName = ln Email = email Identities = [] Permissions = [] }
Likewise, I also used JObject to create and serialize new JSON documents. The To ID or not to ID article also contains an example of that.
F# types are typically one-liners, like that above Name example. If that's true, why do I shy away from defining a static type that mirrors the desired JSON document structure?
Because typing (the other kind of typing) isn't a programming bottleneck. The cost of another type isn't the time it takes to write the code. It's the maintenance burden it adds.
One problem you'll commonly have when you define DTOs as static types is that the code base will contain more than one type that represents the same concept. If these types are too similar, it becomes difficult for programmers to distinguish between them. As a result, functionality may inadvertently be coupled to the wrong type.
Still, there can be good reasons to introduce a DTO type and a domain model. As Alexis King writes,
"Consider: what is a parser? Really, a parser is just a function that consumes less-structured input and produces more-structured output."
This is the approach I took in Code That Fits in Your Head. A ReservationDto class has almost no invariants. It's just a bag of mutable and nullable properties; it's less-structured data.
The corresponding domain model Reservation is more-structured. It's an immutable Value Object that guarantees various invariants: All required data is present, quantity is a natural number, you can't mutate the object, and it has structural equality.
In that case, ReservationDto and Reservation are sufficiently different. I consider their separate roles in the code base clear and distinct.
Conclusion #
In 2011 I observed that at the boundaries, applications aren't object-oriented. For years, I've thought it a natural corollary that likewise, at the boundaries, applications aren't functional, either. On the other hand, I don't think I've explicitly made that statement before.
A decade after 2011, I still find object-oriented programming incongruent with how software must work in reality. Functional programming offers an alternative that, while also not perfectly aligned with all data, seems better aligned with the needs of working software.
The Maybe monad
The Maybe sum type forms a monad. An article for object-oriented programmers.
This article is an instalment in an article series about monads.
The Maybe sum type is a useful data type that forms a functor. Like many other useful functors, it also forms a monad.
It can be useful when querying another data structure (like a list or a tree) for a value that may or may not be present. It's also useful when performing a calculation that may not be possible, such as taking the square root of of a number, or calculating the average of a collection of values. A third common use case is when parsing a value, although usually, the Either sum type is often a better option for that task.
Bind #
A monad must define either a bind or join function. In C#, monadic bind is called SelectMany. Depending on how you've implemented Maybe<T> the details of the implementation may vary, but the observable behaviour must always be the same. In this article I'm going to continue to use the Maybe<T> class first shown in the article about the Maybe functor. (That's not really my favourite implementation, but it doesn't matter.)
In that code base, I chose to implement SelectMany as an extension method. Why I didn't use an instance method I no longer remember. Again, this doesn't matter.
public static Maybe<TResult> SelectMany<T, TResult>( this Maybe<T> source, Func<T, Maybe<TResult>> selector) { if (source.HasItem) return selector(source.Item); else return new Maybe<TResult>(); }
If the source has an item, SelectMany calls selector with the value and returns the result. If not, the result is an empty Maybe<TResult>.
Monadic bind becomes useful when you have more than one function that returns a monadic value. Consider, for example, this variation of Average:
public static Maybe<double> Average(IEnumerable<double> values) { if (values.Any()) return new Maybe<double>(values.Average()); else return new Maybe<double>(); }
You can't calculate the average of an empty collection, so if values is empty, this function returns an empty Maybe<double>.
If you only needed this Average function, then you could use Maybe's functor affordance to map the result. On the other hand, imagine that you'd like to pass the Average result to this Sqrt function:
public static Maybe<double> Sqrt(double d) { var result = Math.Sqrt(d); switch (result) { case double.NaN: case double.PositiveInfinity: return new Maybe<double>(); default: return new Maybe<double>(result); } }
This is another calculation that may not be possible. If you try to compose Average and Sqrt with Select (the functor's map function), you'd get a Maybe<Maybe<double>>. Fortunately, however, monads are functors you can flatten:
[Theory] [InlineData(new double[0], -100)] [InlineData(new double[] { 5, 3 }, 2)] [InlineData(new double[] { 1, -2 }, -100)] public void ComposeAverageAndSqrt(double[] values, double expected) { Maybe<double> actual = Average(values).SelectMany(Sqrt); Assert.Equal(expected, actual.GetValueOrFallback(-100)); }
The SelectMany method flattens as it goes. Viewed in this way, Scala's flatMap seems like a more appropriate name.
The above test demonstrates how SelectMany returns a flattened Maybe<double>. The first test case has zero elements, so the Average method is going to return an empty Maybe<double>. SelectMany handles that gracefully by returning another empty value.
In the second test case Average returns a populated value that contains the number 4. SelectMany passes 4 to Sqrt, which returns 2 wrapped in a Maybe<double>.
In the third test case, the average is -.5, wrapped in a Maybe<double>. SelectMany passes -.5 on to Sqrt, which returns an empty value.
Query syntax #
Monads also enable query syntax in C# (just like they enable other kinds of syntactic sugar in languages like F# and Haskell). As outlined in the monad introduction, however, you must add a special SelectMany overload:
public static Maybe<TResult> SelectMany<T, U, TResult>( this Maybe<T> source, Func<T, Maybe<U>> k, Func<T, U, TResult> s) { return source.SelectMany(x => k(x).Select(y => s(x, y))); }
As I also mentioned in the monad introduction, it seems to me that you can always implement this overload with the above expression. Once this overload is in place, you can rewrite the above composition in query syntax, if that's more to your liking:
[Theory] [InlineData(new double[0], -100)] [InlineData(new double[] { 5, 3 }, 2)] [InlineData(new double[] { 1, -2 }, -100)] public void ComposeAverageAndSqrtWithQuerySyntax(double[] values, double expected) { Maybe<double> actual = from a in Average(values) from s in Sqrt(a) select s; Assert.Equal(expected, actual.GetValueOrFallback(-100)); }
In this case, query syntax is more verbose, but the behaviour is the same. It's just two different ways of writing the same expression. The C# compiler desugars the query-syntax expression to one that composes with SelectMany.
Join #
In the introduction you learned that if you have a Flatten or Join function, you can implement SelectMany, and the other way around. Since we've already defined SelectMany for Maybe<T>, we can use that to implement Join. In this article I use the name Join rather than Flatten. This is an arbitrary choice that doesn't impact behaviour. Perhaps you find it confusing that I'm inconsistent, but I do it in order to demonstrate that the behaviour is the same even if the name is different.
The concept of a monad is universal, but the names used to describe its components differ from language to language. What C# calls SelectMany, Scala calls flatMap, and what Haskell calls join, other languages may call Flatten.
You can always implement Join by using SelectMany with the identity function.
public static Maybe<T> Join<T>(this Maybe<Maybe<T>> source) { return source.SelectMany(x => x); }
Instead of flattening as you go with SelectMany, you could also use Select and Join to compose Average and Sqrt:
[Theory] [InlineData(new double[0], -100)] [InlineData(new double[] { 5, 3 }, 2)] [InlineData(new double[] { 1, -2 }, -100)] public void JoinAverageAndSqrt(double[] values, double expected) { Maybe<double> actual = Average(values).Select(Sqrt).Join(); Assert.Equal(expected, actual.GetValueOrFallback(-100)); }
You'd typically not write the composition like this, as it seems more convenient to use SelectMany, but you could. The behaviour is the same.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. Conceptually, I call this function return (because that's the name that Haskell uses). You don't, however, have to define a static method called Return. What's of importance is that the capability exists. For Maybe<T> in C# the idiomatic way would be to use a constructor. This constructor overload does double duty as monadic return:
public Maybe(T item) { if (item == null) throw new ArgumentNullException(nameof(item)); this.HasItem = true; this.Item = item; }
Why is it that overload, and not the other one? Because if you try to use new Maybe<T>() as return, you'll find that it breaks the monad laws. Try it. It's a good exercise.
Left identity #
Now that we're on the topic of the monad laws, let's see what they look like for the Maybe monad, starting with the left identity law.
[Theory] [InlineData(0)] [InlineData(1)] [InlineData(2)] public void LeftIdentity(int a) { Func<int, Maybe<int>> @return = i => new Maybe<int>(i); Func<int, Maybe<double>> h = i => i != 0 ? new Maybe<double>(1.0 / i) : new Maybe<double>(); Assert.Equal(@return(a).SelectMany(h), h(a)); }
To provide some variety, h is another Maybe-valued function - this time one that performs a safe multiplicative inverse. If i is zero, it returns an empty Maybe<double> because you can't devide by zero; otherwise, it returns one divided by i (wrapped in a Maybe<double>).
Right identity #
In a similar manner, we can showcase the right identity law as a test.
[Theory] [InlineData("")] [InlineData("foo")] [InlineData("42")] [InlineData("1337")] public void RightIdentity(string a) { Maybe<int> f(string s) { if (int.TryParse(s, out var i)) return new Maybe<int>(i); else return new Maybe<int>(); } Func<int, Maybe<int>> @return = i => new Maybe<int>(i); Maybe<int> m = f(a); Assert.Equal(m.SelectMany(@return), m); }
Again, for variety's sake, for f I've chosen a function that should probably be named TryParseInt if used in another context.
Associativity #
The last monad law is the associativity law that we can demonstrate like this:
[Theory] [InlineData("bar")] [InlineData("-1")] [InlineData("0")] [InlineData("4")] public void Associativity(string a) { Maybe<int> f(string s) { if (int.TryParse(s, out var i)) return new Maybe<int>(i); else return new Maybe<int>(); } Func<int, Maybe<double>> g = i => Sqrt(i); Func<double, Maybe<double>> h = d => d == 0 ? new Maybe<double>() : new Maybe<double>(1 / d); var m = f(a); Assert.Equal(m.SelectMany(g).SelectMany(h), m.SelectMany(x => g(x).SelectMany(h))); }
Here, I've copy-and-pasted the TryParseInt function I also used in the right identity example, and combined it with the Sqrt function and a safe multiplicative inverse. The law, however, should hold for all pure functions that type-check. The functions shown here are just examples.
As usual, a parametrised test is no proof that the law holds. I provide the tests only as examples of what the laws looks like.
Conclusion #
The Maybe sum type is a versatile and useful data structure that forms a monad. This enables you to compose disparate functions that each may err by failing to return a value.
Next: An Either monad.
The List monad
Lists, collections, deterministic Iterators form a monad. An article for object-oriented programmers.
This article is an instalment in an article series about monads.
In the article series about functors I never included an explicit article about collections. Instead, I wrote:
"Perhaps the most well-known of all functors is List, a.k.a. Sequence. C# query syntax can handle any functor, but most people only think of it as a language feature related to
IEnumerable<T>. Since the combination ofIEnumerable<T>and query syntax is already well-described, I'm not going to cover it explicitly here."
Like many other useful functors, a list also forms a monad. In this article, I call it list. In Haskell the most readily available equivalent is the built-in linked list ([]). Likewise, in F#, the fundamental collection types are linked lists and arrays. In C#, any IEnumerable<T> forms a monad. The .NET IEnumerable<T> interface is an application of the Iterator design pattern. There are many possible names for this monad: list, sequence, collection, iterator, etcetera. I've arbitrarily chosen to mostly use list.
SelectMany #
In the introduction to monads you learned that monads are characterised by having either a join (or flatten) function, or a bind function. While in Haskell, monadic bind is the >>= operator, in C# it's a method called SelectMany. Perhaps you wonder about the name.
The name SelectMany makes most sense in the context of lists. An example would be useful around here.
Imagine that you have to parse a CSV file. You've already read the file from disc and split the contents into lines. Now you need to split each line on commas.
> var lines = new[] { "foo,bar,baz", "qux,quux,quuz" }; > lines.Select(l => l.Split(',')).ToArray() string[2][] { string[3] { "foo", "bar", "baz" }, string[3] { "qux", "quux", "quuz" } }
When you use Select the result is a nested list. You've already learned that a monad is a functor you can flatten. In C#, you can 'flatten as you go' with SelectMany.
The above scenario offers a hint at why the method is named SelectMany. You use it instead of Select when the selector returns many values. In the above example, the Split method returns many values.
So, instead of Select, use SelectMany if you need a flattened list:
> lines.SelectMany(l => l.Split(',')).ToArray()
string[6] { "foo", "bar", "baz", "qux", "quux", "quuz" }
I've never had the opportunity to ask any of the LINQ designers about that naming choice, but this explanation makes sense to me. Even if it turns out that they had something else in mind when they named the method, I think that my explanation at least serves as a mnemonic device.
The name is still unfortunate, since it mostly makes sense for the list monad. Already when you use SelectMany with the Maybe monad, the name makes less sense.
Flatten #
In the introduction you learned that if you have a Flatten or Join function, you can implement SelectMany, and the other way around. In C#, LINQ already comes with SelectMany, but surprisingly, Flatten isn't built in.
You can always implement Flatten by using SelectMany with the identity function.
public static IEnumerable<T> Flatten<T>(this IEnumerable<IEnumerable<T>> source) { return source.SelectMany(x => x); }
Recall that the selector passed to SelectMany must have the type Func<TSource, IEnumerable<TResult>>. There's no rule, however, that says that TSource can't be IEnumerable<TResult>. If x in x => x has the type IEnumerable<TResult>, then x => x has the type Func<IEnumerable<TResult>, IEnumerable<TResult>> and it all type-checks.
Here's a test that demonstrates how Flatten works:
[Fact] public void FlattenExample() { string[][] nested = new[] { new[] { "foo", "bar" }, new[] { "baz" } }; IEnumerable<string> flattened = nested.Flatten(); Assert.Equal(new[] { "foo", "bar", "baz" }, flattened); }
In Haskell Flatten is called join and is implemented this way:
join :: (Monad m) => m (m a) -> m a join x = x >>= id
It's the same implementation as the above C# method: monadic bind (SelectMany in C#; >>= in Haskell) with the identity function. The Haskell implementation works for all monads.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. For the list monad, this implies a single value promoted to a list. Surprisingly, the .NET base class library doesn't come with such a built-in function, but you can easily implement it yourself:
public static IEnumerable<T> Return<T>(T x) { yield return x; }
In practice, however, you'd normally instead create a singleton array, like this: new[] { 2112 }. Since arrays implement IEnumerable<T>, this works just as well.
Why is this the correct implementation of return?
Wouldn't this work?
public static IEnumerable<T> ReturnZero<T>(T x) { yield break; }
Or this?
public static IEnumerable<T> ReturnTwo<T>(T x) { yield return x; yield return x; }
None of these are appropriate because they break the monad laws. Try it, as an exercise!
Left identity #
Now that we're on the topic of the monad laws, let's see what they look like for the list monad, starting with the left identity law.
[Theory] [InlineData("")] [InlineData("foo")] [InlineData("foo,bar")] [InlineData("foo,bar,baz")] public void LeftIdentity(string a) { Func<string, IEnumerable<string>> @return = List.Return; Func<string, IEnumerable<string>> h = s => s.Split(','); Assert.Equal(@return(a).SelectMany(h), h(a)); }
As usual, a parametrised test is no proof that the law holds. I provide it only as an example of what the law looks like.
Right identity #
Likewise, we can showcase the right identity law as a test:
[Theory] [InlineData(0)] [InlineData(1)] [InlineData(9)] public void RightIdentity(int a) { Func<int, IEnumerable<string>> f = i => Enumerable.Repeat("foo", i); Func<string, IEnumerable<string>> @return = List.Return; IEnumerable<string> m = f(a); Assert.Equal(m.SelectMany(@return), m); }
These tests all pass.
Associativity #
The last monad law is the associativity law that we can demonstrate like this:
[Theory] [InlineData(0)] [InlineData(3)] [InlineData(8)] public void Associativity(int a) { Func<int, IEnumerable<string>> f = i => Enumerable.Repeat("foo", i); Func<string, IEnumerable<char>> g = s => s; Func<char, IEnumerable<string>> h = c => new[] { c.ToString().ToUpper(), c.ToString().ToLower() }; IEnumerable<string> m = f(a); Assert.Equal(m.SelectMany(g).SelectMany(h), m.SelectMany(x => g(x).SelectMany(h))); }
The three functions f, g, and h are just silly functions I chose for variety's sake.
Conclusion #
Lists, arrays, collections, Iterators are various names for a common idea: that of an ordered sequence of values. In this article, I've called it list for simplicity's sake. It's possible to flatten nested lists in a well-behaved manner, which makes list a monad.
Next: The Maybe monad.
Monad laws
An article for object-oriented programmers.
This article is an instalment in an article series about monads.
Just as functors must obey the functor laws, monads must follow the monad laws. When looked at from the right angle, these are intuitive and reasonable rules: identity and associativity.
That sounds almost like a monoid, but the rules are more relaxed. For monoids, we require a binary operation. That's not the case for functors and monads. Instead of binary operations, for monads we're going to use Kleisli composition.
This article draws heavily on the Haskell wiki on monad laws.
In short, the monad laws comprise three rules:
- Left identity
- Right identity
- Associativity
The article describes each in turn, starting with left identity.
Left identity #
A left identity is an element that, when applied to the left of an operator, doesn't change the other element. When used with the fish operator it looks like this:
id >=> h ≡ h
For monads, id turns out to be return, so more specifically:
return >=> h ≡ h
In C# we can illustrate the law as a parametrised test:
[Theory] [InlineData(-1)] [InlineData(42)] [InlineData(87)] public void LeftIdentityKleisli(int a) { Func<int, Monad<int>> @return = Monad.Return; Func<int, Monad<string>> h = i => Monad.Return(i.ToString()); Func<int, Monad<string>> composed = @return.Compose(h); Assert.Equal(composed(a), h(a)); }
Recall that we can implement the fish operators as Compose overloads. The above test demonstrates the notion that @return composed with h should be indistinguishable from h. Such a test should pass.
Keep in mind, however, that Kleisli composition is derived from the definition of a monad. The direct definition of monads is that they come with a return and bind functions (or, alternatively return and join). If we inline the implementation of Compose, the test instead looks like this:
[Theory] [InlineData(-1)] [InlineData(42)] [InlineData(87)] public void LeftIdentityInlined(int a) { Func<int, Monad<int>> @return = Monad.Return; Func<int, Monad<string>> h = i => Monad.Return(i.ToString()); Func<int, Monad<string>> composed = x => @return(x).SelectMany(h); Assert.Equal(composed(a), h(a)); }
or, more succinctly:
Assert.Equal(@return(a).SelectMany(h), h(a));
This is also the way the left identity law is usually presented in Haskell:
return a >>= h = h a
In Haskell, monadic bind is represented by the >>= operator, while in C# it's the SelectMany method. Thus, the Haskell and the C# representations are equivalent.
Right identity #
Right identity starts out similar to left identity. Using the fish operator, the Haskell wiki describes it as:
f >=> return ≡ f
Translated to a C# test, an example of that law might look like this:
[Theory] [InlineData("foo")] [InlineData("ploeh")] [InlineData("lawful")] public void RightIdentityKleisli(string a) { Func<string, Monad<int>> f = s => Monad.Return(s.Length); Func<int, Monad<int>> @return = Monad.Return; Func<string, Monad<int>> composed = f.Compose(@return); Assert.Equal(composed(a), f(a)); }
Again, if we inline Compose, the test instead looks like this:
[Theory] [InlineData("foo")] [InlineData("ploeh")] [InlineData("lawful")] public void RightIdentityInlined(string a) { Func<string, Monad<int>> f = s => Monad.Return(s.Length); Func<int, Monad<int>> @return = Monad.Return; Func<string, Monad<int>> composed = x => f(x).SelectMany(@return); Assert.Equal(composed(a), f(a)); }
Now explicitly call the f function and assign it to a variable m:
[Theory] [InlineData("foo")] [InlineData("ploeh")] [InlineData("lawful")] public void RightIdentityInlinedIntoAssertion(string a) { Func<string, Monad<int>> f = s => Monad.Return(s.Length); Func<int, Monad<int>> @return = Monad.Return; Monad<int> m = f(a); Assert.Equal(m.SelectMany(@return), m); }
The assertion is now the C# version of the normal Haskell definition of the right identity law:
m >>= return = m
In other words, return is the identity element for monadic composition. It doesn't really 'do' anything in itself.
Associativity #
The third monad law is the associativity law. Keep in mind that an operator like + is associative if it's true that
(x + y) + z = x + (y + z)
Instead of +, the operator in question is the fish operator, and since values are functions, we typically call them f, g, and h rather than x, y, and z:
(f >=> g) >=> h ≡ f >=> (g >=> h)
Translated to a C# test as an example, the law looks like this:
[Theory] [InlineData(0)] [InlineData(1)] [InlineData(2)] public void AssociativityKleisli(double a) { Func<double, Monad<bool>> f = i => Monad.Return(i % 2 == 0); Func<bool, Monad<string>> g = b => Monad.Return(b.ToString()); Func<string, Monad<int>> h = s => Monad.Return(s.Length); Func<double, Monad<int>> left = (f.Compose(g)).Compose(h); Func<double, Monad<int>> right = f.Compose(g.Compose(h)); Assert.Equal(left(a), right(a)); }
The outer brackets around (f.Compose(g)) are actually redundant; we should remove them. Also, inline Compose:
[Theory] [InlineData(0)] [InlineData(1)] [InlineData(2)] public void AssociativityInlined(double a) { Func<double, Monad<bool>> f = i => Monad.Return(i % 2 == 0); Func<bool, Monad<string>> g = b => Monad.Return(b.ToString()); Func<string, Monad<int>> h = s => Monad.Return(s.Length); Func<double, Monad<string>> fg = x => f(x).SelectMany(g); Func<double, Monad<int>> left = x => fg(x).SelectMany(h); Func<bool, Monad<int>> gh = x => g(x).SelectMany(h); Func<double, Monad<int>> right = x => f(x).SelectMany(gh); Assert.Equal(left(a), right(a)); }
If there's a way in C# to inline the local compositions fg and gh directly into left and right, respectively, I don't know how. In any case, the above is just an intermediate step.
For both left and right, notice that the first step involves invoking f with x. If, instead, we call that value m, we can rewrite the test like this:
[Theory] [InlineData(0)] [InlineData(1)] [InlineData(2)] public void AssociativityInlinedIntoAssertion(double a) { Func<double, Monad<bool>> f = i => Monad.Return(i % 2 == 0); Func<bool, Monad<string>> g = b => Monad.Return(b.ToString()); Func<string, Monad<int>> h = s => Monad.Return(s.Length); Monad<bool> m = f(a); Assert.Equal(m.SelectMany(g).SelectMany(h), m.SelectMany(x => g(x).SelectMany(h))); }
The above assertion corresponds to the way the associativity law is usually represented in Haskell:
(m >>= g) >>= h = m >>= (\x -> g x >>= h)
Once more, keep in mind that >>= in Haskell corresponds to SelectMany in C#.
Conclusion #
A proper monad must satisfy the three monad laws: left identity, right identity, and associativity. Together, left identity and right identity are know as simply identity. What's so special about identity and associativity?
As Bartosz Milewski explains, a category must satisfy associativity and identity. When it comes to monads, the category in question is the Kleisli category. Or, as the Haskell wiki puts it:
Monad axioms:
Kleisli composition forms
a category.
Subsequent articles in this article series will now proceed to give examples of concrete monads, and what the laws look like for each of these.
Next: The List monad.
Comments
That sounds almost like a monoid, but the rules are more relaxed. For monoids, we require a binary operation. That's not the case for functors and monads. Instead of binary operations, for monads we're going to use Kleisli composition.
I am confused by this paragraph. A monoid requries a binary operation (that is also closed), and Kleisli composition is (closed) binary operation.
As you said in the introductory article to this monad series, there are three pieces to a monad: a generic type M<>, a function with type a -> M<a> (typically called "return"), and a function with signature (a -> M<b>) -> M<a> -> M<b> (sometimes called "bind"). Then (M<>, return, bind) is a monad if those three items satisfy the monad laws.
I think the following is true. Let M<> be a generic type, and let S be the set of all functions with signature a -> M<a>. Then (M<>, return, bind) is a monad if only only if (S, >=>, return) is a monoid.
Tyson, thank you for writing. To address the elephant in the room first: A monad is a monoid (in the category of endofunctors), but as far as I can tell, you have to look more abstractly at it than allowed by the static type systems we normally employ.
Bartosz Milewski describes a nested functor as the tensor product of two monadic types: M ⊗ M. The binary operation in question is then M ⊗ M -> M, or join/flatten (from here on just join). In this very abstract view, monads are monoids. It does require an abstract view of functors as objects in a category. At that level of abstraction, so many details are lost that join looks like a binary operation.
So, to be clear, if you want to look at a monad as a monoid, it's not the monadic bind function that's the binary operation; it's join. (That's another reason I prefer explaining monads in terms of join rather than leading with bind.)
When you zoom in on the details, however, join doesn't look like a regular binary operation: m (m a) -> m a. A binary operation, on the other hand, should look like this: m a -> m a -> m a.
The Kleisli composition operator unfortunately doesn't fix this. Let's look at the C# method signature, since it may offer a way out:
public static Func<T, Monad<T2>> Compose<T, T1, T2>( Func<T, Monad<T1>> action1, Func<T1, Monad<T2>> action2)
Notice that the types don't match: action1 has a type different from action2, which is again different from the return type. Thus, it's not a binary operation, because the elements don't belong to the same set.
As Bartosz Milewski wrote, though, if we squint a little, we may make it work. C# allows us to 'squint' because of its object hierarchy:
public static Func<object, Monad<object>> Compose( Func<object, Monad<object>> action1, Func<object, Monad<object>> action2)
I'm not sure how helpful that is, though, so I didn't want to get into these weeds in the above article itself. It's fine here in the comments, because I expect only very dedicated readers to consult them. This, thus, serves more like a footnote or appendix.
Thanks very much for you reply. It helped me to see where I was wrong. (S, >=>, return) is not a monoid because >=> is not total over S, which is another condition the binary operation must satisfy, but I overlooked that. Furthremore, I meant to define S as the set of all functions with signature a -> M<b>. The same problem still exists though. The second code block in your comment has this same problem. There is not a natural choice for the implementation unless the types of the objects satisfy the constraints implied by the use of type parameters in the first code block in your comment. I will keep thinking about this.
In the meantime, keep up the great work. I am loving your monad content.

Comments
I often want run selected tests from the command line and thus use the test runner's abilty to filter all available tests. Where the set of tests I want to run is all the tests below some point in the heirarchy of tests I can filter by the common prefix, or the test class name.
But I also often find myself wanting to run a set of tests that meet some functional criteria, e.g Validation approval tests, or All the tests for a particular feature across all the levels of the code base. In this case if the tests follow a naming convention where such test attributes are included in the test name, either via the method or class name, then such test filtering is possible.
Mark, are you a Classicist or a Mockist? I'm going to go out on a limb here and say you're probably a classicist. Test code written in a classicist style probably conveys the intent well already. I think code written in a Mockist style may not convey the intent as well, hence the test name (or a comment) becomes more useful to convey that information.
There are (at least) two ways of using test names (as well as test module names, as suggested by Struan Judd) that we make extensive use of in the LinkedIn code base and which I have used in every code base I have ever written tests for:
To indicate the intent of the test. It is well and good to say that the assertions should convey the conditions, but often it is not clear why a condition is intended to hold. Test names (and descriptive strings on the assertions) can go a very long way, especially when working in a large and/or unfamiliar code base, to understand whether the assertion remains relevant, or how it is relevant.
Now, granted: it is quite possible for those to get out of date, much as comments do. However, just as good comments remain valuable even though there is a risk of stale comments, good test names can be valuable even though they can also become stale.
The key, for me, is exactly the same as good comments—and you could argue that comments therefore obviate the need for test names. If we only cared about tests from the POV of reading the code, I would actually agree! However, because we often read the tests as a suite of assertions presented in some other UI (a terminal, a web view, etc.), the names and assertion descriptions themselves serve as the explanation when reading.
To provide structure and organization to the test suite. This is the same point Struan Judd was getting at: having useful test names lets you filter down to relevant chunks of the suite easily. This is valuable even on a small code base (like the
MaybeandResultlibrary in TypeScript a friend and I maintain), but it becomes invaluable when you have tens of thousands of tests to filter or search through, as in the main LinkedIn app!For that reason, we (and the Ember.js community more broadly) make extensive use of QUnit's
module()hook to name the set of modules under test (module('Rendering | SomeComponent', function () { ... }ormodule('Unit | some-utility', function () { ... }) as well as namingtest()(test('returns `null` if condition X does not hold', function (assert) { ... }) and indeed providing descriptive strings forassert()calls. We might even nestmodule()calls to make it easy to see and filter from how our test UI presents things: Rendering | SomeComponent > someMethod > a test description.Now, how that plays out varies library to library. The aforementioned TS library just names the test with a decent description of what is under test (here, for example) as well as grouping them sensibly with overarching descriptions, and never uses assertion descriptions because they wouldn’t add anything. A couple of the libraries I wrote internally at LinkedIn, by contrast, make extensive use of both. It is, as usual, a tool to be employed as, and only as, it is useful. But it is indeed quite useful sometimes!
Struan, thank you for writing. I can't say that I've given much thought to the need to run subsets of a test suite. You have a point, though, that if that's a requirement, you need something on which to filter.
Is the name the appropriate criterion for that, though? It sounds brittle to me, but I grant that it depends on which alternatives are available. In xUnit.net, for example, you can use the
[Trait]attribute to annotate tests with arbitrary metadata. I think that NUnit has a similar feature, but there's no guarantee that every unit testing framework on any platform or language supports such a feature.Whenever a framework supports such metadata-based filtering, I'd favour relying on that instead of naming conventions. Naming conventions are vulnerable to misspellings and other programmer errors. That may also be true of metadata-based categorisation, but hopefully to a lesser degree, as these might enable you to use ordinary language features to keep the categories DRY.
Using names also sounds restrictive to me. Doesn't this mean that you have to be able to predict your filtering requirements when you decide on a naming scheme?
What if, later, you find that you need to filter on a different dimension? With metadata annotations, you should be able to add a new category to the affected tests, but how will you do that with an established naming scheme?
Overall, though, the reason that I haven't given this much thought is that I've never had the need to filter tests in arbitrary ways. You must be doing something different from how I work with tests. Why do you need to filter tests?
Eddie, thank you for writing. I don't find the linked article illuminating if one hasn't already heard about the terms mockist and classicist. I rather prefer the terms interaction-based and state-based testing. In any case, I started out doing interaction-based testing, but have since moved away from that. Even when I mainly wrote interaction-based tests, though, I didn't like rigid naming schemes. I don't see how that makes much of a difference.
I agree that a test name is a fine opportunity to convey intent. Did that not come across in the article?
Chris, thank you for writing. As I also responded to Eddie Stanley, I agree that a test name is a fine opportunity to convey intent. Did that not come across in the article?
To your second point, I'll refer you to my answer to Struan Judd. I'm still curious to learn why you find it necessary to categorise and filter tests.