ploeh blog danish software design
Warnings-as-errors friction
TDD friction. Surely that's a bad thing(?)
Paul Wilson recently wrote on Mastodon:
Software development opinion (warnings as errors)
Just seen this via Elixir Radar, https://curiosum.com/til/warnings-as-errors-elixir-mix-compile on on treating warnings as errors, and yeah don't integrate code with warnings. But ....
Having worked on projects with this switched on in dev, it's an annoying bit of friction when Test Driving code. Yes, have it switched on in CI, but don't make me fix all the warnings before I can run my failing test.
(Using an env variable for the switch is a good compromise here, imo).
This made me reflect on similar experiences I've had. I thought perhaps I should write them down.
To be clear, this article is not an attack on Paul Wilson. He's right, but since he got me thinking, I only find it honest and respectful to acknowledge that.
The remark does, I think, invite more reflection.
Test friction example #
An example would be handy right about now.
As I was writing the example code base for Code That Fits in Your Head, I was following the advice of the book:
- Turn on Nullable reference types (only relevant for C#)
- Turn on static code analysis or linters
- Treat warnings as errors. Yes, also the warnings produced by the two above steps
As Paul Wilson points out, this tends to create friction with test-driven development (TDD). When I started the code base, this was the first TDD test I wrote:
[Fact] public async Task PostValidReservation() { var response = await PostReservation(new { date = "2023-03-10 19:00", email = "katinka@example.com", name = "Katinka Ingabogovinanana", quantity = 2 }); Assert.True( response.IsSuccessStatusCode, $"Actual status code: {response.StatusCode}."); }
Looks good so far, doesn't it? Are any of the warnings-as-errors settings causing friction? Not directly, but now regard the PostReservation helper method:
[SuppressMessage( "Usage", "CA2234:Pass system uri objects instead of strings", Justification = "URL isn't passed as variable, but as literal.")] private async Task<HttpResponseMessage> PostReservation( object reservation) { using var factory = new WebApplicationFactory<Startup>(); var client = factory.CreateClient(); string json = JsonSerializer.Serialize(reservation); using var content = new StringContent(json); content.Headers.ContentType.MediaType = "application/json"; return await client.PostAsync("reservations", content); }
Notice the [SuppressMessage] attribute. Without it, the compiler emits this error:
error CA2234: Modify 'ReservationsTests.PostReservation(object)' to call 'HttpClient.PostAsync(Uri, HttpContent)' instead of 'HttpClient.PostAsync(string, HttpContent)'.
That's an example of friction in TDD. I could have fixed the problem by changing the last line to:
return await client.PostAsync(new Uri("reservations", UriKind.Relative), content);
This makes the actual code more obscure, which is the reason I didn't like that option. Instead, I chose to add the [SuppressMessage] attribute and write a Justification. It is, perhaps, not much of an explanation, but my position is that, in general, I consider CA2234 a good and proper rule. It's a specific example of favouring stronger types over stringly typed code. I'm all for it.
If you grok the motivation for the rule (which, evidently, the documentation code-example writer didn't) you also know when to safely ignore it. Types are useful because they enable you to encapsulate knowledge and guarantees about data in a way that strings and ints typically don't. Indeed, if you are passing URLs around, pass them around as Uri objects rather than strings. This prevents simple bugs, such as accidentally swapping the place of two variables because they're both strings.
In the above example, however, a URL isn't being passed around as a variable. The value is hard-coded right there in the code. Wrapping it in a Uri object doesn't change that.
But I digress...
This is an example of friction in TDD. Instead of being able to just plough through, I had to stop and deal with a Code Analysis rule.
SUT friction example #
But wait! There's more.
To pass the test, I had to add this class:
[Route("[controller]")] public class ReservationsController { #pragma warning disable CA1822 // Mark members as static public void Post() { } #pragma warning restore CA1822 // Mark members as static }
I had to suppress CA1822 as well, because it generated this error:
error CA1822: Member Post does not access instance data and can be marked as static (Shared in VisualBasic)
Keep in mind that because of my settings, it's an error. The code doesn't compile.
You can try to fix it by making the method static, but this then triggers another error:
error CA1052: Type 'ReservationsController' is a static holder type but is neither static nor NotInheritable
In other words, the class should be static as well:
[Route("[controller]")] public static class ReservationsController { public static void Post() { } }
This compiles. What's not to like? Those Code Analysis rules are there for a reason, aren't they? Yes, but they are general rules that can't predict every corner case. While the code compiles, the test fails.
Out of the box, that's just not how that version of ASP.NET works. The MVC model of ASP.NET expects action methods to be instance members.
(I'm sure that there's a way to tweak ASP.NET so that it allows static HTTP handlers as well, but I wasn't interested in researching that option. After all, the above code only represents an interim stage during a longer TDD session. Subsequent tests would prompt me to give the Post method some proper behaviour that would make it an instance method anyway.)
So I kept the method as an instance method and suppressed the Code Analysis rule.
Friction? Demonstrably.
Opt in #
Is there a way to avoid the friction? Paul Wilson mentions a couple of options: Using an environment variable, or only turning warnings into errors in your deployment pipeline. A variation on using an environment variable is to only turn on errors for Release builds (for languages where that distinction exists).
In general, if you have a useful tool that unfortunately takes a long time to run, making it a scheduled or opt-in tool may be the way to go. A mutation testing tool like Stryker can easily run for hours, so it's not something you want to do for every change you make.
Another example is dependency analysis. One of my recent clients had a tool that scanned their code dependencies (NuGet, npm) for versions with known vulnerabilities. This tool would also take its time before delivering a verdict.
Making tools opt-in is definitely an option.
You may be concerned that this requires discipline that perhaps not all developers have. If a tool is opt-in, will anyone remember to run it?
As I also describe in Code That Fits in Your Head, you could address that issue with a checklist.
Yeah, but do we then need a checklist to remind us to look at the checklist? Right, quis custodiet ipsos custodes? Is it going to be turtles all the way down?
Well, if no-one in your organisation can be trusted to follow any commonly-agreed-on rules on a regular basis, you're in trouble anyway.
Good friction? #
So far, I've spent some time describing the problem. When encountering resistance your natural reaction is to find it disagreeable. You want to accomplish something, and then this rule/technique/tool gets in the way!
Despite this, is it possible that this particular kind of friction is beneficial?
By (subconsciously, I'm sure) picking a word like 'friction', you've already chosen sides. That word, in general, has a negative connotation. Is it the only word that describes the situation? What if we talked about it instead in terms of safety, assistance, or predictability?
Ironically, friction was a main complaint about TDD when it was first introduced.
"What do you mean? I have to write a test before I write the implementation? That's going to slow me down!"
The TDD and agile movement developed a whole set of standard responses to such objections. Brakes enable you to go faster. If it hurts, do it more often.
Try those on for size, only now applied to warnings as errors. Friction is what makes brakes work.
Additive mindset #
As I age, I'm becoming increasingly aware of a tendency in the software industry. Let's call it the additive mindset.
It's a reflex to consider addition a good thing. An API with a wide array of options is better than a narrow API. Software with more features is better than software with few features. More log data provides better insight.
More code is better than less code.
Obviously, that's not true, but we. keep. behaving as though it is. Just look at the recent hubbub about ChatGPT, or GitHub Copilot, which I recently wrote about. Everyone reflexively view them as productivity tools because the can help us produce more code faster.
I had a cup of coffee with my wife as I took a break from writing this article, and I told her about it. Her immediate reaction when told about friction is that it's a benefit. She's a doctor, and naturally view procedure, practice, regulation, etcetera as occasionally annoying, but essential to the practice of medicine. Without procedures, patients would die from preventable mistakes and doctors would prescribe morphine to themselves. Checking boxes and signing off on decisions slow you down, and that's half the point. Making you slow down can give you the opportunity to realise that you're about to do something stupid.
Worried that TDD will slow down your programmers? Don't. They probably need slowing down.
But if TDD is already being touted as a process to make us slow down and think, is it a good idea, then, to slow down TDD with warnings as errors? Are we not interfering with a beneficial and essential process?
Alternatives to TDD #
I don't have a confident answer to that question. What follows is tentative. I've been doing TDD since 2003 and while I was also an early critic, it's still central to how I write code.
When I began doing TDD with all the errors dialled to 11 I was concerned about the friction, too. While I also believe in linters, the two seem to work at cross purposes. The rule about static members in the above example seems clearly counterproductive. After all, a few commits later I'd written enough code for the Post method that it had to be an instance method after all. The degenerate state was temporary, an artefact of the TDD process, but the rule triggered anyway.
What should I think of that?
I don't like having to deal with such false positives. The question is whether treating warnings as errors is a net positive or a net negative?
It may help to recall why TDD is a useful practice. A major reason is that it provides rapid feedback. There are, however, other ways to produce rapid feedback. Static types, compiler warnings, and static code analysis are other ways.
I don't think of these as alternatives to TDD, but rather as complementary. Tests can produce feedback about some implementation details. Constructive data is another option. Compiler warnings and linters enter that mix as well.
Here I again speak with some hesitation, but it looks to me as though the TDD practice originated in dynamically typed tradition (Smalltalk), and even though some Java programmers were early adopters as well, from my perspective it's always looked stronger among the dynamic languages than the compiled languages. The unadulterated TDD tradition still seems to largely ignore the existence of other forms of feedback. Everything must be tested.
At the risk of repeating myself, I find TDD invaluable, but I'm happy to receive rapid feedback from heterogeneous sources: Tests, type checkers, compilers, linters, fellow ensemble programmers.
This suggests that TDD isn't the only game in town. This may also imply that the friction to TDD caused by treating warnings as errors may not be as costly as first perceived. After all, slowing down something that you rely on 75% of the time isn't quite as bad as slowing down something you rely on 100% of the time.
While it's a cost, perhaps it went down...
Simplicity #
As always, circumstances matter. Is it always a good idea to treat warnings as errors?
Not really. To be honest, treating warnings as errors is another case of treating a symptom. The reason I recommend it is that I've seen enough code bases where compiler warnings (not errors) have accumulated. In a setting where that happens, treating (new) warnings as errors can help get the situation under control.
When I work alone, I don't allow warnings to build up. I rarely tell the compiler to treat warnings as errors in my personal code bases. There's no need. I have zero tolerance for compiler warnings, and I do spot them.
If you have a team that never allows compiler warnings to accumulate, is there any reason to treat them as errors? Probably not.
This underlines an important point about productivity: A good team without strict process can outperform a poor team with a clearly defined process. Mindset beats tooling. Sometimes.
Which mindset is that? Not the additive mindset. Rather, I believe in focusing on simplicity. The alternative to adding things isn't to blindly remove things. You can't add features to a program only by deleting code. Rather, add code, but keep it simple. Decouple to delete.
perfection is attained not when there is nothing more to add, but when there is nothing more to remove.
Simple code. Simple tests. Be warned, however, that code simplicity does not imply naive code understandable by everyone. I'll refer you to Rich Hickey's wonderful talk Simple Made Easy and remind you that this was the line of thinking that lead to Clojure.
Along the same lines, I tend to consider Haskell to be a vehicle for expressing my thoughts in a simpler way than I can do in F#, which again enables simplicity not available in C#. Simpler, not easier.
Conclusion #
Does treating warnings as errors imply TDD friction? It certainly looks that way.
Is it worth it, nonetheless? Possibly. It depends on why you need to turn warnings into errors in the first place. In some settings, the benefits of treating warnings as errors may be greater than the cost. If that's the only way you can keep compiler warnings down, then do treat warnings as errors. Such a situation, however, is likely to be a symptom of a more fundamental mindset problem.
This almost sounds like a moral judgement, I realise, but that's not my intent. Mindset is shaped by personal preference, but also by organisational and peer pressure, as well as knowledge. If you only know of one way to achieve a goal, you have no choice. Only if you know of more than one way can you choose.
Choose the way that leaves the code simpler than the other.
Test Data Generator monad
With examples in C# and F#.
This article is an instalment in an article series about monads. In other related series previous articles described Test Data Generator as a functor, as well as Test Data Generator as an applicative functor. As is the case with many (but not all) functors, this one also forms a monad.
This article expands on the code from the above-mentioned articles about Test Data Generators. Keep in mind that the code is a simplified version of what you'll find in a real property-based testing framework. It lacks shrinking and referentially transparent (pseudo-)random value generation. Probably more things than that, too.
SelectMany #
A monad must define either a bind or join function. In C#, monadic bind is called SelectMany. For the Generator<T> class, you can implement it as an instance method like this:
public Generator<TResult> SelectMany<TResult>(Func<T, Generator<TResult>> selector) { Func<Random, TResult> newGenerator = r => { Generator<TResult> g = selector(generate(r)); return g.Generate(r); }; return new Generator<TResult>(newGenerator); }
SelectMany enables you to chain generators together. You'll see an example later in the article.
Query syntax #
As the monad article explains, you can enable C# query syntax by adding a special SelectMany overload:
public Generator<TResult> SelectMany<U, TResult>( Func<T, Generator<U>> k, Func<T, U, TResult> s) { return SelectMany(x => k(x).Select(y => s(x, y))); }
The implementation body always looks the same; only the method signature varies from monad to monad. Again, I'll show you an example of using query syntax later in the article.
Flatten #
In the introduction you learned that if you have a Flatten or Join function, you can implement SelectMany, and the other way around. Since we've already defined SelectMany for Generator<T>, we can use that to implement Flatten. In this article I use the name Flatten rather than Join. This is an arbitrary choice that doesn't impact behaviour. Perhaps you find it confusing that I'm inconsistent, but I do it in order to demonstrate that the behaviour is the same even if the name is different.
public static Generator<T> Flatten<T>(this Generator<Generator<T>> generator) { return generator.SelectMany(x => x); }
As you can tell, this function has to be an extension method, since we can't have a class typed Generator<Generator<T>>. As usual, when you already have SelectMany, the body of Flatten (or Join) is always the same.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. Conceptually, I call this function return (because that's the name that Haskell uses):
public static Generator<T> Return<T>(T value) { return new Generator<T>(_ => value); }
This function ignores the random number generator and always returns value.
Left identity #
We needed to identify the return function in order to examine the monad laws. Let's see what they look like for the Test Data Generator monad, starting with the left identity law.
[Theory] [InlineData(17, 0)] [InlineData(17, 8)] [InlineData(42, 0)] [InlineData(42, 1)] public void LeftIdentityLaw(int x, int seed) { Func<int, Generator<string>> h = i => new Generator<string>(r => r.Next(i).ToString()); Assert.Equal( Generator.Return(x).SelectMany(h).Generate(new Random(seed)), h(x).Generate(new Random(seed))); }
Notice that the test can't directly compare the two generators, because equality isn't clearly defined for that class. Instead, the test has to call Generate in order to produce comparable values; in this case, strings.
Since Generate is non-deterministic, the test has to seed the random number generator argument in order to get reproducible results. It can't even declare one Random object and share it across both method calls, since generating values changes the state of the object. Instead, the test has to generate two separate Random objects, one for each call to Generate, but with the same seed.
Right identity #
In a manner similar to above, we can showcase the right identity law as a test.
[Theory] [InlineData('a', 0)] [InlineData('a', 8)] [InlineData('j', 0)] [InlineData('j', 5)] public void RightIdentityLaw(char letter, int seed) { Func<char, Generator<string>> f = c => new Generator<string>(r => new string(c, r.Next(100))); Generator<string> m = f(letter); Assert.Equal( m.SelectMany(Generator.Return).Generate(new Random(seed)), m.Generate(new Random(seed))); }
As always, even a parametrised test constitutes no proof that the law holds. I show the tests to illustrate what the laws look like in 'real' code.
Associativity #
The last monad law is the associativity law that describes how (at least) three functions compose. We're going to need three functions. For the demonstration test I'm going to conjure three nonsense functions. While this may not be as intuitive, it on the other hand reduces the noise that more realistic code tends to produce. Later in the article you'll see a more realistic example.
[Theory] [InlineData('t', 0)] [InlineData('t', 28)] [InlineData('u', 0)] [InlineData('u', 98)] public void AssociativityLaw(char a, int seed) { Func<char, Generator<string>> f = c => new Generator<string>(r => new string(c, r.Next(100))); Func<string, Generator<int>> g = s => new Generator<int>(r => r.Next(s.Length)); Func<int, Generator<TimeSpan>> h = i => new Generator<TimeSpan>(r => TimeSpan.FromDays(r.Next(i))); Generator<string> m = f(a); Assert.Equal( m.SelectMany(g).SelectMany(h).Generate(new Random(seed)), m.SelectMany(x => g(x).SelectMany(h)).Generate(new Random(seed))); }
All tests pass.
CPR example #
Formalities out of the way, let's look at a more realistic example. In the article about the Test Data Generator applicative functor you saw an example of parsing a Danish personal identification number, in Danish called CPR-nummer (CPR number) for Central Person Register. (It's not a register of central persons, but rather the central register of persons. Danish works slightly differently than English.)
CPR numbers have a simple format: DDMMYY-SSSS, where the first six digits indicate a person's birth date, and the last four digits are a sequence number. An example could be 010203-1234, which indicates a woman born February 1, 1903.
In C# you might model a CPR number as a class with a constructor like this:
public CprNumber(int day, int month, int year, int sequenceNumber) { if (year < 0 || 99 < year) throw new ArgumentOutOfRangeException( nameof(year), "Year must be between 0 and 99, inclusive."); if (month < 1 || 12 < month) throw new ArgumentOutOfRangeException( nameof(month), "Month must be between 1 and 12, inclusive."); if (sequenceNumber < 0 || 9999 < sequenceNumber) throw new ArgumentOutOfRangeException( nameof(sequenceNumber), "Sequence number must be between 0 and 9999, inclusive."); var fourDigitYear = CalculateFourDigitYear(year, sequenceNumber); var daysInMonth = DateTime.DaysInMonth(fourDigitYear, month); if (day < 1 || daysInMonth < day) throw new ArgumentOutOfRangeException( nameof(day), $"Day must be between 1 and {daysInMonth}, inclusive."); this.day = day; this.month = month; this.year = year; this.sequenceNumber = sequenceNumber; }
The system has been around since 1968 so clearly suffers from a Y2k problem, as years are encoded with only two digits. The workaround for this is that the most significant digit of the sequence number encodes the century. At the time I'm writing this, the Danish-language wikipedia entry for CPR-nummer still includes a table that shows how one can derive the century from the sequence number. This enables the CPR system to handle birth dates between 1858 and 2057.
The CprNumber constructor has to consult that table in order to determine the century. It uses the CalculateFourDigitYear function for that. Once it has the four-digit year, it can use the DateTime.DaysInMonth method to determine the number of days in the given month. This is used to validate the day parameter.
The previous article showed a test that made use of a Test Data Generator for the CprNumber class. The generator was referenced as Gen.CprNumber, but how do you define such a generator?
CPR number generator #
The constructor arguments for month, year, and sequenceNumber are easy to generate. You need a basic generator that produces values between two boundaries. Both QuickCheck and FsCheck call it choose, so I'll reuse that name:
public static Generator<int> Choose(int min, int max) { return new Generator<int>(r => r.Next(min, max + 1)); }
The choose functions of QuickCheck and FsCheck consider both boundaries to be inclusive, so I've done the same. That explains the + 1, since Random.Next excludes the upper boundary.
You can now combine choose with DateTime.DaysInMonth to generate a valid day:
public static Generator<int> Day(int year, int month) { var daysInMonth = DateTime.DaysInMonth(year, month); return Gen.Choose(1, daysInMonth); }
Let's pause and consider the implications. The point of this example is to demonstrate why it's practically useful that Test Data Generators are monads. Keep in mind that monads are functors you can flatten. When do you need to flatten a functor? Specifically, when do you need to flatten a Test Data Generator? Right now, as it turns out.
The Day method returns a Generator<int>, but where do the year and month arguments come from? They'll typically be produced by another Test Data Generator such as choose. Thus, if you only map (Select) over previous Test Data Generators, you'll produce a Generator<Generator<int>>:
Generator<int> genYear = Gen.Choose(1970, 2050); Generator<int> genMonth = Gen.Choose(1, 12); Generator<(int, int)> genYearAndMonth = genYear.Apply(genMonth); Generator<Generator<int>> genDay = genYearAndMonth.Select(t => Gen.Choose(1, DateTime.DaysInMonth(t.Item1, t.Item2)));
This example uses an Apply overload to combine genYear and genMonth. As long as the two generators are independent of each other, you can use the applicative functor capability to combine them. When, however, you need to produce a new generator from a value produced by a previous generator, the functor or applicative functor capabilities are insufficient. If you try to use Select, as in the above example, you'll produce a nested generator.
Since it's a monad, however, you can Flatten it:
Generator<int> flattened = genDay.Flatten();
Or you can use SelectMany (monadic bind) to flatten as you go. The CprNumber generator does that, although it uses query syntax syntactic sugar to make the code more readable:
public static Generator<CprNumber> CprNumber => from sequenceNumber in Gen.Choose(0, 9999) from year in Gen.Choose(0, 99) from month in Gen.Choose(1, 12) let fourDigitYear = TestDataBuilderFunctor.CprNumber.CalculateFourDigitYear(year, sequenceNumber) from day in Gen.Day(fourDigitYear, month) select new CprNumber(day, month, year, sequenceNumber);
The expression first uses Gen.Choose to produce three independent int values: sequenceNumber, year, and month. It then uses the CalculateFourDigitYear function to look up the proper century based on the two-digit year and the sequenceNumber. With that information it can call Gen.Day, and since the expression uses monadic composition, it's flattening as it goes. Thus day is an int value rather than a generator.
Finally, the entire expression can compose the four int values into a valid CprNumber object.
You can consult the previous article to see Gen.CprNumber in use.
Hedgehog CPR generator #
You can reproduce the CPR example in F# using one of several property-based testing frameworks. In this example, I'll continue the example from the previous article as well as the article Danish CPR numbers in F#. You can see a couple of tests in these articles. They use the cprNumber generator, but never show the code.
In all the property-based testing frameworks I've seen, generators are called Gen. This is also the case for Hedgehog. The Gen container is a monad, and there's a gen computation expression that supplies syntactic sugar.
You can translate the above example to a Hedgehog Gen value like this:
let cprNumber = gen { let! sequenceNumber = Range.linear 0 9999 |> Gen.int32 let! year = Range.linear 0 99 |> Gen.int32 let! month = Range.linear 1 12 |> Gen.int32 let fourDigitYear = Cpr.calculateFourDigitYear year sequenceNumber let daysInMonth = DateTime.DaysInMonth (fourDigitYear, month) let! day = Range.linear 1 daysInMonth |> Gen.int32 return Cpr.tryCreate day month year sequenceNumber } |> Gen.some
To keep the example simple, I haven't defined an explicit day generator, but instead just inlined DateTime.DaysInMonth.
Consult the articles that I linked above to see the Gen.cprNumber generator in use.
Conclusion #
Test Data Generators form monads. This is useful when you need to generate test data that depend on other generated test data. Monadic bind (SelectMany in C#) can flatten the generator functor as you go. This article showed examples in both C# and F#.
The same abstraction also exists in the Haskell QuickCheck library, but I haven't shown any Haskell examples. If you've taken the trouble to learn Haskell (which you should), you already know what a monad is.
Next: Functor relationships.
A thought on workplace flexibility and asynchrony
Is an inclusive workplace one that enables people to work at different hours?
In the early noughties I worked for Microsoft Consulting Service in Denmark. In some sense it was quite the competitive working environment with an unhealthy focus on billable hours, customer satisfaction surveys, and stack ranking. On the other hand, since I was mostly on my own on customer engagements, my managers didn't care when and how I worked. As long as I billed and customers were happy, they were happy.
That sometimes allowed me great flexibility.
At one time I was on a project for a customer in another part of Denmark, and while Denmark isn't that big, it was still understood that I would do most of my work remotely. The main deliverable was the code base for a software system, and while I might email and otherwise communicate with the customer and a few colleagues during the day, we didn't have any fixed schedules. In other words, I could work whenever I wanted, as long as I got the work done.
My daughter was a toddler at the time, and as is the norm in Denmark, already in day nursery. My wife is a doctor and was, at that time, working in hospitals - some of the most inflexible workplaces I can think of. She had to leave early in the morning because the hospitals run on fixed schedules.
I'd get up to have breakfast with her. After she left for work, I'd work until my daughter woke up. She typically woke up between 8 and 9, so I'd already be 1-2 hours into my work day. I'd stop working, make her breakfast, and take her to day care. We'd typically arrive between 10 and 11 in good spirits. I'd then bicycle home and work until my wife came home with our daughter. Perhaps I'd get a few more hours of work done in the evening.
I worked odd hours, and I loved the flexibility. My customers expected me to deliver iterations of the software and generally stay in touch, but they were perfectly happy with mostly asynchronous communication. Back then, it mostly meant email.
During the normal work day, I might be unavailable for hours, taking care of my daughter, exercising, grocery shopping, etc. Yet, I still billed more hours than most of my colleagues, and ultimately received an award for my work.
In the decades that followed, I haven't always had such flexibility, but that early experience gave me a strong appreciation for asynchronous work.
Lockdown work wasn't flexible #
When COVID-19 hit and most countries went into lockdown, many office workers got their first taste of remote work. Many struggled, for a variety of reasons. Some of those reasons are quite real. If you don't have a well-equipped home office, spending eight hours a day on a kitchen chair is hardly ideal working conditions. And no, the sofa isn't a good long-term solution either.
Another problem during lockdown is that your entire family may be home, too. If you have kids, you'll have to attend to them. To be clear, if you've only experienced working from home during COVID-19 lockdown, you may have suffered from many of these problems without realising the benefits of flexibility.
To add spite to injury, many workplaces tried to carry on as if nothing had changed, apart from the physical location of people. Office hours were still in effect, and work now took place over video calls. If you spent eight hours on Teams or Zoom, that's not flexible working conditions. Rather, it's the worst of both worlds. The only benefit is that you avoid the commute.
Remote compared to asynchronous work #
As outlined above, remote work isn't necessarily flexible. Flexibility comes from asynchronous work processes more than physical location. The flexibility is a result of the freedom to chose when to work, more than where to work.
Based on my decades of experience working asynchronously from home, I published an article about the trade-off between latency and throughput, comparing working together in an office with working asynchronously from home. The point is that you can make both work, but the way you organise work matters. In-office work is efficient if everyone is at the office at the same time. Remote work is efficient if people can work asynchronously.
As is usually the case, there are trade-offs. The disadvantage of working together is that you must all be present simultaneously. Thus, you don't get the flexibility of choosing when to work. The benefits of working asynchronously is exactly that flexibility, but on the other hand, you lose the advantage of the efficient, high-bandwidth communication that comes from being physically in the same room as others.
Inclusion through flexibility? #
I was recently listening to an episode of the Freakonomics Radio podcast. As a side remark, someone mentioned that for women an important workplace criterion is flexibility. This, clearly, has some implications for this discussion.
There's a strong statistical tendency for women to have work-life priorities different from men. For example, Eurostat reports that women are more likely to work part-time. That may be a signifier that although women want to work, they may want to work less than men. Or perhaps with more flexible hours.
If that's true, what does it mean for software development?
If you want to include people who value flexibility highly (e.g. some women, but also me) then work should be structured to enable people to engage with it when they have the time. That might include early in the morning, late in the evening, or during the weekend.
Two workers who value flexibility may not be on the same schedule. When collaborating, they may have to do so asynchronously. Emails, work item trackers, pull requests.
Inclusive collaboration #
Most software development takes place in teams. Various team members have different skills, which is good, because a modern software system comprises more components than most people can overcome. Unless you're one of those rainbow unicorns who master modern front-end development, back-end development, DevOps, database design and administration, graphical design, security concerns, cloud computing platforms, reporting and analytics, etc. you'll need to collaborate with team members.
You can do so with short-lived Git branches, agile pull requests, and generally well-written communication. No, pull requests and asynchronous reviews don't have to be slow.
Recently, I've noticed an increased tendency among some software development thought leaders to extol the virtues of pair- and ensemble programming. These are great collaboration techniques. I've used them with great success in specific contexts. I also write about their advantages in my book Code That Fits in Your Head.
Pair- and ensemble programming are synchronous collaboration techniques. There are clear advantages to them, but it's a requirement that team members participate at the same time.
I'm sure it's fun and stimulating if you're already mostly extravert, but it doesn't strike me as particularly inclusive, time-wise.
If you can't be at the office 9-17 you can't participate. Sorry, we can't use you then.
What's that, you say? You can work some hours during the day, evenings, and sometimes weekends? But only twenty-five hours a week? Sorry, that doesn't fit our process.
A high-throughput alternative #
Pair- and ensemble programming are great collaboration techniques, but I've noticed an increased tendency to contrast them to a particular style of siloed, slow solo work with which I'm honestly not familiar. I do, however, consider that a false dichotomy.
The alternative to ensemble programming doesn't have to be slow, waterfall-like, feature-branch-based solo work heavy on misunderstandings, integration problems, and rework. It can be asynchronous, pull-based work. Lean.
I've lived that dream. I know that it can work. Is it easy? No. Does it require discipline? Yes. But it's possible, and it's flexible. It enables people to work when they have the time.
Conclusion #
There are people who would like to work, just not 9-17. Perhaps they can't (for all sorts of socio-economic reasons), or perhaps that just doesn't align with their life choices. Perhaps they're just not in your time zone.
Do you want to include these people, or exclude them?
Epistemology of interaction testing
How do we know that components interact correctly?
Most software systems are composed as a graph of components. To be clear, I use the word component loosely to mean a collection of functionality - it may be an object, a module, a function, a data type, or perhaps something else I haven't thought of. Some components deal with the bigger picture and will typically coordinate other components that perform more specific tasks. If we think of a component graph as a tree, then some components are leaves.
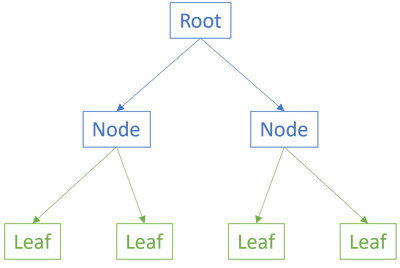
Leaf components, being self-contained and without dependencies, are typically the easiest to test. Most test-driven development (TDD) katas focus on these kinds of components: Tennis, bowling, diamond, Roman numerals, gossiping bus drivers, and so on. Even the legacy security manager kata is simple and quite self-contained. There's nothing wrong with that, and there's good reason to keep such exercises simple. After all, you want to be able to complete a kata in a few hours. You can hardly do that if the exercise is to develop an entire web site with user interface, persistent data storage, security, data validation, business logic, third-party integration, emails, instrumentation and logging, and so on.
This means that even if you get good at TDD against 'leaf' functionality, you may be struggling when it comes to higher-level components. How does one unit test code that has dependencies?
Interaction-based testing #
A common solution is to invert the dependencies. You can, for example, use Dependency Injection to inject Test Doubles into the System Under Test (SUT). This enables you to control the behaviour of the dependencies and to verify that the SUT behaves as expected. Not only that, but you can also verify that the SUT interacts with the dependencies as expected. This is called interaction-based testing. It is, perhaps, the most common form of unit testing in the industry, and exemplary explained in Growing Object-Oriented Software, Guided by Tests.
The kinds of Test Doubles most useful with interaction-based testing are Stubs and Mocks. They are, however, problematic because they break encapsulation. And encapsulation, to be clear, is also a concern in functional programming.
I have already described how to move from interaction-based to state-based testing, and why functional programming is intrinsically more testable.
How to test composition of pure functions? #
When you adopt functional programming (FP) you'll sooner or later need to compose or orchestrate pure functions. How do you test that the composition of pure functions is correct? That's what you can test with a Mock or Spy.
You've developed component A, perhaps as a higher-order function, that depends on another component B. You want to test that A correctly interacts with B, but if interaction-based testing is no longer 'allowed' (because it breaks encapsulation), then what do you do?
For a long time, I pondered that question myself, while I was busy enjoying FP making most things easier. It took me some time to understand that the answer, as is often the case, is mu. I'll get back to that later.
I'm not the only one struggling with this question. Sergei Rogovtcev writes and asks what I interpret as the same question:
"I do have a component A, which is, frankly, some controller doing some checks and processing around a fairly complex state. This process can have several outcomes, let's call them Success, Fail, and Missing (the actual states are not important, but I'd like to have more than two). Then we have a component B, which is responsible for the rendering of the result. Of course, three different states lead to three different renderings, but the renderings are also influenced by state (let's say we have browser, mobile and native clients, and we need to provide different renderings). Originally the components are objects, B having three separate methods, but I can express them as pure functions, at least for the purpose of this discussion - A, and then BSuccess, BFail and BMissing. I can easily test each part of B in isolation; the problem comes when I need to test A, which calls different parts of B. If I use mocks, the solution is simple - I inject a mock of B to A, and then verify that A calls appropriate parts according to the process result. This requires knowing the innards of A, but otherwise it is a well-known and well-understood approach. But if I want to avoid mocks, what do I do? I cannot test A without relying on some code path in B, and this to me means that I'm losing the benefits of unit testing and entering the realm of integration testing."
In his email Sergei Rogovtcev has explicitly given me permission to quote him and engage with this question. As I've outlined, I've grappled with that question myself, so I find the question worthwhile. I can't, however, work with it without questioning the premise. This is not an attack on Sergei Rogovtcev; after all, I had that question myself, so any critique I make is directed as much at my former self as at him.
Axiomatic versus scientific knowledge #
It may be helpful to elevate the discussion. How do we know that software (or a subsystem thereof) works? You could say that one answer to that is: Passing tests. If all tests are passing, we may have high confidence that the system works.
In the parlance of Sergei Rogovtcev, we can easily unit test component B because it's composed from pure functions.
How do we unit test component A, though? With Mocks and Stubs, you can prove that the interaction works as intended. The keyword here is prove. If you assume that component B works correctly, 'all' you have to do is to demonstrate that component A correctly interacts with component B. I used to do that all the time and called it data-flow verification or structural inspection. The idea was that if you could demonstrate that component A correctly interacts with any LSP-compliant implementation of component B, and then also demonstrate that in reality (when composed in the Composition Root) component A is composed with a component B that has also been demonstrated to work correctly, then the (sub-)system works correctly.
This is almost like a mathematical proof. First prove lemma B, then prove theorem A using lemma B. Finally, state corollary C: b is a special case handled by lemma B, so therefore a is covered by theorem A. Q.E.D.
It's a logical and deductive approach to the problem of verifying the composition of the whole from verified parts. It's almost mathematical in the sense that it tries to erect an axiomatic system.
It's also fundamentally flawed.
I didn't understand that a decade ago, and in practice, the method worked well enough - apart from all the problems stemming from poor encapsulation. The problem with that approach is that an axiomatic system is only as strong as its axioms. What are the axioms in this system? The axioms, or premises, are that each of the components (A and B) are already correct. Based on these premises, this testing approach then proves that the composition is also correct.
How do we know that the components work correctly?
In this context, the answer is that they pass all tests. This, however, doesn't constitute any kind of proof. Rather, this is experimental knowledge, more reminiscent of science than of mathematics.
Why are we trying to prove, then, that composition works correctly? Why not just test it?
This observation cuts to the heart of the epistemology of testing. How do we know that software works? Typically not by proving it correct, but by subjecting it to experiments. As I've also outlined in Code That Fits in Your Head, we can regard automated tests as scientific experiments that we repeat over and over.
Integration testing #
To outline the argument so far: While you can use Mocks and Spies to verify that a component correctly interacts with another component, this may be overkill. You're essentially trying to prove a conjecture based on doubtful evidence.
Does it really matter that two components interact correctly? Aren't the components implementation details? Do users care?
Users and other stakeholders care about the behaviour of the software system. Why not test that?
This is, unfortunately, easier said than done. Sergei Rogovtcev strongly implies that he isn't keen on integration testing. While he doesn't explicitly state why, there are good reasons to be wary of integration testing. As J.B. Rainsberger eloquently explained, a major problem with integration testing is the combinatorial explosion of test cases. If you ought to write 53,000 test cases to cover all combinations of pathways through integrated components, which test cases do you write? Surely not all 53,000.
J.B. Rainsberger's argument is that if you're going to write no more than a dozen unit tests, you're unlikely to cover enough test cases to be confident that the system works.
What if, however, you could write hundreds or thousands of test cases?
Property-based testing #
You may recall that the premise of this article is functional programming (FP), where property-based testing is a common testing technique. While you can, to a degree, also use this technique in object-oriented programming (OOP), it's often difficult because of side effects and non-deterministic behaviour.
When you write a property-based test, you write a single piece of code that evaluates a property of the SUT. The property looks like a parametrised unit test; the difference is that the input is generated randomly, but in a fashion you can control. This enables you to write hundreds or thousands of test cases without having to write them explicitly.
Thus, epistemologically, you can use property-based testing with integrated components to produce confidence that the (sub-)system works. In practice, I find that the confidence I get from this technique is at least as high as the one I used to get from unit testing with Stubs and Spies.
Examples #
All of this is abstract and theoretical, I realise. An example would be handy right about now. Such examples, however, are complex enough to warrant their own articles:
- Confidence from Facade Tests
- An abstract example of refactoring from interaction-based to property-based testing
- A restaurant example of refactoring from example-based to property-based testing
- Refactoring pure function composition without breaking existing tests
- When is an implementation detail an implementation detail?
Sergei Rogovtcev was kind enough to furnish a rather abstract, but minimal and self-contained, example. I'll go through that first, and then follow up with a more realistic example.
Conclusion #
How do you know that a software system works correctly? Ultimately, if it behaves in the way it's supposed to, it works correctly. Testing an entire system from the outside, however, is rarely viable in itself. The number of possible test cases is just too large.
You can partially address that problem by decomposing the system into components. You can then test the components individually, and verify that they interact correctly. This last part is the topic of this article. A common way to to address this problem is to use Mocks and Spies to prove interactions correct. It does solve the problem of correctness quite neatly, but has the undesirable side effect of making the tests brittle.
An alternative is to use property-based testing to verify that the components integrate correctly. Rather than something that looks like a proof, this is a question of numbers. Throw enough random test cases at the system, and you'll be confident that it works. How many? Enough.
Next: Confidence from Facade Tests.
Comments
First of all, let me thank you for taking time and effort to discuss this.
There's a minor point about integration testing:
[SR] strongly implies that he isn't keen on integration testing. While he doesn't explicitly state why...
The situation is somewhat more complicated: in fact, I tend to have at least a few integration tests for a feature I'm involved with, starting the coverage from the happy paths (the minimum requirement being to verify that we've wired correctly as many components as can be verified), and then, if possible, extending to error paths, edge cases and so on. Even the code from my email originally had integration tests covering all the outcomes for a single rendering (browser). The problem that I've faced then, and which prompted my question, was exactly the one that you quote from J.B. Rainsberger: combinatorial explosion. As soon as I decided to cover a second rendering (mobile), I saw that I needed to replicate the setups for outcomes (success/fail/missing), but modify the asserts for their rendering. And then again the same for the native client. Unit tests, even with their ungainly break in encapsulation, gave the simple appeal of writing less code...
Hopefully, this seem to be the very same premise that you explore towards the end of your post, leading to the property-based testing - which I was trying to incorporate into my toolset for quite some time, but was always somewhat baffled at how it should work and integrate into object-oriented (and C#-based) code. So I'm very much looking forward for your next installment in this series.
And again, thank you for exploring these matters.
Sergei, thank you for writing. I hope that this small series of articles will be able to at least give you some ideas. I am, however, concerned that I may miss the mark.
When discussing problems like this, there's always a risk that the examples we look at are too simple; that they don't adequately represent the real world. For instance, we may look at the example code in the next few articles and calculate how well we've covered all combinations.
Perhaps we may find that the combinatorial 'explosion' is only in the ten-thousands, which is within reasonable reach of well-written properties.
Then, when we come back to our 'real' problems, the combinatorial explosion may be orders of magnitudes larger. You can easily ask a property-based framework to run a property millions of time, but it'll take time. Perhaps this makes the tests so slow that it's not a practical solution.
All that said, I think that not all is lost. Part of the solution, however, may be found elsewhere.
The more I learn about functional programming (FP), the more I'm amazed at the alternative mindset it offers. Solutions that look in one way in object-oriented programming (OOP) may look completely different in FP. You've probably noticed this yourself. Often, you have to turn a problem on its head to see it 'the FP way'.
The following is something that I've not yet thought through rigorously, so perhaps there are flaws in my thinking. I offer it for peer review here.
OOP composition tends to be 'deep'. If we think of object composition as a directed (acyclic, hopefully!) graph, typical OOP composition might resemble a graph where each node has only few children, but the distance from the root to each leaf is great. Since, every time you compose two objects, you have to multiply the number of pathways, this gives you this combinatorial explosion we've discussed. The deeper the graph, the worse it is.
In FP I typically find myself composing functions in a more shallow fashion. Instead of having functions that call other functions that call other functions, etc. I tend to have functions that return values that I then pass to other functions, and so on. This produces a shallower and wider composition graph. Doesn't it also reduce the combinations that we need to consider for testing?
I haven't subjected this idea to a more formal analysis yet, so this may be wrong. If I'm right, though, this could mean that property-based testing is still a viable solution to the problem.
Identifying useful properties is another problem that you also bring up, particularly in the context of OOP. So far, property-based testing is more prevalent in FP, and perhaps there's a reason for that.
It seems to me that there's a connection between property-based testing and encapsulation. Essentially, a property is an executable description of some invariant, or pre- or post-condition. Most real-world object-oriented code I've seen, however, isn't encapsulated. If you have poor encapsulation, it's no wonder that it's hard to identify useful properties.
Even so, Identifying good properties is a skill that you have to learn. It's fairly easy to construct properties that, in a sense, 'reproduce the implementation'. The challenge is to avoid that, and that's not always easy. As an example, it took me years before I found a good way to express properties of FizzBuzz without repeating the implementation.
This produces a shallower and wider composition graph. Doesn't it also reduce the combinations that we need to consider for testing?
Intuitively I'd say that it shouldn't (reduce), because in the end the number of combinations that we consider for testing is the number states our SUT can be in, which is defined as a combination of all its inputs. But I may, of course, miss something important here.
My own opinion on this, coming from a short-ish brush with FP, is that FP, or, more precisely, more expressive type systems, reduce the number of combinations by reducing the number of possible inputs by the virtue of more expressive types. My favorite example is that even less expressive type system, one with simple int and string instead of all-encompassing var/object, allows us to get rid off all the tests where we pass "foo" to a function that only works on numbers. Explicit nullability gets rid of all the null-related test-cases (and we get an indication where we lack such cases for null-accepting functions). This can be continued by adding more and more cases until we arrive at the (in)famous "if it compiles, is works".
I don't remember whether I've included this guard case in my original email, but I definitely remember thinking of mentioning that I'm confined to a less-expressive type system of C#. Even comparing to F# (as I remember it from my side studies), I can see how some tests can be made redundant by, for example, introducing a sum type and then relying on compiler to check for exhaustive match. Sometimes I wonder what would a more expressive type system do to these problems...
Sergei, thank you for writing. A more expressive type system certainly does reduce the amount of testing required. While I prefer F#, the good news is that most of what F# can do, C# can do, too. Everything is just more verbose in C#. The main stumbling block that people usually complain about is the lack of sum types, but you can use Visitors as sum types. You get the same benefits as with F# discriminated unions, except with much more ceremony.
Contravariant functors as invariant functors
Another most likely useless set of invariant functors that nonetheless exist.
This article is part of a series of articles about invariant functors. An invariant functor is a functor that is neither covariant nor contravariant. See the series introduction for more details.
It turns out that all contravariant functors are also invariant functors.
Is this useful? Let me, like in the previous article, be honest and say that if it is, I'm not aware of it. Thus, if you're interested in practical applications, you can stop reading here. This article contains nothing of practical use - as far as I can tell.
Because it's there #
Why describe something of no practical use?
Why do some people climb Mount Everest? Because it's there, or for other irrational reasons. Which is fine. I've no personal goals that involve climbing mountains, but I happily engage in other irrational and subjective activities.
One of them, apparently, is to write articles of software constructs of no practical use, because it's there.
All contravariant functors are also invariant functors, even if that's of no practical use. That's just the way it is. This article explains how, and shows a few (useless) examples.
I'll start with a few Haskell examples and then move on to showing the equivalent examples in C#. If you're unfamiliar with Haskell, you can skip that section.
Haskell package #
For Haskell you can find an existing definition and implementations in the invariant package. It already makes most 'common' contravariant functors Invariant instances, including Predicate, Comparison, and Equivalence. Here's an example of using invmap with a predicate.
First, we need a predicate. Consider a function that evaluates whether a number is divisible by three:
isDivisbleBy3 :: Integral a => a -> Bool isDivisbleBy3 = (0 ==) . (`mod` 3)
While this is already conceptually a contravariant functor, in order to make it an Invariant instance, we have to enclose it in the Predicate wrapper:
ghci> :t Predicate isDivisbleBy3 Predicate isDivisbleBy3 :: Integral a => Predicate a
This is a predicate of some kind of integer. What if we wanted to know if a given duration represented a number of picoseconds divisible by three? Silly example, I know, but in order to demonstrate invariant mapping, we need types that are isomorphic, and NominalDiffTime is isomorphic to a number of picoseconds via its Enum instance.
p :: Enum a => Predicate a p = invmap toEnum fromEnum $ Predicate isDivisbleBy3
In other words, it's possible to map the Integral predicate to an Enum predicate, and since NominalDiffTime is an Enum instance, you can now evaluate various durations:
ghci> (getPredicate p) $ secondsToNominalDiffTime 60 True ghci> (getPredicate p) $ secondsToNominalDiffTime 61 False
This is, as I've already announced, hardly useful, but it's still possible. Unless you have an API that requires an Invariant instance, it's also redundant, because you could just have used contramap with the predicate:
ghci> (getPredicate $ contramap fromEnum $ Predicate isDivisbleBy3) $ secondsToNominalDiffTime 60 True ghci> (getPredicate $ contramap fromEnum $ Predicate isDivisbleBy3) $ secondsToNominalDiffTime 61 False
When mapping a contravariant functor, only the contravariant mapping argument is required. The Invariant instances for Contravariant simply ignores the covariant mapping argument.
Specification as an invariant functor in C# #
My earlier article The Specification contravariant functor takes a more object-oriented view on predicates by examining the Specification pattern.
As outlined in the introduction, while it's possible to add a method called InvMap, it'd be more idiomatic to add a non-standard Select method:
public static ISpecification<T1> Select<T, T1>( this ISpecification<T> source, Func<T, T1> tToT1, Func<T1, T> t1ToT) { return source.ContraMap(t1ToT); }
This implementation ignores tToT1 and delegates to the existing ContraMap method.
Here's a unit test that demonstrates an example equivalent to the above Haskell example:
[Theory] [InlineData(60, true)] [InlineData(61, false)] public void InvariantMappingExample(long seconds, bool expected) { ISpecification<long> spec = new IsDivisibleBy3Specification(); ISpecification<TimeSpan> mappedSpec = spec.Select(ticks => new TimeSpan(ticks), ts => ts.Ticks); Assert.Equal( expected, mappedSpec.IsSatisfiedBy(TimeSpan.FromSeconds(seconds))); }
Again, while this is hardly useful, it's possible.
Conclusion #
All contravariant functors are invariant functors. You simply use the 'normal' contravariant mapping function (contramap in Haskell). This enables you to add an invariant mapping (invmap) that only uses the contravariant argument (b -> a) and ignores the covariant argument (a -> b).
Invariant functors are, however, not particularly useful, so neither is this result. Still, it's there, so deserves a mention. Enough of that, though.
Next: Monads.
Built-in alternatives to applicative assertions
Why make things so complicated?
Several readers reacted to my small article series on applicative assertions, pointing out that error-collecting assertions are already supported in more than one unit-testing framework.
"In the Java world this seems similar to the result gained by Soft Assertions in AssertJ. https://assertj.github.io/doc/#assertj-c... if you’re after a target for functionality (without the adventures through monad land)"
While I'm not familiar with the details of Java unit-testing frameworks, the situation is similar in .NET, it turns out.
"Did you know there is Assert.Multiple in NUnit and now also in xUnit .Net? It seems to have quite an overlap with what you're doing here.
"For a quick overview, I found this blogpost helpful: https://www.thomasbogholm.net/2021/11/25/xunit-2-4-2-pre-multiple-asserts-in-one-test/"
I'm not surprised to learn that something like this exists, but let's take a quick look.
NUnit Assert.Multiple #
Let's begin with NUnit, as this seems to be the first .NET unit-testing framework to support error-collecting assertions. As a beginning, the documentation example works as it's supposed to:
[Test] public void ComplexNumberTest() { ComplexNumber result = SomeCalculation(); Assert.Multiple(() => { Assert.AreEqual(5.2, result.RealPart, "Real part"); Assert.AreEqual(3.9, result.ImaginaryPart, "Imaginary part"); }); }
When you run the test, it fails (as expected) with this error message:
Message: Multiple failures or warnings in test: 1) Real part Expected: 5.2000000000000002d But was: 5.0999999999999996d 2) Imaginary part Expected: 3.8999999999999999d But was: 4.0d
That seems to work well enough, but how does it actually work? I'm not interested in reading the NUnit source code - after all, the concept of encapsulation is that one should be able to make use of the capabilities of an object without knowing all implementation details. Instead, I'll guess: Perhaps Assert.Multiple executes the code block in a try/catch block and collects the various exceptions thrown by the nested assertions.
Does it catch all exception types, or only a subset?
Let's try with the kind of composed assertion that I previously investigated:
[Test] public void HttpExample() { var deleteResp = new HttpResponseMessage(HttpStatusCode.BadRequest); var getResp = new HttpResponseMessage(HttpStatusCode.OK); Assert.Multiple(() => { deleteResp.EnsureSuccessStatusCode(); Assert.That(getResp.StatusCode, Is.EqualTo(HttpStatusCode.NotFound)); }); }
This test fails (again, as expected). What's the error message?
Message: System.Net.Http.HttpRequestException :↩ Response status code does not indicate success: 400 (Bad Request).
(I've wrapped the result over multiple lines for readability. The ↩ symbol indicates where I've wrapped the text. I'll do that again later in this article.)
Notice that I'm using EnsureSuccessStatusCode as an assertion. This seems to spoil the behaviour of Assert.Multiple. It only reports the first status code error, but not the second one.
I admit that I don't fully understand what's going on here. In fact, I have taken a cursory glance at the relevant NUnit source code without being enlightened.
One hypothesis might be that NUnit assertions throw special Exception sub-types that Assert.Multiple catch. In order to test that, I wrote a few more tests in F# with Unquote, assuming that, since Unquote hardly throws NUnit exceptions, the behaviour might be similar to above.
[<Test>] let Test4 () = let x = 1 let y = 2 let z = 3 Assert.Multiple (fun () -> x =! y y =! z)
The =! operator is an Unquote operator that I usually read as must equal. How does that error message look?
Message: Multiple failures or warnings in test: 1) 1 = 2 false 2) 2 = 3 false
Somehow, Assert.Multiple understands Unquote error messages, but not HttpRequestException. As I wrote, I don't fully understand why it behaves this way. To a degree, I'm intellectually curious enough that I'd like to know. On the other hand, from a maintainability perspective, as a user of NUnit, I shouldn't have to understand such details.
xUnit.net Assert.Multiple #
How fares the xUnit.net port of Assert.Multiple?
[Fact] public void HttpExample() { var deleteResp = new HttpResponseMessage(HttpStatusCode.BadRequest); var getResp = new HttpResponseMessage(HttpStatusCode.OK); Assert.Multiple( () => deleteResp.EnsureSuccessStatusCode(), () => Assert.Equal(HttpStatusCode.NotFound, getResp.StatusCode)); }
The API is, you'll notice, not quite identical. Where the NUnit Assert.Multiple method takes a single delegate as input, the xUnit.net method takes an array of actions. The difference is not only at the level of API; the behaviour is different, too:
Message: Multiple failures were encountered: ---- System.Net.Http.HttpRequestException :↩ Response status code does not indicate success: 400 (Bad Request). ---- Assert.Equal() Failure Expected: NotFound Actual: OK
This error message reports both problems, as we'd like it to do.
I also tried writing equivalent tests in F#, with and without Unquote, and they behave consistently with this result.
If I had to use something like Assert.Multiple, I'd trust the xUnit.net variant more than NUnit's implementation.
Assertion scopes #
Apparently, Fluent Assertions offers yet another alternative.
"Hey @ploeh, been reading your applicative assertion series. I recently discovered Assertion Scopes, so I'm wondering what is your take on them since it seems to me they are solving this problem in C# already. https://fluentassertions.com/introduction#assertion-scopes"
The linked documentation contains this example:
[Fact] public void DocExample() { using (new AssertionScope()) { 5.Should().Be(10); "Actual".Should().Be("Expected"); } }
It fails in the expected manner:
Message: Expected value to be 10, but found 5 (difference of -5). Expected string to be "Expected" with a length of 8, but "Actual" has a length of 6,↩ differs near "Act" (index 0).
How does it fare when subjected to the EnsureSuccessStatusCode test?
[Fact] public void HttpExample() { var deleteResp = new HttpResponseMessage(HttpStatusCode.BadRequest); var getResp = new HttpResponseMessage(HttpStatusCode.OK); using (new AssertionScope()) { deleteResp.EnsureSuccessStatusCode(); getResp.StatusCode.Should().Be(HttpStatusCode.NotFound); } }
That test produces this error output:
Message: System.Net.Http.HttpRequestException :↩ Response status code does not indicate success: 400 (Bad Request).
Again, EnsureSuccessStatusCode prevents further assertions from being evaluated. I can't say that I'm that surprised.
Implicit or explicit #
You might protest that using EnsureSuccessStatusCode and treating the resulting HttpRequestException as an assertion is unfair and unrealistic. Possibly. As usual, such considerations are subject to a multitude of considerations, and there's no one-size-fits-all answer.
My intent with this article isn't to attack or belittle the APIs I've examined. Rather, I wanted to explore their boundaries by stress-testing them. That's one way to gain a better understanding. Being aware of an API's limitations and quirks can prevent subtle bugs.
Even if you'd never use EnsureSuccessStatusCode as an assertion, perhaps you or a colleague might inadvertently do something to the same effect.
I'm not surprised that both NUnit's Assert.Multiple and Fluent Assertions' AssertionScope behaves in a less consistent manner than xUnit.net's Assert.Multiple. The clue is in the API.
The xUnit.net API looks like this:
public static void Multiple(params Action[] checks)
Notice that each assertion is explicitly a separate action. This enables the implementation to isolate it and treat it independently of other actions.
Neither the NUnit nor the Fluent Assertions API is that explicit. Instead, you can write arbitrary code inside the 'scope' of multiple assertions. For AssertionScope, the notion of a 'scope' is plain to see. For the NUnit API it's more implicit, but the scope is effectively the extent of the method:
public static void Multiple(TestDelegate testDelegate)
That testDelegate can have as many (nested, even) assertions as you'd like, so the Multiple implementation needs to somehow demarcate when it begins and when it ends.
The testDelegate can be implemented in a different file, or even in a different library, and it has no way to communicate or coordinate with its surrounding scope. This reminds me of an Ambient Context, an idiom that Steven van Deursen convinced me was an anti-pattern. The surrounding context changes the behaviour of the code block it surrounds, and it's quite implicit.
Explicit is better than implicit.
The xUnit.net API, at least, looks a bit saner. Still, this kind of API is quirky enough that it reminds me of Greenspun's tenth rule; that these APIs are ad-hoc, informally-specified, bug-ridden, slow implementations of half of applicative functors.
Conclusion #
Not surprisingly, popular unit-testing and assertion libraries come with facilities to compose assertions. Also, not surprisingly, these APIs are crude and require you to learn their implementation details.
Would I use them if I had to? I probably would. As Rich Hickey put it, they're already at hand. That makes them easy, but not necessarily simple. APIs that compel you to learn their internal implementation details aren't simple.
Universal abstractions, on the other hand, you only have to learn one time. Once you understand what an applicative functor is, you know what to expect from it, and which capabilities it has.
In languages with good support for applicative functors, I would favour an assertion API based on that abstraction, if given a choice. At the moment, though, that's not much of an option. Even HUnit assertions are based on side effects.
Comments
Just a reminder: in .NET, method's execution cannot be resumed after an exception is thrown, there is just simply no way to do this, at all. Which means that NUnit's Assert.Multiple absolutely cannot work the way you guess it probably does, by running the delegate and resuming its execution after it throws an exception until the delegate returns.
How could it work then? Well, considering that documentation to almost every Assert's method has "Returns without throwing an exception when inside a multiple assert block" line in it, I would assume that Assert.Multiple sets a global flag which makes actual assertions to store the failures in some global hidden context instead on throwing them, then runs the delegate and after it finishes or throws, collects and clears all those failures from the context and resets the global flag.
Cursory inspection of NUnit's source code supports this idea, except that apparently it's not just a boolean flag but a "depth" counter; and assertions report the failures just the way I've speculated. I personally hate such side-channels but you have to admit, they allow for some nifty, seemingly impossible magical tricks (a.k.a. "spooky action at the distance").
Also, why do you assume that Unquote would not throw NUnit's assertions? It literally has "Unquote integrates configuration-free with all exception-based unit testing frameworks including xUnit.net, NUnit, MbUnit, Fuchu, and MSTest" in its README, and indeed, if you look at its source code, you'll see that at runtime it tries to locate any testing framework it's aware of and use its assertions. More funny party tricks, this time with reflection!
I understand that after working in more pure/functional programming environments one does start to slowly forget about those terrible things, but: those horrorterrors still exist, and people keep making more of them. Now, if you can, have a good night :)
Joker_vD, thank you for explaining those details. I admit that I hadn't thought too deeply about implementation details, for the reasons I briefly mentioned in the post.
"I understand that after working in more pure/functional programming environments one does start to slowly forget about those terrible things"
Yes, that summarises my current thinking well, I'm afraid.
NUnit has Assert.DoesNotThrow and Fluent Assertions has .Should().NotThrow(). I did not check Fluent Assertions, but NUnit does gather failures of Assert.DoesNotThrow inside Assert.Multiple into a multi-error report. One might argue that asserting that a delegate should not throw is another application of the "explicit is better than implicit" philosophy. Here's what Fluent Assertions has to say on that matter:
"We know that a unit test will fail anyhow if an exception was thrown, but this syntax returns a clearer description of the exception that was thrown and fits better to the AAA syntax."
As a side note, you might also want to take a look on NUnits Assert.That syntax. It allows to construct complex conditions tested against a single actual value:
int actual = 3; Assert.That (actual, Is.GreaterThan (0).And.LessThanOrEqualTo (2).And.Matches (Has.Property ("P").EqualTo ("a")));
A failure is then reported like this:
Expected: greater than 0 and less than or equal to 2 and property P equal to "a" But was: 3
Max, thank you for writing. I have to admit that I never understood the point of NUnit's constraint model, but your example clearly illustrates how it may be useful. It enables you to compose assertions.
It's interesting to try to understand the underlying reason for that. I took a cursory glance at that IResolveConstraint API, and as far as I can tell, it may form a monoid (I'm not entirely sure about the ConstraintStatus enum, but even so, it may be 'close enough' to be composable).
I can see how that may be useful when making assertions against complex objects (i.e. object composed from other objects).
In xUnit.net you'd typically address that problem with custom IEqualityComparers. This is more verbose, but also strikes me as more reusable. One disadvantage of that approach, however, is that when tests fail, the assertion message is typically useless.
This is the reason I favour Unquote: Instead of inventing a Boolean algebra(?) from scratch, it uses the existing language and still gives you good error messages. Alas, that only works in F#.
In general, though, I'm inclined to think that all of these APIs address symptoms rather than solve real problems. Granted, they're useful whenever you need to make assertions against values that you don't control, but for your own APIs, a simpler solution is to model values as immutable data with structural equality.
Another question is whether aiming for clear assertion messages is optimising for the right concern. At least with TDD, I don't think that it is.
Agilean
There are other agile methodologies than scrum.
More than twenty years after the Agile Manifesto it looks as though there's only one kind of agile process left: Scrum.
I recently held a workshop and as a side remark I mentioned that I don't consider scrum the best development process. This surprised some attendees, who politely inquired about my reasoning.
My experience with scrum #
The first nine years I worked as a professional programmer, the companies I worked in used various waterfall processes. When I joined the Microsoft Dynamics Mobile team in 2008 they were already using scrum. That was my first exposure to it, and I liked it. Looking back on it today, we weren't particular dogmatic about the process, being more interested in getting things done.
One telling fact is that we took turns being Scrum Master. Every sprint we'd rotate that role.
We did test-driven development, and had two-week sprints. This being a Microsoft development organisation, we had a dedicated build master, tech writers, specialised testers, and security reviews.
I liked it. It's easily one of the most professional software organisations I've worked in. I think it was a good place to work for many reasons. Scrum may have been a contributing factor, but hardly the only reason.
I have no issues with scrum as we practised it then. I recall later attending a presentation by Mike Cohn where he outlined four quadrants of team maturity. You'd start with scrum, but use retrospectives to evaluate what worked and what didn't. Then you'd adjust. A mature, self-organising team would arrive at its own process, perhaps initiated with scrum, but now having little resemblance with it.
I like scrum when viewed like that. When it becomes rigid and empty ceremony, I don't. If all you do is daily stand-ups, sprints, and backlogs, you may be doing scrum, but probably not agile.
Continuous deployment #
After Microsoft I joined a startup so small that formal process was unnecessary. Around that time I also became interested in lean software development. In the beginning, I learned a lot from Martin Jul who seemed to use the now-defunct Ative blog as a public notepad as he was reading works of Deming. I suppose, if you want a more canonical introduction to the topic, that you might start with one of the Poppendiecks' books, but since I've only read Implementing Lean Software Development, that's the only one I can recommend.
Around 2014 I returned to a regular customer. The team had, in my absence, been busy implementing continuous deployment. Instead of artificial periods like 'sprints' we had a kanban board to keep track of our work. We used a variation of feature flags and marked features as done when they were complete and in production.
Why wait until next Friday if the feature is done, done on a Wednesday? Why wait until the next Monday to identify what to work on next, if you're ready to take on new work on a Thursday? Why not move towards one-piece flow?
An effective self-organising team typically already knows what it's doing. Much process is introduced in order to give external stakeholders visibility into what a team is doing.
I found, in that organisation, that continuous deployment eliminated most of that need. At one time I asked a stakeholder what he thought of the feature I'd deployed a week before - a feature that he had requested. He replied that he hadn't had time to look at it yet.
The usual inquires about status (Is it done yet? When is it done?) were gone. The team moved faster than the stakeholders could keep up. That also gave us enough slack to keep the code base in good order. We also used test-driven development throughout (TDD).
TDD with continuous deployment and a kanban board strikes me as congenial with the ideas of lean software development, but that's not all.
Stop-the-line issues #
An andon cord is a central concept in lean manufactoring. If a worker (or anyone, really) discovers a problem during production, he or she pulls the andon cord and stops the production line. Then everyone investigates and determines what to do about the problem. Errors are not allowed to accumulate.
I think that I've internalised this notion to such a degree that I only recently connected it to lean software development.
In Code That Fits in Your Head, I recommend turning compiler warnings into errors at the beginning of a code base. Don't allow warnings to pile up. Do the same with static code analysis and linters.
When discussing software engineering with developers, I'm beginning to realise that this runs even deeper.
- Turn warnings into errors. Don't allow warnings to accumulate.
- The correct number of unhandled exceptions in production is zero. If you observe an unhandled exception in your production logs, fix it. Don't let them accumulate.
- The correct number of known bugs is zero. Don't let bugs accumulate.
If you're used to working on a code base with hundreds of known bugs, and frequent exceptions in production, this may sound unrealistic. If you deal with issues as soon as they arise, however, this is not only possible - it's faster.
In lean software development, bugs are stop-the-line issues. When something unexpected happens, you stop what you're doing and make fixing the problem the top priority. You build quality in.
This has been my modus operandi for years, but I only recently connected the dots to realise that this is a typical lean practice. I may have picked it up from there. Or perhaps it's just common sense.
Conclusion #
When Agile was new and exciting, there were extreme programming and scrum, and possibly some lesser known techniques. Lean was around the corner, but didn't come to my attention, at least, until around 2010. Then it seems to have faded away again.
Today, agile looks synonymous with scrum, but I find lean software development more efficient. Why divide work into artificial time periods when you can release continuously? Why plan bug fixing when it's more efficient to stop the line and deal with the problem as it arises?
That may sound counter-intuitive, but it works because it prevents technical debt from accumulating.
Lean software development is, in my experience, a better agile methodology than scrum.
In the long run
Software design decisions should be time-aware.
A common criticism of modern capitalism is that maximising shareholder value leads to various detrimental outcomes, both societal, but possibly also for the maximising organisation itself. One major problem is when company leadership is incentivised to optimise stock market price for the next quarter, or other short terms. When considering only the short term, decision makers may (rationally) decide to sacrifice long-term benefits for short-term gains.
We often see similar behaviour in democracies. Politicians tend to optimise within a time frame that coincides with the election period. Getting re-elected is more important than good policy in the next period.
These observations are crude generalisations. Some democratic politicians and CEOs take longer views. Inherent in the context, however, is an incentive to short-term thinking.
This, it strikes me, is frequently the case in software development.
Particularly in the context of scrum there's a focus on delivering at the end of every sprint. I've observed developers and other stakeholders together engage in short-term thinking in order to meet those arbitrary and fictitious deadlines.
Even when deadlines are more remote than two weeks, project members rarely think beyond some perceived end date. As I describe in Code That Fits in Your Head, a project is rarely is good way to organise software development work. Projects end. Successful software doesn't.
Regardless of the specific circumstances, a too myopic focus on near-term goals gives you an incentive to cut corners. To not care about code quality.
...we're all dead #
As Keynes once quipped:
"In the long run we are all dead."
Clearly, while you can be too short-sighted, you can also take too long a view. Sometimes deadlines matter, and software not used makes no-one happy.
Working software remains the ultimate test of value, but as I've tried to express many times before, this does not imply that anything else is worthless.
You can't measure code quality. Code quality isn't software quality. Low code quality slows you down, and that, eventually, costs you money, blood, sweat, and tears.
This is, however, not difficult to predict. All it takes is a slightly wider time horizon. Consider the impact of your decisions past the next deadline.
Conclusion #
Don't be too short-sighted, but don't forget the immediate value of what you do. Your decisions matter. The impact is not always immediate. Consider what consequences short-term optimisations may have in a longer perspective.
The IO monad
The IO container forms a monad. An article for object-oriented programmers.
This article is an instalment in an article series about monads. A previous article described the IO functor. As is the case with many (but not all) functors, this one also forms a monad.
SelectMany #
A monad must define either a bind or join function. In C#, monadic bind is called SelectMany. In a recent article, I gave an example of what IO might look like in C#. Notice that it already comes with a SelectMany function:
public IO<TResult> SelectMany<TResult>(Func<T, IO<TResult>> selector)
Unlike other monads, the IO implementation is considered a black box, but if you're interested in a prototypical implementation, I already posted a sketch in 2020.
Query syntax #
I have also, already, demonstrated syntactic sugar for IO. In that article, however, I used an implementation of the required SelectMany overload that is more explicit than it has to be. The monad introduction makes the prediction that you can always implement that overload in the same way, and yet here I didn't.
That's an oversight on my part. You can implement it like this instead:
public static IO<TResult> SelectMany<T, U, TResult>( this IO<T> source, Func<T, IO<U>> k, Func<T, U, TResult> s) { return source.SelectMany(x => k(x).Select(y => s(x, y))); }
Indeed, the conjecture from the introduction still holds.
Join #
In the introduction you learned that if you have a Flatten or Join function, you can implement SelectMany, and the other way around. Since we've already defined SelectMany for IO<T>, we can use that to implement Join. In this article I use the name Join rather than Flatten. This is an arbitrary choice that doesn't impact behaviour. Perhaps you find it confusing that I'm inconsistent, but I do it in order to demonstrate that the behaviour is the same even if the name is different.
The concept of a monad is universal, but the names used to describe its components differ from language to language. What C# calls SelectMany, Scala calls flatMap, and what Haskell calls join, other languages may call Flatten.
You can always implement Join by using SelectMany with the identity function:
public static IO<T> Join<T>(this IO<IO<T>> source) { return source.SelectMany(x => x); }
In C# the identity function is idiomatically given as the lambda expression x => x since C# doesn't come with a built-in identity function.
Return #
Apart from monadic bind, a monad must also define a way to put a normal value into the monad. Conceptually, I call this function return (because that's the name that Haskell uses). In the IO functor article, I wrote that the IO<T> constructor corresponds to return. That's not strictly true, though, since the constructor takes a Func<T> and not a T.
This issue is, however, trivially addressed:
public static IO<T> Return<T>(T x) { return new IO<T>(() => x); }
Take the value x and wrap it in a lazily-evaluated function.
Laws #
While IO values are referentially transparent you can't compare them. You also can't 'run' them by other means than running a program. This makes it hard to talk meaningfully about the monad laws.
For example, the left identity law is:
return >=> h ≡ h
Note the implied equality. The composition of return and h should be equal to h, for some reasonable definition of equality. How do we define that?
Somehow we must imagine that two alternative compositions would produce the same observable effects ceteris paribus. If you somehow imagine that you have two parallel universes, one with one composition (say return >=> h) and one with another (h), if all else in those two universes were equal, then you would observe no difference in behaviour.
That may be useful as a thought experiment, but isn't particularly practical. Unfortunately, due to side effects, things do change when non-deterministic behaviour and side effects are involved. As a simple example, consider an IO action that gets the current time and prints it to the console. That involves both non-determinism and a side effect.
In Haskell, that's a straightforward composition of two IO actions:
> h () = getCurrentTime >>= print
How do we compare two compositions? By running them?
> return () >>= h 2022-06-25 16:47:30.6540847 UTC > h () 2022-06-25 16:47:37.5281265 UTC
The outputs are not the same, because time goes by. Can we thereby conclude that the monad laws don't hold for IO? Not quite.
The IO Container is referentially transparent, but evaluation isn't. Thus, we have to pretend that two alternatives will lead to the same evaluation behaviour, all things being equal.
This property seems to hold for both the identity and associativity laws. Whether or not you compose with return, or in which evaluation order you compose actions, it doesn't affect the outcome.
For completeness sake, the C# implementation sketch is just a wrapper over a Func<T>. We can also think of such a function as a function from unit to T - in pseudo-C# () => T. That's a function; in other words: The Reader monad. We already know that the Reader monad obeys the monad laws, so the C# implementation, at least, should be okay.
Conclusion #
IO forms a monad, among other abstractions. This is what enables Haskell programmers to compose an arbitrary number of impure actions with monadic bind without ever having to force evaluation. In C# it might have looked the same, except that it doesn't.
Next: Test Data Generator monad.
Adding NuGet packages when offline
A fairly trivial technical detective story.
I was recently in an air plane, writing code, when I realised that I needed to add a couple of NuGet packages to my code base. I was on one of those less-travelled flights in Europe, on board an Embraer E190, and as is usually the case on those 1½-hour flights, there was no WiFi.
Adding a NuGet package typically requires that you're online so that the tools can query the relevant NuGet repository. You'll need to download the package, so if you're offline, you're just out of luck, right?
Fortunately, I'd previously used the packages I needed in other projects, on the same laptop. While I'm no fan of package restore, I know that the local NuGet tools cache packages somewhere on the local machine.
So, perhaps I could entice the tools to reuse a cached package...
First, I simply tried adding a package that I needed:
$ dotnet add package unquote Determining projects to restore... Writing C:\Users\mark\AppData\Local\Temp\tmpF3C.tmp info : X.509 certificate chain validation will use the default trust store selected by .NET. info : Adding PackageReference for package 'unquote' into project '[redacted]'. error: Unable to load the service index for source https://api.nuget.org/v3/index.json. error: No such host is known. (api.nuget.org:443) error: No such host is known.
Fine plan, but no success.
Clearly the dotnet tool was trying to access api.nuget.org, which, obviously, couldn't be reached because my laptop was in flight mode. It occurred to me, though, that the reason that the tool was querying api.nuget.org was that it wanted to see which version of the package was the most recent. After all, I hadn't specified a version.
What if I were to specify a version? Would the tool use the cached version of the package?
That seemed worth a try, but which versions did I already have on my laptop?
I don't go around remembering which version numbers I've used of various NuGet packages, but I expected the NuGet tooling to have that information available, somewhere.
But where? Keep in mind that I was offline, so couldn't easily look this up.
On the other hand, I knew that these days, most Windows applications keep data of that kind somewhere in AppData, so I started spelunking around there, looking for something that might be promising.
After looking around a bit, I found a subdirectory named AppData\Local\NuGet\v3-cache. This directory contained a handful of subdirectories obviously named with GUIDs. Each of these contained a multitude of .dat files. The names of those files, however, looked promising:
list_antlr_index.dat list_autofac.dat list_autofac.extensions.dependencyinjection.dat list_autofixture.automoq.dat list_autofixture.automoq_index.dat list_autofixture.automoq_range_2.0.0-3.6.7.dat list_autofixture.automoq_range_3.30.3-3.50.5.dat list_autofixture.automoq_range_3.50.6-4.17.0.dat list_autofixture.automoq_range_3.6.8-3.30.2.dat list_autofixture.dat ...
and so on.
These names were clearly(?) named list_[package-name].dat or list_[package-name]_index.dat, so I started looking around for one named after the package I was looking for (Unquote).
Often, both files are present, which was also the case for Unquote.
$ ls list_unquote* -l -rw-r--r-- 1 mark 197609 348 Oct 1 18:38 list_unquote.dat -rw-r--r-- 1 mark 197609 42167 Sep 23 21:29 list_unquote_index.dat
As you can tell, list_unquote_index.dat is much larger than list_unquote.dat. Since I didn't know what the format of these files were, I decided to look at the smallest one first. It had this content:
{
"versions": [
"1.3.0",
"2.0.0",
"2.0.1",
"2.0.2",
"2.0.3",
"2.1.0",
"2.1.1",
"2.2.0",
"2.2.1",
"2.2.2",
"3.0.0",
"3.1.0",
"3.1.1",
"3.1.2",
"3.2.0",
"4.0.0",
"5.0.0",
"6.0.0-rc.1",
"6.0.0-rc.2",
"6.0.0-rc.3",
"6.0.0",
"6.1.0"
]
}
A list of versions. Sterling. It looked as though version 6.1.0 was the most recent one on my machine, so I tried to add that one to my code base:
$ dotnet add package unquote --version 6.1.0 Determining projects to restore... Writing C:\Users\mark\AppData\Local\Temp\tmp815D.tmp info : X.509 certificate chain validation will use the default trust store selected by .NET. info : Adding PackageReference for package 'unquote' into project '[redacted]'. info : Restoring packages for [redacted]... info : Package 'unquote' is compatible with all the specified frameworks in project '[redacted]'. info : PackageReference for package 'unquote' version '6.1.0' added to file '[redacted]'. info : Generating MSBuild file [redacted]. info : Writing assets file to disk. Path: [redacted] log : Restored [redacted] (in 397 ms).
Jolly good! That worked.
This way I managed to install all the NuGet packages I needed. This was fortunate, because I had so little time to transfer to my connecting flight that I never got to open the laptop before I was airborne again - in another E190 without WiFi, and another session of offline programming.
Comments
A postscript to your detective story might note that the primary NuGet cache lives at %userprofile%\.nuget\packages on Windows and ~/.nuget/packages on Mac and Linux. The folder names there are much easier to decipher than the folders and files in the http cache.

Comments
CsCheck is a full implementation of something along these lines. It uses the same random sample generation in the shrinking step always reducing a Size measure. It turns out to be a better way of shrinking than the QuickCheck way.
Anthony, thank you for writing. You'll be pleased to learn, I take it, that the next article in the series about the epistemology of interaction testing uses CsCheck as the example framework.