ploeh blog danish software design
A type-safe DI Container C# example
An ultimately pointless exploration of options.
This article is part of a series called Type-safe DI composition. In the previous article, you saw a type-level prototype written in Haskell. If you don't read Haskell code, then it's okay to skip that article and instead start reading here. I'm not going to assume that you've read and understood the previous article.
In this article, I'll begin exploration of a type-safe Dependency Injection (DI) Container prototype written in C#. In order to demonstrate that it works in a realistic environment, I'm going to use it in the code base that accompanies Code That Fits in Your Head.
Empty container #
Like the previous article, we can start with an empty container:
public sealed class Container { public readonly static Container Empty = new Container(); private Container() { } public Container<T1> Register<T1>(T1 item1) { return new Container<T1>(item1); } }
The only API this class affords is the Empty Singleton instance and the Register method. As you can tell from the signature, this method returns a different container type.
Generic container with one item #
The above Register method returns a Container<T1> instance. This class is defined like this:
public sealed class Container<T1> { public Container(T1 item1) { Item1 = item1; } public T1 Item1 { get; } // More members here...
This enables you to add a single service of any type T1. For example, if you Register an IConfiguration instance, you'll have a Container<IConfiguration>:
Container<IConfiguration> container = Container.Empty.Register(Configuration);
The static type system tells you that Item1 contains an IConfiguration object - not a collection of IConfiguration objects, or one that may or may not be there. There's guaranteed to be one and only one. No defensive coding is required:
IConfiguration conf = container.Item1;
A container that contains only a single service is, however, hardly interesting. How do we add more services?
Registration #
The Container<T1> class affords a Register method of its own:
public Container<T1, T2> Register<T2>(T2 item2) { return new Container<T1, T2>(Item1, item2); }
This method return a new container that contains both Item1 and item2.
There's also a convenient overload that, in some scenarios, better support method chaining:
public Container<T1, T2> Register<T2>(Func<T1, T2> create) { if (create is null) throw new ArgumentNullException(nameof(create)); T2 item2 = create(Item1); return Register(item2); }
This method runs a create function to produce an object of the type T2 given the already-registered service Item1.
As an example, the code base's Composition Root defines a method for creating an IRestaurantDatabase object:
public static IRestaurantDatabase CreateRestaurantDatabase( IConfiguration configuration) { if (configuration is null) throw new ArgumentNullException(nameof(configuration)); var restaurantsOptions = configuration.GetSection("Restaurants") .Get<RestaurantOptions[]>(); return new InMemoryRestaurantDatabase(restaurantsOptions .Select(r => r.ToRestaurant()) .OfType<Restaurant>() .ToArray()); }
Notice that this method takes an IConfiguration object as input. You can now use the Register overload to add the IRestaurantDatabase service to the container:
Container<IConfiguration, IRestaurantDatabase> container = Container.Empty .Register(Configuration) .Register(conf => CompositionRoot.CreateRestaurantDatabase(conf));
Or, via eta reduction:
Container<IConfiguration, IRestaurantDatabase> container = Container.Empty
.Register(Configuration)
.Register(CompositionRoot.CreateRestaurantDatabase);
You've probably noticed that this container is one with two generic type arguments.
Generic container with two items #
This new class is, not surprisingly, defined like this:
public sealed class Container<T1, T2> { public Container(T1 item1, T2 item2) { Item1 = item1; Item2 = item2; } public T1 Item1 { get; } public T2 Item2 { get; } public Container<T1, T2, T3> Register<T3>(T3 item3) { return new Container<T1, T2, T3>(Item1, Item2, item3); } public Container<T1, T2, T3> Register<T3>(Func<T1, T2, T3> create) { if (create is null) throw new ArgumentNullException(nameof(create)); var item3 = create(Item1, Item2); return Register(item3); } public override bool Equals(object? obj) { return obj is Container<T1, T2> container && EqualityComparer<T1>.Default.Equals(Item1, container.Item1) && EqualityComparer<T2>.Default.Equals(Item2, container.Item2); } public override int GetHashCode() { return HashCode.Combine(Item1, Item2); } }
Like Container<T1> it also defines two Register overloads that enable you to add yet another service.
If you're on C# 9 or later, you could dispense with much of the boilerplate code by defining the type as a record instead of a class.
Containers of higher arity #
You've probably noticed a pattern. Each Register method just returns a container with incremented arity:
public Container<T1, T2, T3, T4> Register<T4>(T4 item4) { return new Container<T1, T2, T3, T4>(Item1, Item2, Item3, item4); }
and
public Container<T1, T2, T3, T4, T5> Register<T5>(T5 item5) { return new Container<T1, T2, T3, T4, T5>(Item1, Item2, Item3, Item4, item5); }
and so on.
Wait! Does every new service require a new class? What if you have 143 services to register?
Well, yes, as presented here, you'll need 144 classes (one for each service, plus the empty container). They'd all be generic, so you could imagine making a reusable library that defines all these classes. It is, however, pointless for several reasons:
- You shouldn't have that many services. Do yourself a favour and have a service for each 'real' architectural dependency: 1. Database, 2. Email gateway, 3. Third-party HTTP service, etc. Also, add a service for anything else that's not referentially transparent, such as clocks and random number generators. For the example restaurant reservation system, the greatest arity I needed was 5:
Container<T1, T2, T3, T4, T5>. - You don't need a container for each arity after all, as the next article will demonstrate.
- This is all pointless anyway, as already predicted in the introduction article.
Usage #
You can create a statically typed container by registering all the required services:
var container = Container.Empty .Register(Configuration) .Register(CompositionRoot.CreateRestaurantDatabase) .Register(CompositionRoot.CreatePostOffice) .Register(CompositionRoot.CreateClock()) .Register( (c, _, po, __) => CompositionRoot.CreateRepository(c, po));
The container object has the type Container<IConfiguration, IRestaurantDatabase, IPostOffice, IClock, IReservationsRepository>
, which is quite a mouthful. You can, however, pass it to the CompositionRoot and register it as the application's IControllerActivator:
var compositionRoot = new CompositionRoot(container); services.AddSingleton<IControllerActivator>(compositionRoot);
CompositionRoot.Create uses the injected container to create Controllers:
public object Create(ControllerContext context) { if (context is null) throw new ArgumentNullException(nameof(context)); var t = context.ActionDescriptor.ControllerTypeInfo; if (t == typeof(CalendarController)) return new CalendarController( container.Item2, container.Item5); else if (t == typeof(HomeController)) return new HomeController(container.Item2); else if (t == typeof(ReservationsController)) return new ReservationsController( container.Item4, container.Item2, container.Item5); else if (t == typeof(RestaurantsController)) return new RestaurantsController(container.Item2); else if (t == typeof(ScheduleController)) return new ScheduleController( container.Item2, container.Item5, AccessControlList.FromUser(context.HttpContext.User)); else throw new ArgumentException( $"Unexpected controller type: {t}.", nameof(context)); }
Having to refer to Item2, Item5, etc. instead of named services leaves better readability to be desired, but in the end, it doesn't even matter, because, as you'll see as this article series progresses, this is all moot.
Conclusion #
You can define a type-safe DI Container with a series of generic containers. Each registered service has a generic type, so if you need a single IFoo, you register a single IFoo object. If you need a collection of IBar objects, you register an IReadOnlyCollection<IBar>, and so on. This means that you don't have to waste brain capacity remembering the configuration of all services.
Compared to the initial Haskell prototype, the C# example shown here doesn't prevent you from registering the same type more than once. I don't know of a way to do this at the type level in C#, and while you could make a run-time check to prevent this, I didn't implement it. After all, as this article series will demonstrate, none of this is particularly useful, because Pure Di is simpler without being less powerful.
If you were concerned about the proliferation of generic classes with increasing type argument arity, then rest assured that this isn't a problem. The next article in the series will demonstrate how to get around that issue.
Type-level DI Container prototype
A fairly pointless Haskell exercise.
This article is part of a series called Type-safe DI composition.
People sometimes ask me how to do Dependency Injection (DI) in Functional Programming, and the short answer is that you don't. DI makes everything impure, while the entire point of FP is to write as much referentially transparent code as possible. Instead, you should aim for the Functional Core, Imperative Shell style of architecture (AKA impureim sandwich).
Occasionally, someone might point out that you can use the contravariant Reader functor with a 'registry' of services to emulate a DI Container in FP.
Not really, because even if you make the dependencies implicitly available as the Reader 'environment', they're still impure. More on that in a future article, though.
Still, what's a DI Container but a dictionary of objects, keyed by type? After I read Thinking with Types I thought I'd do the exercise and write a type-level container of values in Haskell.
Module #
The TLContainer module requires a smorgasbord of extensions and a few imports:
{-# LANGUAGE AllowAmbiguousTypes #-}
{-# LANGUAGE ConstraintKinds #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE PolyKinds #-}
{-# LANGUAGE GADTs #-}
{-# LANGUAGE ScopedTypeVariables #-}
{-# LANGUAGE TypeApplications #-}
{-# LANGUAGE TypeOperators #-}
{-# LANGUAGE TypeFamilies #-}
{-# LANGUAGE FlexibleContexts #-}
{-# LANGUAGE RankNTypes #-}
{-# LANGUAGE UndecidableInstances #-}
module TLContainer (Container (), nil, insert, get) where
import Data.Kind
import Data.Proxy
import GHC.TypeLits
import Fcf
import Unsafe.Coerce (unsafeCoerce)
Notice that the module only exports the Container type, but not its data constructor. You'll have to use nil and insert to create values of the type.
Data types #
The Container should be able to store an arbitrary number of services of arbitrary types. This doesn't sound like a good fit for a statically typed language like Haskell, but it's possible to do this with existential types. Define an existential type that models a container registration:
data Reg where Reg :: a -> Reg
The problem with existential types is that the type argument a is lost at compile time. If you have a Reg value, it contains a value (e.g. a service) of a particular type, but you don't know what it is.
You can solve this by keeping track of the types at the type level of the container itself. The Container data type is basically just a wrapper around a list of Reg values:
data Container (ts :: [k]) where UnsafeContainer :: [Reg] -> Container ts
The name of the data constructor is UnsafeContainer because it's unsafe. It would enable you to add multiple registrations of the same type. The container shouldn't allow that, so the module doesn't export UnsafeContainer. Instead, it defines sufficient type-level constraints to guarantee that if you try to add two registrations of the same type, your code isn't going to compile.
This is the principal feature that distinguishes Container from the set of tuples that Haskell already defines.
Registration #
The module exports an empty Container:
nil :: Container '[] nil = UnsafeContainer []
Not only is this container empty, it's also statically typed that way. The type Container '[] is isomorphic to ().
The nil container gives you a container so that you can get started. You can add a registration to nil, and that's going to return a new container. You can add another registration to that container, and so on.
The distinguishing feature of Container, however, is that you can only add one registration of a given type. If you want to register multiple services of the same type, register a list of them.
Code like insert readReservations $ insert readReservations nil shouldn't compile, because it tries to insert the same service (readReservations) twice. To enable that feature, the module must be able to detect type uniqueness at the type level. This is possible with the help from the first-class-families package:
type UniqueType (t :: k) (ts :: [k]) = Null =<< Filter (TyEq t) ts
This type models the condition that the type t must not be in the list of types ts. It almost looks like regular Haskell code at the term level, but it works at the type level. Null is a type that can be evaluated to Boolean types at compile-time, depending on whether a list is empty or not.
This enables you to define a closed type family that will produce a compile-time error if a candidate type isn't unique:
type family RequireUniqueType (result :: Bool) (t :: k) :: Constraint where RequireUniqueType 'True t = () RequireUniqueType 'False t = TypeError ( 'Text "Attempting to add the type " ':<>: 'ShowType t ':<>: 'Text " to the container, but this container already contains that type.")
Combined with the UniqueType alias, you can now define the insert function:
insert :: RequireUniqueType (Eval (UniqueType t ts)) t => t -> Container ts -> Container (t ': ts) insert x (UnsafeContainer xs) = UnsafeContainer (Reg x : xs)
This function enables you to register multiple services, like this:
container :: Container '[LocalTime -> IO [Reservation], Reservation -> IO ()] container = insert readReservations $ insert createReservation nil
If, on the other hand, you attempt to register the same service multiple times, your code doesn't compile. You might, for example, attempt to do something like this:
container' = insert readReservations container
When you try to compile your code, however, it doesn't:
* Attempting to add the type LocalTime
-> IO
[Reservation] to the container,
but this container already contains that type.
* In the expression: insert readReservations container
In an equation for container':
container' = insert readReservations container
|
36 | container' = insert readReservations container
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
As a proof of concept, that's good enough for me. A type-safe set of uniquely typed registrations.
Retrieval #
Given that Container is a wrapper over a list of existential types, it seems as though the type information is lost. It isn't, though. Consider the type of the above container value. At the type level, you can see that it contains two services: one with the type LocalTime -> IO [Reservation], and another with the type Reservation -> IO (). Not only that, but the compiler can see the position of each of those types. Due to the way insert is implemented, that order corresponds to the order of Reg values.
First, define a type alias to find the index of a type t in a list of types ts:
type FindElem (t :: k) (ts :: [k]) =
FromMaybe Stuck =<< FindIndex (TyEq t) ts
This is again the first-class-families package in action. FindIndex finds a Nat that represents the index if the type is there. If it isn't there, the type is equivalent to Stuck, which is the type-level equivalent of undefined. Nat is a KnownNat instance, whereas Stuck isn't, which now enables you to define a constraint:
type IsMember t ts = KnownNat (Eval (FindElem t ts))
The IsMember constraint limits t to belong to ts. With it, you can now define a helper function to find the index of a type t in a list of types ts:
findElem :: forall t ts. IsMember t ts => Int findElem = fromIntegral . natVal $ Proxy @(Eval (FindElem t ts))
Because of the IsMember constraint, we know that t must be a member of ts. You can't call findElem if that's not the case; your code wouldn't compile.
You can now define a function to retrieve a service from a Container:
get :: forall t ts. IsMember t ts => Container ts -> t get (UnsafeContainer xs) = unReg $ xs !! findElem @t @ts where unReg (Reg x) = unsafeCoerce x
The get function first finds the index of the type t in ts. It then uses the (unsafe) list index operator !! to get the correct Reg value out of x. While the use of !! is generally considered unsafe (or, at least, partial) in Haskell, we know that the element is there because of the IsMember constraint.
Furthermore, because of the way insert builds up the container, we know that the service inside the existential type Reg must be of the type t. Thus, it's safe to use unsafeCoerce.
Example #
Imagine that you've created the above container. You can now retrieve services from it as necessary.
For example, to implement a HTTP GET resource that returns a list of reservations for a given date, you could do something like this:
getReservations :: LocalTime -> IO (HTTPResult [Reservation]) getReservations date = do let svc = get container :: LocalTime -> IO [Reservation] reservations <- svc date return $ OK reservations
Nothing much happens here. You could imagine that proper input validation of date is done before the service is invoked, or that some mapping operation is done on reservations before the function returns them. I omitted those steps, since they're not what matters. What matters is that that you can use get to safely get a service of the type LocalTime -> IO [Reservation].
Likewise, you could implement an HTTP POST resource that clients can use use to create new reservations:
postReservation :: Reservation -> IO (HTTPResult ()) postReservation dto = do let svc = get container :: Reservation -> IO () svc dto return $ OK ()
Since the compiler knows that container also contains a service of the type Reservation -> IO (), this still compiles.
If, on the other hand, you attempted to implement a single HTTP GET resource, the following wouldn't compile:
getSingleReservation :: LocalTime -> String -> IO (HTTPResult Reservation) getSingleReservation date email = do let svc = get container :: LocalTime -> String -> IO (Maybe Reservation) mres <- svc date email case mres of Just r -> return $ OK r Nothing -> return $ NotFound
The get container line doesn't compile because container doesn't contain a service of the type LocalTime -> String -> IO (Maybe Reservation), and the compiler can tell.
If you truly want to add that feature, you'll have to first register that service with the container:
container :: Container '[ LocalTime -> String -> IO (Maybe Reservation), LocalTime -> IO [Reservation], Reservation -> IO ()] container = insert readReservation $ insert readReservations $ insert createReservation nil
Notice that the type of container has now changed. It now contains three services instead of two. The getSingleReservation action now compiles.
Uniqueness #
The Container shown here is essentially just a glorified tuple. The only distinguishing trait is that you can define a tuple where two or more elements have the same type, such as (String, Bool, String), whereas this isn't possible with Container. You can define a Container '[String, Bool], but not Container '[String, Bool, String].
Why is this desirable?
This stems from a short and (friendly, I hope) Twitter discussion initiated by Bogdan Galiceanu. We were discussing whether it'd be more appropriate to use SingleOrDefault to manipulate a service in a DI Container, or foreach.
"Yeah, I wasn't explicit and clarified in a second tweet. I didn't mean in the services example, but in general where it helps if the reader's mental model of the code has 1 item from the collection, because that's how it is in real life. SingleOrDefault would enforce this."
The point being made here is that while you have a dictionary of collections, you expect certain (if not all) of these collections to be singleton sets.
I'm so happy that people like Bogdan Galiceanu share their thoughts with me, because it gives me a wider perspective on how programmers interact with APIs. If you take the API of the .NET Core DI Container as given, you almost have to think of its entries in this way.
I think, on the other hand, that this indicates a missed opportunity of API design. I replied:
"Yes, this could be a requirement. I think, though, that if that's the case, you've unearthed another invariant. That's what object-oriented design is about.
"Different invariants imply a change of type. If there can only be one of each element, then a set is more appropriate."
Twitter isn't a medium that makes it easy to elaborate on ideas, but what I meant was that if a container should contain only a single instance of, say, IFoo, it'd be clearer if the type system reflected that. Thus, when resolving IFoo, the return type should be IFoo, and not IEnumerable<IFoo>.
On the other hand, if you meant to register a collection of IBar services, when resolving IBar, the return type should be IEnumerable<IBar> (or, even better, IReadOnlyCollection<IBar>).
The Container shown here has this desired property: You can't insert the same type more than once. If you want to insert multiple IBar values, you must insert a [IBar] (list of IBar). Thus, you can't get a single IBar, but you can get a list: [IBar].
That was my motivation for the rule that each type can only appear once. In Haskell it's possible to implement such a rule at the type level. I don't think it'd be possible in a language like C# or F#, but you could implement it as a run-time check.
Conclusion #
You can implement a type-level container of values in Haskell. The contents are completely parametrically polymorphic, so while you can insert pure values like String, Bool, or Reservation into it, you can also add functions and impure actions like Reservation -> IO ().
Why is this interesting? It really isn't, apart from that I found it an interesting exercise in type-level programming.
The idea of a type-safe DI Container is, however, marginally more compelling, so I'll return to that topic in a future article.
Enumerate Wordle combinations with an applicative functor
An example of ad-hoc programming.
Like so many others, I recently started solving the daily Wordle puzzle. As is normal when one is a beginner, I initially struggled a bit. One day, I couldn't find a good word to proceed.
To be clear, this article isn't really about Wordle strategies or tools. Rather, it's an example of ad-hoc programming. Particularly, it's an example of how the applicative nature of lists can be useful when you need to enumerate combinations. While I've previously shown a similar example, I think one more is warranted.
Inured from tears #
Last Monday, I'd started with the word TEARS. (I've subsequently learned that better starting words exist.) The puzzle responded with a yellow E and a green R:

In case you haven't played the game, this means that the fourth letter of the hidden word is an R, and that the word also contains an E. The second letter, however, is not an E. Also, the hidden word contains neither T, A, nor S.
While the green and yellow letters may be repeated, you only have six guesses, so it's a good idea to attempt to exhaust as many letters as possible. The first compatible word with five distinct letters that I could think of was INURE.

This gave me a bit of new information. The hidden word also contains a U, but not as the third letter. Furthermore, the E isn't the last letter either. Keep in mind that from TEARS we also know that E isn't the second letter.
While I believe myself to have a decent English vocabulary, at this point I was stuck. While I knew that the E had to be in either first or third position, I couldn't think of a single word that fit all observations.
After trying to come up with a word for ten minutes, I decided that, instead of giving up, I'd use the applicative nature of lists to generate all possible combinations. I was hoping that with the observations already in place, there wouldn't be too many to sift through.
Combinations #
While you could do this in other languages (such as F# or C#), it's natural to use Haskell because it natively understands applicative functors. Thus, I launched GHCi (Glasgow Haskell Compiler interactive - the Haskell REPL).
Wordle is kind enough to show a keyboard with colour-coded keys:

All letters except the dark ones remain valid, so I first defined a list of all available letters:
> avail = "QWERYUOPDFGHJKLZXCVBM"
The variable avail is a String, but in Haskell, a String is a type synonym for a (linked) list of Char values (characters). Since lists form an applicative functor, that'll work.
Most of the letters are still in play - only five letters are already out of the picture: T, I, A, S, and N. Thus, availstill spells out most of the alphabet.
Next, I wrote an expression that enumerates all five-letter combinations of these letters, with one constraint: The fourth letter must be an R:
> candidates = (\x y z æ ø -> [x,y,z,æ,ø]) <$> avail <*> avail <*> avail <*> "R" <*> avail
The leftmost expression ((\x y z æ ø -> [x,y,z,æ,ø])) is a lambda expression that takes five values (one from each list of available letters) and combines them to a single list. Each value (x, y, and so on) is a Char value, and since String in Haskell is the same as [Char], the expression [x,y,z,æ,ø] is a String. In Danish we have three more letters after z, so I after I ran out of the the usual Latin letters, I just continued with the Danish æ and ø.
Notice that between each of the <*> operators (apply) I've supplied the list of available letters. In the fourth position there's no choice, so there the list contains only a single letter. Recall that a String is a list of characters, so "R" is the same as ['R'].
How many combinations are there? Let's ask GHCi:
> length candidates 194481
Almost 200,000. That's a bit much to look through, but we can peek at the first ten as a sanity check:
> take 10 candidates ["QQQRQ","QQQRW","QQQRE","QQQRR","QQQRY","QQQRU","QQQRO","QQQRP","QQQRD","QQQRF"]
There are no promising words in this little list, but I never expected that.
I needed to narrow down the options.
Filtering #
How do you make a collection smaller? You could filter it.
candidates contains illegal values. For example, the third value in the above list (of the ten first candidates) is "QQQRE". Yet, we know (from the INURE attempt) that the last letter isn't E. We can filter out all strings that end with E:
> take 10 $ filter (\s -> s!!4 /= 'E') candidates ["QQQRQ","QQQRW","QQQRR","QQQRY","QQQRU","QQQRO","QQQRP","QQQRD","QQQRF","QQQRG"]
In Haskell, !! is the indexing operator, so s!!4 means the (zero-based) fourth element of the string s. /= is the inequality operator, so the lambda expression (\s -> s!!4 /= 'E') identifies all strings where the fifth element (or fourth element, when starting from zero) is different from E.
We know more than this, though. We also know that the second element can't be E, and that the third element isn't U, so add those predicates to the filter:
> take 10 $ filter (\s -> s!!1 /= 'E' && s!!2 /= 'U' && s!!4 /= 'E') candidates ["QQQRQ","QQQRW","QQQRR","QQQRY","QQQRU","QQQRO","QQQRP","QQQRD","QQQRF","QQQRG"]
How many are left?
> length $ filter (\s -> s!!1 /= 'E' && s!!2 /= 'U' && s!!4 /= 'E') candidates 168000
Still too many, but we aren't done yet.
Notice that all of the first ten values shown above are invalid. Why? Because the word must contain at least one E, and none of them do. Let's add that predicate:
> take 10 $ filter (\s -> s!!1 /= 'E' && s!!2 /= 'U' && s!!4 /= 'E' && 'E' `elem` s) candidates ["QQERQ","QQERW","QQERR","QQERY","QQERU","QQERO","QQERP","QQERD","QQERF","QQERG"]
The Boolean expression 'E' `elem` s means that the character 'E' must be an element of the string (list) s.
The same rule applies for U:
> take 10 $ filter (\s -> s!!1 /= 'E' && s!!2 /= 'U' && s!!4 /= 'E' && 'E' `elem` s && 'U' `elem` s)
candidates
["QQERU","QWERU","QRERU","QYERU","QUERQ","QUERW","QUERR","QUERY","QUERU","QUERO"]
There's a great suggestion already! The eighth entry spells QUERY! Let's try it:

QUERY was the word of the day!
A bit embarrassing that I couldn't think of query, given that I often discuss Command Query Separation.
Was that just pure luck? How many suggestions are left in the filtered list?
> length $ filter (\s -> s!!1 /= 'E' && s!!2 /= 'U' && s!!4 /= 'E' && 'E' `elem` s && 'U' `elem` s)
candidates
1921
Okay, a bit lucky. If I ask GHCi to display the filtered list in its entirety, no other word jumps out at me, looking like a real word.
Conclusion #
While I admit that I was a bit lucky that QUERY was among the first ten of 1,921 possible combinations, I still find that applicative combinations are handy as an ad-hoc tool. I'm sure there are more elegant ways to solve a problem like this one, but for me, this approach had low ceremony. It was a few lines of code in a terminal. Once I had the answer, I could just close the terminal and no further clean-up was required.
I'm sure other people have other tool preferences, and perhaps you'd like to leave a comment to the effect that you have a better way with Bash, Python, or APL. That's OK, and I don't mind learning new tricks.
I do find this capability of applicative functors to do combinatorics occasionally useful, though.
Type-safe DI composition
DI Containers aren't type-safe. What are the alternatives?
In April 2020 I published an article called Unit bias against collections. My goal with the article was to point out a common cognitive bias. I just happened to use .NET's built-in DI Container as an example because I'd recently encountered a piece of documentation that exhibited the kind of bias I wanted to write about.
This lead to a discussion about the mental model of the DI Container:
"Yeah, I wasn't explicit and clarified in a second tweet. I didn't mean in the services example, but in general where it helps if the reader's mental model of the code has 1 item from the collection, because that's how it is in real life. SingleOrDefault would enforce this."
The point made by Bogdan Galiceanu highlights the incongruity between the container's API and the mental model required to work with it.
IServiceCollection recap #
The API in case belongs to IServiceCollection, which is little more than a collection of ServiceDescriptor objects. Each ServiceDescriptor describes a service, as the name implies.
Given an IServiceCollection you can, for example, register an IReservationsRepository instance:
var connStr = Configuration.GetConnectionString("Restaurant"); services.AddSingleton<IReservationsRepository>(sp => { var logger = sp.GetService<ILogger<LoggingReservationsRepository>>(); var postOffice = sp.GetService<IPostOffice>(); return new EmailingReservationsRepository( postOffice, new LoggingReservationsRepository( logger, new SqlReservationsRepository(connStr))); });
This adds a ServiceDescriptor entry to the collection. (Code examples are from Code That Fits in Your Head.)
Later, you can remove and replace the service for test purposes:
internal sealed class SelfHostedApi : WebApplicationFactory<Startup> { protected override void ConfigureWebHost(IWebHostBuilder builder) { builder.ConfigureServices(services => { services.RemoveAll<IReservationsRepository>(); services.AddSingleton<IReservationsRepository>( new FakeDatabase()); }); } }
Here I use RemoveAll, even though I 'know' there's only one service of that type. Bogdan Galiceanu's argument, if I understand it correctly, is that it'd be more honest to use SingleOrDefault, since we 'know' that there's only one such service.
I don't bring this up to bash on either Bogdan Galiceanu or the IServiceCollection API, but this exchange of ideas provided another example that DI Containers aren't as helpful as you'd think. While they do provide some services, they require significant mental overhead. You have to 'know' that this service has only one instance, while another service may have two implementations, and so on. As the size of both code base and team grows, keeping all such knowledge in your head becomes increasingly difficult.
The promise of object-orientation was always that you shouldn't have to remember implementation details.
Particularly with statically typed programming languages you should be able to surface such knowledge as static type information. What would a more honest, statically typed DI Container look like?
Statically typed containers #
Over a series of articles I'll explore how a statically typed DI Container might look:
- Type-level DI Container prototype
- A type-safe DI Container C# example
- Nested type-safe DI Containers
- A type-safe DI Container as a functor
- A type-safe DI Container as a tuple
- Type-safe DI Containers are redundant
The first of these articles show a Haskell prototype, while the rest of the articles use C#. If you don't care about Haskell, you can skip the first article.
As the title of the last article implies, this exploration only concludes that type-safe DI Containers are isomorphic to Pure DI. I consider Pure DI the simplest of these approaches, suggesting that there's no point in type-safe DI Containers of the kinds shown here.
Conclusion #
Some people like DI Containers. I don't, because they take away type-safety without providing much benefit to warrant the trade-off. A commonly suggested benefit of DI Containers is lifetime management, but you can trivially implement type-safe lifetime management with Pure DI. I don't find that argument compelling.
This article series examines if it's possible to create a 'better' DI Container by making it more type-safe, but I ultimately conclude that there's no point in doing so.
To ID or not to ID
How to model an ID that sometimes must be present, and sometimes not.
I'm currently writing a client library for Criipto that partially implements the actions available on the Fusebit API. This article, however, isn't about the Fusebit API, so even if you don't know what that is, read on. The Fusebit API is just an example.
This article, rather, is about how to model the absence or presence of an Id property.
User example #
The Fusebit API is an HTTP API that, as these things usually do, enables you to create, read, update, and delete resources. One of these is a user. When you create a user, you supply such data as firstName, lastName, and primaryEmail:
POST /v1/account/acc-123/user HTTP/2
authorization: Bearer 938[...]
content-type: application/json
{
"firstName": "Rhea",
"lastName": "Curran",
"primaryEmail": "recurring@example.net"
}
HTTP/2 200
content-type: application/json; charset=utf-8
{
"id": "usr-8babf0cb95d94e6f",
"firstName": "Rhea",
"lastName": "Curran",
"primaryEmail": "recurring@example.net"
}
Notice that you're supposed to POST the user representation without an ID. The response, however, contains an updated representation of the resource that now includes an id. The id (in this example usr-8babf0cb95d94e6f) was created by the service.
To summarise: when you create a new user, you can't supply an ID, but once the user is created, it does have an ID.
I wanted to capture this rule with the F# type system.
Inheritance #
Before we get to the F# code, let's take a detour around some typical C# code.
At times, I've seen people address this kind of problem by having two types: UserForCreation and CreatedUser, or something like that. The only difference would be that CreatedUser would have an Id property, whereas UserForCreation wouldn't. While, at this time, the rule of three doesn't apply yet, such duplication still seems frivolous.
How does an object-oriented programmer address such a problem? By deriving CreatedUser from UserForCreation, of course!
public class CreatedUser : UserForCreation { public string Id { get; set; } }
I'm not too fond of inheritance, and such a design also comes with a built-in flaw: Imagine a method with the signature public CreatedUser Create(UserForCreation user). While such an API design clearly indicates that you don't have to supply an ID, you still can. You can call such a Create method with a CreatedUser object, since CreatedUser derives from UserForCreation.
CreatedUser user = resource.Create(new CreatedUser { Id = "123", FirstName = "Sue", LastName = "Flay", Email = "suoffle@example.org" });
Since CreatedUser contains an ID, this seems to suggest that you can call the Create method with a user with an ID. What would you expected from such a possibility? In the above code example, what would you expect the value of user.Id to be?
It'd be reasonable to expect user.Id to be "123". This seems to indicate that it'd be possible to supply a client-generated user ID, which would then be used instead of a server-generated user ID. The HTTP API, however, doesn't allow that.
Such a design is misleading. It suggests that CreatedUser can be used where UserForCreation is required. This isn't true.
Generic user #
I was aware of the above problem, so I didn't even attempt to go there. Besides, I was writing the library in F#, not C#, and while F# enables inheritance as well, it's not the first modelling option you'd typically reach for.
Instead, my first attempt was to define user data as a generic record type:
type UserData<'a> =
{
Id : 'a
FirstName : string option
LastName : string option
Email : MailAddress option
Identities : Identity list
Permissions : Permission list
}
(The Fusebit API also enables you to supply Identities and Permissions when creating a user. I omitted them from the above C# example code because this detail is irrelevant to the example.)
This enabled me to define an impure action to create a user:
// ApiClient -> UserData<unit> -> Task<Result<UserData<string>, HttpResponseMessage>> let create client (userData : UserData<unit>) = task { let jobj = JObject () userData.FirstName |> Option.iter (fun fn -> jobj.["firstName"] <- JValue fn) userData.LastName |> Option.iter (fun ln -> jobj.["lastName"] <- JValue ln) userData.Email |> Option.iter (fun email -> jobj.["primaryEmail"] <- email |> string |> JValue) jobj.["identities"] <- userData.Identities |> List.map Identity.toJToken |> List.toArray |> JArray jobj.["access"] <- let aobj = JObject () aobj.["allow"] <- userData.Permissions |> List.map Permission.toJToken |> List.toArray |> JArray aobj let json = jobj.ToString Formatting.None let relativeUrl = Uri ("user", UriKind.Relative) let! resp = Api.post client relativeUrl json if resp.IsSuccessStatusCode then let! content = resp.Content.ReadAsStringAsync () let jtok = JToken.Parse content let createdUser = parseUser jtok return Ok createdUser else return Error resp }
Where parseUser is defined like this:
// JToken -> UserData<string> let private parseUser (jobj : JToken) = let uid = jobj.["id"] |> string let fn = jobj.["firstName"] |> Option.ofObj |> Option.map string let ln = jobj.["lastName"] |> Option.ofObj |> Option.map string let email = jobj.["primaryEmail"] |> Option.ofObj |> Option.map (string >> MailAddress) { Id = uid FirstName = fn LastName = ln Email = email Identities = [] Permissions = [] }
Notice that, if we strip away all the noise from the User.create action, it takes a UserData<unit> as input and returns a UserData<string> as output.
Creating a value of a type like UserData<unit> seems a little odd:
let user = { Id = () FirstName = Some "Helen" LastName = Some "Back" Email = Some (MailAddress "hellnback@example.net") Identities = [] Permissions = [] }
It gets the point across, though. In order to call User.create you must supply a UserData<unit>, and the only way you can do that is by setting Id to ().
Not quite there... #
In the Fusebit API, however, the user resource isn't the only resource that exhibits the pattern of requiring no ID on creation, but having an ID after creation. Another example is a resource called a client. Adopting the above design as a template, I also defined ClientData as a generic record type:
type ClientData<'a> =
{
Id : 'a
DisplayName : string option
Identities : Identity list
Permissions : Permission list
}
In both cases, I also realised that the record types gave rise to functors. A map function turned out to be useful in certain unit tests, so I added such functions as well:
module Client = let map f c = { Id = f c.Id DisplayName = c.DisplayName Identities = c.Identities Permissions = c.Permissions }
The corresponding User.map function was similar, so I began to realise that I had some boilerplate on my hands.
Besides, a type like UserData<'a> seems to indicate that the type argument 'a could be anything. The map function implies that as well. In reality, though, the only constructed types you'd be likely to run into are UserData<unit> and UserData<string>.
I wasn't quite happy with this design, after all...
Identifiable #
After thinking about this, I decided to move the generics around. Instead of making the ID generic, I instead made the payload generic by introducing this container type:
type Identifiable<'a> = { Id : string; Item : 'a }
The User.create action now looks like this:
// ApiClient -> UserData -> Task<Result<Identifiable<UserData>, HttpResponseMessage>> let create client userData = task { let jobj = JObject () userData.FirstName |> Option.iter (fun fn -> jobj.["firstName"] <- JValue fn) userData.LastName |> Option.iter (fun ln -> jobj.["lastName"] <- JValue ln) userData.Email |> Option.iter (fun email -> jobj.["primaryEmail"] <- email |> string |> JValue) jobj.["identities"] <- userData.Identities |> List.map Identity.toJToken |> List.toArray |> JArray jobj.["access"] <- let aobj = JObject () aobj.["allow"] <- userData.Permissions |> List.map Permission.toJToken |> List.toArray |> JArray aobj let json = jobj.ToString Formatting.None let relativeUrl = Uri ("user", UriKind.Relative) let! resp = Api.post client relativeUrl json if resp.IsSuccessStatusCode then let! content = resp.Content.ReadAsStringAsync () let jtok = JToken.Parse content let createdUser = parseUser jtok return Ok createdUser else return Error resp }
Where parseUser is defined as:
// JToken -> Identifiable<UserData> let private parseUser (jtok : JToken) = let uid = jtok.["id"] |> string let fn = jtok.["firstName"] |> Option.ofObj |> Option.map string let ln = jtok.["lastName"] |> Option.ofObj |> Option.map string let email = jtok.["primaryEmail"] |> Option.ofObj |> Option.map (string >> MailAddress) let ids = match jtok.["identities"] with | null -> [] | x -> x :?> JArray |> Seq.map Identity.parse |> Seq.toList let perms = jtok.["access"] |> Option.ofObj |> Option.toList |> List.collect (fun j -> j.["allow"] :?> JArray |> Seq.choose Permission.tryParse |> Seq.toList) { Id = uid Item = { FirstName = fn LastName = ln Email = email Identities = ids Permissions = perms } }
The required input to User.create is now a simple, non-generic UserData value, and the successful return value an Identifiable<UserData>. There's no more arbitrary ID data types. The ID is either present as a string or it's absent.
You could also turn the Identifiable container into a functor if you need it, but I've found no need for it so far. Wrapping and unwrapping the payload from the container is easy without supporting machinery like that.
This design is still reusable. The equivalent Client.create action takes a non-generic ClientData value as input and returns an Identifiable<ClientData> value when successful.
C# translation #
There's nothing F#-specific about the above solution. You can easily define Identifiable in C#:
public sealed class Identifiable<T> { public Identifiable(string id, T item) { Id = id; Item = item; } public string Id { get; } public T Item { get; } public override bool Equals(object obj) { return obj is Identifiable<T> identifiable && Id == identifiable.Id && EqualityComparer<T>.Default.Equals(Item, identifiable.Item); } public override int GetHashCode() { return HashCode.Combine(Id, Item); } }
I've here used the explicit class-based syntax to define an immutable class. In C# 9 and later, you can simplify this quite a bit using record syntax instead (which gets you closer to the F# example), but I chose to use the more verbose syntax for the benefit of readers who may encounter this example and wish to understand how it relates to a less specific C-based language.
Conclusion #
When you need to model interactions where you must not supply an ID on create, but representations have IDs when you query the resources, don't reach for inheritance. Wrap the data in a generic container that contains the ID and a generic payload. You can do this in languages that support parametric polymorphism (AKA generics).
Label persistent test data with deletion dates
If you don't clean up after yourself, at least enable others to do so.
I'm currently developing a software library that interacts with a third-party HTTP API to automate creation of various resources at that third party. While I use automated testing to verify that my code works, I still need to run my automation code against the real service once in while. After all, I'd like to verify that I've correctly interpreted the third party's documentation.
I run my tests against a staging environment. The entire purpose of the library is to create resources, so all successful tests leave behind new 'things' in that staging environment.
I'm not the only person who's testing against that environment, so all sorts of test entries accumulate.
Test data accretion #
More than one developer is working with the third-party staging environment. They create various records in the system for test purposes. Often, they forget about these items once the test is complete.
After a few weeks, you have various entries like these:
- Foo test Permit Client
- Fo Permit test client
- Paul Fo client from ..id
- Paul Verify Bar Test Client
- Pauls test
- SomeClient
- michael-template-client
Some of these may be used for sustained testing. Others look suspiciously like abandoned objects.
Does it matter that stuff like this builds up?
Perhaps not, but it bothers my sense of order. If enough stuff builds up, it may also make it harder to find the item you actually need, and rarely, there may be real storage costs associated with the jetsam. But realistically, it just offends my proclivity for tidiness.
Label ephemeral objects explicitly #
While I was testing my library's ability to create new resources, it dawned on me that I could use the records' display names to explicitly label them as temporary.
At first, I named the objects like this:
Test by Mark Seemann. Delete if older than 10 minutes.
While browsing the objects via a web UI (instead of the HTTP API), however, I realised that the creation date wasn't visible in the UI. That makes it hard to identify the actual age.
So, instead, I began labelling the items with a absolute time of safe deletion:
Test by Mark Seemann. Delete after 2021-11-23T13:13:00Z.
I chose to use ISO 8601 Zulu time because it's unambiguous.
Author name #
As you can tell from the above examples, I explicitly named the object Test by Mark Seemann. The word Test indicates to everyone else that this is a test resource. The reason I decided to include my own name was to make it clear to other readers who to contact in case of doubt.
While I find a message like Delete after 2021-11-23T13:13:00Z quite clear, you can never predict how other readers will interpret a text. Thus, I left my name in the title to give other people an opportunity to contact me if they have questions about the record.
Conclusion #
This is just a little pleasantry you can use to make life for a development team a little more agreeable.
You may not always be able to explicitly label a test item. Some records don't have display names, or the name field is too short to allow a detailed, explicit label.
You may also feel that this isn't worth the trouble, and perhaps it isn't.
I usually clean up after having added test data, but sometimes one forgets. When working in a shared environment, I find it considerate to clearly label test data to indicate to others when it's safe to delete it.
Changing your organisation
Or: How do I convince X to adopt Y in software development?
In January 2012 a customer asked for my help with software architecture. The CTO needed to formulate a strategy to deal with increasing demand for bring-your-own-device (BYOD) access to internal systems. Executives brought their iPhones and iPads to work and expected to be able to access and interact with custom-developed and bespoke internal line-of-business applications.
Quite a few of these were running on the Microsoft stack, which was the reason Microsoft Denmark had recommended me.
I had several meetings with the developers responsible for enabling BYOD. One guy, in particular, kept suggesting a Silverlight solution. I pointed out that Silverlight wouldn't run on Apple devices, but he wouldn't be dissuaded. He was certain that this was the correct solution, and I could tell that he became increasingly frustrated with me because he couldn't convince me.
We'll return to this story later in this essay.
Please convince my manager #
Sometimes people ask me questions like these:
- How do I convince my manager to let me use F#?
- How do I convince my team mates to adopt test-driven development?
- How do I convince the entire team that code quality matters?
Sometimes I receive such questions via email. Sometimes people ask me at conferences or user groups.
To quote Eric Lippert: Why are you even asking me?
To be fair, I do understand why people ask me, but I have few good answers.
Why ask me? #
I suppose people ask me because I've been writing about software improvement for decades. This blog dates back to January 2009, and my previous MSDN blog goes back to January 2006. These two resources alone contain more than 700 posts, the majority of which are about some kind of suggested improvement. Granted, there's also the occasional rant, by I think it's fair to say that my main motivation for writing is to share with readers what I think is right and good.
I do write a lot about potential improvements to software development.
As most readers have discovered, my book about Dependency Injection (with Steven van Deursen) is more than just a manual to a few Dependency Injection Containers, and my new book Code That Fits in Your Head is full of suggested improvements.
Add to that my Pluralsight courses, my Clean Coders videos, and my conference talks, and there's a clear pattern to most of my content.
Maven #
In The Tipping Point Malcolm Gladwell presents a model for information dissemination, containing three types of people required for an idea to take hold: Connectors, mavens, and salesmen.
In that model, a maven is an 'information specialist' - someone who accumulates knowledge and shares it with others. If I resemble any of these three types of people, I'm a maven. I like learning and discovering new ways of doing things, and obviously I like sharing that information. I wouldn't have blogged consistently for sixteen years if I didn't feel compelled to do so.
My role, as I see it, is to find and discover better ways of writing software. Much of what I write about is something that I've picked up somewhere else, but I try to present it in my own way, and I'm diligent about citing sources.
When people ask me concrete questions, like how do I refactor this piece of code? or how do write this in a more functional style?, I present an answer (if I can).
The suggestions I make are just that: It's a buffet of possible solutions to certain problems. If you encounter one of my articles and find the proposed technique useful, then that makes me happy and proud.
Notice the order of events: Someone has a problem, finds my content, and decides that it looks like a solution. Perhaps (s)he remembers my name. Perhaps (s)he feels that I helped solve a problem.
Audience members that come to my conference talks, or readers who buy my books, may not have a concrete problem to solve, but they still voluntarily seeks me out - perhaps because of previous exposure to my content.
To reiterate:
- You have a problem (concrete or vague)
- Perhaps you come across my content
- Perhaps you find it useful
Perhaps you think that I convinced you that 'my way' is best. I didn't. You were already looking for a solution. You were ready for a change. You were open.
Salesman #
When you ask me about how to convince your manager, or your team mates, you're no longer asking me a technical question. Now you're asking about how to win friends and influence people. You don't need a maven for that; you need a salesman. That's not me.
I've had some success applying changes to software organisations, but in all cases, the reason I was there in the first place was because the organisation itself (or members thereof) had asked me to come and help them. When people want your help changing things, convincing them to try something new isn't a hard sell.
When I consult development teams, I'm not there to sell them new processes; I'm there to help them use appropriate solutions at opportune moments.
I'm not a salesman. Just because I convinced you that, say, property-based testing is a good idea doesn't mean I can convince anyone else. Keep in mind that I probably convinced you because you were ready for a change.
Your manager or your team mates may not be.
Bide your time #
While I'm no salesman, I've managed to turn people around from time to time. The best strategy, I've found, is to wait for an opportunity.
As long as everything is going well, people aren't ready to change.
"Only a crisis - actual or perceived - produces real change. When that crisis occurs, the actions that are taken depend on the ideas that are lying around. That, I believe, is our basic function: to develop alternatives to existing policies, to keep them alive and available until the politically impossible becomes the politically inevitable"
If you have solutions at the ready, you may be able to convince your manager or your colleagues to try something new if a crisis occurs. Don't gloat - just present your suggestion: What if we did this instead?
Vocabulary #
Indeed, I'm not a salesman, and while I can't tell you how to sell an idea to an unwilling audience, I can tell you how you can weaken your position: Make it all about you.
Notice how questions like the above are often phrased: my manager will not let me... or how do I convince my colleagues?
I actually didn't much like How to Win Friends and Influence People, but it does present the insight that in order to sway people, you have to consider what's in it for them.
I had to be explicitly told this before I learned that lesson.
In the second half of the 2000s I was attached to a software development project at a large Danish company. After a code review, I realised that the architecture of the code was all wrong!
In order to make the project manager aware of the issue, I wrote an eight-page internal 'white paper' and emailed it to the project manager (let's call him Henk).
Nothing happened. No one addressed the problem.
A few weeks later, I had a scheduled one-on-one meeting with my own manager in Microsoft, and when asked if I had any issues, I started to complain about this problem I'd identified.
My manager looked at me for a moment and asked me: How do you think receiving that email made Henk feel?
It had never crossed my mind to think about that. It was my problem! I discovered it! I viewed myself as a great programmer and architect because I had perceived such a complex issue and was able to describe it clearly. It was all about me, me, me.
When we programmers ask how to convince our managers to 'let us' use TDD, or FP, or some other 'cool' practice, we're still focused on us. What's in it for the manager?
When we talk about code quality and lack thereof, 'ugly code', refactoring, and other such language, a non-coding manager is likely to see us as primadonnas out of touch with reality: We have features to ship, but the programmers only care about making the code 'pretty'.
I offer no silver bullet to convince other people that certain techniques are superior, but do consider introducing suggestions by describing the benefits they bring: Wouldn't it be cool if we could decrease our testing phase from three weeks to three days?, Wouldn't it be nice if we could deploy every week?, Wouldn't it be nice if we could decrease the number of errors our users encounter?
You could be wrong #
Have you ever felt frustrated that you couldn't convince other people to do it your way, despite knowing that you were right?
Recall the developer from the introduction, the one who kept insisting that Silverlight was the right solution to the organisation's BYOD problem. He was clearly convinced that he had the solution, and he was frustrated that I kept rejecting it.
We may scoff at such obvious ignorance of facts, but he had clearly drunk the Microsoft Kool-Aid. I could tell, because I'd been there myself. When you're a young programmer, you may easily buy into a compelling narrative. Microsoft evangelists were quite good at their game back then, as I suppose their Apple and Linux counterparts were and are. As an inexperienced developer, you can easily be convinced that a particular technology will solve all problems.
When you're young and inexperienced, you can easily feel that you're absolutely right and still be unequivocally wrong.
Consider this the next time you push your agenda. Perhaps your manager and colleagues reject your ideas because they're actually bad. A bit of metacognition is often appropriate.
Conclusion #
How do you convince your manager or team mates to do things better?
I don't know; I'm not a salesman, but in this essay, I've nonetheless tried to reflect on the question. I think it helps to consider what the other party gains from accepting a change, but I also think it's a waiting game. You have to be patient.
As an economist, I could also say much about incentives, but this essay is already long enough as it is. Still, when you consider how your counterparts react to your suggestions, reflect on how they are incentivised.
Even if you do everything right, make the best suggestions at the most opportune times, you may find yourself in a situation systemically rigged against doing the right thing. Ultimately, as Martin Fowler quipped, either change your organisation, or change your organisation.
Backwards compatibility as a profunctor
In order to keep backwards compatibility, you can weaken preconditions or strengthen postconditions.
Like the previous articles on Postel's law as a profunctor and the Liskov Substitution Principle as a profunctor, this article is part of a series titled Some design patterns as universal abstractions. And like the previous articles, it's a bit of a stretch including the present article in that series, since backwards compatibility isn't a design pattern, but rather a software design principle or heuristic. I still think, however, that the article fits the spirit of the article series, if not the letter.
Backwards compatibility is often (but not always) a desirable property of a system. Even in Zoo software, it pays to explicitly consider versioning. In order to support Continuous Delivery, you must be able to evolve a system in such a way that it's always in a working state.
When other systems depend on a system, it's important to maintain backwards compatibility. Evolve the system, but support legacy dependents as well.
Adding new test code #
In Code That Fits in Your Head, chapter 11 contains a subsection on adding new test code. Despite admonitions to the contrary, I often experience that programmers treat test code as a second-class citizen. They casually change test code in a more undisciplined way than they'd edit production code. Sometimes, that may be in order, but I wanted to show that you can approach the task of editing test code in a more disciplined way. After all, the more you edit tests, the less you can trust them.
After a preliminary discussion about adding entirely new test code, the book goes on to say:
You can also append test cases to a parametrised test. If, for example, you have the test cases shown in listing 11.1, you can add another line of code, as shown in listing 11.2. That’s hardly dangerous.
Listing 11.1 A parametrised test method with three test cases. Listing 11.2 shows the updated code after I added a new test case. (Restaurant/b789ef1/Restaurant.RestApi.Tests/ReservationsTests.cs)
[Theory] [InlineData(null, "j@example.net", "Jay Xerxes", 1)] [InlineData("not a date", "w@example.edu", "Wk Hd", 8)] [InlineData("2023-11-30 20:01", null, "Thora", 19)] public async Task PostInvalidReservation(Listing 11.2 A test method with a new test case appended, compared to listing 11.1. The line added is highlighted. (Restaurant/745dbf5/Restaurant.RestApi.Tests/ReservationsTests.cs)
[Theory] [InlineData(null, "j@example.net", "Jay Xerxes", 1)] [InlineData("not a date", "w@example.edu", "Wk Hd", 8)] [InlineData("2023-11-30 20:01", null, "Thora", 19)] [InlineData("2022-01-02 12:10", "3@example.org", "3 Beard", 0)] public async Task PostInvalidReservation(You can also add assertions to existing tests. Listing 11.3 shows a single assertion in a unit test, while listing 11.4 shows the same test after I added two more assertions.
Listing 11.3 A single assertion in a test method. Listing 11.4 shows the updated code after I added more assertions. (Restaurant/36f8e0f/Restaurant.RestApi.Tests/ReservationsTests.cs)
Assert.Equal( HttpStatusCode.InternalServerError, response.StatusCode);Listing 11.4 Verification phase after I added two more assertions, compared to listing 11.3. The lines added are highlighted. (Restaurant/0ab2792/Restaurant.RestApi.Tests/ReservationsTests.cs)
Assert.Equal( HttpStatusCode.InternalServerError, response.StatusCode); Assert.NotNull(response.Content); var content = await response.Content.ReadAsStringAsync(); Assert.Contains( "tables", content, StringComparison.OrdinalIgnoreCase);These two examples are taken from a test case that verifies what happens if you try to overbook the restaurant. In listing 11.3, the test only verifies that the HTTP response is
500 Internal Server Error. The two new assertions verify that the HTTP response includes a clue to what might be wrong, such as the messageNo tables available.I often run into programmers who’ve learned that a test method may only contain a single assertion; that having multiple assertions is called Assertion Roulette. I find that too simplistic. You can view appending new assertions as a strengthening of postconditions. With the assertion in listing 11.3 any
500 Internal Server Errorresponse would pass the test. That would include a 'real' error, such as a missing connection string. This could lead to false negatives, since a general error could go unnoticed.Adding more assertions strengthens the postconditions. Any old
500 Internal Server Errorwill no longer do. The HTTP response must also come with content, and that content must, at least, contain the string"tables".This strikes me as reminiscent of the Liskov Substitution Principle. There are many ways to express it, but in one variation, we say that subtypes may weaken preconditions and strengthen postconditions, but not the other way around. You can think of of subtyping as an ordering, and you can think of time in the same way, as illustrated by figure 11.1. Just like a subtype depends on its supertype, a point in time 'depends' on previous points in time. Going forward in time, you’re allowed to strengthen the postconditions of a system, just like a subtype is allowed to strengthen the postcondition of a supertype.
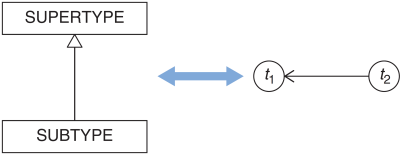
Figure 11.1 A type hierarchy forms a directed graph, as indicated by the arrow from subtype to supertype. Time, too, forms a directed graph, as indicated by the arrow from t2 to t1. Both present a way to order elements.
Think of it another way, adding new tests or assertions is fine; deleting tests or assertions would weaken the guarantees of the system. You probably don’t want that; herein lie regression bugs and breaking changes.
The book leaves it there, but I find it worthwhile to expand on that thought.
Function evolution over time #
As in the previous articles about x as a profunctor, let's first view 'a system' as a function. As I've repeatedly suggested, with sufficient imagination, every operation looks like a function. Even an HTTP POST request, as suggested in the above test snippets, can be considered a function, albeit one with the IO effect.
You can envision a function as a pipe. In previous articles, I've drawn horizontal pipes, with data flowing from left to right, but we can also rotate them 90° and place them on a timeline:
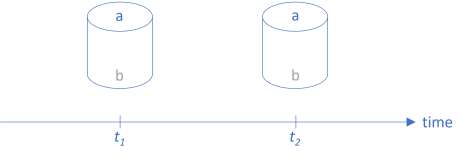
As usually depicted in Western culture, time moves from left to right. In a stable system, functions don't change: The function at t1 is equal to the function at t2.
The function in the illustration takes values belonging to the set a as input and returns values belonging to the set b as output. A bit more formally, we can denote the function as having the type a -> b.
We can view the passing of time as a translation of the function a -> b at t1 to a -> b at t2. If we just leave the function alone (as implied by the above figure), it corresponds to mapping the function with the identity function.
Clients that rely on the function are calling it by supplying input values from the set a. In return, they receive values from the set b. As already discussed in the article about Postel's law as a profunctor, we can illustrate such a fit between client and function as snugly fitting pipes:
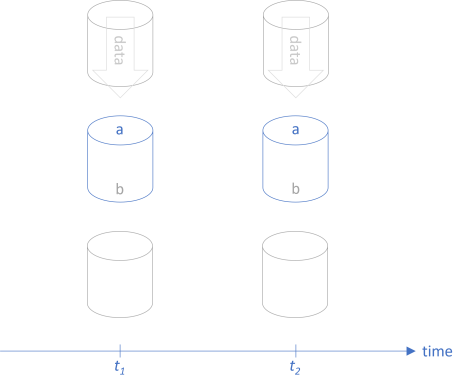
As long as the clients keep supplying elements from a and expecting elements from b in return, the function remains compatible.
If we have to change the function, which kind of change will preserve compatibility?
We can make the function accept a wider set of input, and let it return narrower set of output:
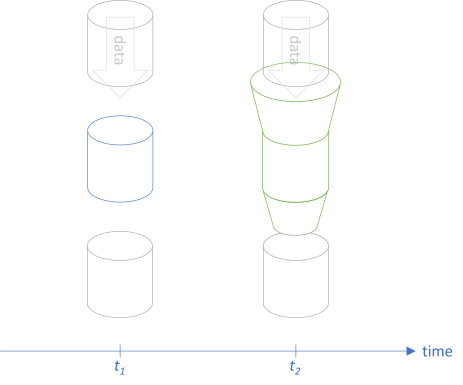
This will not break any existing clients, because they'll keep calling the function with a input and expecting b output values. The drawing is similar to the drawings from the articles on Postel's law as a profunctor and The Liskov Substitution Principle as a profunctor. It seems reasonable to consider backwards compatibility in the same light.
Profunctor #
Consider backwards compatible function evolution as a mapping of a function a -> b at t1 to a' -> b' at t2.
What rules should we institute for this mapping?
In order for this translation to be backwards compatible, we must be able to translate the larger input set a' to a; that is: a' -> a. That's the top flange in the above figure.
Likewise, we must be able to translate the original output set b to the smaller b': b -> b'. That's the bottom nozzle in the above figure.
Thus, armed with the two functions a' -> a and b -> b', we can translate a -> b at t1 to a' -> b' at t2 in a way that preserves backwards compatibility. More formally:
(a' -> a) -> (b -> b') -> (a -> b) -> (a' -> b')
This is exactly the definition of dimap for the Reader profunctor!
Arrow directions #
That's why I wrote as I did in Code That Fits in Your Head. The direction of the arrows in the book's figure 11.1 may seem counter-intuitive, but I had them point in that direction because that's how most readers are used to see supertypes and subtypes depicted.
When thinking of concepts such as Postel's law, it may be more intuitive to think of the profunctor as a mapping from a formal specification a -> b to the more robust implementation a' -> b'. That is, the arrow would point in the other direction.
Likewise, when we think of the Liskov Substitution Principle as rule about how to lawfully derive subtypes from supertypes, again we have a mapping from the supertype a -> b to the subtype a' -> b'. Again, the arrow direction goes from supertype to subtype - that is, in the opposite direction from the book's figure 11.1.
This now also better matches how we intuitively think about time, as flowing from left to right. The arrow, again, goes from t1 to t2.
Most of the time, the function doesn't change as time goes by. This corresponds to the mapping dimap id id - that is, applying the identity function to the mapping.
Implications for tests #
Consider the test snippets shown at the start of the article. When you add test cases to an existing test, you increase the size of the input set. Granted, unit test inputs are only samples of the entire input set, but it's still clear that adding a test case increases the input set. Thus, we can view such an edit as a mapping a -> a', where a ⊂ a'.
Likewise, when you add more assertions to an existing set of assertions, you add extra constraints. Adding an assertion implies that the test must pass all of the previous assertions, as well as the new one. That's a Boolean and, which implies a narrowing of the allowed result set (unless the new assertion is a tautological assertion). Thus, we can view adding an assertion as a mapping b -> b', where b' ⊂ b.
This is why it's okay to add more test cases, and more assertions, to an existing test, whereas you should be weary of the opposite: It may imply (or at least allow) a breaking change.
Conclusion #
As Michael Feathers observed, Postel's law seems universal. That's one way to put it.
Another way to view it is that Postel's law is a formulation of a kind of profunctor. And it certainly seems as though profunctors pop up here, there, and everywhere, once you start looking for that idea.
We can think of the Liskov Substitution Principle as a profunctor, and backwards compatibility as well. It seems reasonable enough: In order to stay backwards compatible, a function can become more tolerant of input, or more conservative in what it returns. Put another way: Contravariant in input, and covariant in output.
The Liskov Substitution Principle as a profunctor
With a realistic example in C#.
Like the previous article on Postel's law as a profunctor, this article is part of a series titled Some design patterns as universal abstractions. And like the previous article, it's a bit of a stretch to include the present article in that series, since the Liskov Substitution Principle (LSP) isn't a design pattern, but rather a software design principle or heuristic. I still think, however, that the article fits the spirit of the article series, if not the letter.
As was also the case for the previous article, I don't claim that any of this is new. Michael Feathers and Rúnar Bjarnason blazed that trail long before me.
LSP distilled #
In more or less natural language, the LSP states that subtypes must preserve correctness. A subtype isn't allowed to change behaviour in such a way that client code breaks.
Note that subtypes are allowed to change behaviour. That's often the point of subtyping. By providing a subtype, you can change the behaviour of a system. You can, for example, override how messages are sent, so that an SMS becomes a Slack notification or a Tweet.
If client code 'originally' supplied correct input for sending an SMS, this input should also be valid for posting a Tweet.
Specifically (paraphrasing the Wikipedia entry as of early November 2021):
- Subtypes must be contravariant in input
- Subtypes must be covariant in output
- Preconditions must not be strengthened in the subtype
- Postconditions must not be weakened in the subtype
There's a bit more, but in this article, I'll focus on those rules. The first two we already know. Since any function is already a profunctor, we know that functions are contravariant in input and covariant in output.
The LSP, however, isn't a rule about a single function. Rather, it's a rule about a family of functions. Think about a function a -> b as a pipe. You can replace the pipe segment with another pipe segment that has exactly the same shape, but replacing it with a flanged pipe also works, as long as the input flange is wider, and the nozzle narrower than the original pipe shape.
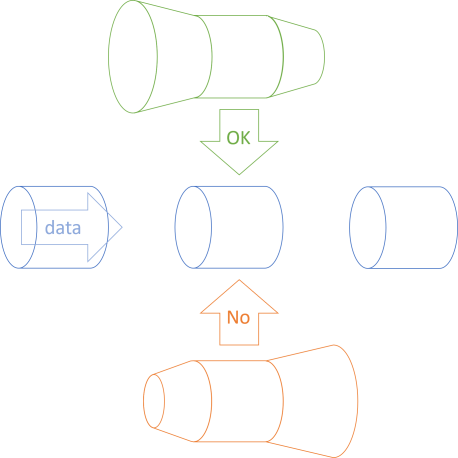
On the other hand, if you narrow the pipe at the input and widen it at the output, spillage will happen. That's essentially what the LSP states: The upper, green, flanged pipe is a good replacement for the supertype (the blue pipe in the middle), while the lower, orange, flanged pipe is not useful.
The previous article already described that visual metaphor when it comes to co- and contravariance, so this article will focus on pre- and postconditions. My conjecture is that this is just another take on co- and contravariance.
Supertype example #
When encountering statements about subtypes and supertypes, most people tend to think about object inheritance, but that's just one example. As I've previously outlined, anything that can 'act as' something else is a subtype of that something else. Specifically, an interface implementation is a subtype of the interface, and the interface itself the supertype.
Consider, as a supertype example, this interface from my book Code That Fits in Your Head:
public interface IReservationsRepository { Task Create(int restaurantId, Reservation reservation); Task<IReadOnlyCollection<Reservation>> ReadReservations( int restaurantId, DateTime min, DateTime max); Task<Reservation?> ReadReservation(int restaurantId, Guid id); Task Update(int restaurantId, Reservation reservation); Task Delete(int restaurantId, Guid id); }
Specifically, in this article, I'll focus exclusively on the ReadReservations method. You can imagine that there's an interface with only that method, or that when subtyping the interface in the following, we vary only that method and keep everything else fixed.
What might be the pre- and postconditions of the ReadReservations method?
ReadReservations preconditions #
The most basic kind of precondition is captured by the parameter types. In order to be able to call the method, you must supply an int and two DateTime instances. You can't omit any of them or replace one of the DateTime values with a Guid. In a statically typed language, this is obvious, and the compiler will take care of that.
Both int and DateTime are value types (structs), so they can't be null. Had one of the parameters been a reference type, it'd be appropriate to consider whether or not null constitutes valid input.
So far, we've only discussed static types. Of course a subtype must satisfy the compiler, but what other pre-conditions might be implied by ReadReservations?
The purpose of the method is to enable client code to query a data store and retrieve the reservations for a particular restaurant and in a particular time interval.
Is any restaurantId acceptable? 1? 0? -235?
It's probably a distraction that the restaurant ID is even an int. After all, you don't add IDs together, or multiply one with another one. That an ID is an integer is really just a leaky implementation detail - databases like it best when IDs are integers. I should actually have defined the restaurant ID as an opaque object with Value Object semantics, but I didn't (like other humans, I'm imperfect and lazy). The bottom line is that any number is as good as any other number. No precondition there.
What about the two DateTime parameters? Are DateTime.MinValue or DateTime.MaxValue valid values? Probably: If you'd like to retrieve all reservations in the past, you could ask for DateTime.MinValue as min and DateTime.Now as max. On the other hand, it'd be reasonable to require that min should be less than (or equal to?) max. That sounds like a proper precondition, and one that's difficult to express as a type.
We may also consider it a precondition that the object that implements the ReadReservations method is properly initialised, but I'll take that as a given. Making sure of that is the responsibility of the constructor, not the ReadReservations method.
To summarise, apart from the types and other things handled by the compiler, there's only one additional pre-condition: that min must be less than max.
Are there any postconditions?
ReadReservations postconditions #
The code base for the book obeys Command-Query Separation. Since ReadReservations returns data, it must be a Query. Thus, we can assume that calling it isn't supposed to change state. Thus, postconditions can only be statements about the return value.
Again, static typing takes care of the most fundamental postconditions. An implementation can't return a double or an UriBuilder. It must be a Task, and that task must compute an IReadOnlyCollection<Reservation>.
Why IReadOnlyCollection, by the way? That's my attempt at describing a particular postcondition as a type.
The IReadOnlyCollection<T> interface is a restriction of IEnumerable<T> that adds a Count. By adding the Count property, the interface strongly suggests that the collection is finite.
IEnumerable<T> implementations can be infinite sequences. These can be useful as functional alternatives to infinite loops, but are clearly not appropriate when retrieving reservations from a database.
The use of IReadOnlyCollection tells us about a postcondition: The collection of reservations is finite. This is, however, captured by the type. Any valid implementation of the interface ought to make that guarantee.
Is there anything else? Is it okay if the collection is empty? Yes, that could easily happen, if you have no reservations in the requested interval.
What else? Not much comes to mind, only that we'd expect the collection to be 'stable'. Technically, you could implement the GetEnumerator method so that it generates Count random Reservation objects every time you enumerate it, but none of the built-in implementations do that; that's quite a low bar, as postconditions go.
To summarise the postconditions: None, apart from a well-behaved implementation of IReadOnlyCollection<Reservation>.
SQL implementation #
According to the LSP, a subtype should be allowed to weaken preconditions. Keep in mind that I consider an interface implementation a subtype, so every implementation of ReadReservations constitutes a subtype. Consider the SQL Server-based implementation:
public async Task<IReadOnlyCollection<Reservation>> ReadReservations( int restaurantId, DateTime min, DateTime max) { var result = new List<Reservation>(); using var conn = new SqlConnection(ConnectionString); using var cmd = new SqlCommand(readByRangeSql, conn); cmd.Parameters.AddWithValue("@RestaurantId", restaurantId); cmd.Parameters.AddWithValue("@Min", min); cmd.Parameters.AddWithValue("@Max", max); await conn.OpenAsync().ConfigureAwait(false); using var rdr = await cmd.ExecuteReaderAsync().ConfigureAwait(false); while (await rdr.ReadAsync().ConfigureAwait(false)) result.Add(ReadReservationRow(rdr)); return result.AsReadOnly(); } private const string readByRangeSql = @" SELECT [PublicId], [At], [Name], [Email], [Quantity] FROM [dbo].[Reservations] WHERE [RestaurantId] = @RestaurantId AND @Min <= [At] AND [At] <= @Max";
This implementation actually doesn't enforce the precondition that min ought to be less than max. It doesn't have to, since the code will run even if that's not the case - the result set, if min is greater than max, will always be empty.
While perhaps not useful, weakening this precondition doesn't adversely affect well-behaved clients, and buggy clients are always going to receive empty results. If this implementation also fulfils all postconditions, it's already LSP-compliant.
Still, could it weaken preconditions even more, or in a different way?
Weakening of preconditions #
As Postel's law suggests, a method should be liberal in what it accepts. If it understands 'what the caller meant', it should perform the desired operation instead of insisting on the letter of the law.
Imagine that you receive a call where min is midnight June 6 and max is midnight June 5. While wrong, what do you think that the caller 'meant'?
The caller probably wanted to retrieve the reservations for June 5.
You could weaken that precondition by swapping back min and max if you detect that they've been swapped.
Let's assume, for the sake of argument, that we make the above ReadReservations implementation virtual. This enables us to inherit from SqlReservationsRepository and override the method:
public override Task<IReadOnlyCollection<Reservation>> ReadReservations( int restaurantId, DateTime min, DateTime max) { if (max < min) return base.ReadReservations(restaurantId, max, min); return base.ReadReservations(restaurantId, min, max); }
While this weakens preconditions, it breaks no existing clients because they all 'know' that they must pass the lesser value before the greater value.
Strengthening of postconditions #
Postel's law also suggests that a method should be conservative in what it sends. What could that mean?
In the case of ReadReservations, you may notice that the result set isn't explicitly sorted. Perhaps we'd like to also sort it on the date and time:
public override async Task<IReadOnlyCollection<Reservation>> ReadReservations( int restaurantId, DateTime min, DateTime max) { var query = min < max ? base.ReadReservations(restaurantId, min, max) : base.ReadReservations(restaurantId, max, min); var reservations = await query.ConfigureAwait(false); return reservations.OrderBy(r => r.At).ToList(); }
This implementation retains the weakened precondition from before, but now it also explicitly sorts the reservations on At.
Since no client code relies on sorting, this breaks no existing clients.
While the behaviour changes, it does so in a way that doesn't violate the original contract.
Profunctor #
While we've used terms such as weaken preconditions and strengthen postconditions, doesn't this look an awful lot like co- and contravariance?
I think it does, so let's rewrite the above implementation using the Reader profunctor.
First, we'll need to express the original method in the shape of a function like a -> b - that is: a function that takes a single input and returns a single output. While ReadReservations return a single value (a Task), it takes three input arguments. To make it fit the a -> b mould, we have to convert those three parameters to a Parameter Object.
This enables us to write the original implementation as a function:
Func<QueryParameters, Task<IReadOnlyCollection<Reservation>>> imp = q => base.ReadReservations(q.RestaurantId, q.Min, q.Max);
If we didn't want to weaken any preconditions or strengthen any postconditions, we could simply call imp and return its output.
The above weakened precondition can be expressed like this:
Func<QueryParameters, QueryParameters> pre = q => q.Min < q.Max ? new QueryParameters(q.RestaurantId, q.Min, q.Max) : new QueryParameters(q.RestaurantId, q.Max, q.Min);
Notice that this is a function from QueryParameters to QueryParameters. As above, it simply swaps Min and Max if required.
Likewise, we can express the strengthened postcondition as a function:
Func<Task<IReadOnlyCollection<Reservation>>, Task<IReadOnlyCollection<Reservation>>> post = t => t.Select(rs => rs.OrderBy(r => r.At).ToReadOnly());
The Select method exists because Task forms an asynchronous functor.
It's now possible to compose imp with pre and post using DiMap:
Func<QueryParameters, Task<IReadOnlyCollection<Reservation>>> composition = imp.DiMap(pre, post);
You can now call composition with the original arguments:
composition(new QueryParameters(restaurantId, min, max))
The output of such a function call is entirely equivalent to the above, subtyped ReadReservations implementation.
In case you've forgotten, the presence of a lawful DiMap function is what makes something a profunctor. We already knew that functions are profunctors, but now we've also seen that we can use this knowledge to weaken preconditions and strengthen postconditions.
It seems reasonable to conjecture that the LSP actually describes a profunctor.
It seems to me that the profunctor composition involved with the LSP always takes the specialised form where, for a function a -> b, the preprocessor (the contravariant mapping) always takes the form a -> a, and the postprocessor (the covariant mapping) always takes the form b -> b. This is because polymorphism must preserve the shape of the original function (a -> b).
Conclusion #
We already know that something contravariant in input and covariant in output is a profunctor candidate, but the Liskov Substitution Principle is usually expressed in terms of pre- and postconditions. Subtypes may weaken preconditions and strengthen postconditions, but not the other way around.
Evidence suggests that you can phrase these rules as a profunctor specialisation.
Comments
It seems to me that the profunctor composition involved with the LSP always takes the specialised form where, for a functiona -> b, the preprocessor (the contravariant mapping) always takes the forma -> a, and the postprocessor (the covariant mapping) always takes the formb -> b. This is because polymorphism must preserve the shape of the original function (a -> b).
I think this depends on the language and your perspective on subtype polymorphism. In Java, a subclass Y of a superclass X can override a method m on X that has return type b with a method on Y that has return type c provided c is a subtype of b. To be clear, I am not saying that the instance returned from Y::m can have runtime-type c, though that is also true. I am saying that the compile-time return type of Y::m can be c.
With this in mind, I am willing to argue that the postprocessor can take the form b -> c provided c is a subtype of b. As the programmer, that is how I think of Y::m. And yet, if someone has a instance of Y with compile-time type X, then calling m returns something with compile-time type b by composing my b -> c function with the natural c -> b function from subtype polymorphism to get the b -> b function that you suggested is required.
Tyson, thank you for writing. Yes, true, that nuance may exist. This implies that the LSP is recursive, which really isn't surprising.
A function a -> b may be defined for types a and b, where both are, themselves, polymorphic. So, if a is HttpStyleUriParser and b is MemberInfo, we'd have a function Func<HttpStyleUriParser, MemberInfo> (or HttpStyleUriParser -> MemberInfo if we want to stick with an ML-style type signature - we can imagine that it's an F# function).
If Func<HttpStyleUriParser, MemberInfo> is our polymorphic target signature, according to C# co- and contravariance, we're allowed to vary both input and output. We can, for example, widen the input type to UriParser and restrict the output type to Type. Thus, a specific function of the type Func<UriParser, Type> is compatible with a general function of the type Func<HttpStyleUriParser, MemberInfo>:
Func<HttpStyleUriParser, MemberInfo> general = specific;
Thus, you're correct that both pre- and postprocessor may take the form a' -> a and b -> b', where a' is a supertype of a, and b is a supertype of b'. This is true for C# function delegates, since they're defined with the in and out keywords. You can put in and out on your own interface definitions as well, but most people don't bother (I rarely do, either).
As with all practical recursion you need base cases to stop the recursion. While you can define polymorphic functions (or classes) where input parameters and return types are themselves polymorphic, etc., these should still obey the LSP.
Postel's law as a profunctor
When viewing inputs and outputs as sets, Postel's law looks like a profunctor.
This article is part of a series titled Some design patterns as universal abstractions. Including the present article in that series is a bit of a stretch, since Postel's law isn't really a design pattern, but rather a software design principle or heuristic. I still think, however, that the article fits the spirit of the article series, if not the letter.
This article is heavily inspired by Michael Feathers' article The Universality of Postel's Law, in which he writes:
[Postel's law] has been paraphrased over the years as “Be liberal in what you accept, and conservative in what you send” and for people who are mathematically inclined: “be contravariant in your inputs and covariant in your outputs.”
A thing contravariant in input and covariant in output sounds like a profunctor, but why does Michael Feathers write that about Postel's law?
In this article, I'll try to explain.
Perfect fit #
Postel's law is a statement about functions, methods, procedures, or whatever else you'd like to call them. As I've previously outlined, with sufficient squinting, we can think about methods and other operations as functions, so in this article I'll focus on functions.
Functions don't stand alone. Functions have callers. Some other entity, usually client code, passes some input data to the function, which then performs its work and returns output data. When viewed with a set-based perspective, we can depict a function as a pipe:

Client code often use the output of one function as input for another:
Int3 isEven = EncodeEven(number); Int3 decremented = Decrement(isEven);
Even though this code example uses an explicit intermediary variable (isEven), it's equivalent to function composition:
var composition = EncodeEven.Compose(Decrement);
where Compose can be implemented as:
public static Func<A, C> Compose<A, B, C>(this Func<A, B> f, Func<B, C> g) { return x => g(f(x)); }
Such a composition we can depict by appending one pipe after another:

This works, but is brittle. It's a close fit. The output set of the first function has to exactly fit the input set of the second function. What happens if the pipes don't perfectly align?
Misalignment #
Functions compose when they fit perfectly, but in the real world, that's rarely the case. For example, it may turn out that Decrement is defined like this:
static Int3 Decrement(Int3 i) { if (i == 0) throw new ArgumentOutOfRangeException( nameof(i), "Can't decrement 0."); return i - (Int3)1; }
This function is undefined for 0. If we wanted to peek at the set diagram 'inside' the pipe, we might depict the function like this:
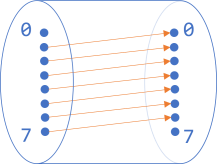
In a sense, it's still a mapping from our hypothetical 3-bit integer to 3-bit integer, but it's a partial function.
Another way to depict the mapping, however, is to constrain the domain to [1..7], and narrow the codomain to the function's image, producing a bijection:
Such sets are a little harder to express in code, because how do you represent a set with seven elements? Often, you'd stick with an implementation like the above Decrement function.
This turns out to be unfortunate, however, because EncodeEven is defined like this:
static Int3 EncodeEven(Int3 i) { return i.IsEven ? (Int3)1 : (Int3)0; }
As a set diagram, we might depict it like this:
It turns out that half the inputs into the above composition don't work! It's almost as though the pipes are misaligned:

This can easily happen, also in the real world:

This is also why Michael Feathers writes:
We can see Postel in the physical world too. Every time you see a PVC pipe with a flanged end, you’re seeing something that serves as a decent visual metaphor for Postel’s Law. Those pipes fit well together because one end is more accepting.
In other words, there's nothing new in any of the above. I've just been supplying the illustrations.
Flanges #
How should we interpret the idea of flanges? How do we illustrate them? Here's a way:
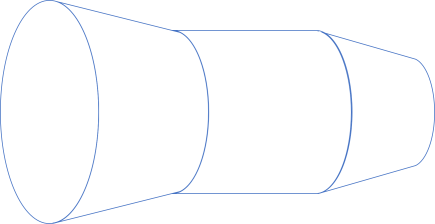
Given our set-based interpretation of things, how should we interpret a flange? Let's isolate one of them. It doesn't matter which one, but lets consider the left flange. If we attempt to make it transparent, we could also draw it like this:
What does that look like? It looks like a mapping from one set to another.
The left-hand set is slightly larger than the right-hand set, but the illustration includes neither the elements of each set nor the arrows that connect them.
If we think of the 'original' function as a function from the set A to the set B we can also write it in pseudo-code as A -> B. In Haskell you'd exactly write A -> B if A and B were two concrete types. Polymorphically, though, you'd write any function as a -> b, or in C# as Func<A, B>.
Let's think of any function a -> b as the 'perfect fit' case. While such a function composes with, say, a function b -> c, the composition is brittle. It can easily become misaligned.
How do we add flanges to the function a -> b?
As the above illustration of the flange implies, we can think of the flange as another function. Perhaps we should call the slightly larger set to the left a+ (since it's 'like' a, just larger - that is, more liberal). With that nomenclature, the flange would be a function a+ -> a.
Likewise, the right flange would be a function b -> b-. Here, I've called the narrower set of the flange b- because it's smaller (more conservative) than b.
Thus, the flanged pipe is just the composition of these three functions: a+ -> a, a -> b, and b -> b-:
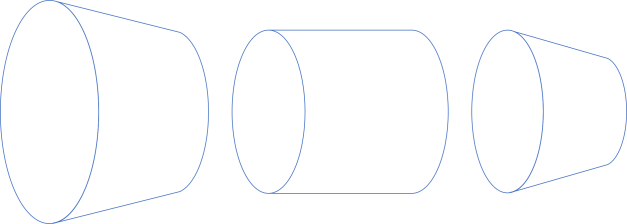
That's exactly how dimap is defined in Haskell:
dimap ab cd bc = cd . bc . ab
The implementation code uses other letters, and recall that Haskell is typically read from right to left. As its name implies, ab is a function a -> b, bc is a function b -> c, and cd is a function c -> d.
In other words, Postel's law is a description of the Reader profunctor, or, as Michael Feathers put it: Be contravariant in your inputs and covariant in your outputs.
Conclusion #
Postel's law is a useful design principle to keep in mind. Intuitively, it makes sense to think of it as making sure that pipes are flanged. The bigger the receiving flange is, and the smaller the nozzle is, the easier it is to compose the flanged pipe with other (flanged) pipes.
Using mostly visual metaphor, this article demonstrates that this is equivalent with being contravariant in input and covariant in output, and thus that the principle describes a profunctor.
Postel's law, however, isn't the only design principle describing a profunctor.

Comments
It's not "better", but here's a similar approach in Python.
from operator import contains avail = "QWERYUOPDFGHJKLZXCVBM" candidates = ((x,y,z,æ,ø) for x in avail for y in avail for z in avail for æ in "R" for ø in avail) filtered = [s for s in candidates if s[1] != "E" and s[2] != "U" and s[4] != "E" and contains(s, "E") and contains(s, "U")] for candidate in filtered[:10]: print(*candidate, sep="")