ploeh blog danish software design
Good names are skin-deep
Good names are important, but insufficient, for code maintainability.
You should give the building blocks of your code bases descriptive names. It's easier to understand the purpose of a library, module, class, method, function, etcetera if the name contains a clue about the artefact's purpose. This is hardly controversial, and while naming is hard, most teams I visit agree that names are important.
Still, despite good intentions and efforts to name things well, code bases deteriorate into unmaintainable clutter.
Clearly, good names aren't enough.
Tenuousness of names #
A good name is tenuous. First, naming is hard, so while you may have spent some effort coming up with a good name, other people may misinterpret it. Because they originate from natural language, names are as ambiguous as language. (Terse operators, on the other hand...)
Another maintainability problem with names is that implementation may change over time, but the names remain constant. Granted, modern IDEs make it easy to rename methods, but developers rarely adjust names when they adjust behaviour. Even the best names may become misleading over time.
These weakness aren't the worst, though. In my experience, a more fundamental problem is that all it takes is one badly named 'wrapper object' before the information in a good name is lost.

In the figure, the inner object is well-named. It has a clear name and descriptive method names. All it takes before this information is lost, however, is another object with vague names to 'encapsulate' it.
An attempt at a descriptive method name #
Here's an example. Imagine an online restaurant reservation system. One of the features of this system is to take reservations and save them in the database.
A restaurant, however, is a finite resource. It can only accommodate a certain number of guests at the same time. Whenever the system receives a reservation request, it'll have to retrieve the existing reservations for that time and make a decision. Can it accept the reservation? Only if it can should it save the reservation.
How do you model such an interaction? How about a descriptive name? How about TrySave? Here's a possible implementation:
public async Task<bool> TrySave(Reservation reservation) { if (reservation is null) throw new ArgumentNullException(nameof(reservation)); var reservations = await Repository .ReadReservations( reservation.At, reservation.At + SeatingDuration) .ConfigureAwait(false); var availableTables = Allocate(reservations); if (!availableTables.Any(t => reservation.Quantity <= t.Seats)) return false; await Repository.Create(reservation).ConfigureAwait(false); return true; }
There's an implicit naming convention in .NET that methods with the Try prefix indicate an operation that may or may not succeed. The return value of such methods is either true or false, and they may also have out parameters if they optionally produce a value. That's not the case here, but I think one could make the case that TrySave succinctly describes what's going on.
All is good, then?
A vague wrapper #
After our conscientious programmer meticulously designed and named the above TrySave method, it turns out that it doesn't meet all requirements. Users of the system file a bug: the system accepts reservations outside the restaurant's opening hours.
The original programmer has moved on to greener pastures, so fixing the bug falls on a poor maintenance developer with too much to do. Having recently learned about the open-closed principle, our new protagonist decides to wrap the existing TrySave in a new method:
public async Task<bool> Check(Reservation reservation) { if (reservation is null) throw new ArgumentNullException(nameof(reservation)); if (reservation.At < DateTime.Now) return false; if (reservation.At.TimeOfDay < OpensAt) return false; if (LastSeating < reservation.At.TimeOfDay) return false; return await Manager.TrySave(reservation).ConfigureAwait(false); }
This new method first checks whether the reservation is within opening hours and in the future. If that's not the case, it returns false. Only if these preconditions are fulfilled does it delegate the decision to that TrySave method.
Notice, however, the name. The bug was urgent, and our poor programmer didn't have time to think of a good name, so Check it is.
Caller's perspective #
How does this look from the perspective of calling code? Here's the Controller action that handles the pertinent HTTP request:
public async Task<ActionResult> Post(ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); Reservation? r = dto.Validate(); if (r is null) return new BadRequestResult(); var isOk = await Manager.Check(r).ConfigureAwait(false); if (!isOk) return new StatusCodeResult(StatusCodes.Status500InternalServerError); return new NoContentResult(); }
Try to forget the code you've just seen and imagine that you're looking at this code first. You'd be excused if you miss what's going on. It looks as though the method just does a bit of validation and then checks 'something' concerning the reservation.
There's no hint that the Check method might perform the significant side effect of saving the reservation in the database.
You'll only learn that if you read the implementation details of Check. As I argue in my Humane Code video, if you have to read the source code of an object, encapsulation is broken.
Such code doesn't fit in your brain. You'll struggle as you try keep track of all the things that are going on in the code, all the way from the outer boundary of the application to implementation details that relate to databases, third-party services, etcetera.
Straw man? #
You may think that this is a straw man argument. After all, wouldn't it be better to edit the original TrySave method?
Perhaps, but it would make that class more complex. The TrySave method has a cyclomatic complexity of only 3, while the Check method has a complexity of 5. Combining them might easily take them over some threshold.
Additionally, each of these two classes have different dependencies. As the TrySave method implies, it relies on both Repository and SeatingDuration, and the Allocate helper method (not shown) uses a third dependency: the restaurant's table configuration.
Likewise, the Check method relies on OpensAt and LastSeating. If you find it better to edit the original TrySave method, you'd have to combine these dependencies as well. Each time you do that, the class grows until it becomes a God object.
It's rational to attempt to separate things in multiple classes. It also, on the surface, seems to make unit testing easier. For example, here's a test that verifies that the Check method rejects reservations before the restaurant's opening time:
[Fact] public async Task RejectReservationBeforeOpeningTime() { var r = new Reservation( DateTime.Now.AddDays(10).Date.AddHours(17), "colaera@example.com", "Cole Aera", 1); var mgrTD = new Mock<IReservationsManager>(); mgrTD.Setup(mgr => mgr.TrySave(r)).ReturnsAsync(true); var sut = new RestaurantManager( TimeSpan.FromHours(18), TimeSpan.FromHours(21), mgrTD.Object); var actual = await sut.Check(r); Assert.False(actual); }
By replacing the TrySave method by a test double, you've ostensibly decoupled the Check method from all the complexity of the TrySave method.
To be clear, this style of programming, with lots of nested interfaces and tests with mocks and stubs is far from ideal, but I still find it better than a big ball of mud.
Alternative #
A better alternative is Functional Core, Imperative Shell, AKA impureim sandwich. Move all impure actions to the edge of the system, leaving only referentially transparent functions as the main implementers of logic. It could look like this:
[HttpPost] public async Task<ActionResult> Post(ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); var id = dto.ParseId() ?? Guid.NewGuid(); Reservation? r = dto.Validate(id); if (r is null) return new BadRequestResult(); var reservations = await Repository.ReadReservations(r.At).ConfigureAwait(false); if (!MaitreD.WillAccept(DateTime.Now, reservations, r)) return NoTables500InternalServerError(); await Repository.Create(r).ConfigureAwait(false); return Reservation201Created(r); }
Nothing is swept under the rug here. WillAccept is a pure function, and while it encapsulates significant complexity, the only thing you need to understand when you're trying to understand the above Post code is that it returns either true or false.
Another advantage of pure functions is that they are intrinsically testable. That makes unit testing and test-driven development easier.
Even with a functional core, you'll also have an imperative shell. You can still test that, too, such as the Post method. It isn't referentially transparent, so you might be inclined to use mocks and stubs, but I instead recommend state-based testing with a Fake database.
Conclusion #
Good names are important, but don't let good names, alone, lull you into a false sense of security. All it takes is one vaguely named wrapper object, and all the information in your meticulously named methods is lost.
This is one of many reasons I try to design with static types instead of names. Not that I dismiss the value of good names. After all, you'll have to give your types good names as well.
Types are more robust in the face of inadvertent changes; or, rather, they tend to resist when we try to do something stupid. I suppose that's what lovers of dynamically typed languages feel as 'friction'. In my mind, it's entirely opposite. Types keep me honest.
Unfortunately, most type systems don't offer an adequate degree of safety. Even in F#, which has a great type system, you can introduce impure actions into what you thought was a pure function, and you'd be none the wiser. That's one of the reasons I find Haskell so interesting. Because of the way IO works, you can't inadvertently sweep surprises under the rug.
Redirect legacy URLs
Evolving REST API URLs when cool URIs don't change.
More than one reader reacted to my article on fit URLs by asking about bookmarks and original URLs. Daniel Sklenitzka's question is a good example:
While I answered the question on the same page, I think that it's worthwhile to expand it."I see how signing the URLs prevents clients from retro-engineering the URL templates, but how does it help preventing breaking changes? If the client stores the whole URL instead of just the ID and later the URL changes because a restaurant ID is added, the original URL is still broken, isn't it?"
The rules of HTTP #
I agree with the implicit assumption that clients are allowed to bookmark links. It seems, then, like a breaking change if you later change your internal URL scheme. That seems to imply that the bookmarked URL is gone, breaking a tenet of the HTTP protocol: Cool URIs don't change.
REST APIs are supposed to play by the rules of HTTP, so it'd seem that once you've published a URL, you can never retire it. You can, on the other hand, change its behaviour.
Let's call such URLs legacy URLs. Keep them around, but change them to return 301 Moved Permanently responses.
The rules of REST go both ways. The API is expected to play by the rules of HTTP, and so are the clients. Clients are not only expected to follow links, but also redirects. If a legacy URL starts returning a 301 Moved Permanently response, a well-behaved client doesn't break.
Reverse proxy #
As I've previously described, one of the many benefits of HTTP-based services is that you can put a reverse proxy in front of your application servers. I've no idea how to configure or operate NGINX or Varnish, but from talking to people who do know, I get the impression that they're quite scriptable.
Since the above ideas are independent of actual service implementation or behaviour, it's a generic problem that you should seek to address with general-purpose software.
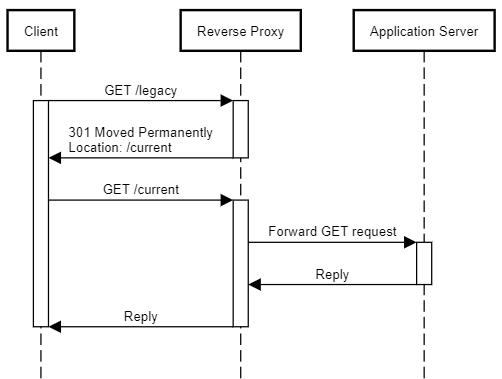
Imagine that a reverse proxy is configured with a set of rules that detects legacy URLs and knows how to forward them. Clearly, the reverse proxy must know of the REST API's current URL scheme to be able to do that. You might think that this would entail leaking an implementation detail, but just as I consider any database used by the API as part of the overall system, I'd consider the reverse proxy as just another part.
Redirecting with ASP.NET #
If you don't have a reverse proxy, you can also implement redirects in code. It'd be better to use something like a reverse proxy, because that would mean that you get to delete code from your code base, but sometimes that's not possible.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
In ASP.NET, you can return 301 Moved Permanently responses just like any other kind of HTTP response:
[Obsolete("Use Get method with restaurant ID.")] [HttpGet("calendar/{year}/{month}")] public ActionResult LegacyGet(int year, int month) { return new RedirectToActionResult( nameof(Get), null, new { restaurantId = Grandfather.Id, year, month }, permanent: true); }
This LegacyGet method redirects to the current Controller action called Get by supplying the arguments that the new method requires. The Get method has this signature:
[HttpGet("restaurants/{restaurantId}/calendar/{year}/{month}")] public async Task<ActionResult> Get(int restaurantId, int year, int month)
When I expanded the API from a single restaurant to a multi-tenant system, I had to grandfather in the original restaurant. I gave it a restaurantId, but in order to not put magic constants in the code, I defined it as the named constant Grandfather.Id.
Notice that I also adorned the LegacyGet method with an [Obsolete] attribute to make it clear to maintenance programmers that this is legacy code. You might argue that the Legacy prefix already does that, but the [Obsolete] attribute will make the compiler emit a warning, which is even better feedback.
Regression test #
While legacy URLs may be just that: legacy, that doesn't mean that it doesn't matter whether or not they work. You may want to add regression tests.
If you implement redirects in code (as opposed to a reverse proxy), you should also add automated tests that verify that the redirects work:
[Theory] [InlineData("http://localhost/calendar/2020?sig=ePBoUg5gDw2RKMVWz8KIVzF%2Fgq74RL6ynECiPpDwVks%3D")] [InlineData("http://localhost/calendar/2020/9?sig=ZgxaZqg5ubDp0Z7IUx4dkqTzS%2Fyjv6veDUc2swdysDU%3D")] public async Task BookmarksStillWork(string bookmarkedAddress) { using var api = new LegacyApi(); var actual = await api.CreateDefaultClient().GetAsync(new Uri(bookmarkedAddress)); Assert.Equal(HttpStatusCode.MovedPermanently, actual.StatusCode); var follow = await api.CreateClient().GetAsync(actual.Headers.Location); follow.EnsureSuccessStatusCode(); }
This test interacts with a self-hosted service at the HTTP level. LegacyApi is a test-specific helper class that derives from WebApplicationFactory<Startup>.
The test uses URLs that I 'bookmarked' before I evolved the URLs to a multi-tenant system. As you can tell from the host name (localhost), these are bookmarks against the self-hosted service. The test first verifies that the response is 301 Moved Permanently. It then requests the new address and uses EnsureSuccessStatusCode as an assertion.
Conclusion #
When you evolve fit URLs, it could break clients that may have bookmarked legacy URLs. Consider leaving 301 Moved Permanently responses at those addresses.
Checking signed URLs with ASP.NET
Use a filter to check all requested URL signatures.
This article is part of a short series on fit URLs. In the overview article, I argued that you should be signing URLs in order to prevent your REST APIs from becoming victims of Hyrum's law. In the previous article you saw how to sign URLs with ASP.NET.
In this article you'll see how to check the URLs of all HTTP requests to the API and reject those that aren't up to snuff.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
Filter #
If you want to intercept all incoming HTTP requests in ASP.NET Core, an IAsyncActionFilter is a good option. This one should look at the URL of all incoming HTTP requests and detect if the client tried to tamper with it.
internal sealed class UrlIntegrityFilter : IAsyncActionFilter { private readonly byte[] urlSigningKey; public UrlIntegrityFilter(byte[] urlSigningKey) { this.urlSigningKey = urlSigningKey; } // More code comes here...
The interface only defines a single method:
public async Task OnActionExecutionAsync( ActionExecutingContext context, ActionExecutionDelegate next) { if (IsGetHomeRequest(context)) { await next().ConfigureAwait(false); return; } var strippedUrl = GetUrlWithoutSignature(context); if (SignatureIsValid(strippedUrl, context)) { await next().ConfigureAwait(false); return; } context.Result = new NotFoundResult(); }
While the rule is to reject requests with invalid signatures, there's one exception. The 'home' resource requires no signature, as this is the only publicly documented URL for the API. Thus, if IsGetHomeRequest returns true, the filter invokes the next delegate and returns.
Otherwise, it strips the signature off the URL and checks if the signature is valid. If it is, it again invokes the next delegate and returns.
If the signature is invalid, on the other hand, the filter stops further execution by not invoking next. Instead, it sets the response to a 404 Not Found result.
It may seem odd to return 404 Not Found if the signature is invalid. Wouldn't 401 Unauthorized or 403 Forbidden be more appropriate?
Not really. Keep in mind that while this behaviour may use encryption technology, it's not a security feature. The purpose is to make it impossible for clients to 'retro-engineer' an implied interface. This protects them from breaking changes in the future. Clients are supposed to follow links, and the URLs given by the API itself are proper, existing URLs. If you try to edit a URL, then that URL doesn't work. It represents a resource that doesn't exist. While it may seem surprising at first, I find that a 404 Not Found result is the most appropriate status code to return.
Detecting a home request #
The IsGetHomeRequest helper method is straightforward:
private static bool IsGetHomeRequest(ActionExecutingContext context) { return context.HttpContext.Request.Path == "/" && context.HttpContext.Request.Method == "GET"; }
This predicate only looks at the Path and Method of the incoming request. Perhaps it also ought to check that the URL has no query string parameters, but I'm not sure if that actually matters.
Stripping off the signature #
The GetUrlWithoutSignature method strips off the signature query string variable from the URL, but leaves everything else intact:
private static string GetUrlWithoutSignature(ActionExecutingContext context) { var restOfQuery = QueryString.Create( context.HttpContext.Request.Query.Where(x => x.Key != "sig")); var url = context.HttpContext.Request.GetEncodedUrl(); var ub = new UriBuilder(url); ub.Query = restOfQuery.ToString(); return ub.Uri.AbsoluteUri; }
The purpose of removing only the sig query string parameter is that it restores the rest of the URL to the value that it had when it was signed. This enables the SignatureIsValid method to recalculate the HMAC.
Validating the signature #
The SignatureIsValid method validates the signature:
private bool SignatureIsValid(string candidate, ActionExecutingContext context) { var sig = context.HttpContext.Request.Query["sig"]; var receivedSignature = Convert.FromBase64String(sig.ToString()); using var hmac = new HMACSHA256(urlSigningKey); var computedSignature = hmac.ComputeHash(Encoding.ASCII.GetBytes(candidate)); var signaturesMatch = computedSignature.SequenceEqual(receivedSignature); return signaturesMatch; }
If the receivedSignature equals the computedSignature the signature is valid.
This prevents clients from creating URLs based on implied templates. Since clients don't have the signing key, they can't compute a valid HMAC, and therefore the URLs they'll produce will fail the integrity test.
Configuration #
As is the case for the URL-signing feature, you'll first need to read the signing key from the configuration system. This is the same key used to sign URLs:
var urlSigningKey = Encoding.ASCII.GetBytes( Configuration.GetValue<string>("UrlSigningKey"));
Next, you'll need to register the filter with the ASP.NET framework:
services.AddControllers(opts => opts.Filters.Add(new UrlIntegrityFilter(urlSigningKey)));
This is typically done in the ConfigureServices method of the Startup class.
Conclusion #
With a filter like UrlIntegrityFilter you can check the integrity of URLs on all incoming requests to your REST API. This prevents clients from making up URLs based on an implied interface. This may seem restrictive, but is actually for their own benefit. When they can't assemble URLs from scratch, the only remaining option is to follow the links that the API provides.
This enables you to evolve the API without breaking existing clients. While client developers may not initially appreciate having to follow links instead of building URLs out of templates, they may value that their clients don't break as you evolve the API.
Next: Redirect legacy URLs.
Signing URLs with ASP.NET
A few Decorators is all it takes.
This article is part of a short series on fit URLs. In the overview article, I argued that you should be signing URLs in order to prevent your REST APIs from becoming victims of Hyrum's law.
In this article, you'll see how to do this with ASP.NET Core 3.1, and in the next article you'll see how to check URL integrity.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
SigningUrlHelper #
I wanted the URL-signing functionality to slot into the ASP.NET framework, which supplies the IUrlHelper interface for the purpose of creating URLs. (For example, the UrlBuilder I recently described relies on that interface.)
Since it's an interface, you can define a Decorator around it:
internal sealed class SigningUrlHelper : IUrlHelper { private readonly IUrlHelper inner; private readonly byte[] urlSigningKey; public SigningUrlHelper(IUrlHelper inner, byte[] urlSigningKey) { this.inner = inner; this.urlSigningKey = urlSigningKey; } // More code comes here...
As you can tell, this Decorator requires an inner IUrlHelper and a urlSigningKey. Most of the members just delegate to the inner implementation:
public bool IsLocalUrl(string url) { return inner.IsLocalUrl(url); }
The Action method creates URLs, so this is the method to modify:
public string Action(UrlActionContext actionContext) { var url = inner.Action(actionContext); if (IsLocalUrl(url)) { var b = new UriBuilder( ActionContext.HttpContext.Request.Scheme, ActionContext.HttpContext.Request.Host.ToUriComponent()); url = new Uri(b.Uri, url).AbsoluteUri; } var ub = new UriBuilder(url); using var hmac = new HMACSHA256(urlSigningKey); var sig = Convert.ToBase64String( hmac.ComputeHash(Encoding.ASCII.GetBytes(url))); ub.Query = new QueryString(ub.Query).Add("sig", sig).ToString(); return ub.ToString(); }
The actionContext may sometimes indicate a local (relative) URL, in which case I wanted to convert it to an absolute URL. Once that's taken care of, the method calculates an HMAC and adds it as a query string variable.
SigningUrlHelperFactory #
While it's possible take ASP.NET's default IUrlHelper instance (e.g. from ControllerBase.Url) and manually decorate it with SigningUrlHelper, that doesn't slot seamlessly into the framework.
For example, to add the Location header that you saw in the previous article, the code is this:
private static ActionResult Reservation201Created( int restaurantId, Reservation r) { return new CreatedAtActionResult( nameof(Get), null, new { restaurantId, id = r.Id.ToString("N") }, r.ToDto()); }
The method just returns a new CreatedAtActionResult object, and the framework takes care of the rest. No explicit IUrlHelper object is used, so there's nothing to manually decorate. By default, then, the URLs created from such CreatedAtActionResult objects aren't signed.
It turns out that the ASP.NET framework uses an interface called IUrlHelperFactory to create IUrlHelper objects. Decorate that as well:
public sealed class SigningUrlHelperFactory : IUrlHelperFactory { private readonly IUrlHelperFactory inner; private readonly byte[] urlSigningKey; public SigningUrlHelperFactory(IUrlHelperFactory inner, byte[] urlSigningKey) { this.inner = inner; this.urlSigningKey = urlSigningKey; } public IUrlHelper GetUrlHelper(ActionContext context) { var url = inner.GetUrlHelper(context); return new SigningUrlHelper(url, urlSigningKey); } }
Straightforward: use the inner object to get an IUrlHelper object, and decorate it with SigningUrlHelper.
Configuration #
The final piece of the puzzle is to tell the framework about the SigningUrlHelperFactory. You can do this in the Startup class' ConfigureServices method.
First, read the signing key from the configuration system (e.g. a configuration file):
var urlSigningKey = Encoding.ASCII.GetBytes( Configuration.GetValue<string>("UrlSigningKey"));
Then use the signing key to configure the SigningUrlHelperFactory service. Here, I wrapped that in a little helper method:
private static void ConfigureUrSigning( IServiceCollection services, byte[] urlSigningKey) { services.RemoveAll<IUrlHelperFactory>(); services.AddSingleton<IUrlHelperFactory>( new SigningUrlHelperFactory( new UrlHelperFactory(), urlSigningKey)); }
This method first removes the default IUrlHelperFactory service and then adds the SigningUrlHelperFactory instead. It decorates UrlHelperFactory, which is the default built-in implementation of the interface.
Conclusion #
You can extend the ASP.NET framework to add a signature to all the URLs it generates. All it takes is two simple Decorators.
Fit URLs
Keep REST API URLs evolvable. A way to address Hyrum's law.
Publishing and maintaining a true (level 3) RESTful API is difficult. This is the style of REST design where clients are expected to follow links to perform the work they want to accomplish; not assemble URLs from templates.
Have you ever designed a URL scheme and published it, only to later discover that you wished you'd come up with a different structure? If you've published a set of URL templates, changing your mind constitutes a breaking change. If clients follow links, however, URLs are opaque and you can redesign the URLs without breaking existing clients.
You can try to document this design principle all you want, to no avail. You can tell client developers that they're supposed to follow links, not try to retro-engineer the URLs, and still they'll do it.
I know; I've experienced it. When we later changed the URL structure, it didn't take long for the client developers to complain that we broke their code.
Hyrum's law #
This is an example of Hyrum's law in action, albeit on the scale of web service interactions, rather than low-level APIs. The presence of a discernible system to URLs suggests an implicit interface.
Consider this 'home' resource for an online restaurant reservation system:
GET / HTTP/1.1
HTTP/1.1 200 OK
Content-Type: application/json; charset=utf-8
{
"links": [
{
"rel": "urn:reservations",
"href": "http://localhost:53568/reservations"
},
{
"rel": "urn:year",
"href": "http://localhost:53568/calendar/2020"
},
{
"rel": "urn:month",
"href": "http://localhost:53568/calendar/2020/10"
},
{
"rel": "urn:day",
"href": "http://localhost:53568/calendar/2020/10/23"
}
]
}
It doesn't take much interaction with the API before you realise that there's a system to the URLs provided in the links. If you want to see the calendar for a specific date, you can easily retro-engineer the URL template /calendar/{yyyy}/{MM}/{dd}, and /calendar/{yyyy}/{MM} for a month, and so on.
The same is likely to happen with the reservations link. You can POST to this link to make a new reservation:
POST /reservations HTTP/1.1
Content-Type: application/json
{
"at": "2020-12-09 19:15",
"email": "rainboughs@example.com",
"name": "Raine Burroughs",
"quantity": 5
}
HTTP/1.1 201 Created
Content-Type: application/json
Location: http://localhost:53568/reservations/fabc5bf63a1a4db38b95deaa89c01178
{
"id": "fabc5bf63a1a4db38b95deaa89c01178",
"at": "2020-12-09T19:15:00.0000000",
"email": "rainboughs@example.com",
"name": "Raine Burroughs",
"quantity": 5
}
Notice that when the API responds, its Location header gives you the URL for that particular reservation. It doesn't take long to figure out that there's a template there, as well: /reservations/{id}.
So client developers may just store the ID (fabc5bf63a1a4db38b95deaa89c01178) and use the implied template to construct URLs on the fly. And who can blame them?
That, however, misses the point of REST. The ID of that reservation isn't fabc5bf63a1a4db38b95deaa89c01178, but rather http://localhost:53568/reservations/fabc5bf63a1a4db38b95deaa89c01178. Yes, the URL, all of it, is the ID.
Evolving URLs #
Why does that matter?
It matters because you're human, and you make mistakes. Or, rather, it's intrinsic to software development that you learn as you work. You'll make decisions at the beginning that you'll want to change as you gain more insight.
Also, requirements change. Consider the URL template scheme implied by the above examples. Can you spot any problems? Would you want to change anything?
Imagine, for example, that you've already deployed the first version of the API. It's a big success. Now the product owner wants to expand the market to more restaurants. She wants to make the service a multi-tenant API. How does that affect URLs?
In that new context, perhaps URLs like /restaurants/1/reservations or /restaurants/90125/calendar/2020/10 would be better.
That, however, would be a breaking change if clients construct URLs based on implied templates.
Couldn't you just pass the restaurant ID as an HTTP header instead of in the URL? Yes, technically you could do that, but that doesn't work well with HTTP caching. It's not a RESTful thing to do, for that, and other, reasons.
Fitness #
Do we just give up in the face of Hyrum's law? Or can we keep URLs evolvable? In evolution, organisms evolve according to a 'fitness function', so to name such URLs, we could call them fit URL.
To keep URLs fit, we must prevent client developers from retro-engineering the implied interface. My original thought was to give each URL an opaque ID, such as a GUID, but in 2015 Dan Kubb instead suggested to sign the URLs. What a great idea!
If you do that, then the above home resource might look like this:
{
"links": [
{
"rel": "urn:reservations",
"href": "http://localhost:53568/restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D"
},
{
"rel": "urn:year",
"href": "http://localhost:53568/restaurants/1/calendar/2020?sig=eIFuUkb6WprPrp%2B4HPSPaavcUdwVjeG%2BKVrIRqDs9OI%3D"
},
{
"rel": "urn:month",
"href": "http://localhost:53568/restaurants/1/calendar/2020/10?sig=mGqkAjY7vMbC5Fr7UiRXWWnjn3pFn21MYrMagpdWaU0%3D"
},
{
"rel": "urn:day",
"href": "http://localhost:53568/restaurants/1/calendar/2020/10/23?sig=Ua5F%2FucP6zmAy219cHa4WG7zIcCa0hgVD5ModXcNQuo%3D"
}
]
}
Even if you can still figure out what the URL templates are, it doesn't avail you. Creating a new reservation may return a URL like https://localhost:53568/restaurants/1/reservations/fabc5bf63a1a4db38b95deaa89c01178?sig=8e80PmVi8aSS1UH6iSJ73nHmOsCLrUMs7yggEOkvEqo%3D, but you can't just replace the ID with another ID and expect it to work:
GET /restaurants/1/reservations/79520877ef4f4acdb69838e22ad04510?sig=8e80PmVi8aSS1UH6iSJ73nHmOsCLrUMs7yggEOkvEqo%3D HTTP/1.1 HTTP/1.1 404 Not Found
You're requesting a URL that doesn't exist, so the result is 404 Not Found. To be clear: yes, there is a reservation with the ID 79520877ef4f4acdb69838e22ad04510, but its URL isn't the above URL.
ASP.NET implementation #
In two articles, I'll show you how to implement fit URLs in ASP.NET Core.
The ASP.NET framework comes with enough extensibility points to make this a non-intrusive operation. I implemented this using a filter and a few Decorators in a way so that you can easily turn the feature on or off.Conclusion #
One of the major benefits of true RESTful API design is that it's evolvable. It enables you to learn and improve as you go, without breaking existing clients.
You have to take care, however, that clients don't retro-engineer the URL templates that you may be using for implementation purposes. You want to be able to change URLs in the future.
Hyrum's law suggests that clients will rely on undocumented features if they can. By signing the URLs you keep them fit to evolve.
Next: Signing URLs with ASP.NET.
Comments
I see how signing the URLs prevents clients from retro-engineering the URL templates, but how does it help preventing breaking changes? If the client stores the whole URL instead of just the ID and later the URL changes because a restaurant ID is added, the original URL is still broken, isn't it?
Daniel, thank you for writing. You're correct when assuming that clients are allowed to 'bookmark' URLs. An implicit assumption that I didn't explicitly state is that clients are supposed to follow not only links, but also redirects. Thus, to avoid breaking changes, it's the API's responsibility to leave a 301 Moved Permanently response behind at the old address.
As a service owner, though, you have some flexibility in how to achieve this. You can code this into the service code itself, but another option might be to use a reverse proxy for such purposes. One of the many advantages of REST is that you can offload a lot HTTP-level behaviour on standard networking software; here's another example.
I think I have the same confusion as Daniel.
If you've published a set of URL templates, changing your mind constitutes a breaking change. If clients follow links, however, URLs are opaque and you can redesign the URLs without breaking existing clients.
...
You're correct when assuming that clients are allowed to 'bookmark' URLs. An implicit assumption that I didn't explicitly state is that clients are supposed to follow not only links, but also redirects. Thus, to avoid breaking changes, it's the API's responsibility to leave a
301 Moved Permanentlyresponse behind at the old address.
Is there a certain kind of breaking change that exists for a level 2 API that doesn't exist for a level 3 API?
Tyson, thank you for writing. I haven't thought much about whether there are categories of errors that differ between the levels, but I think that in practice, there's a difference in mindset.
With a level 2 API, I think most people are still caught in a mindset that's largely a projection of RPC. URL templates map easily to programming procedures (e.g. object-oriented methods). Thus, you have a mental model that includes PostReservation, GetCalendar, etc. People think of that as being the API. With that mindset, I don't think that many client developers configure their HTTP clients to follow redirects. Thus, one could argue that changing URLs are breaking changes for a level 2 API, even if you leave 301 Moved Permanently responses behind.
With level 3 APIs, you encourage client developers to think in terms of 'the web'. That includes following links and redirects. I believe that there's a difference in perception, even if there may not be any technical difference.
I do believe, however, that the real advantage is that you impose a smaller maintenance burden on client developers with a level 3 API. Granted, a client developer may have to spend a little more effort up front to follow links, but once a compliant client is in place, it needs no more maintenance. It'll just keep working.
Not so with published URL templates. Here you have to entice client developers to actively update their code. This may be impossible if you don't know who the clients are, or if the client software is in maintenance mode. This may make it harder to retire old versions. You may be stuck with these old versions forever.
Monomorphic functors
Non-generic mappable containers, with a realistic example.
This article is an instalment in an article series about functors. Previous articles have covered Maybe, Lazy, and other functors. This article looks at what happens when you weaken one of the conditions that the article series so far has implied.
In the introductory article, I wrote:
As a rule of thumb, if you have a type with a generic type argument, it's a candidate to be a functor.That still holds, but then Tyson Williams asks if that's a required condition. It turns out that it isn't. In this article, you'll learn about the implications of weakening this condition.
As is my habit with many of the articles in this article series, I'll start by uncovering the structure of the concept, and only later show a more realistic example.
Mapping strings #
So far in this article series, you've seen examples of containers with a generic type argument: Tree<T>, Task<T>, and so on. Furthermore, you've seen how a functor is a container with a structure-preserving map. This function has various names in different languages: Select, fmap, map, etcetera.
Until now, you've only seen examples where this mapping enables you to translate from one type argument to another. You can, for example, translate the characters in a string to Boolean values, like this:
> "Safe From Harm".Select(c => c.IsVowel()) Enumerable.WhereSelectEnumerableIterator<char, bool> { false, true, false, true, false, false, false, true, false, false, false, true, false, false }
This works because in C#, the String class implements various interfaces, among these IEnumerable<char>. By treating a string as an IEnumerable<char>, you can map each element. That's the standard IEnumerable functor (AKA the list functor).
What if you'd like to map the characters in a string to other characters? Perhaps you'd like to map vowels to upper case, and all other characters to lower case. You could try this:
> "Safe From Harm".Select(c => c.IsVowel() ? char.ToUpper(c) : char.ToLower(c)) Enumerable.WhereSelectEnumerableIterator<char, char> { 's', 'A', 'f', 'E', ' ', 'f', 'r', 'O', 'm', ' ', 'h', 'A', 'r', 'm' }
That sort of works, but as you can tell, the result isn't a string, it's an IEnumerable<char>.
This isn't a big problem, because one of the string constructor overloads take a char array as input, so you can do this:
> new string ("Safe From Harm".Select(c => c.IsVowel() ? char.ToUpper(c) : char.ToLower(c)).ToArray()) "sAfE frOm hArm"
It isn't the prettiest, but it gets the job done.
Monomorphic functor in C# #
If you contemplate the last example, you may arrive at the conclusion that you could package some of that boilerplate code in a reusable function. Since we're already talking about functors, why not call it Select?
public static string Select(this string source, Func<char, char> selector) { return new string(source.AsEnumerable().Select(selector).ToArray()); }
It somewhat simplifies things:
> "Safe From Harm".Select(c => c.IsVowel() ? char.ToUpper(c) : char.ToLower(c)) "sAfE frOm hArm"
Since I deliberately wrote the Select method in the style of other Select methods (apart from the generics), you may wonder if C# query syntax also works?
> from c in "Army of Me" . select c.IsVowel() ? char.ToUpper(c) : char.ToLower(c) "ArmY Of mE"
It compiles and works! The C# compiler understands monomorphic containers!
I admit that I was quite surprised when I first tried this out.
Monomorphic functor in Haskell #
Surprisingly, in this particular instance, C# comes out looking more flexible than Haskell. This is mainly because in C#, functors are implemented as a special compiler feature, whereas in Haskell, Functor is defined using the general-purpose type class language feature.
There's a package that defines a MonoFunctor type class, as well as some instances. With it, you can write code like this:
ftg :: Text ftg = omap (\c -> if isVowel c then toUpper c else toLower c) "Fade to Grey"
Even though Text isn't a Functor instance, it is a MonoFunctor instance. The value of ftg is "fAdE tO grEY".
All the normal functors ([], Maybe, etc.) are also MonoFunctor instances, since the normal Functor instance is more capable than a MonoFunctor.
Restaurant example #
While I've introduced the concept of a monomorphic functor with a trivial string example, I actually discovered the C# feature when I was working on some more realistic code. As I often do, I was working on a variation of an online restaurant reservation system. The code shown in the following is part of the sample code base that accompanies my book Code That Fits in Your Head.
The code base contained a rather complex variation of an implementation of the Maître d' kata. The MaitreD constructor looked like this:
public MaitreD( TimeOfDay opensAt, TimeOfDay lastSeating, TimeSpan seatingDuration, IEnumerable<Table> tables)
This had worked well when the system only dealt with a single restaurant, but I was now expanding it to a multi-tenant system and I needed to keep track of some more information about each restaurant, such as its name and ID. While I could have added such information to the MaitreD class, I didn't want to pollute that class with data it didn't need. While the restaurant's opening time and seating duration are necessary for the decision algorithm, the name isn't.
So I introduced a wrapper class:
public sealed class Restaurant { public Restaurant(int id, string name, MaitreD maitreD) { Id = id; Name = name; MaitreD = maitreD; } public int Id { get; } public string Name { get; } public MaitreD MaitreD { get; } // More code follows...
I also added copy-and-update methods (AKA 'withers'):
public Restaurant WithId(int newId) { return new Restaurant(newId, Name, MaitreD); } public Restaurant WithName(string newName) { return new Restaurant(Id, newName, MaitreD); } public Restaurant WithMaitreD(MaitreD newMaitreD) { return new Restaurant(Id, Name, newMaitreD); }
Still, if you need to modify the MaitreD within a given Restaurant object, you first have to have a reference to the Restaurant so that you can read its MaitreD property, then you can edit the MaitreD, and finally call WithMaitreD. Doable, but awkward:
restaurant.WithMaitreD(restaurant.MaitreD.WithSeatingDuration(TimeSpan.FromHours(.5)))
So I got the idea that I might try to add a structure-preserving map to Restaurant, which I did:
public Restaurant Select(Func<MaitreD, MaitreD> selector) { if (selector is null) throw new ArgumentNullException(nameof(selector)); return WithMaitreD(selector(MaitreD)); }
The first time around, it enabled me to rewrite the above expression as:
restaurant.Select(m => m.WithSeatingDuration(TimeSpan.FromHours(.5)))
That's already a little nicer. It also handles the situation where you may not have a named Restaurant variable you can query; e.g. if you have a method that returns a Restaurant object, and you just want to continue calling into a Fluent API.
Then I thought, I wonder if query syntax works, too...
from m in restaurant select m.WithSeatingDuration(TimeSpan.FromHours(.5))
And it does work!
I know that a lot of people don't like query syntax, but I think it has certain advantages. In this case, it actually isn't shorter, but it's a nice alternative. I particularly find that if I try to fit my code into a tight box, query syntax sometimes gives me an opportunity to format code over multiple lines in a way that's more natural than with method-call syntax.
Conclusion #
A monomorphic functor is still a functor, only it constrains the type of mapping you can perform. It can be useful to map monomorphic containers like strings, or immutable nested data structures like the above Restaurant class.
Next: Set is not a functor.
Comments
Excellent article! I was planning to eventually write a blog post on this topic, but now there is no need.
I know that a lot of people don't like query syntax, but I think it has certain advantages. In this case, it actually isn't shorter, but it's a nice alternative. I particularly find that if I try to fit my code into a tight box, query syntax sometimes gives me an opportunity to format code over multiple lines in a way that's more natural than with method-call syntax.
Said another way, one objective measure that is better in this case when using query syntax is that the maximum line width is smaller. It is objective primarily in the sense that maximum line width is objective and secondarily in the sense that we generally agree that code with a lower maximum line width is typically easier to understand.
Another such objective measure of quality that I value is the maximum number of matching pairs of parentheses that are nested. This measure improves to two in your query syntax code from three in your previous code. The reason it was three before is because there are four levels of detail and your code decreases the level of detail three times: Restaurant to MaitreD, MaitreD to TimeSpan, and TimeSpan to double. Query syntax is one way to decrease the level of detail without having to introduce a pair of matching parentheses.
I find more success minimizing this measure of quality when taking a bottom-up approach. Using the Apply extension method from language-ext, which is like the forward pipe operator in F#, we can rewrite this code without any nested pairs of matching parentheses as
.5.Apply(TimeSpan.FromHours).Apply(m => m.WithSeatingDuration).Apply(restaurant.Select)
(I did not check if this code compiles. If it does not, it would be because the C# compiler is unsure how to implicitly convert some method group to its intended Func<,> delegate.) This code also has natural line-breaking points before each dot operator, which leads to a comfortable value for the maximum line width.
Another advantage of this code that I value is that the execution happens in the same order in which I (as an English speaker) read it: left to right. Your code before using the query syntax executed from right to left as dictated by the matching parentheses. In fact, since the dot operator is left associative, the degree to which execution occurs from left to right is inversely correlated to the number of nested pairs of parentheses. (One confusing thing here is the myriad of different semantic meanings in C# to the syntactic use of a pair of parentheses.)
Tyson, thank you for writing. I've never thought about measuring complexity by nested parentheses, but I like it! It makes intuitive sense.
I'm not sure it applies to LISP-like languages, but perhaps some reader comes by some day who can enlighten us.
While reading your articles about contravairant functors, a better name occured to me for what you called a monomorphic functor in this article.
For a covariant functor, its mapping function accepts a function with types that vary (i.e. differ). The order in which they vary matches the order that the types vary in the corresponding elevated function. For a contravariant functor, its mapping function also accepts a function with types that vary. However, the order in which they vary is reversed compared to the order that the types vary in the corresponding elevated function. For the functor in this article that you called a monomorphic functor, its mapping function accepts a function with types that do not vary. As such, we should call such a functor an invariant functor.
Tyson, thank you for writing. That's a great suggestion that makes a lot of sense.
The term invariant functor seems, however, to be taken by a wider definition.
"an invariant type
Tallows you to map fromatobif and only ifaandbare isomorphic. In a very real sense, this isn't an interesting property - an isomorphism betweenaandbmeans that they're already the same thing to begin with."
This seems, at first glance, to fit your description quite well, but when we try to encode this in a programming language, something surprising happens. We'd typically say that the types a and b are isomorphic if and only if there exists two functions a -> b and b -> a. Thus, we can encode this in a Haskell type class like this one:
class Invariant f where invmap :: (a -> b) -> (b -> a) -> f a -> f b
I've taken the name of both type class and method from Thinking with Types, but we find the same naming in Data.Functor.Invariant. The first version of the invariant package is from 2012, so assume that Sandy Maguire has taken the name from there (and not the other way around).
There's a similar-looking definition in Cats (although I generally don't read Scala), and in C# we might define a method like this:
public sealed class Invariant<A> { public Invariant<B> InvMap<B>(Func<A, B> selector1, Func<B, A> selector2) }
This seems, at first glance, to describe monomorphic functors quite well, but it turns out that it's not quite the same. Consider mapping of String, as discussed in this article. The MonoFunctor instance of String (or, generally, [a]) lifts a Char -> Char function to String -> String.
In Haskell, String is really a type alias for [Char], but what happens if we attempt to describe String as an Invariant instance? We can't, because String has no type argument.
We can, however, see what happens if we try to make [a] an Invariant instance. If we can do that, we can try to experiment with Char's underlying implementation as a number:
"To convert a
Charto or from the correspondingIntvalue defined by Unicode, usetoEnumandfromEnumfrom theEnumclass respectively (or equivalentlyordandchr)."
ord and chr enable us to treat Char and Int as isomorphic:
> ord 'h' 104 > chr 104 'h'
Since we have both Char -> Int and Int -> Char, we should be able to use invmap ord chr, and indeed, it works:
> invmap ord chr "foo" [102,111,111]
When, however, we look at the Invariant [] instance, we may be in for a surprise:
instance Invariant [] where invmap f _ = fmap f
The instance uses only the a -> b function, while it completely ignores the b -> a function! Since the instance uses fmap, rather than map, it also strongly suggests that all (covariant) Functor instances are also Invariant instances. That's also the conclusion reached by the invariant package. Not only that, but every Contravariant functor is also an Invariant functor.
That seems to completely counter the idea that a and b should be isomorphic. I can't say that I've entirely grokked this disconnect yet, but it seems to me to be an artefact of instances' ability to ignore either of the functions passed to invmap. At least we can say that client code can't call invmap unless it supplies both functions (here I pretend that undefined doesn't exist).
If we go with the Haskell definition of things, an invariant functor is a much wider concept than a monomorphic functor. Invariant describes a superset that contains both (covariant) Functor and Contravariant functor. This superset is more than just the union of those two sets, since it also includes containers that are neither Functor nor Contravariant, for example Endo:
instance Invariant Endo where invmap f g (Endo h) = Endo (f . h . g)
For example, toUpper is an endomorphism, so we can apply it to invmap and evaluate it like this:
> (appEndo $ invmap ord chr $ Endo toUpper) 102 70
This example takes the Int 102 and converts it to a String with chr:
> chr 102 'f'
It then applies 'f' to toUpper:
> toUpper 'f' 'F'
Finally, it converts 'F' with ord:
> ord 'F' 70
Endomorphisms are neither covariant nor contravariant functors - they are invariant functors. They may also be monomorphic functors. The mono-traversable package doesn't define a MonoFunctor instance for Endo, but that may just be an omission. It'd be an interesting exercise to see if such an instance is possible. I don't know yet, but I think that it is...
For now, though, I'm going to leave that as an exercise. Readers who manage to implement a lawful instance of MonoFunctor for Endo should send a pull request to the mono-traversable package.
Finally, a note on words. I agree that invariant functor would also have been a good description of monomorphic functors. It seems to me that in both mathematics and programming, there's sometimes a 'land-grab' of terms. The first person to think of a concept gets to pick the word. If the concept is compelling, the word may stick.
This strikes me as an unavoidable consequence of how knowledge progresses. Ideas rarely spring forth fully formed. Often, someone gets a half-baked idea and names it before fully understanding it. When later, more complete understanding emerges, it may be too late to change the terminology.
This has happened to me in this very article series, which I titled From design patterns to category theory before fully understanding where it'd lead me. I've later come to realise that we need only abstract algebra to describe monoids, semigroups, et cetera. Thus, the article series turned out to have little to do with category theory, but I couldn't (wouldn't) change the title and the URL of the original article, since it was already published.
The same may be the case with the terms invariant functors and monomorphic functors. Perhaps invariant functors should instead have been called isomorphic functors...
I've started a small article series on invariant functors.
Subjectivity
A subjective experience can be sublime, but it isn't an argument.
I once wrote a book. One of the most common adjectives people used about it was opinionated. That's okay. It is, I think, a ramification of the way I write. I prioritise writing so that you understand what I mean, and why I mean it. You can call that opinionated if you like.
This means that I frequently run into online arguments, mostly on Twitter. This particularly happens when I write something that readers don't like.
The sublime #
Whether or not you like something is a subjective experience. I have nothing against subjective experiences.
Subjective experiences fuel art. Before I became a programmer, I wanted to be an artist. I've loved French-Belgian comics for as long as I remember (my favourites have always been Hermann and Jean Giraud), and until I gave up in my mid-twenties, I wanted to become a graphic novelist.

This interest in drawing also fuelled a similar interest in paintings and art in general. I've had many sublime experiences in front of a work of art in various museums around the world. These were all subjective experiences that were precious to me.
For as long as I've been interested in graphic arts, I've also loved music. I've worn LPs thin in the 1970s and '80s. I've played guitar and wanted to be a rock star. I regularly get goosebumps from listing to outstanding music. These are all subjective experiences.
Having an experience is part of the human condition.
How you feel about something, however, isn't an argument.
Arguing about subjective experience #
I rarely read music reviews. How you experience music is such a personal experience that I find it futile to argue about it. Maybe you share my feelings that Army of Me is a sublime track, or maybe it leaves you cold. If you don't like that kind of music, I can't argue that you should.
Such a discussion generally takes place at the kindergarten level: "Army of Me is a great song!, "No it isn't," "Yes it is," and so on.
This doesn't mean that we can't talk about music (or, by extension, other subjective experiences). Talking about music can be exhilarating, particularly when you meet someone who shares your taste. Finding common ground, exploring and inspiring each other, learning about artists you didn't know about, is wonderful. It forges bonds between people. I suppose it's the same mechanism in which sports fans find common ground.
Sharing subjective experience may not be entirely futile. You can't use your feelings as an argument, but explaining why you feel a certain way can be illuminating. This is the realm of much art criticism. A good, popular and easily digestible example is the Strong Songs podcast. The host, Kirk Hamilton, likes plenty of music that I don't. I must admit, though, that his exigesis of Satisfied from Hamilton left me with more appreciation for that song than I normally have for that genre.
This is why, in a technical argument, when people say, "I don't like it", I ask why?
Your preference doesn't convince me to change my mind, but if you can explain your perspective, it may make me consider a point of which I wasn't aware.
It Depends™ #
Among other roles, I consult. Consultants are infamous for saying it depends, and obviously, if that's all we say, it'd be useless.
Most advice is given in a context. When a consultant starts a sentence with it depends, he or she must continue by explaining on what it depends. Done right, this can be tremendously valuable, because it gives the customer a framework they can use to make decisions.
In the same family as it depends, I often run into arguments like nothing is black or white, it's a trade-off, or other platitudes. Okay, it probably is a trade-off, but between what?
If it's a trade-off between my reasoned argument on the one hand, and someone's preference on the other hand, my reasoned argument wins.
Why? Because I can always trump with my preference as well.
Conclusion #
Our subjective experiences are important pieces of our lives. I hope that my detour around my love of art highlighted that I consider subjective experiences vital.
When we discuss how to do things, however, a preference isn't an argument. You may prefer to do things in one way, and I another. Such assertions, alone, don't move the discussion anywhere.
What we can do is to attempt to uncover the underlying causes for our preferences. There's no guarantee that we'll reach enlightenment, but it's certain that we'll get nowhere if we don't.
That's the reason that, when someone states "I prefer", I often ask why?
Comments
Consultants are infamous for saying it depends, and obviously, if that's all we say, it'd be useless.
Most advice is given in a context. When a consultant starts a sentence with it depends, he or she must continue by explaining on what it depends. Done right, this can be tremendously valuable, because it gives the customer a framework they can use to make decisions.
I have a vague memory of learning this through some smoothly worded saying. As I recall, it went something like this.
Anyone can say "It depends", but an expert can say on what it depends.
I don't think that is the exact phrase, because I don't think it sounds very smooth. Does anyone know of a succinct and smooth mnemonic phrase that captures this idea?
Fortunately, I don't squash my commits
The story of a bug, and how I addressed it.
Okay, I admit it: I could have given this article all sorts of alternative titles, each of which would have made as much sense as the one I chose. I didn't want to go with some of the other titles I had in mind, because they would give it all away up front. I didn't want to spoil the surprise.
I recently ran into this bug, it took me hours to troubleshoot it, and I was appalled when I realised what the problem was.
This is the story of that bug.
There are several insights from this story, and I admit that I picked the most click-baity one for the title.
Yak shaving #
I was working on the umpteenth variation of an online restaurant reservations system, and one of the features I'd added was a schedule only visible to the maître d'. The schedule includes a list of all reservations for a day, including guests' email addresses and so on. For that reason, I'd protected that resource by requiring a valid JSON Web Token (JWT) with an appropriate role.
The code discussed here is part of the sample code base that accompanies my book Code That Fits in Your Head.
I'd deployed a new version of the API and went for an ad-hoc test. To my surprise, that particular resource didn't work. When I tried to request it, I got a 403 Forbidden response.
"That's odd," I though, "it worked the last time I tried this."
The system is set up with continuous deployment. I push master to a remote repository, and a build pipeline takes over from there. It only deploys the new version if all tests pass, so my first reaction was that I might have made a mistake with the JWT.
I wasted significant time decoding the JWT and comparing its contents to what it was supposed to be. I couldn't find any problems.
I also meticulously compared the encryption key I'd used to sign the JWT with the key on the server. They were identical.
Incredulous, and running out of ideas, I tried running all tests on my development machine. Indeed, all 170 tests passed.
Finally, I gave up and ran the API on my development machine. It takes all of a 30 seconds to configure the code to run in that environment, so you're excused if you wonder why I didn't already do that. What can I say? I've almost two decades of experience with automated test suites. Usually, if all tests pass, the problem is environmental: a network topology issue, a bad or missing connection string, a misconfigured encryption key, an invalid JWT, things like that.
To my surprise, the problem also manifested on my machine.
Not my code #
Okay, even with hundreds of tests, perhaps some edge case went unnoticed. The only problem with that hypothesis was that this was hardly an edge case. I was only making a GET request with a Bearer token. I wasn't going through some convoluted sequence of steps.
GET /restaurants/1/schedule/2020/9/30 HTTP/1.1 Authorization: Bearer eyJhbGciOiJIUzI1NiIsInR5c[...]
I expected a successful response containing some JSON, but the result was 403 Forbidden. That was the same behaviour I saw in the production environment.
Now, to be clear, this is indeed a protected resource. If you present an invalid JWT, 403 Forbidden is the expected response. That's why I wasted a few hours looking for problems with the the JWT.
I finally, hesitatingly, concluded that the problem might be somewhere else. The JWT looked okay. So, hours into my troubleshooting I reluctantly set a breakpoint in my code and started the debugger. It isn't rational, but I tend to see it as a small personal defeat if I have to use the debugger. Even so, if used judiciously, it can be an effective way to identify problems.
The debugger never hit my breakpoint.
To be clear, the beginning of my Controller method looked like this:
[Authorize(Roles = "MaitreD")] [HttpGet("restaurants/{restaurantId}/schedule/{year}/{month}/{day}")] public async Task<ActionResult> Get( int restaurantId, int year, int month, int day) { if (!AccessControlList.Authorize(restaurantId)) return new ForbidResult();
My breakpoint was on the first line (the if conditional), but the debugger didn't break into it. When I issued my GET request, I immediately got the 403 Forbidden response. The breakpoint just sat there in the debugger, mocking me.
When that happens, it's natural to conclude that the problem occurs somewhere in the framework; in this case, ASP.NET. To test that hypothesis, I commented out the [Authorize] attribute and reissued the GET request. My hypothesis was that I'd get a 200 OK response, since the attribute is what tells ASP.NET to check authorisation.
The hypothesis held. The response was 200 OK.
Test interdependency #
I hate when that happens. It's up there with fixing other people's printers. The problem is in the framework, not in my code. I didn't have any authorisation callbacks registered, so I was fairly certain that the problem wasn't in my code.
I rarely jump to the conclusion that there's a bug in the framework. In my experience, select is rarely broken. My new hypothesis had to be that I'd somehow managed to misconfigure the framework.
But where? There were automated tests that verified that a client could request that resource with a valid JWT. There were other automated tests that verified what happened if you presented an invalid JWT, or none at all. And all tests were passing.
While I was fiddling with the tests, I eventually ran a parametrised test by itself, instead of the entire test suite:
[Theory] [InlineData( "Hipgnosta", 2024, 11, 2)] [InlineData( "Nono", 2018, 9, 9)] [InlineData("The Vatican Cellar", 2021, 10, 10)] public async Task GetRestaurantScheduleWhileAuthorized( string name, int year, int month, int day)
This parametrised test has three test cases. When I ran just that test method, two of the test cases passed, but one failed: the Nono case, for some reason I haven't yet figured out.
I didn't understand why that test case ought to fail while the others succeeded, but I had an inkling. I commented out the Nono test case and ran the test method again.
One passed and one failing test.
Now The Vatican Cellar test case was failing. I commented that out and ran the test method again. The remaining test case failed.
This reeks of some sort of test interdependency. Apparently, something happens during the first test run that makes succeeding tests pass, but it happens too late for the first one. But what?
Bisect #
Then something occurred to me that I should have thought of sooner. This feature used to work. Not only had the tests been passing, but I'd actually interacted with the deployed service, presenting a valid JWT and received a 200 OK response.
Once than dawned on me, I realised that it was just a manner of performing a binary search. Since, of course, I use version control, I had a version I knew worked, and a version that didn't work. The task, then, was to find the commit that introduced the defect.
As I've already implied, the system in question is an example code base. While I have a cloud-based production environment, none but I use it. It had been four or five days since I'd actually interacted with the real service, and I'd been busy making changes, trusting exclusively in my test suite. I tend to make frequent, small commits instead of big, infrequent commits, so I had accumulated about a hundred and fifty commits since the 'last known good' deployment.
Searching through hundreds of commits sounds overwhelming, but using binary search, it's actually not that bad. Pick the commit halfway between the 'last known good' commit and the most recent commit, and check it out. See if the defect is present there. If it is, you know that it was introduced somewhere between the commit you're looking at, and the 'last known good' commit. If it isn't present, it was introduced later. Regardless of the outcome, you know in which half to look. You now pick a new commit in the middle of that set and repeat the exercise. Even with, say, a hundred commits, the first bisection reduces the candidate set to 50, the next bisection to 25, then 13, then 7, 4, 2, and then you have it. If you do this systematically, you should find the exact commit in less than eight iterations.
This is, as far as I understand it, the algorithm used by Git bisect. You don't have to use the bisect command - the algorithm is easy enough to do by hand - but let's see how it works.
You start a bisect session with:
mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((93c6c35...)) $ git bisect start mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((93c6c35...)|BISECTING)
This starts an interactive session, which you can tell from the Git integration in Git Bash (it says BISECTING). You now mark a commit as being bad:
$ git bisect bad mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((93c6c35...)|BISECTING)
If you don't provide a commit ID at that point, Git is going to assume that you meant that the current commit (in this case 93c6c35) is bad. That's what I had in mind, so that's fine.
You now tell it about a commit ID that you know is good:
$ git bisect good 7dfdab2 Bisecting: 75 revisions left to test after this (roughly 6 steps) [1f78c9a90c2088423ab4fc145b7b2ec3859d6a9a] Use InMemoryRestaurantDatabase in a test mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((1f78c9a...)|BISECTING)
Notice that Git is already telling us how many iterations we should expect. You can also see that it checked out a new commit (1f78c9a) for you. That's the half-way commit.
At this point, I manually ran the test method with the three test cases. All three passed, so I marked that commit as good:
$ git bisect good Bisecting: 37 revisions left to test after this (roughly 5 steps) [5abf65a72628efabbf05fccd1b79340bac4490bc] Delete Either API mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((5abf65a...)|BISECTING)
Again, Git estimates how many more steps are left and checks out a new commit (5abf65a).
I repeated the process for each step, marking the commit as either good or bad, depending on whether or not the test passed:
$ git bisect bad Bisecting: 18 revisions left to test after this (roughly 4 steps) [fc48292b0d654f4f20522710c14d7726e6eefa70] Delete redundant Test Data Builders mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((fc48292...)|BISECTING) $ git bisect good Bisecting: 9 revisions left to test after this (roughly 3 steps) [b0cb1f5c1e9e40b1dabe035c41bfb4babfbe4585] Extract WillAcceptUpdate helper method mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((b0cb1f5...)|BISECTING) $ git bisect good Bisecting: 4 revisions left to test after this (roughly 2 steps) [d160c57288455377f8b0ad05985b029146228445] Extract ConfigureClock helper method mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((d160c57...)|BISECTING) $ git bisect good Bisecting: 2 revisions left to test after this (roughly 1 step) [4cb73c219565d8377aa67d79024d6836f9000935] Compact code mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((4cb73c2...)|BISECTING) $ git bisect good Bisecting: 0 revisions left to test after this (roughly 1 step) [34238c7d2606e9007b96b54b43e678589723520c] Extract CreateTokenValidationParameters method mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((34238c7...)|BISECTING) $ git bisect bad Bisecting: 0 revisions left to test after this (roughly 0 steps) [7d6583a97ff45fbd85878cecb5af11d93213a25d] Move Configure method up mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((7d6583a...)|BISECTING) $ git bisect good 34238c7d2606e9007b96b54b43e678589723520c is the first bad commit commit 34238c7d2606e9007b96b54b43e678589723520c Author: Mark Seemann <mark@example.com> Date: Wed Sep 16 07:15:12 2020 +0200 Extract CreateTokenValidationParameters method Restaurant.RestApi/Startup.cs | 32 +++++++++++++++++++------------- 1 file changed, 19 insertions(+), 13 deletions(-) mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((7d6583a...)|BISECTING)
Notice that the last step finds the culprit. It tells you which commit is the bad one, but surprisingly doesn't check it out for you. You can do that using a label Git has created for you:
$ git checkout refs/bisect/bad Previous HEAD position was 7d6583a Move Configure method up HEAD is now at 34238c7 Extract CreateTokenValidationParameters method mark@Vindemiatrix MINGW64 ~/Documents/Redacted/Restaurant ((34238c7...)|BISECTING)
You've now found and checked out the offending commit. Hopefully, the changes in that commit should give you a clue about the problem.
The culprit #
What's in that commit? Take a gander:
$ git show commit 34238c7d2606e9007b96b54b43e678589723520c (HEAD, refs/bisect/bad) Author: Mark Seemann <mark@example.com> Date: Wed Sep 16 07:15:12 2020 +0200 Extract CreateTokenValidationParameters method diff --git a/Restaurant.RestApi/Startup.cs b/Restaurant.RestApi/Startup.cs index 6c161b5..bcde861 100644 --- a/Restaurant.RestApi/Startup.cs +++ b/Restaurant.RestApi/Startup.cs @@ -79,10 +79,6 @@ namespace Ploeh.Samples.Restaurants.RestApi private void ConfigureAuthorization(IServiceCollection services) { - JwtSecurityTokenHandler.DefaultMapInboundClaims = false; - - var secret = Configuration["JwtIssuerSigningKey"]; - services.AddAuthentication(opts => { opts.DefaultAuthenticateScheme = @@ -91,15 +87,8 @@ namespace Ploeh.Samples.Restaurants.RestApi JwtBearerDefaults.AuthenticationScheme; }).AddJwtBearer(opts => { - opts.TokenValidationParameters = new TokenValidationParameters - { - ValidateIssuerSigningKey = true, - IssuerSigningKey = new SymmetricSecurityKey( - Encoding.ASCII.GetBytes(secret)), - ValidateIssuer = false, - ValidateAudience = false, - RoleClaimType = "role" - }; + opts.TokenValidationParameters = + CreateTokenValidationParameters(); opts.RequireHttpsMetadata = false; }); @@ -108,6 +97,23 @@ namespace Ploeh.Samples.Restaurants.RestApi sp.GetService<IHttpContextAccessor>().HttpContext.User)); } + private TokenValidationParameters CreateTokenValidationParameters() + { + JwtSecurityTokenHandler.DefaultMapInboundClaims = false; + + var secret = Configuration["JwtIssuerSigningKey"]; + + return new TokenValidationParameters + { + ValidateIssuerSigningKey = true, + IssuerSigningKey = new SymmetricSecurityKey( + Encoding.ASCII.GetBytes(secret)), + ValidateIssuer = false, + ValidateAudience = false, + RoleClaimType = "role" + }; + } + private void ConfigureRepository(IServiceCollection services) {
Can you spot the problem?
As soon as I saw that diff, the problem almost jumped out at me. I'm so happy that I make small commits. What you see here is, I promise, the entire diff of that commit.
Clearly, you're not familiar with this code base, but even so, you might be able to intuit the problem from the above diff. You don't need domain-specific knowledge for it, or knowledge of the rest of the code base.
I'll give you a hint: I moved a line of code into a lambda expression.
Deferred execution #
In the above commit, I extracted a helper method that I called CreateTokenValidationParameters. As the name communicates, it creates JWT validation parameters. In other words, it supplies the configuration values that determine how ASP.NET figures out how to authorise an HTTP request.
Among other things, it sets the RoleClaimType property to "role". By default, the [Authorize] attribute is looking for a role claim with a rather complicated identifier. Setting the RoleClaimType enables you to change the identifier. By setting it to "role", I'm telling the ASP.NET framework that it should look for claims named role in the JWT, and these should be translated to role claims.
Except that it doesn't work.
Ostensibly, this is for backwards compatibility reasons. You have to set JwtSecurityTokenHandler.DefaultMapInboundClaims to false. Notice that this is a global variable.
I thought that the line of code that does that conceptually belongs together with the other code that configures the JWT validation parameters, so I moved it in there. I didn't think much about it, and all my tests were still passing.
What happened, though, was that I moved mutation of a global variable into a helper method that was called from a lambda expression. Keep in mind that lambda expressions represent code that may run later; that execution is deferred.
By moving that mutation statement into the helper method, I inadvertently deferred its execution. When the application's Startup code runs, it configures the service. All the code that runs inside of AddJwtBearer, however, doesn't run immediately; it runs when needed.
This explains why all tests were passing. My test suite has plenty of self-hosted integration tests in the style of outside-in test-driven development. When I ran all the tests, the deferred code block would run in some other test context, flipping that global bit as a side effect. When the test suite reaches the test that fails when run in isolation, the bit is already flipped, and then it works.
It took me hours to figure out what the problem was, and it turned out that the root cause was a global variable.
Global variables are evil. Who knew?
Can't reproduce #
Once you figure out what the problem is, you should reproduce it with an automated test.
Yes, and how do I do that here? I already had tests that verify that you can GET the desired resource if you present a valid JWT. And that test passes!
The only way I can think of to reproduce the issue with an automated test is to create a completely new, independent test library with only one test. I considered doing that, weighed the advantages against the disadvantages and decided, given the context, that it wasn't worth the effort.
That means, though, that I had to accept that within the confines of my existing testing strategy, I can't reproduce the defect. This doesn't happen to me often. In fact, I can't recall that it's ever happened to me before, like this.
Resolution #
It took me hours to find the bug, and ten seconds to fix it. I just moved the mutation of JwtSecurityTokenHandler.DefaultMapInboundClaims back to the ConfigureAuthorization method:
diff --git a/Restaurant.RestApi/Startup.cs b/Restaurant.RestApi/Startup.cs index d4917f5..e40032f 100644 --- a/Restaurant.RestApi/Startup.cs +++ b/Restaurant.RestApi/Startup.cs @@ -79,6 +79,7 @@ namespace Ploeh.Samples.Restaurants.RestApi private void ConfigureAuthorization(IServiceCollection services) { + JwtSecurityTokenHandler.DefaultMapInboundClaims = false; services.AddAuthentication(opts => { opts.DefaultAuthenticateScheme = @@ -99,8 +100,6 @@ namespace Ploeh.Samples.Restaurants.RestApi private TokenValidationParameters CreateTokenValidationParameters() { - JwtSecurityTokenHandler.DefaultMapInboundClaims = false; - var secret = Configuration["JwtIssuerSigningKey"]; return new TokenValidationParameters
An ad-hoc smoke test verified that this solved the problem.
Conclusion #
There are multiple insights to be had from this experience:
- Global variables are evil
- Binary search, or bisection, is useful when troubleshooting
- Not all bugs can be reproduced by an automated test
- Small commits make it easy to detect problems
EnsureSuccessStatusCode as an assertion
It finally dawned on me that EnsureSuccessStatusCode is a fine test assertion.
Okay, I admit that sometimes I can be too literal and rigid in my thinking. At least as far back as 2012 I've been doing outside-in TDD against self-hosted HTTP APIs. When you do that, you'll regularly need to verify that an HTTP response is successful.
Assert equality #
You can, of course, write an assertion like this:
Assert.Equal(HttpStatusCode.OK, response.StatusCode);
If the assertion fails, it'll produce a comprehensible message like this:
Assert.Equal() Failure Expected: OK Actual: BadRequest
What's not to like?
Assert success #
The problem with testing strict equality in this context is that it's often too narrow a definition of success.
You may start by returning 200 OK as response to a POST request, but then later evolve the API to return 201 Created or 202 Accepted. Those status codes still indicate success, and are typically accompanied by more information (e.g. a Location header). Thus, evolving a REST API from returning 200 OK to 201 Created or 202 Accepted isn't a breaking change.
It does, however, break the above assertion, which may now fail like this:
Assert.Equal() Failure Expected: OK Actual: Created
You could attempt to fix this issue by instead verifying IsSuccessStatusCode:
Assert.True(response.IsSuccessStatusCode);
That permits the API to evolve, but introduces another problem.
Legibility #
What happens when an assertion against IsSuccessStatusCode fails?
Assert.True() Failure Expected: True Actual: False
That's not helpful. At least, you'd like to know which other status code was returned instead. You can address that concern by using an overload to Assert.True (most unit testing frameworks come with such an overload):
Assert.True( response.IsSuccessStatusCode, $"Actual status code: {response.StatusCode}.");
This produces more helpful error messages:
Actual status code: BadRequest. Expected: True Actual: False
Granted, the Expected: True, Actual: False lines are redundant, but at least the information you care about is there; in this example, the status code was 400 Bad Request.
Conciseness #
That's not bad. You can use that Assert.True overload everywhere you want to assert success. You can even copy and paste the code, because it's an idiom that doesn't change. Still, since I like to stay within 80 characters line width, this little phrase takes up three lines of code.
Surely, a helper method can address that problem:
internal static void AssertSuccess(this HttpResponseMessage response) { Assert.True( response.IsSuccessStatusCode, $"Actual status code: {response.StatusCode}."); }
I can now write a one-liner as an assertion:
response.AssertSuccess();
What's not to like?
Carrying coals to Newcastle #
If you're already familiar with the HttpResponseMessage class, you may have been reading this far with some frustration. It already comes with a method called EnsureSuccessStatusCode. Why not just use that instead?
response.EnsureSuccessStatusCode();
As long as the response status code is in the 200 range, this method call succeeds, but if not, it throws an exception:
Response status code does not indicate success: 400 (Bad Request).
That's exactly the information you need.
I admit that I can sometimes be too rigid in my thinking. I've known about this method for years, but I never thought of it as a unit testing assertion. It's as if there's a category in my programming brain that's labelled unit testing assertions, and it only contains methods that originate from unit testing.
I even knew about Debug.Assert, so I knew that assertions also exist outside of unit testing. That assertion isn't suitable for unit testing, however, so I never included it in my category of unit testing assertions.
The EnsureSuccessStatusCode method doesn't have assert in its name, but it behaves just like a unit testing assertion: it throws an exception with a useful error message if a criterion is not fulfilled. I just never thought of it as useful for unit testing purposes because it's part of 'production code'.
Conclusion #
The built-in EnsureSuccessStatusCode method is fine for unit testing purposes. Who knows, perhaps other class libraries contain similar assertion methods, although they may be hiding behind names that don't include assert. Perhaps your own production code contains such methods. If so, they can double as unit testing assertions.
I've been doing test-driven development for close to two decades now, and one of many consistent experiences is this:
- In the beginning of a project, the unit tests I write are verbose. This is natural, because I'm still getting to know the domain.
- After some time, I begin to notice patterns in my tests, so I refactor them. I introduce helper APIs in the test code.
- Finally, I realise that some of those unit testing APIs might actually be useful in the production code too, so I move them over there.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
Comments
Unfortunately, I can't agree that it's fine to use EnsureSuccessStatusCode or other similar methods for assertions. An exception of a kind different from assertion (XunitException for XUnit, AssertionException for NUnit) is handled in a bit different way by the testing framework. EnsureSuccessStatusCode method throws HttpRequestException. Basically, a test that fails with such exception is considered as "Failed by error".
For example, the test result message in case of 404 status produced by the EnsureSuccessStatusCode method is:
System.Net.Http.HttpRequestException : Response status code does not indicate success: 404 (Not Found).
Where "System.Net.Http.HttpRequestException :" text looks redundant, as we do assertion. This also may make other people think that the reason for this failure is not an assertion, but an unexpected exception. In case of regular assertion exception type, that text is missing.
Other points are related to NUnit:
-
There are 2 different failure test outcome kinds in NUnit:
- Failure: a test assertion failed. (Status=Failed, Label=empty)
- Error: an unexpected exception occurred. (Status=Failed, Label=Error)
- You can't use methods like
EnsureSuccessStatusCodeas assertion inside multiple asserts. - NUnit tracks the count of assertions for each test.
"assertions"property gets into the test results XML file and might be useful. This property increments on assertion methods,EnsureSuccessStatusCode- obviously doesn't increment it.
Yevgeniy, thank you for writing. This shows, I think, that all advice is contextual. It's been more than a decade since I regularly used NUnit, but I vaguely recall that it gives special treatment to its own assertion exceptions.
I also grant that the "System.Net.Http.HttpRequestException" part of the message is redundant. To make matters worse, even without that 'prologue' the information that we care about (the actual status code) is all the way to the right. It'll often require horizontal scrolling to see it.
That doesn't much bother me, though. I think that one should optimise for the most frequent scenario. For example, I favour taking a bit of extra time to write readable code, because the bottleneck in programming isn't typing. In the same vein, I find it a good trade-off being able to avoid adding more code against an occasional need to scroll horizontally. The cost of code isn't the time it takes to write it, but the maintenance burden it imposes, as well as the cognitive load it adds.
The point here is that while horizontal scrolling is inconvenient, the most frequent scenario is that tests don't fail. The inconvenience only manifests in the rare circumstance that a test fails.
I want to thank you, however, for pointing out the issues with NUnit. It reinforces the impression I already had of it, as a framework to stay away from. That design seems to me to impose a lock-in that prevents you from mixing NUnit with improved APIs.
In contrast, the xunit.core library doesn't include xunit.assert. I often take advantage of that when I write unit tests in F#. While the xUnit.net assertion library is adequate, Unquote is much better for F#. I appreciate that xUnit.net enables me to combine the tools that work best in a given situation.
I see your point, Mark. Thanks for your reply.
I would like to add a few words in defense of the NUnit.
First of all, there is no problem to use an extra library for NUnit assertions too. For example, I like FluentAssertions that works great for both XUnit and NUnit.
NUnit 3 also has a set of useful features that are missing in XUnit like:
- Multiple asserts - quite useful for UI testing, for example.
- Warnings.
- TestContext.
- File attachments - useful for UI tests or tests that verify files. For example, when the UI test fails, you can take a screenshot, save it and add to NUnit as an attachment. Or when you test PDF file, you can attach the file that doesn't pass the test.
I can recommend to reconsider the view of NUnit, as the library progressed well during its 3rd version. XUnit and NUnit seem interchangeable for unit testing. But NUnit, from my point of view, provides the features that are helpful in integration and UI testing.
Yevgeniy, I haven't done UI testing since sometime in 2005, I think, so I wasn't aware of that. It's good to know that NUnit may excel at that, and the other scenarios you point out.
To be clear, while I still think I may prefer xUnit.net, I don't consider it perfect.
I would like to mention FluentAssertions.Web, a library I wrote with the purpose to solve exact this problem I had while maintaining API tests. It's frustrating not to tell in two seconds why a test failed. Yeah, it is a Bad Request, but why. Maybe the response is in the respons content?
Wouldn't be an idea to see the response content? This FluentAssertions extension outputs everything starting from the request to the response, when the test fails.
Adrian, thank you for writing. Your comment inspired me to write an article on when tests fail. This article is now in the publication queue. I'll try to remember to come back here and add a link once it's published.
(Placeholder)
An XPath query for long methods
A filter for Visual Studio code metrics.
I consider it a good idea to limit the size of code blocks. Small methods are easier to troubleshoot and in general fit better in your head. When it comes to vertical size, however, the editors I use don't come with visual indicators like they do for horizontal size.
When you're in the midst of developing a feature, you don't want to be prevented from doing so by a tool that refuses to compile your code if methods get too long. On the other hand, it might be a good idea to regularly run a tool over your code base to identify which methods are getting too long.
With Visual Studio you can calculate code metrics, which include a measure of the number of lines of code for each method. One option produces an XML file, but if you have a large code base, those XML files are big.
The XML files typically look like this:
<?xml version="1.0" encoding="utf-8"?> <CodeMetricsReport Version="1.0"> <Targets> <Target Name="Restaurant.RestApi.csproj"> <Assembly Name="Ploeh.Samples.Restaurants.RestApi, ..."> <Metrics> <Metric Name="MaintainabilityIndex" Value="87" /> <Metric Name="CyclomaticComplexity" Value="537" /> <Metric Name="ClassCoupling" Value="208" /> <Metric Name="DepthOfInheritance" Value="1" /> <Metric Name="SourceLines" Value="3188" /> <Metric Name="ExecutableLines" Value="711" /> </Metrics> <Namespaces> <Namespace Name="Ploeh.Samples.Restaurants.RestApi"> <Metrics> <Metric Name="MaintainabilityIndex" Value="87" /> <Metric Name="CyclomaticComplexity" Value="499" /> <Metric Name="ClassCoupling" Value="204" /> <Metric Name="DepthOfInheritance" Value="1" /> <Metric Name="SourceLines" Value="3100" /> <Metric Name="ExecutableLines" Value="701" /> </Metrics> <Types> <NamedType Name="CalendarController"> <Metrics> <Metric Name="MaintainabilityIndex" Value="73" /> <Metric Name="CyclomaticComplexity" Value="14" /> <Metric Name="ClassCoupling" Value="34" /> <Metric Name="DepthOfInheritance" Value="1" /> <Metric Name="SourceLines" Value="190" /> <Metric Name="ExecutableLines" Value="42" /> </Metrics> <Members> <Method Name="Task<ActionResult> CalendarController.Get(..."> <Metrics> <Metric Name="MaintainabilityIndex" Value="64" /> <Metric Name="CyclomaticComplexity" Value="2" /> <Metric Name="ClassCoupling" Value="12" /> <Metric Name="SourceLines" Value="28" /> <Metric Name="ExecutableLines" Value="7" /> </Metrics> </Method> <!--Much more data goes here--> </Members> </NamedType> </Types> </Namespace> </Namespaces> </Assembly> </Target> </Targets> </CodeMetricsReport>
How can you filter such a file to find only those methods that are too long?
That sounds like a job for XPath. I admit, though, that I use XPath only rarely. While the general idea of the syntax is easy to grasp, it has enough subtle pitfalls that it's not that easy to use, either.
Partly for my own benefit, and partly for anyone else who might need it, here's an XPath query that looks for long methods:
//Members/child::*[Metrics/Metric[@Value > 24 and @Name = "SourceLines"]]
This query looks for methods longer that 24 lines of code. If you don't agree with that threshold you can always change it to another value. You can also change @Name to look for CyclomaticComplexity or one of the other metrics.
Given the above XML metrics report, the XPath filter would select (among other members) the CalendarController.Get method, because it has 28 lines of source code. It turns out, though, that the filter produces some false positives. The method in question is actually fine:
/* This method loads a year's worth of reservations in order to segment * them all. In a realistic system, this could be quite stressful for * both the database and the web server. Some of that concern can be * addressed with an appropriate HTTP cache header and a reverse proxy, * but a better solution would be a CQRS-style architecture where the * calendars get re-rendered as materialised views in a background * process. That's beyond the scope of this example code base, though. */ [ResponseCache(Duration = 60)] [HttpGet("restaurants/{restaurantId}/calendar/{year}")] public async Task<ActionResult> Get(int restaurantId, int year) { var restaurant = await RestaurantDatabase .GetRestaurant(restaurantId).ConfigureAwait(false); if (restaurant is null) return new NotFoundResult(); var period = Period.Year(year); var days = await MakeDays(restaurant, period) .ConfigureAwait(false); return new OkObjectResult( new CalendarDto { Name = restaurant.Name, Year = year, Days = days }); }
That method only has 18 lines of actual source code, from the beginning of the method declaration to the closing bracket. Visual Studio's metrics calculator, however, also counts the attributes and the comments.
In general, I only add comments when I want to communicate something that I can't express as a type or a method name, so in this particular code base, it's not much of an issue. If you consistently adorn every method with doc comments, on the other hand, you may need to perform some pre-processing on the source code before you calculate the metrics.

Comments
I find the idea of the impure/pure/impure sandwich rather interesting and I agree with the benefits that it yields. However, I was wondering about where to move synchronization logic, i.e. the reservation system should avoid double bookings. With the initial TrySave approach it would be clear for me where to put this logic: the synchonrization mechanism should be part of the TrySave method. With the impure/pure/impure sandwich, it will move out to the most outer layern (HTTP Controller) - at least this is how I'd see it. My feelings tells me that this is a bit smelly, but I can't really pin point why I think so. Can you give some advice on this? How would you solve that?
Johannes, thank you for writing. There are several ways to address that issue, depending on what sort of trade-off you're looking for. There's always a trade-off.
You can address the issue with a lock-free architecture. This typically involves expressing the desired action as a Command and putting it on a durable queue. If you combine that with a single-threaded, single-instance Actor that pulls Commands off the queue, you need no further transaction processing, because the architecture itself serialises writes. You can find plenty of examples of such an architecture on the internet, including (IIRC) my Pluralsight course Functional Architecture with F#.
Another option is to simply surround the impureim sandwich with a TransactionScope (if you're on .NET, that is).