ploeh blog danish software design
The Git repository that vanished
A pair of simple operations resurrected it.
The other day I had an 'interesting' experience. I was about to create a small pull request, so I checked out a new branch in Git and switched to my editor in order to start coding when the battery on my laptop died.
Clearly, when this happens, the computer immediately stops, without any graceful shutdown.
I plugged in the laptop and booted it. When I navigated to the source code folder I was working on, the files where there, but it was no longer a Git repository!
Git is fixable #
Git is more complex, and more powerful, than most developers care to deal with. Over the years, I've observed hundreds of people interact with Git in various ways, and most tend to give up at the first sign of trouble.
The point of this article isn't to point fingers at anyone, but rather to serve as a gentle reminder that Git tends to be eminently fixable.
Often, when people run into problems with Git, their only recourse is to delete the repository and clone it again. I've seen people do that enough times to realise that it might be helpful to point out: You may not have to do that.
Corruption #
Since I use Git tactically I have many repositories on my machine that have no remotes. In those cases, deleting the entire directory and cloning it from the remote isn't an option. I do take backups, though.
Still, in this story, the repository I was working with did have a remote. Even so, I was reluctant to delete everything and start over, since I had multiple branches and stashes I'd used for various experiments. Many of those I'd never pushed to the remote, so starting over would mean that I'd lose all of that. It was, perhaps, not a catastrophe, but I would certainly prefer to restore my local repository, if possible.
The symptoms were these: When you work with Git in Git Bash, the prompt will indicate which branch you're on. That information was absent, so I was already worried. A quick query confirmed my fears:
$ git status fatal: not a git repository (or any of the parent directories): .git
All the source code was there, but it looked as though the Git repository was gone. The code still compiled, but there was no source history.
Since all code files were there, I had hope. It helps knowing that Git, too, is file-based, and all files are in a hidden directory called .git. If all the source code was still there, perhaps the .git files were there, too. Why wouldn't they be?
$ ls .git COMMIT_EDITMSG description gitk.cache hooks/ info/ modules/ objects/ packed-refs config FETCH_HEAD HEAD index logs/ ms-persist.xml ORIG_HEAD refs/
Jolly good! The .git files were still there.
I now had a hypothesis: The unexpected shutdown of my machine had left some 'dangling pointers' in .git. A modern operating system may delay writes to disk, so perhaps my git checkout command had never made it all the way to disk - or, at least, not all of it.
If the repository was 'merely' corrupted in the sense that a few of the reference pointers had gone missing, perhaps it was fixable.
Empty-headed #
A few web searches indicated that the problem might be with the HEAD file, so I investigated its contents:
$ cat .git/HEAD
That was all. No output. The HEAD file was empty.
That file is not supposed to be empty. It's supposed to contain a commit ID or a reference that tells the Git CLI what the current head is - that is, which commit is currently checked out.
While I had checked out a new branch when my computer shut down, I hadn't written any code yet. Thus, the easiest remedy would be to restore the head to master. So I opened the HEAD file in Vim and added this to it:
ref: refs/heads/master
And just like that, the entire Git repository returned!
Bad object #
The branches, the history, everything looked as though it was restored. A little more investigation, however, revealed one more problem:
$ git log --oneline --all fatal: bad object refs/heads/some-branch
While a normal git log command worked fine, as soon as I added the --all switch, I got that bad object error message, with the name of the branch I had just created before the computer shut down. (The name of that branch wasn't some-branch - that's just a surrogate I'm using for this article.)
Perhaps this was the same kind of problem, so I explored the .git directory further and soon discovered a some-branch file in .git/refs/heads/. What did the contents look like?
$ cat .git/refs/heads/some-branch
Another empty file!
Since I had never committed any work to that branch, the easiest fix was to simply delete the file:
$ rm .git/refs/heads/some-branch
That solved that problem as well. No more fatal: bad object error when using the --all switch with git log.
No more problems have shown up since then.
Conclusion #
My experience with Git is that it's so powerful that you can often run into trouble. On the other hand, it's also so powerful that you can also use it to extricate yourself from trouble. Learning how to do that will teach you how to use Git to your advantage.
The problem that I ran into here wasn't fixable with the Git CLI itself, but turned out to still be easily remedied. A Git guru like Enrico Campidoglio could most likely have solved my problems without even searching the web. The details of how to solve the problems were new to me, but it took me a few web searches and perhaps five-ten minutes to fix them.
The point of this article, then, isn't in the details. It's that it pays to do a little investigation when you run into problems with Git. I already knew that, but I thought that this little story was a good occasion to share that knowledge.
Favour flat code file folders
How code files are organised is hardly related to sustainability of code bases.
My recent article Folders versus namespaces prompted some reactions. A few kind people shared how they organise code bases, both on Twitter and in the comments. Most reactions, however, carry the (subliminal?) subtext that organising code in file folders is how things are done.
I'd like to challenge that notion.
As is usually my habit, I mostly do this to make you think. I don't insist that I'm universally right in all contexts, and that everyone else are wrong. I only write to suggest that alternatives exist.
The previous article wasn't a recommendation; it's was only an exploration of an idea. As I describe in Code That Fits in Your Head, I recommend flat folder structures. Put most code files in the same directory.
Finding files #
People usually dislike that advice. How can I find anything?!
Let's start with a counter-question: How can you find anything if you have a deep file hierarchy? Usually, if you've organised code files in subfolders of subfolders of folders, you typically start with a collapsed view of the tree.
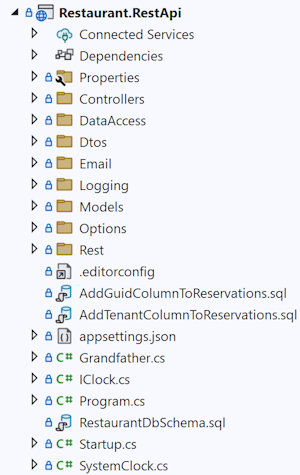
Those of my readers who know a little about search algorithms will point out that a search tree is an efficient data structure for locating content. The assumption, however, is that you already know (or can easily construct) the path you should follow.
In a view like the above, most files are hidden in one of the collapsed folders. If you want to find, say, the Iso8601.cs file, where do you look for it? Which path through the tree do you take?
Unfair!, you protest. You don't know what the Iso8601.cs file does. Let me enlighten you: That file contains functions that render dates and times in ISO 8601 formats. These are used to transmit dates and times between systems in a platform-neutral way.
So where do you look for it?
It's probably not in the Controllers or DataAccess directories. Could it be in the Dtos folder? Rest? Models?
Unless your first guess is correct, you'll have to open more than one folder before you find what you're looking for. If each of these folders have subfolders of their own, that only exacerbates the problem.
If you're curious, some programmer (me) decided to put the Iso8601.cs file in the Dtos directory, and perhaps you already guessed that. That's not the point, though. The point is this: 'Organising' code files in folders is only efficient if you can unerringly predict the correct path through the tree. You'll have to get it right the first time, every time. If you don't, it's not the most efficient way.
Most modern code editors come with features that help you locate files. In Visual Studio, for example, you just hit Ctrl+, and type a bit of the file name: iso:
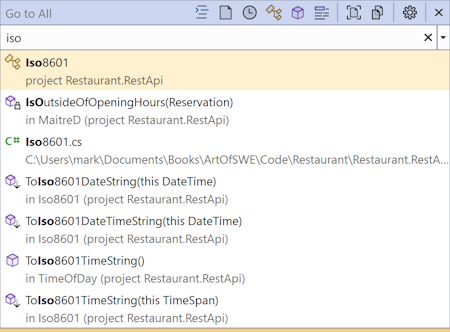
Then hit Enter to open the file. In Visual Studio Code, the corresponding keyboard shortcut is Ctrl+p, and I'd be highly surprised if other editors didn't have a similar feature.
To conclude, so far: Organising files in a folder hierarchy is at best on par with your editor's built-in search feature, but is likely to be less productive.
Navigating a code base #
What if you don't quite know the name of the file you're looking for? In such cases, the file system is even less helpful.
I've seen people work like this:
- Look at some code. Identify another code item they'd like to view. (Examples may include: Looking at a unit test and wanting to see the SUT, or looking at a class and wanting to see the base class.)
- Move focus to the editor's folder view (in Visual Studio called the Solution Explorer).
- Scroll to find the file in question.
- Double-click said file.
Regardless of how the files are organised, you could, instead, go to definition (F12 with my Visual Studio keyboard layout) in a single action. Granted, how well this works varies with editor and language. Still, even when editor support is less optimal (e.g. a code base with a mix of F# and C#, or a Haskell code base), I can often find things faster with a search (Ctrl+Shift+f) than via the file system.
A modern editor has efficient tools that can help you find what you're looking for. Looking through the file system is often the least efficient way to find the code you're looking for.
Large code bases #
Do I recommend that you dump thousands of code files in a single directory, then?
Hardly, but a question like that presupposes that code bases have thousands of code files. Or more, even. And I've seen such code bases.
Likewise, it's a common complaint that Visual Studio is slow when opening solutions with hundreds of projects. And the day Microsoft fixes that problem, people are going to complain that it's slow when opening a solution with thousands of projects.
Again, there's an underlying assumption: That a 'real' code base must be so big.
Consider alternatives: Could you decompose the code base into multiple smaller code bases? Could you extract subsystems of the code base and package them as reusable packages? Yes, you can do all those things.
Usually, I'd pull code bases apart long before they hit a thousand files. Extract modules, libraries, utilities, etc. and put them in separate code bases. Use existing package managers to distribute these smaller pieces of code. Keep the code bases small, and you don't need to organise the files.
Maintenance #
But, if all files are mixed together in a single folder, how do we keep the code maintainable?
Once more, implicit (but false) assumptions underlie such questions. The assumption is that 'neatly' organising files in hierarchies somehow makes the code easier to maintain. Really, though, it's more akin to a teenager who 'cleans' his room by sweeping everything off the floor only to throw it into his cupboard. It does enable hoovering the floor, but it doesn't make it easier to find anything. The benefit is mostly superficial.
Still, consider a tree.
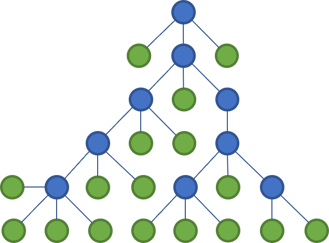
This may not be the way you're used to see files and folders rendered, but this diagram emphases the tree structure and makes what happens next starker.
The way that most languages work, putting code files in folders makes little difference to the compiler. If the classes in my Controllers folder need some classes from the Dtos folder, you just use them. You may need to import the corresponding namespace, but modern editors make that a breeze.
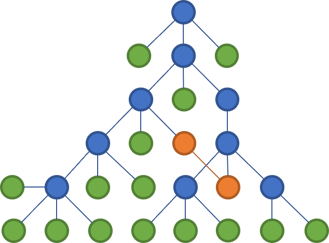
In the above tree, the two files who now communicate are coloured orange. Notice that they span across two main branches of the tree.
Thus, even though the files are organised in a tree, it has no impact on the maintainability of the code base. Code can reference other code in other parts of the tree. You can easily create cycles in a language like C#, and organising files in trees makes no difference.
Most languages, however, enforce that library dependencies form a directed acyclic graph (i.e. if the data access library references the domain model, the domain model can't reference the data access library). The C# (and most other languages) compiler enforces what Robert C. Martin calls the Acyclic Dependencies Principle. Preventing cycles prevents spaghetti code, which is key to a maintainable code base.
(Ironically, one of the more controversial features of F# is actually one of its greatest strengths: It doesn't allow cycles.)
Tidiness #
Even so, I do understand the lure of organising code files in an elaborate hierarchy. It looks so neat.
Previously, I've touched on the related topic of consistency, and while I'm a bit of a neat freak myself, I have to realise that tidiness seems to be largely unrelated to the sustainability of a code base.
As another example in this category, I've seen more than one code base with consistently beautiful documentation. Every method was adorned with formal XML documentation with every input parameter as well as output described.
Every new phase in a method was delineated with another neat comment, nicely adorned with a 'comment frame' and aligned with other comments.
It was glorious.
Alas, that documentation sat on top of 750-line methods with a cyclomatic complexity above 50. The methods were so long that developers had to introduce artificial variable scopes to avoid naming collisions.
The reason I was invited to look at that code in the first place was that the organisation had trouble with maintainability, and they asked me to help.
It was neat, yet unmaintainable.
This discussion about tidiness may seem like a digression, but I think it's important to make the implicit explicit. If I'm not much mistaken, preference for order is a major reason that so many developers want to organise code files into hierarchies.
Organising principles #
What other motivations for file hierarchies could there be? How about the directory structure as an organising principle?
The two most common organising principles are those that I experimented with in the previous article:
- By technical role (Controller, View Model, DTO, etc.)
- By feature
A technical leader might hope that, by presenting a directory structure to team members, it imparts an organising principle on the code to be.
It may even do so, but is that actually a benefit?
It might subtly discourage developers from introducing code that doesn't fit into the predefined structure. If you organise code by technical role, developers might put most code in Controllers, producing mostly procedural Transaction Scripts. If you organise by feature, this might encourage duplication because developers don't have a natural place to put general-purpose code.
You can put truly shared code in the root folder, the counter-argument might be. This is true, but:
- This seems to be implicitly discouraged by the folder structure. After all, the hierarchy is there for a reason, right? Thus, any file you place in the root seems to suggest a failure of organisation.
- On the other hand, if you flaunt that not-so-subtle hint and put many code files in the root, what advantage does the hierarchy furnish?
In Information Distribution Aspects of Design Methodology David Parnas writes about documentation standards:
"standards tend to force system structure into a standard mold. A standard [..] makes some assumptions about the system. [...] If those assumptions are violated, the [...] organization fits poorly and the vocabulary must be stretched or misused."
(The above quote is on the surface about documentation standards, and I've deliberately butchered it a bit (clearly marked) to make it easier to spot the more general mechanism.)
In the same paper, Parnas describes the danger of making hard-to-change decisions too early. Applied to directory structure, the lesson is that you should postpone designing a file hierarchy until you know more about the problem. Start with a flat directory structure and add folders later, if at all.
Beyond files? #
My claim is that you don't need much in way of directory hierarchy. From this doesn't follow, however, that we may never leverage such options. Even though I left most of the example code for Code That Fits in Your Head in a single folder, I did add a specialised folder as an anti-corruption layer. Folders do have their uses.
"Why not take it to the extreme and place most code in a single file? If we navigate by "namespace view" and search, do we need all those files?"
Following a thought to its extreme end can shed light on a topic. Why not, indeed, put all code in a single file?
Curious thought, but possibly not new. I've never programmed in SmallTalk, but as I understand it, the language came with tooling that was both IDE and execution environment. Programmers would write source code in the editor, but although the code was persisted to disk, it may not have been as text files.
Even if I completely misunderstand how SmallTalk worked, it's not inconceivable that you could have a development environment based directly on a database. Not that I think that this sounds like a good idea, but it sounds technically possible.
Whether we do it one way or another seems mostly to be a question of tooling. What problems would you have if you wrote an entire C# (Java, Python, F#, or similar) code base as a single file? It becomes more difficult to look at two or more parts of the code base at the same time. Still, Visual Studio can actually give you split windows of the same file, but I don't know how it scales if you need multiple views over the same huge file.
Conclusion #
I recommend flat directory structures for code files. Put most code files in the root of a library or app. Of course, if your system is composed from multiple libraries (dependencies), each library has its own directory.
Subfolders aren't prohibited, only generally discouraged. Legitimate reasons to create subfolders may emerge as the code base evolves.
My misgivings about code file directory hierarchies mostly stem from the impact they have on developers' minds. This may manifest as magical thinking or cargo-cult programming: Erect elaborate directory structures to keep out the evil spirits of spaghetti code.
It doesn't work that way.
Visual Studio Code snippet to make URLs relative
Yes, it involves JSON and regular expressions.
Ever since I migrated the blog off dasBlog I've been writing the articles in raw HTML. The reason is mostly a historical artefact: Originally, I used Windows Live Writer, but Jekyll had no support for that, and since I'd been doing web development for more than a decade already, raw HTML seemed like a reliable and durable alternative. I increasingly find that relying on skill and knowledge is a far more durable strategy than relying on technology.
For a decade I used Sublime Text to write articles, but over the years, I found it degrading in quality. I only used Sublime Text to author blog posts, so when I recently repaved my machine, I decided to see if I could do without it.
Since I was already using Visual Studio Code for much of my programming, I decided to give it a go for articles as well. It always takes time when you decide to move off a tool you've been used for a decade, but after some initial frustrations, I quickly found a new modus operandi.
One benefit of rocking the boat is that it prompts you to reassess the way you do things. Naturally, this happened here as well.
My quest for relative URLs #
I'd been using a few Sublime Text snippets to automate a few things, like the markup for the section heading you see above this paragraph. Figuring out how to replicate that snippet in Visual Studio Code wasn't too hard, but as I was already perusing the snippet documentation, I started investigating other options.
One little annoyance I'd lived with for years was adding links to other articles on the blog.
While I write an article, I run the site on my local machine. When linking to other articles, I sometimes use the existing page address off the public site, and sometimes I just copy the page address from localhost. In both cases, I want the URL to be relative so that I can navigate the site even if I'm offline. I've written enough articles on planes or while travelling without internet that this is an important use case for me.
For example, if I want to link to the article Adding NuGet packages when offline, I want the URL to be /2023/01/02/adding-nuget-packages-when-offline, but that's not the address I get when I copy from the browser's address bar. Here, I get the full URL, with either http://localhost:4000/ or https://blog.ploeh.dk/ as the origin.
For years, I've been manually stripping the origin away, as well as the trailing /. Looking through the Visual Studio Code snippet documentation, however, I eyed an opportunity to automate that workflow.
Snippet #
I wanted a piece of editor automation that could modify a URL after I'd pasted it into the article. After a few iterations, I've settled on a surround-with snippet that works pretty well. It looks like this:
"Make URL relative": { "prefix": "urlrel", "body": [ "${TM_SELECTED_TEXT/^(?:http(?:s?):\\/\\/(?:[^\\/]+))(.+)\\//$1/}" ], "description": "Make URL relative." }
Don't you just love regular expressions? Write once, scrutinise forever.
I don't want to go over all the details, because I've already forgotten most of them, but essentially this expression strips away the URL origin starting with either http or https until it finds the first slash /.
The thing that makes it useful, though, is the TM_SELECTED_TEXT variable that tells Visual Studio Code that this snippet works on selected text.
When I paste a URL into an a tag, at first nothing happens because no text is selected. I can then use Shift + Alt + → to expand the selection, at which point the Visual Studio Code lightbulb (Code Action) appears:

Running the snippet removes the URL's origin, as well as the trailing slash, and I can move on to write the link text.
Conclusion #
After I started using Visual Studio Code to write blog posts, I've created a few custom snippets to support my authoring workflow. Most of them are fairly mundane, but the make-URLs-relative snippet took me a few iterations to get right.
I'm not expecting many of my readers to have this particular need, but I hope that this outline showcases the capabilities of Visual Studio Code snippets, and perhaps inspires you to look into creating custom snippets for your own purposes.
Folders versus namespaces
What if you allow folder and namespace structure to diverge?
I'm currently writing C# code with some first-year computer-science students. Since most things are new to them, they sometimes do things in a way that are 'not the way we usually do things'. As an example, teachers have instructed them to use namespaces, but apparently no-one have told them that the file folder structure has to mirror the namespace structure.
The compiler doesn't care, but as long as I've been programming in C#, it's been idiomatic to do it that way. There's even a static code analysis rule about it.
The first couple of times they'd introduce a namespace without a corresponding directory, I'd point out that they are supposed to keep those things in sync. One day, however, it struck me: What happens if you flout that convention?
A common way to organise code files #
Code scaffolding tools and wizards will often nudge you to organise your code according to technical concerns: Controllers, models, views, etc. I'm sure you've encountered more than one code base organised like this:
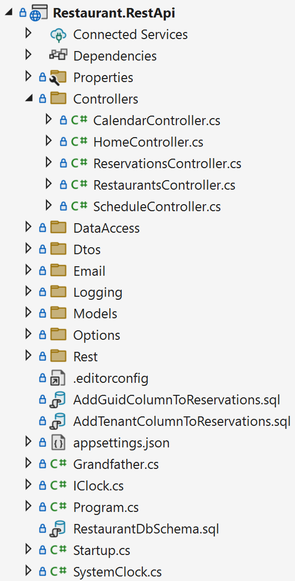
You'll put all your Controller classes in the Controllers directory, and make sure that the namespace matches. Thus, in such a code base, the full name of the ReservationsController might be Ploeh.Samples.Restaurants.RestApi.Controllers.ReservationsController.
A common criticism is that this is the wrong way to organise the code.
The problem with trees #
The complaint that this is the wrong way to organise code implies that a correct way exists. I write about this in Code That Fits in Your Head:
Should you create a subdirectory for Controllers, another for Models, one for Filters, and so on? Or should you create a subdirectory for each feature?
Few people like my answer: Just put all files in one directory. Be wary of creating subdirectories just for the sake of 'organising' the code.
File systems are hierarchies; they are trees: a specialised kind of acyclic graph in which any two vertices are connected by exactly one path. Put another way, each vertex can have at most one parent. Even more bluntly: If you put a file in a hypothetical
Controllersdirectory, you can't also put it in aCalendardirectory.
But what if you could?
Namespaces disconnected from directory hierarchy #
The code that accompanies Code That Fits in Your Head is organised as advertised: 65 files in a single directory. (Tests go in separate directories, though, as they belong to separate libraries.)
If you decide to ignore the convention that namespace structure should mirror folder structure, however, you now have a second axis of variability.
As an experiment, I decided to try that idea with the book's code base. The above screen shot shows the stereotypical organisation according to technical responsibility, after I moved things around. To be clear: This isn't how the book's example code is organised, but an experiment I only now carried out.
If you open the ReservationsController.cs file, however, I've now declared that it belongs to a namespace called Ploeh.Samples.Restaurants.RestApi.Reservations. Using Visual Studio's Class View, things look different from the Solution Explorer:
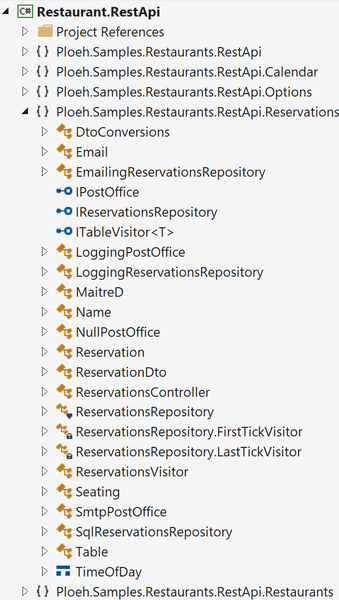
Here I've organised the namespaces according to feature, rather than technical role. The screen shot shows the Reservations feature opened, while other features remain closed.
Initial reactions #
This article isn't a recommendation. It's nothing but an initial exploration of an idea.
Do I like it? So far, I think I still prefer flat directory structures. Even though this idea gives two axes of variability, you still have to make judgment calls. It's easy enough with Controllers, but where do you put cross-cutting concerns? Where do you put domain logic that seems to encompass everything else?
As an example, the code base that accompanies Code That Fits in Your Head is a multi-tenant system. Each restaurant is a separate tenant, but I've modelled restaurants as part of the domain model, and I've put that 'feature' in its own namespace. Perhaps that's a mistake; at least, I now have the code wart that I have to import the Ploeh.Samples.Restaurants.RestApi.Restaurants namespace to implement the ReservationsController, because its constructor looks like this:
public ReservationsController( IClock clock, IRestaurantDatabase restaurantDatabase, IReservationsRepository repository) { Clock = clock; RestaurantDatabase = restaurantDatabase; Repository = repository; }
The IRestaurantDatabase interface is defined in the Restaurants namespace, but the Controller needs it in order to look up the restaurant (i.e. tenant) in question.
You could argue that this isn't a problem with namespaces, but rather a code smell indicating that I should have organised the code in a different way.
That may be so, but then implies a deeper problem: Assigning files to hierarchies may not, after all, help much. It looks as though things are organised, but if the assignment of things to buckets is done without a predictable system, then what benefit does it provide? Does it make things easier to find, or is the sense of order mostly illusory?
I tend to still believe that this is the case. This isn't a nihilistic or defeatist position, but rather a realisation that order must arise from other origins.
Conclusion #
I was recently repeatedly encountering student code with a disregard for the convention that namespace structure should follow directory structure (or the other way around). Taking a cue from Kent Beck I decided to investigate what happens if you forget about the rules and instead pursue what that new freedom might bring.
In this article, I briefly show an example where I reorganised a code base so that the file structure is according to implementation detail, but the namespace hierarchy is according to feature. Clearly, I could also have done it the other way around.
What if, instead of two, you have three organising principles? I don't know. I can't think of a third kind of hierarchy in a language like C#.
After a few hours reorganising the code, I'm not scared away from this idea. It might be worth to revisit in a larger code base. On the other hand, I'm still not convinced that forcing a hierarchy over a sophisticated software design is particularly beneficial.
P.S. 2023-05-30. This article is only a report on an experiment. For my general recommendation regarding code file organisation, see Favour flat code file folders.
Comments
Hi Mark,
While reading your book "Code That Fits in Your Head", your latest blog entry caught my attention, as I am struggling in software development with similar issues.
I find it hard, to put all classes into one project directory, as it feels overwhelming, when the number of classes increases.
In the following, I would like to specify possible organising principles in my own words.
Postulations
- Folders should help the programmer (and reader) to keep the code organised
- Namespaces should reflect the hierarchical organisation of the code base
- Cross-cutting concerns should be addressed by modularity.
Definitions
1. Folders
- the allocation of classes in a project with similar technical concerns into folders should help the programmer in the first place, by visualising this similarity
- the benefit lies just in the organisation, i.e. storage of code, not in the expression of hierarchy
2. Namespaces
- expression of hierarchy can be achieved by namespaces, which indicate the relationship between allocated classes
- classes can be organised in folders with same designation
- the namespace designation could vary by concerns, although the classes are placed in same folders, as the technical concern of the class shouldn't affect the hierarchical organisation
3. Cross-cutting concerns
- classes, which aren't related to a single task, could be indicated by a special namespace
- they could be placed in a different folder, to signalize different affiliations
- or even placed in a different assembly
Summing up
A hierarchy should come by design. The organisation of code in folders should help the programmer or reader to grasp the file structure, not necessarily the program hierarchy.
Folders should be a means, not an expression of design. Folders and their designations could change (or disappear) over time in development. Thus, explicit connection of namespace to folder designation seems not desirable, but it's not forbidden.
Best regards,
Markus
Markus, thank you for writing. You can, of course, organise code according to various principles, and what works in one case may not be the best fit in another case. The main point of this article was to suggest, as an idea, that folder hierarchy and namespace hierarchy doesn't have to match.
Based on reader reactions, however, I realised that I may have failed to clearly communicate my fundamental position, so I wrote another article about that. I do, indeed, favour flat folder hierarchies.
That is not to say that you can't have any directories in your code base, but rather that I'm sceptical that any such hierarchy addresses real problems.
For instance, you write that
"Folders should help the programmer (and reader) to keep the code organised"
If I focus on the word should, then I agree: Folders should help the programmer keep the code organised. In my view, then, it follows that if a tree structure does not assist in doing that, then that structure is of no use and should not be implemented (or abandoned if already in place).
I do get the impression from many people that they consider a directory tree vital to be able to navigate and understand a code base. What I've tried to outline in my more recent article is that I don't accept that as an undisputable axiom.
What I do find helpful as an organising principle is focusing on dependencies as a directed acyclic graph. Cyclic dependencies between objects is a main source of complexity. Keep dependency graphs directed and make code easy to delete.
Organising code files in a tree structure doesn't help achieve that goal. This is the reason I consider code folder hierarchies a red herring: Perhaps not explicitly detrimental to sustainability, but usually nothing but a distraction.
How, then, do you organise a large code base? I hope that I answer that question, too, in my more recent article Favour flat code file folders.
Is cyclomatic complexity really related to branch coverage?
A genuine case of doubt and bewilderment.
Regular readers of this blog may be used to its confident and opinionated tone. I write that way, not because I'm always convinced that I'm right, but because prose with too many caveats and qualifications tends to bury the message in verbose and circumlocutory ambiguity.
This time, however, I write to solicit feedback, and because I'm surprised to the edge of bemusement by a recent experience.
Collatz sequence #
Consider the following code:
public static class Collatz { public static IReadOnlyCollection<int> Sequence(int n) { if (n < 1) throw new ArgumentOutOfRangeException( nameof(n), $"Only natural numbers allowed, but given {n}."); var sequence = new List<int>(); var current = n; while (current != 1) { sequence.Add(current); if (current % 2 == 0) current = current / 2; else current = current * 3 + 1; } sequence.Add(current); return sequence; } }
As the names imply, the Sequence function calculates the Collatz sequence for a given natural number.
Please don't tune out if that sounds mathematical and difficult, because it really isn't. While the Collatz conjecture still evades mathematical proof, the sequence is easy to calculate and understand. Given a number, produce a sequence starting with that number and stop when you arrive at 1. Every new number in the sequence is based on the previous number. If the input is even, divide it by two. If it's odd, multiply it by three and add one. Repeat until you arrive at one.
The conjecture is that any natural number will produce a finite sequence. That's the unproven part, but that doesn't concern us. In this article, I'm only interested in the above code, which computes such sequences.
Here are few examples:
> Collatz.Sequence(1) List<int>(1) { 1 } > Collatz.Sequence(2) List<int>(2) { 2, 1 } > Collatz.Sequence(3) List<int>(8) { 3, 10, 5, 16, 8, 4, 2, 1 } > Collatz.Sequence(4) List<int>(3) { 4, 2, 1 }
While there seems to be a general tendency for the sequence to grow as the input gets larger, that's clearly not a rule. The examples show that the sequence for 3 is longer than the sequence for 4.
All this, however, just sets the stage. The problem doesn't really have anything to do with Collatz sequences. I only ran into it while working with a Collatz sequence implementation that looked a lot like the above.
Cyclomatic complexity #
What is the cyclomatic complexity of the above Sequence function? If you need a reminder of how to count cyclomatic complexity, this is a good opportunity to take a moment to refresh your memory, count the number, and compare it with my answer.
Apart from the opportunity for exercise, it was a rhetorical question. The answer is 4.
This means that we'd need at least four unit test to cover all branches. Right? Right?
Okay, let's try.
Branch coverage #
Before we start, let's make the ritual denouncement of code coverage as a target metric. The point isn't to reach 100% code coverage as such, but to gain confidence that you've added tests that cover whatever is important to you. Also, the best way to do that is usually with TDD, which isn't the situation I'm discussing here.
The first branch that we might want to cover is the Guard Clause. This is easily addressed with an xUnit.net test:
[Fact] public void ThrowOnInvalidInput() { Assert.Throws<ArgumentOutOfRangeException>(() => Collatz.Sequence(0)); }
This test calls the Sequence function with 0, which (in this context, at least) isn't a natural number.
If you measure test coverage (or, in this case, just think it through), there are no surprises yet. One branch is covered, the rest aren't. That's 25%.
(If you use the free code coverage option for .NET, it will surprisingly tell you that you're only at 16% branch coverage. It deems the cyclomatic complexity of the Sequence function to be 6, not 4, and 1/6 is 16.67%. Why it thinks it's 6 is not entirely clear to me, but Visual Studio agrees with me that the cyclomatic complexity is 4. In this particular case, it doesn't matter anyway. The conclusion that follows remains the same.)
Let's add another test case, and perhaps one that gives the algorithm a good exercise.
[Fact] public void Example() { var actual = Collatz.Sequence(5); Assert.Equal(new[] { 5, 16, 8, 4, 2, 1 }, actual); }
As expected, the test passes. What's the branch coverage now?
Try to think it through instead of relying exclusively on a tool. The algorithm isn't more complicated that you can emulate execution in your head, or perhaps with the assistance of a notepad. How many branches does it execute when the input is 5?
Branch coverage is now 100%. (Even the dotnet coverage tool agrees, despite its weird cyclomatic complexity value.) All branches are exercised.
Two tests produce 100% branch coverage of a function with a cyclomatic complexity of 4.
Surprise #
That's what befuddles me. I thought that cyclomatic complexity and branch coverage were related. I thought, that the number of branches was a good indicator of the number of tests you'd need to cover all branches. I even wrote an article to that effect, and no-one contradicted me.
That, in itself, is no proof of anything, but the notion that the article presents seems to be widely accepted. I never considered it controversial, and the only reason I didn't cite anyone is that this seems to be 'common knowledge'. I wasn't aware of a particular source I could cite.
Now, however, it seems that it's wrong. Is it wrong, or am I missing something?
To be clear, I completely understand why the above two tests are sufficient to fully cover the function. I also believe that I fully understand why the cyclomatic complexity is 4.
I am also painfully aware that the above two tests in no way fully specify the Collatz sequence. That's not the point.
The point is that it's possible to cover this function with only two tests, despite the cyclomatic complexity being 4. That surprises me.
Is this a known thing?
I'm sure it is. I've long since given up discovering anything new in programming.
Conclusion #
I recently encountered a function that performed a Collatz calculation similar to the one I've shown here. It exhibited the same trait, and since it had no Guard Clause, I could fully cover it with a single test case. That function even had a cyclomatic complexity of 6, so you can perhaps imagine my befuddlement.
Is it wrong, then, that cyclomatic complexity suggests a minimum number of test cases in order to cover all branches?
It seems so, but that's new to me. I don't mind being wrong on occasion. It's usually an opportunity to learn something new. If you have any insights, please leave a comment.
Comments
My first thought is that the code looks like an unrolled recursive function, so perhaps if it's refactored into a driver function and a "continuation passing style" it might make the cyclomatic complexity match the covering tests.
So given the following:
public delegate void ResultFunc(IEnumerable<int> result);
public delegate void ContFunc(int n, ResultFunc result, ContFunc cont);
public static void Cont(int n, ResultFunc result, ContFunc cont) {
if (n == 1) {
result(new[] { n });
return;
}
void Result(IEnumerable<int> list) => result(list.Prepend(n));
if (n % 2 == 0)
cont(n / 2, Result, cont);
else
cont(n * 3 + 1, Result, cont);
}
public static IReadOnlyCollection<int> Continuation(int n) {
if (n < 1)
throw new ArgumentOutOfRangeException(
nameof(n),
$"Only natural numbers allowed, but given {n}.");
var output = new List<int>();
void Output(IEnumerable<int> list) => output = list.ToList();
Cont(n, Output, Cont);
return output;
}
I calculate the Cyclomatic complexity of Continuation to be 2 and Step to be 3.
And it would seem you need 5 tests to properly cover the code, 3 for Step and 2 for Continuation.
But however you write the "n >=1" case for Continuation you will have to cover some of Step.
There is a relation between cyclomatic complexity and branches to cover, but it's not one of equality, cyclomatic complexity is an upper bound for the number of branches. There's a nice example illustrating this in the Wikipedia article on cyclomatic complexity that explains this, as well as the relation with path coverage (for which cyclomatic complexity is a lower bound).
I find cyclomatic complexity to be overly pedantic at times, and you will need four tests if you get really pedantic. First, test the guard clause as you already did. Then, test with 1 in order to test the
whileloop body not being run. Then, test with 2 in order to test that the
whileis executed, but we only hit the
ifpart of the
if/else. Finally, test with 3 in order to hit the
elseinside of the
while. That's four tests where each test is only testing one of the branches (some tests hit more than one branch, but the "extra branch" is already covered by another test). Again, this is being really pedantic and I wouldn't test this function as laid out above (I'd probaby put in the test with 1, since it's an edge case, but otherwise test as you did).
I don't think there's a rigorous relationship between cyclomatic complexity and number of tests. In simple cases, treating things as though the relationship exists can be helpful. But once you start having iterrelated branches in a function, things get murky, and you may have to go to pedantic lengths in order to maintain the relationship. The same thing goes for code coverage, which can be 100% even though you haven't actually tested all paths through your code if there are multiple branches in the function that depend on each other.
Thank you, all, for writing. I'm extraordinarily busy at the moment, so it'll take me longer than usual to respond. Rest assured, however, that I haven't forgotten.
If we agree to the definition of cyclomatic complexity as the number of independent paths through a section of code, then the number of tests needed to cover that section must be the same per definition, if those tests are also independent. Independence is crucial here, and is also the main source of confusion. Both the while and if forks depend on the same variable (current), and so they are not independent.
The second test you wrote is similarly not independent, as it ends up tracing multiple paths through through if: odd for 5, and even for 16, 8, etc, and so ends up covering all paths. Had you picked 2 instead of 5 for the test, that would have been more independent, as it would not have traced the else path, requiring one additional test.
The standard way of computing cyclomatic complexity assumes independence, which simply is not possible in this case.
Struan, thank you for writing, and please accept my apologies for the time it took me to respond. I agree with your calculations of cyclomatic complexity of your refactored code.
I agree with what you write, but you can't write a sentence like "however you write the "n >=1" case for [...] you will have to cover some of [..]" and expect me to just ignore it. To be clear, I agree with you in the particular case of the methods you provided, but you inspired me to refactor my code with that rule as a specific constraint. You can see the results in my new article Collatz sequences by function composition.
Thank you for the inspiration.
Jeroen, thank you for writing, and please accept my apologies for the time it took me to respond. I should have read that Wikipedia article more closely, instead of just linking to it.
What still puzzles me is that I've been aware of, and actively used, cyclomatic complexity for more than a decade, and this distinction has never come up, and no-one has called me out on it.
As Cunningham's law says, the best way to get the right answer on the Internet is not to ask a question; it's to post the wrong answer. Even so, I posted Put cyclomatic complexity to good use in 2019, and no-one contradicted it.
I don't mention this as an argument that I'm right. Obviously, I was wrong, but no-one told me. Have I had something in my teeth all these years, too?
Brett, thank you for writing, and please accept my apologies for the time it took me to respond. I suppose that I failed to make my overall motivation clear. When doing proper test-driven development (TDD), one doesn't need cyclomatic complexity in order to think about coverage. When following the red-green-refactor checklist, you only add enough code to pass all tests. With that process, cyclomatic complexity is rarely useful, and I tend to ignore it.
I do, however, often coach programmers in unit testing and TDD, and people new to the technique often struggle with basics. They add too much code, instead of the simplest thing that could possibly work, or they can't think of a good next test case to write.
When teaching TDD I sometimes suggest cyclomatic complexity as a metric to help decision-making. Did we add more code to the System Under Test than warranted by tests? Is it okay to forgo writing a test of a one-liner with cyclomatic complexity of one?
The metric is also useful in hybrid scenarios where you already have production code, and now you want to add characterisation tests: Which test cases should you at least write?
Another way to answer such questions is to run a code-coverage tool, but that often takes time. I find it useful to teach people about cyclomatic complexity, because it's a lightweight heuristic always at hand.
Nikola, thank you for writing. The emphasis on independence is useful; I used compatible thinking in my new article Collatz sequences by function composition. By now, including the other comments to this article, it seems that we've been able to cover the problem better, and I, at least, feel that I've learned something.
I don't think, however, that the standard way of computing cyclomatic complexity assumes independence. You can easily compute the cyclomatic complexity of the above Sequence function, even though its branches aren't independent. Tooling such as Visual Studio seems to agree with me.
Refactoring pure function composition without breaking existing tests
An example modifying a Haskell Gossiping Bus Drivers implementation.
This is an article in an series of articles about the epistemology of interaction testing. In short, this collection of articles discusses how to test the composition of pure functions. While a pure function is intrinsically testable, how do you test the composition of pure functions? As the introductory article outlines, I consider it mostly a matter of establishing confidence. With enough test coverage you can be confident that the composition produces the desired outputs.
Keep in mind that if you compose pure functions into a larger pure function, the composition is still pure. This implies that you can still test it by supplying input and verifying that the output is correct.
Tests that exercise the composition do so by verifying observable behaviour. This makes them more robust to refactoring. You'll see an example of that later in this article.
Gossiping bus drivers #
I recently did the Gossiping Bus Drivers kata in Haskell. At first, I added the tests suggested in the kata description.
{-# OPTIONS_GHC -Wno-type-defaults #-}
module Main where
import GossipingBusDrivers
import Test.HUnit
import Test.Framework.Providers.HUnit (hUnitTestToTests)
import Test.Framework (defaultMain)
main :: IO ()
main = defaultMain $ hUnitTestToTests $ TestList [
"Kata examples" ~: do
(routes, expected) <-
[
([[3, 1, 2, 3],
[3, 2, 3, 1],
[4, 2, 3, 4, 5]],
Just 5),
([[2, 1, 2],
[5, 2, 8]],
Nothing)
]
let actual = drive routes
return $ expected ~=? actual
]
As I prefer them, these tests are parametrised HUnit tests.
The problem with those suggested test cases is that they don't provide enough confidence that an implementation is correct. In fact, I wrote this implementation to pass them:
drive routes = if length routes == 3 then Just 5 else Nothing
This is clearly incorrect. It just looks at the number of routes and returns a fixed value for each count. It doesn't look at the contents of the routes.
Even if you don't try to deliberately cheat I'm not convinced that these two tests are enough. You could try to write the correct implementation, but how do you know that you've correctly dealt with various edge cases?
Helper function #
The kata description isn't hard to understand, so while the suggested test cases seem insufficient, I knew what was required. Perhaps I could write a proper implementation without additional tests. After all, I was convinced that it'd be possible to do it with a cyclomatic complexity of 1, and since a test function also has a cyclomatic complexity of 1, there's always that tension in test-driven development: Why write test code to exercise code with a cyclomatic complexity of 1?.
To be clear: There are often good reasons to write tests even in this case, and this seems like one of them. Cyclomatic complexity indicates a minimum number of test cases, not necessarily a sufficient number.
Even though Haskell's type system is expressive, I soon found myself second-guessing the behaviour of various expressions that I'd experimented with. Sometimes I find GHCi (the Haskell REPL) sufficiently edifying, but in this case I thought that I might want to keep some test cases around for a helper function that I was developing:
import Data.List import qualified Data.Map.Strict as Map import Data.Map.Strict ((!)) import qualified Data.Set as Set import Data.Set (Set) evaluateStop :: (Functor f, Foldable f, Ord k, Ord a) => f (k, Set a) -> f (k, Set a) evaluateStop stopsAndDrivers = let gossip (stop, driver) = Map.insertWith Set.union stop driver gossipAtStops = foldl' (flip gossip) Map.empty stopsAndDrivers in fmap (\(stop, _) -> (stop, gossipAtStops ! stop)) stopsAndDrivers
I was fairly confident that this function worked as I intended, but I wanted to be sure. I needed some examples, so I added these tests:
"evaluateStop examples" ~: do (stopsAndDrivers, expected) <- [ ([(1, fromList [1]), (2, fromList [2]), (1, fromList [1])], [(1, fromList [1]), (2, fromList [2]), (1, fromList [1])]), ([(1, fromList [1]), (2, fromList [2]), (1, fromList [2])], [(1, fromList [1, 2]), (2, fromList [2]), (1, fromList [1, 2])]), ([(1, fromList [1, 2, 3]), (1, fromList [2, 3, 4])], [(1, fromList [1, 2, 3, 4]), (1, fromList [1, 2, 3, 4])]) ] let actual = evaluateStop stopsAndDrivers return $ fromList expected ~=? fromList actual
They do, indeed, pass.
The idea behind that evaluateStop function is to evaluate the state at each 'minute' of the simulation. The first line of each test case is the state before the drivers meet, and the second line is the expected state after all drivers have gossiped.
My plan was to use some sort of left fold to keep evaluating states until all information has disseminated to all drivers.
Property #
Since I have already extolled the virtues of property-based testing in this article series, I wondered whether I could add some properties instead of relying on examples. Well, I did manage to add one QuickCheck property:
testProperty "drive image" $ \ (routes :: [NonEmptyList Int]) -> let actual = drive $ fmap getNonEmpty routes in isJust actual ==> all (\i -> 0 <= i && i <= 480) actual
There's not much to talk about here. The property only states that the result of the drive function must be between 0 and 480, if it exists.
Such a property could vacuously pass if drive always returns Nothing, so I used the ==> QuickCheck combinator to make sure that the property is actually exercising only the Just cases.
Since the drive function only returns a number, apart from verifying its image I couldn't think of any other general property to add.
You can always come up with more specific properties that explicitly set up more constrained test scenarios, but is it worth it?
It's always worthwhile to stop and think. If you're writing a 'normal' example-based test, consider whether a property would be better. Likewise, if you're about to write a property, consider whether an example would be better.
'Better' can mean more than one thing. Preventing regressions is one thing, but making the code maintainable is another. If you're writing a property that is too complicated, it might be better to write a simpler example-based test.
I could definitely think of some complicated properties, but I found that more examples might make the test code easier to understand.
More examples #
After all that angst and soul-searching, I added a few more examples to the first parametrised test:
"Kata examples" ~: do (routes, expected) <- [ ([[3, 1, 2, 3], [3, 2, 3, 1], [4, 2, 3, 4, 5]], Just 5), ([[2, 1, 2], [5, 2, 8]], Nothing), ([[1, 2, 3, 4, 5], [5, 6, 7, 8], [3, 9, 6]], Just 13), ([[1, 2, 3], [2, 1, 3], [2, 4, 5, 3]], Just 5), ([[1, 2], [2, 1]], Nothing), ([[1]], Just 0), ([[2], [2]], Just 1) ] let actual = drive routes return $ expected ~=? actual
The first two test cases are the same as before, and the last two are some edge cases I added myself. The middle three I adopted from another page about the kata. Since those examples turned out to be off by one, I did those examples on paper to verify that I understood what the expected value was. Then I adjusted them to my one-indexed results.
Drive #
The drive function now correctly implements the kata, I hope. At least it passes all the tests.
drive :: (Num b, Enum b, Ord a) => [[a]] -> Maybe b drive routes = -- Each driver starts with a single gossip. Any kind of value will do, as -- long as each is unique. Here I use the one-based index of each route, -- since it fulfills the requirements. let drivers = fmap Set.singleton [1 .. length routes] goal = Set.unions drivers stops = transpose $ fmap (take 480 . cycle) routes propagation = scanl (\ds ss -> snd <$> evaluateStop (zip ss ds)) drivers stops in fmap fst $ find (all (== goal) . snd) $ zip [0 ..] propagation
Haskell code can be information-dense, and if you don't have an integrated development environment (IDE) around, this may be hard to read.
drivers is a list of sets. Each set represents the gossip that a driver knows. At the beginning, each only knows one piece of gossip. The expression initialises each driver with a singleton set. Each piece of gossip is represented by a number, simply going from 1 to the number of routes. Incidentally, this is also the number of drivers, so you can consider the number 1 as a placeholder for the gossip that driver 1 knows, and so on.
The goal is the union of all the gossip. Once every driver's knowledge is equal to the goal the simulation can stop.
Since evaluateStop simulates one stop, the drive function needs a list of stops to fold. That's the stops value. In the very first example, you have three routes: [3, 1, 2, 3], [3, 2, 3, 1], and [4, 2, 3, 4, 5]. The first time the drivers stop (after one minute), the stops are 3, 3, and 4. That is, the first element in stops would be the list [3, 3, 4]. The next one would be [1, 2, 2], then [2, 3, 3], and so on.
My plan all along was to use some sort of left fold to repeatedly run evaluateStop over each minute. Since I need to produce a list of states, scanl was an appropriate choice. The lambda expression that I have to pass to it, though, is more complicated than I appreciate. We'll return to that in a moment.
The drive function can now index the propagation list by zipping it with the infinite list [0 ..], find the first element where all sets are equal to the goal set, and then return that index. That produces the correct results.
The need for a better helper function #
As I already warned, I wasn't happy with the lambda expression passed to scanl. It looks complicated and arcane. Is there a better way to express the same behaviour? Usually, when confronted with a nasty lambda expression like that, in Haskell my first instinct is to see if pointfree.io has a better option. Alas, (((snd <$>) . evaluateStop) .) . flip zip hardly seems an improvement. That flip zip expression to the right, however, suggests that it might help flipping the arguments to evaluateStop.
When I developed the evaluateStop helper function, I found it intuitive to define it over a list of tuples, where the first element in the tuple is the stop, and the second element is the set of gossip that the driver at that stop knows.
The tuples don't have to be in that order, though. Perhaps if I flip the tuples that would make the lambda expression more readable. It was worth a try.
Confidence #
Since this article is part of a small series about the epistemology of testing composed functions, let's take a moment to reflect on the confidence we may have in the drive function.
Keep in mind the goal of the kata: Calculate the number of minutes it takes for all gossip to spread to all drivers. There's a few tests that verify that; seven examples and a fairly vacuous QuickCheck property. Is that enough to be confident that the function is correct?
If it isn't, I think the best option you have is to add more examples. For the sake of argument, however, let's assume that the tests are good enough.
When summarising the tests that cover the drive function, I didn't count the three examples that exercise evaluateStop. Do these three test cases improve your confidence in the drive function? A bit, perhaps, but keep in mind that the kata description doesn't mandate that function. It's just a helper function I created in order to decompose the problem.
Granted, having tests that cover a helper function does, to a degree, increase my confidence in the code. I have confidence in the function itself, but that is largely irrelevant, because the problem I'm trying to solve is not implementing this particular function. On the other hand, my confidence in evaluateStop means that I have increased confidence in the code that calls it.
Compared to interaction-based testing, I'm not testing that drive calls evaluateStop, but I can still verify that this happens. I can just look at the code.
The composition is already there in the code. What do I gain from replicating that composition with Stubs and Spies?
It's not a breaking change if I decide to implement drive in a different way.
What gives me confidence when composing pure functions isn't that I've subjected the composition to an interaction-based test. Rather, it's that the function is composed from trustworthy components.
Strangler #
My main grievance with Stubs and Spies is that they break encapsulation. This may sound abstract, but is a real problem. This is the underlying reason that so many tests break when you refactor code.
This example code base, as other functional code that I write, avoids interaction-based testing. This makes it easier to refactor the code, as I will now demonstrate.
My goal is to change the evaluateStop helper function by flipping the tuples. If I just edit it, however, I'm going to (temporarily) break the drive function.
Katas typically result in small code bases where you can get away with a lot of bad practices that wouldn't work in a larger code base. To be honest, the refactoring I have in mind can be completed in a few minutes with a brute-force approach. Imagine, however, that we can't break compatibility of the evaluateStop function for the time being. Perhaps, had we had a larger code base, there were other code that depended on this function. At the very least, the tests do.
Instead of brute-force changing the function, I'm going to make use of the Strangler pattern, as I've also described in my book Code That Fits in Your Head.
Leave the existing function alone, and add a new one. You can typically copy and paste the existing code and then make the necessary changes. In that way, you break neither client code nor tests, because there are none.
evaluateStop' :: (Functor f, Foldable f, Ord k, Ord a) => f (Set a, k) -> f (Set a, k) evaluateStop' driversAndStops = let gossip (driver, stop) = Map.insertWith Set.union stop driver gossipAtStops = foldl' (flip gossip) Map.empty driversAndStops in fmap (\(_, stop) -> (gossipAtStops ! stop, stop)) driversAndStops
In a language like C# you can often get away with overloading a method name, but Haskell doesn't have overloading. Since I consider this side-by-side situation to be temporary, I've appended a prime after the function name. This is a fairly normal convention in Haskell, I gather.
The only change this function represents is that I've swapped the tuple order.
Once you've added the new function, you may want to copy, paste and edit the tests. Or perhaps you want to do the tests first. During this process, make micro-commits so that you can easily suspend your 'refactoring' activity if something more important comes up.
Once everything is in place, you can change the drive function:
drive :: (Num b, Enum b, Ord a) => [[a]] -> Maybe b drive routes = -- Each driver starts with a single gossip. Any kind of value will do, as -- long as each is unique. Here I use the one-based index of each route, -- since it fulfills the requirements. let drivers = fmap Set.singleton [1 .. length routes] goal = Set.unions drivers stops = transpose $ fmap (take 480 . cycle) routes propagation = scanl (\ds ss -> fst <$> evaluateStop' (zip ds ss)) drivers stops in fmap fst $ find (all (== goal) . snd) $ zip [0 ..] propagation
Notice that the type of drive hasn't change, and neither has the behaviour. This means that although I've changed the composition (the interaction) no tests broke.
Finally, once I moved all code over, I deleted the old function and renamed the new one to take its place.
Was it all worth it? #
At first glance, it doesn't look as though much was gained. What happens if I eta-reduce the new lambda expression?
drive :: (Num b, Enum b, Ord a) => [[a]] -> Maybe b drive routes = -- Each driver starts with a single gossip. Any kind of value will do, as -- long as each is unique. Here I use the one-based index of each route, -- since it fulfills the requirements. let drivers = fmap Set.singleton [1 .. length routes] goal = Set.unions drivers stops = transpose $ fmap (take 480 . cycle) routes propagation = scanl (((fmap fst . evaluateStop) .) . zip) drivers stops in fmap fst $ find (all (== goal) . snd) $ zip [0 ..] propagation
Not much better. I can now fit the propagation expression on a single line of code and still stay within a 80x24 box, but that's about it. Is ((fmap fst . evaluateStop) .) . zip more readable than what we had before?
Hardly, I admit. I might consider reverting, and since I've been using Git tactically, I have that option.
If I hadn't tried, though, I wouldn't have known.
Conclusion #
When composing one pure function with another, how can you test that the outer function correctly calls the inner function?
By the same way that you test any other pure function. The only way you can observe whether a pure function works as intended is to compare its actual output to the output you expect its input to produce. How it arrives at that output is irrelevant. It could be looking up all results in a big table. As long as the result is correct, the function is correct.
In this article, you saw an example of how to test a composed function, as well as how to refactor it without breaking tests.
Next: When is an implementation detail an implementation detail?
Are pull requests bad because they originate from open-source development?
I don't think so, and at least find the argument flawed.
Increasingly I come across a quote that goes like this:
Pull requests were invented for open source projects where you want to gatekeep changes from people you don't know and don't trust to change the code safely.
If you're wondering where that 'quote' comes from, then read on. I'm not trying to stand up a straw man, but I had to do a bit of digging in order to find the source of what almost seems like a meme.
Quote investigation #
The quote is usually attributed to Dave Farley, who is a software luminary that I respect tremendously. Even with the attribution, the source is typically missing, but after asking around, Mitja Bezenšek pointed me in the right direction.
The source is most likely a video, from which I've transcribed a longer passage:
"Pull requests were invented to gatekeep access to open-source projects. In open source, it's very common that not everyone is given free access to changing the code, so contributors will issue a pull request so that a trusted person can then approve the change.
"I think this is really bad way to organise a development team.
"If you can't trust your team mates to make changes carefully, then your version control system is not going to fix that for you."
I've made an effort to transcribe as faithfully as possible, but if you really want to be sure what Dave Farley said, watch the video. The quote comes twelve minutes in.
My biases #
I agree that the argument sounds compelling, but I find it flawed. Before I proceed to put forward my arguments I want to make my own biases clear. Arguing against someone like Dave Farley is not something I take lightly. As far as I can tell, he's worked on systems more impressive than any I can showcase. I also think he has more industry experience than I have.
That doesn't necessarily make him right, but on the other hand, why should you side with me, with my less impressive résumé?
My objective is not to attack Dave Farley, or any other person for that matter. My agenda is the argument itself. I do, however, find it intellectually honest to cite sources, with the associated risk that my argument may look like a personal attack. To steelman my opponent, then, I'll try to put my own biases on display. To the degree I'm aware of them.
I prefer pull requests over pair and ensemble programming. I've tried all three, and I do admit that real-time collaboration has obvious advantages, but I find pairing or ensemble programming exhausting.
Since I read Quiet a decade ago, I've been alert to the introspective side of my personality. Although I agree with Brian Marick that one should be wary of understanding personality traits as destiny, I mostly prefer solo activities.
Increasingly, since I became self-employed, I've arranged my life to maximise the time I can work from home. The exercise regimen I've chosen for myself is independent of other people: I run, and lift weights at home. You may have noticed that I like writing. I like reading as well. And, hardly surprising, I prefer writing code in splendid isolation.
Even so, I find it perfectly possible to have meaningful relationships with other people. After all, I've been married to the same woman for decades, my (mostly) grown kids haven't fled from home, and I have friends that I've known for decades.
In a toot that I can no longer find, Brian Marick asked (and I paraphrase from memory): If you've tried a technique and didn't like it, what would it take to make you like it?
As a self-professed introvert, social interaction does tire me, but I still enjoy hanging out with friends or family. What makes those interactions different? Well, often, there's good food and wine involved. Perhaps ensemble programming would work better for me with a bottle of Champagne.
Other forces influence my preferences as well. I like the flexibility provided by asynchrony, and similarly dislike having to be somewhere at a specific time.
Having to be somewhere also involves transporting myself there, which I also don't appreciate.
In short, I prefer pull requests over pairing and ensemble programming. All of that, however, is just my subjective opinion, and that's not an argument.
Counter-examples #
The above tirade about my biases is not a refutation of Dave Farley's argument. Rather, I wanted to put my own blind spots on display. If you suspect me of motivated reasoning, that just might be the case.
All that said, I want to challenge the argument.
First, it includes an appeal to trust, which is a line of reasoning with which I don't agree. You can't trust your colleagues, just like you can't trust yourself. A code review serves more purposes than keeping malicious actors out of the code base. It also helps catch mistakes, security issues, or misunderstandings. It can also improve shared understanding of common goals and standards. Yes, this is also possible with other means, such as pair or ensemble programming, but from that, it doesn't follow that code reviews can't do that. They can. I've lived that dream.
If you take away the appeal to trust, though, there isn't much left of the argument. What remains is essentially: Pull requests were invented to solve a particular problem in open-source development. Internal software development is not open source. Pull requests are bad for internal software development.
That an invention was done in one context, however, doesn't preclude it from being useful in another. Git was invented to address an open-source problem. Should we stop using Git for internal software development?
Solar panels were originally developed for satellites and space probes. Does that mean that we shouldn't use them on Earth?
GPS was invented for use by the US military. Does that make civilian use wrong?
Are pull requests bad? #
I find the original argument logically flawed, but if I insist on logic, I'm also obliged to admit that my possible-world counter-examples don't prove that pull requests are good.
Dave Farley's claim may still turn out to be true. Not because of the argument he gives, but perhaps for other reasons.
I think I understand where the dislike of pull requests come from. As they are often practised, pull requests can sit for days with no-one looking at them. This creates unnecessary delays. If this is the only way you know of working with pull requests, no wonder you don't like them.
I advocate a more agile workflow for pull requests. I consider that congruent with my view on agile development.
Conclusion #
Pull requests are often misused, but they don't have to be. On the other hand, that's just my experience and subjective preference.
Dave Farley has argued that pull requests are a bad way to organise a development team. I've argued that the argument is logically flawed.
The question remains unsettled. I've attempted to refute one particular argument, and even if you accept my counter-examples, pull requests may still be bad. Or good.
Comments
Another important angle, for me, is that pull requests are not merely code review. It can also be a way of enforcing a variety of automated checks, i.e. running tests or linting etc. This enforces quality too - so I'd argue to use pull requests even if you don't do peer review (I do on my hobby projects atleast, for the exact reasons you mentioned in On trust in software development - I don't trust myself to be perfect.)
Casper, thank you for writing. Indeed, other readers have made similar observations on other channels (Twitter, Mastodon). That, too, can be a benefit.
In order to once more steel-man 'the other side', they'd probably say that you can run automated checks in your Continuous Delivery pipeline, and halt it if automated checks fail.
When done this way, it's useful to be able to also run the same tests on your dev box. I consider that a good practice anyway.
A restaurant example of refactoring from example-based to property-based testing
A C# example with xUnit.net and FsCheck.
This is the second comprehensive example that accompanies the article Epistemology of interaction testing. In that article, I argue that in a code base that leans toward functional programming (FP), property-based testing is a better fit than interaction-based testing. In this example, I will show how to refactor realistic state-based tests into (state-based) property-based tests.
The previous article showed a minimal and self-contained example that had the advantage of being simple, but the disadvantage of being perhaps too abstract and unrelatable. In this article, then, I will attempt to show a more realistic and concrete example. It actually doesn't start with interaction-based testing, since it's already written in the style of Functional Core, Imperative Shell. On the other hand, it shows how to refactor from concrete example-based tests to property-based tests.
I'll use the online restaurant reservation code base that accompanies my book Code That Fits in Your Head.
Smoke test #
I'll start with a simple test which was, if I remember correctly, the second test I wrote for this code base. It was a smoke test that I wrote to drive a walking skeleton. It verifies that if you post a valid reservation request to the system, you receive an HTTP response in the 200 range.
[Fact] public async Task PostValidReservation() { using var api = new LegacyApi(); var expected = new ReservationDto { At = DateTime.Today.AddDays(778).At(19, 0) .ToIso8601DateTimeString(), Email = "katinka@example.com", Name = "Katinka Ingabogovinanana", Quantity = 2 }; var response = await api.PostReservation(expected); response.EnsureSuccessStatusCode(); var actual = await response.ParseJsonContent<ReservationDto>(); Assert.Equal(expected, actual, new ReservationDtoComparer()); }
Over the lifetime of the code base, I embellished and edited the test to reflect the evolution of the system as well as my understanding of it. Thus, when I wrote it, it may not have looked exactly like this. Even so, I kept it around even though other, more detailed tests eventually superseded it.
One characteristic of this test is that it's quite concrete. When I originally wrote it, I hard-coded the date and time as well. Later, however, I discovered that I had to make the time relative to the system clock. Thus, as you can see, the At property isn't a literal value, but all other properties (Email, Name, and Quantity) are.
This test is far from abstract or data-driven. Is it possible to turn such a test into a property-based test? Yes, I'll show you how.
A word of warning before we proceed: Tests with concrete, literal, easy-to-understand examples are valuable as programmer documentation. A person new to the code base can peruse such tests and learn about the system. Thus, this test is already quite valuable as it is. In a real, living code base, I'd prefer leaving it as it is, instead of turning it into a property-based test.
Since it's a simple and concrete test, on the other hand, it's easy to understand, and thus also a a good place to start. Thus, I'm going to refactor it into a property-based test; not because I think that you should (I don't), but because I think it'll be easy for you, the reader, to follow along. In other words, it's a good introduction to the process of turning a concrete test into a property-based test.
Adding parameters #
This code base already uses FsCheck so it makes sense to stick to that framework for property-based testing. While it's written in F# you can use it from C# as well. The easiest way to use it is as a parametrised test. This is possible with the FsCheck.Xunit glue library. In fact, as I refactor the PostValidReservation test, it'll look much like the AutoFixture-driven tests from the previous article.
When turning concrete examples into properties, it helps to consider whether literal values are representative of an equivalence class. In other words, is that particular value important, or is there a wider set of values that would be just as good? For example, why is the test making a reservation 778 days in the future? Why not 777 or 779? Is the value 778 important? Not really. What's important is that the reservation is in the future. How far in the future actually isn't important. Thus, we can replace the literal value 778 with a parameter:
[Property] public async Task PostValidReservation(PositiveInt days) { using var api = new LegacyApi(); var expected = new ReservationDto { At = DateTime.Today.AddDays((int)days).At(19, 0) .ToIso8601DateTimeString(), // The rest of the test...
Notice that I've replaced the literal value 778 with the method parameter days. The PositiveInt type is a type from FsCheck. It's a wrapper around int that guarantees that the value is positive. This is important because we don't want to make a reservation in the past. The PositiveInt type is a good choice because it's a type that's already available with FsCheck, and the framework knows how to generate valid values. Since it's a wrapper, though, the test needs to unwrap the value before using it. This is done with the (int)days cast.
Notice, also, that I've replaced the [Fact] attribute with the [Property] attribute that comes with FsCheck.Xunit. This is what enables FsCheck to automatically generate test cases and feed them to the test method. You can't always do this, as you'll see later, but when you can, it's a nice and succinct way to express a property-based test.
Already, the PostValidReservation test method is 100 test cases (the FsCheck default), rather than one.
What about Email and Name? Is it important for the test that these values are exactly katinka@example.com and Katinka Ingabogovinanana or might other values do? The answer is that it's not important. What's important is that the values are valid, and essentially any non-null string is. Thus, we can replace the literal values with parameters:
[Property] public async Task PostValidReservation( PositiveInt days, StringNoNulls email, StringNoNulls name) { using var api = new LegacyApi(); var expected = new ReservationDto { At = DateTime.Today.AddDays((int)days).At(19, 0) .ToIso8601DateTimeString(), Email = email.Item, Name = name.Item, Quantity = 2 }; var response = await api.PostReservation(expected); response.EnsureSuccessStatusCode(); var actual = await response.ParseJsonContent<ReservationDto>(); Assert.Equal(expected, actual, new ReservationDtoComparer()); }
The StringNoNulls type is another FsCheck wrapper, this time around string. It ensures that FsCheck will generate no null strings. This time, however, a cast isn't possible, so instead I had to pull the wrapped string out of the value with the Item property.
That's enough conversion to illustrate the process.
What about the literal values 19, 0, or 2? Shouldn't we parametrise those as well? While we could, that takes a bit more effort. The problem is that with these values, any old positive integer isn't going to work. For example, the number 19 is the hour component of the reservation time; that is, the reservation is for 19:00. Clearly, we can't just let FsCheck generate any positive integer, because most integers aren't going to work. For example, 5 doesn't work because it's in the early morning, and the restaurant isn't open at that time.
Like other property-based testing frameworks FsCheck has an API that enables you to constrain value generation, but it doesn't work with the type-based approach I've used so far. Unlike PositiveInt there's no TimeBetween16And21 wrapper type.
You'll see what you can do to control how FsCheck generates values, but I'll use another test for that.
Parametrised unit test #
The PostValidReservation test is a high-level smoke test that gives you an idea about how the system works. It doesn't, however, reveal much about the possible variations in input. To drive such behaviour, I wrote and evolved the following state-based test:
[Theory] [InlineData(1049, 19, 00, "juliad@example.net", "Julia Domna", 5)] [InlineData(1130, 18, 15, "x@example.com", "Xenia Ng", 9)] [InlineData( 956, 16, 55, "kite@example.edu", null, 2)] [InlineData( 433, 17, 30, "shli@example.org", "Shanghai Li", 5)] public async Task PostValidReservationWhenDatabaseIsEmpty( int days, int hours, int minutes, string email, string name, int quantity) { var at = DateTime.Now.Date + new TimeSpan(days, hours, minutes, 0); var db = new FakeDatabase(); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var expected = new Reservation( new Guid("B50DF5B1-F484-4D99-88F9-1915087AF568"), at, new Email(email), new Name(name ?? ""), quantity); await sut.Post(expected.ToDto()); Assert.Contains(expected, db.Grandfather); }
This test gives more details, without exercising all possible code paths of the system. It's still a Facade Test that covers 'just enough' of the integration with underlying components to provide confidence that things work as they should. All the business logic is implemented by a class called MaitreD, which is covered by its own set of targeted unit tests.
While parametrised, this is still only four test cases, so perhaps you don't have sufficient confidence that everything works as it should. Perhaps, as I've outlined in the introductory article, it would help if we converted it to an FsCheck property.
Parametrised property #
I find it safest to refactor this parametrised test to a property in a series of small steps. This implies that I need to keep the [InlineData] attributes around for a while longer, removing one or two literal values at a time, turning them into randomly generated values.
From the previous test we know that the Email and Name values are almost unconstrained. This means that they are trivial in themselves to have FsCheck generate. That change, in itself, is easy, which is good, because combining an [InlineData]-driven [Theory] with an FsCheck property is enough of a mouthful for one refactoring step:
[Theory] [InlineData(1049, 19, 00, 5)] [InlineData(1130, 18, 15, 9)] [InlineData( 956, 16, 55, 2)] [InlineData( 433, 17, 30, 5)] public void PostValidReservationWhenDatabaseIsEmpty( int days, int hours, int minutes, int quantity) { Prop.ForAll( (from r in Gens.Reservation select r).ToArbitrary(), async r => { var at = DateTime.Now.Date + new TimeSpan(days, hours, minutes, 0); var db = new FakeDatabase(); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var expected = r .WithQuantity(quantity) .WithDate(at); await sut.Post(expected.ToDto()); Assert.Contains(expected, db.Grandfather); }).QuickCheckThrowOnFailure(); }
I've now managed to get rid of the email and name parameters, so I've also removed those values from the [InlineData] attributes. Instead, I've asked FsCheck to generate a valid reservation r, which comes with both valid Email and Name.
It turned out that this code base already had some custom generators in a static class called Gens, so I reused those:
internal static Gen<Email> Email => from s in ArbMap.Default.GeneratorFor<NonWhiteSpaceString>() select new Email(s.Item); internal static Gen<Name> Name => from s in ArbMap.Default.GeneratorFor<StringNoNulls>() select new Name(s.Item); internal static Gen<Reservation> Reservation => from id in ArbMap.Default.GeneratorFor<Guid>() from d in ArbMap.Default.GeneratorFor<DateTime>() from e in Email from n in Name from q in ArbMap.Default.GeneratorFor<PositiveInt>() select new Reservation(id, d, e, n, q.Item);
As was also the case with CsCheck you typically use syntactic sugar for monads (which in C# is query syntax) to compose complex test data generators from simpler generators. This enables me to generate an entire Reservation object with a single expression.
Time of day #
Some of the values (such as the reservation's name and email address) that are involved in the PostValidReservationWhenDatabaseIsEmpty test don't really matter. Other values are constrained in some way. Even for the reservation r the above version of the test has to override the arbitrarily generated r value with a specific quantity and a specific at value. This is because you can't just reserve any quantity at any time of day. The restaurant has opening hours and actual tables. Most likely, it doesn't have a table for 100 people at 3 in the morning.
This particular test actually exercises a particular restaurant called Grandfather.Restaurant (because it was the original restaurant that was grandfathered in when the system was expanded to a multi-tenant system). It opens at 16 and has the last seating at 21. This means that the at value has to be between 16 and 21. What's the best way to generate a DateTime value that satisfies this constraint?
You could, naively, ask FsCheck to generate an integer between these two values. You'll see how to do that when we get to the quantity. While that would work for the at value, it would only generate the whole hours 16:00, 17:00, 18:00, etcetera. It would be nice if the test could also exercise times such as 18:30, 20:45, and so on. On the other hand, perhaps we don't want weird reservation times such as 17:09:23.282. How do we tell FsCheck to generate a DateTime value like that?
It's definitely possible to do from scratch, but I chose to do something else. The following shows how test code and production code can co-exist in a symbiotic relationship. The main business logic component that deals with reservations in the system is a class called MaitreD. One of its methods is used to generate a list of time slots for every day. A user interface can use that list to populate a drop-down list of available times. The method is called Segment and can also be used as a data source for an FsCheck test data generator:
internal static Gen<TimeSpan> ReservationTime( Restaurant restaurant, DateTime date) { var slots = restaurant.MaitreD .Segment(date, Enumerable.Empty<Reservation>()) .Select(ts => ts.At.TimeOfDay); return Gen.Elements(slots); }
The Gen.Elements function is an FsCheck combinator that randomly picks a value from a collection. This one, then, picks one of the DataTime values generated by MaitreD.Segment.
The PostValidReservationWhenDatabaseIsEmpty test can now use the ReservationTime generator to produce a time of day:
[Theory] [InlineData(5)] [InlineData(9)] [InlineData(2)] public void PostValidReservationWhenDatabaseIsEmpty(int quantity) { var today = DateTime.Now.Date; Prop.ForAll( (from days in ArbMap.Default.GeneratorFor<PositiveInt>() from t in Gens.ReservationTime(Grandfather.Restaurant, today) let offset = TimeSpan.FromDays((int)days) + t from r in Gens.Reservation select (r, offset)).ToArbitrary(), async t => { var at = today + t.offset; var db = new FakeDatabase(); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(Grandfather.Restaurant), db); var expected = t.r .WithQuantity(quantity) .WithDate(at); await sut.Post(expected.ToDto()); Assert.Contains(expected, db.Grandfather); }).QuickCheckThrowOnFailure(); }
Granted, the test code is getting more and more busy, but there's room for improvement. Before I simplify it, though, I think that it's more prudent to deal with the remaining literal values.
Notice that the InlineData attributes now only supply a single value each: The quantity.
Quantity #
Like the at value, the quantity is constrained. It must be a positive integer, but it can't be larger than the largest table in the restaurant. That number, however, isn't that hard to find:
var maxCapacity = restaurant.MaitreD.Tables.Max(t => t.Capacity);
The FsCheck API includes a function that generates a random number within a given range. It's called Gen.Choose, and now that we know the range, we can use it to generate the quantity value. Here, I'm only showing the test-data-generator part of the test, since the rest doesn't change that much. You'll see the full test again after a few more refactorings.
var today = DateTime.Now.Date; var restaurant = Grandfather.Restaurant; var maxCapacity = restaurant.MaitreD.Tables.Max(t => t.Capacity); Prop.ForAll( (from days in ArbMap.Default.GeneratorFor<PositiveInt>() from t in Gens.ReservationTime(restaurant, today) let offset = TimeSpan.FromDays((int)days) + t from quantity in Gen.Choose(1, maxCapacity) from r in Gens.Reservation select (r.WithQuantity(quantity), offset)).ToArbitrary(),
There are now no more literal values in the test. In a sense, the refactoring from parametrised test to property-based test is complete. It could do with a bit of cleanup, though.
Simplification #
There's no longer any need to pass along the offset variable, and the explicit QuickCheckThrowOnFailure also seems a bit redundant. I can use the [Property] attribute from FsCheck.Xunit instead.
[Property] public Property PostValidReservationWhenDatabaseIsEmpty() { var today = DateTime.Now.Date; var restaurant = Grandfather.Restaurant; var maxCapacity = restaurant.MaitreD.Tables.Max(t => t.Capacity); return Prop.ForAll( (from days in ArbMap.Default.GeneratorFor<PositiveInt>() from t in Gens.ReservationTime(restaurant, today) let at = today + TimeSpan.FromDays((int)days) + t from quantity in Gen.Choose(1, maxCapacity) from r in Gens.Reservation select r.WithQuantity(quantity).WithDate(at)).ToArbitrary(), async expected => { var db = new FakeDatabase(); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(restaurant), db); await sut.Post(expected.ToDto()); Assert.Contains(expected, db.Grandfather); }); }
Compared to the initial version of the test, it has become more top-heavy. It's about the same size, though. The original version was 30 lines of code. This version is only 26 lines of code, but it is admittedly more information-dense. The original version had more 'noise' interleaved with the 'signal'. The new variation actually has a better separation of data generation and the test itself. Consider the 'actual' test code:
var db = new FakeDatabase(); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(restaurant), db); await sut.Post(expected.ToDto()); Assert.Contains(expected, db.Grandfather);
If we could somehow separate the data generation from the test itself, we might have something that was quite readable.
Extract test data generator #
The above data generation consists of a bit of initialisation and a query expression. Like all pure functions it's easy to extract:
private static Gen<(Restaurant, Reservation)> GenValidReservationForEmptyDatabase() { var today = DateTime.Now.Date; var restaurant = Grandfather.Restaurant; var capacity = restaurant.MaitreD.Tables.Max(t => t.Capacity); return from days in ArbMap.Default.GeneratorFor<PositiveInt>() from t in Gens.ReservationTime(restaurant, today) let at = today + TimeSpan.FromDays((int)days) + t from quantity in Gen.Choose(1, capacity) from r in Gens.Reservation select (restaurant, r.WithQuantity(quantity).WithDate(at)); }
While it's quite specialised, it leaves the test itself small and readable:
[Property] public Property PostValidReservationWhenDatabaseIsEmpty() { return Prop.ForAll( GenValidReservationForEmptyDatabase().ToArbitrary(), async t => { var (restaurant, expected) = t; var db = new FakeDatabase(); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(restaurant), db); await sut.Post(expected.ToDto()); Assert.Contains(expected, db[restaurant.Id]); }); }
That's not the only way to separate test and data generation.
Test as implementation detail #
The above separation refactors the data-generating expression to a private helper function. Alternatively you can keep all that FsCheck infrastructure code in the public test method and extract the test body itself to a private helper method:
[Property] public Property PostValidReservationWhenDatabaseIsEmpty() { var today = DateTime.Now.Date; var restaurant = Grandfather.Restaurant; var capacity = restaurant.MaitreD.Tables.Max(t => t.Capacity); var g = from days in ArbMap.Default.GeneratorFor<PositiveInt>() from t in Gens.ReservationTime(restaurant, today) let at = today + TimeSpan.FromDays((int)days) + t from quantity in Gen.Choose(1, capacity) from r in Gens.Reservation select (restaurant, r.WithQuantity(quantity).WithDate(at)); return Prop.ForAll( g.ToArbitrary(), t => PostValidReservationWhenDatabaseIsEmptyImp( t.restaurant, t.Item2)); }
At first glance, that doesn't look like an improvement, but it has the advantage that the actual test method is now devoid of FsCheck details. If we use that as a yardstick for how decoupled the test is from FsCheck, this seems cleaner.
private static async Task PostValidReservationWhenDatabaseIsEmptyImp( Restaurant restaurant, Reservation expected) { var db = new FakeDatabase(); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(restaurant), db); await sut.Post(expected.ToDto()); Assert.Contains(expected, db[restaurant.Id]); }
Using a property-based testing framework in C# is still more awkward than in a language with better support for monadic composition and pattern matching. That said, more recent versions of C# do have better pattern matching on tuples, but this code base is still on C# 8.
If you still think that this looks more complicated than the initial version of the test, then I agree. Property-based testing isn't free, but you get something in return. We started with four test cases and ended with 100. And that's just the default. If you want to increase the number of test cases, that's just an API call away. You could run 1,000 or 10,000 test cases if you wanted to. The only real downside is that the tests take longer to run.
Unhappy paths #
The tests above all test the happy path. A valid request arrives and the system is in a state where it can accept it. This small article series is, you may recall, a response to an email from Sergei Rogovtsev. In his email, he mentioned the need to test both happy path and various error scenarios. Let's cover a few before wrapping up.
As I was developing the system and fleshing out its behaviour, I evolved this parametrised test:
[Theory] [InlineData(null, "j@example.net", "Jay Xerxes", 1)] [InlineData("not a date", "w@example.edu", "Wk Hd", 8)] [InlineData("2023-11-30 20:01", null, "Thora", 19)] [InlineData("2022-01-02 12:10", "3@example.org", "3 Beard", 0)] [InlineData("2045-12-31 11:45", "git@example.com", "Gil Tan", -1)] public async Task PostInvalidReservation( string at, string email, string name, int quantity) { using var api = new LegacyApi(); var response = await api.PostReservation( new { at, email, name, quantity }); Assert.Equal(HttpStatusCode.BadRequest, response.StatusCode); }
The test body itself is about as minimal as it can be. There are four test cases that I added one or two at a time.
- The first test case covers what happens if the
atvalue is missing (i.e. null) - The next test case covers a malformed
atvalue - The third test case covers a missing email address
- The two last test cases covers non-positive quantities, both 0 and a negative number
It's possible to combine FsCheck generators that deal with each of these cases, but here I want to demonstrate how it's still possible to keep each error case separate, if that's what you need. First, separate the test body from its data source, like I did above:
[Theory] [InlineData(null, "j@example.net", "Jay Xerxes", 1)] [InlineData("not a date", "w@example.edu", "Wk Hd", 8)] [InlineData("2023-11-30 20:01", null, "Thora", 19)] [InlineData("2022-01-02 12:10", "3@example.org", "3 Beard", 0)] [InlineData("2045-12-31 11:45", "git@example.com", "Gil Tan", -1)] public async Task PostInvalidReservation( string at, string email, string name, int quantity) { await PostInvalidReservationImp(at, email, name, quantity); } private static async Task PostInvalidReservationImp( string at, string email, string name, int quantity) { using var api = new LegacyApi(); var response = await api.PostReservation( new { at, email, name, quantity }); Assert.Equal(HttpStatusCode.BadRequest, response.StatusCode); }
If you consider this refactoring in isolation, it seems frivolous, but it's just preparation for further work. In each subsequent refactoring I'll convert each of the above error cases to a property.
Missing date and time #
Starting from the top, convert the reservation-at-null test case to a property:
[Property] public async Task PostReservationAtNull(string email, string name, PositiveInt quantity) { await PostInvalidReservationImp(null, email, name, (int)quantity); }
I've left the parametrised PostInvalidReservation test in place, but removed the [InlineData] attribute with the null value for the at parameter:
[Theory] [InlineData("not a date", "w@example.edu", "Wk Hd", 8)] [InlineData("2023-11-30 20:01", null, "Thora", 19)] [InlineData("2022-01-02 12:10", "3@example.org", "3 Beard", 0)] [InlineData("2045-12-31 11:45", "git@example.com", "Gil Tan", -1)] public async Task PostInvalidReservation(
The PostReservationAtNull property can use the FsCheck.Xunit [Property] attribute, because any string can be used for email and name.
To be honest, it is, perhaps, cheating a bit to post any positive quantity, because a number like, say, 1837 would be a problem even if the posted representation was well-formed and valid, since no table of the restaurant has that capacity.
Validation does, however, happen before evaluating business rules and application state, so the way the system is currently implemented, the test never fails because of that. The service never gets to that part of handling the request.
One might argue that this is relying on (and thereby coupling to) an implementation detail, but honestly, it seems unlikely that the service would begin processing an invalid request - 'invalid' implying that the request makes no sense. Concretely, if the date and time is missing from a reservation, how can the service begin to process it? On which date? At what time?
Thus, it's not that likely that this behaviour would change in the future, and therefore unlikely that the test would fail because of a policy change. It is, however, worth considering.
Malformed date and time #
The next error case is when the at value is present, but malformed. You can also convert that case to a property:
[Property] public Property PostMalformedDateAndTime() { var g = from at in ArbMap.Default.GeneratorFor<string>() .Where(s => !DateTime.TryParse(s, out _)) from email in Gens.Email from name in Gens.Name from quantity in Gen.Choose(1, 10) select (at, email: email.ToString(), name: name.ToString(), quantity); return Prop.ForAll( g.ToArbitrary(), t => PostInvalidReservationImp(t.at, t.email, t.name, t.quantity)); }
Given how simple PostReservationAtNull turned out to be, you may be surprised that this case takes so much code to express. There's not that much going on, though. I reuse the generators I already have for email and name, and FsCheck's built-in Gen.Choose to pick a quantity between 1 and 10. The only slightly tricky expression is for the at value.
The distinguishing part of this test is that the at value should be malformed. A randomly generated string is a good starting point. After all, most strings aren't well-formed date-and-time values. Still, a random string could be interpreted as a date or time, so it's better to explicitly disallow such values. This is possible with the Where function. It's a filter that only allows values through that are not understandable as dates or times - which is the vast majority of them.
Null email #
The penultimate error case is when the email address is missing. That one is as easy to express as the missing at value.
[Property] public async Task PostNullEmail(DateTime at, string name, PositiveInt quantity) { await PostInvalidReservationImp(at.ToIso8601DateTimeString(), null, name, (int)quantity); }
Again, with the addition of this specific property, I've removed the corresponding [InlineData] attribute from the PostInvalidReservation test. It only has two remaining test cases, both about non-positive quantities.
Non-positive quantity #
Finally, we can add a property that checks what happens if the quantity isn't positive:
[Property] public async Task PostNonPositiveQuantity( DateTime at, string email, string name, NonNegativeInt quantity) { await PostInvalidReservationImp(at.ToIso8601DateTimeString(), email, name, -(int)quantity); }
FsCheck doesn't have a wrapper for non-positive integers, but I can use NonNegativeInt and negate it. The point is that I want to include 0, which NonNegativeInt does. That wrapper generates integers greater than or equal to zero.
Since I've now modelled each error case as a separate FsCheck property, I can remove the PostInvalidReservation method.
Conclusion #
To be honest, I think that turning these parametrised tests into FsCheck properties is overkill. After all, when I wrote the code base, I found the parametrised tests adequate. I used test-driven development all the way through, and while I also kept the Devil's Advocate in mind, the tests that I wrote gave me sufficient confidence that the system works as it should.
The main point of this article is to show how you can convert example-based tests to property-based tests. After all, just because I felt confident in my test suite it doesn't follow that a few parametrised tests does it for you. How much testing you need depends on a variety of factors, so you may need the extra confidence that thousands of test cases can give you.
The previous article in this series showed an abstract, but minimal example. This one is more realistic, but also more involved.
Next: Refactoring pure function composition without breaking existing tests.
Comments
In the section "Missing date and time", you mention that it could be worth considering the coupling of the test to the implementation details regarding validation order and possible false positive test results. Given that you already have a test data generator that produces valid reservations (GenValidReservationForEmptyDatabase), wouldn't it be more or less trivial to just generate valid test data and modify it to make it invalid in the single specific way you want to test?
Am I right in thinking shrinking doesn't work in FsCheck with the query syntax? I've just tried with two ints. How would you make it work?
[Fact]
public void ShrinkingTest()
{
Prop.ForAll(
(from a1 in Arb.Default.Int32().Generator
from a2 in Arb.Default.Int32().Generator
select (a1, a2)).ToArbitrary(),
t =>
{
if (t.a2 > 10)
throw new System.Exception();
})
.QuickCheckThrowOnFailure();
}Christer, thank you for writing. It wouldn't be impossible to address that concern, but I haven't found a good way of doing it without introducing other problems. So, it's a trade-off.
What I meant by my remark in the article is that in order to make an (otherwise) valid request, the test needs to know the maximum valid quantity, which varies from restaurant to restaurant. The problem, in a nutshell, is that the test in question operates exclusively against the REST API of the service, and that API doesn't expose any functionality that enable clients to query the configuration of tables for a given restaurant. There's no way to obtain that information.
The only two options I can think of are:
- Add such a query API to the REST API. In this case, that seems unwarranted.
- Add a backdoor API to the self-host (
LegacyApi).
If I had to, I'd prefer the second option, but it would still require me to add more (test) code to the code base. There's a cost to every line of code.
Here, I'm making a bet that the grandfathered restaurant isn't going to change its configuration. The tests are then written with the implicit knowledge that that particular restaurant has a maximum table size of 10, and also particular opening and closing times.
This makes those tests more concrete, which makes them more readable. They serve as easy-to-understand examples of how the system works (once the reader has gained the implicit knowledge I just described).
It's not perfect. The tests are, perhaps, too obscure for that reason, and they are vulnerable to configuration changes. Even so, the remedies I can think of come with their own disadvantages.
So far, I've decided that the trade-offs are best leaving things as you see them here. That doesn't mean that I wouldn't change that decision in the future if it turns out that these tests are too brittle.
Anthony, thank you for writing. You're correct that in FsCheck shrinking doesn't work with query syntax; at least in the versions I've used. I'm not sure if that's planned for a future release.
As far as I can tell, this is a consequence of the maturity of the library. You have the same issue with QuickCheck, which also distinguishes between Gen and Arbitrary. While Gen is a monad, Arbitrary's shrink function is invariant, which prevents it from being a functor (and hence, also from being a monad).
FsCheck is a mature port of QuickCheck, so it has the same limitation. No functor, no query syntax.
Later, this limitation was solved by modelling shrinking based on a lazily evaluated shrink tree, which does allow for a monad. The first time I saw that in effect was in Hedgehog.
Hedgehog does a little better than FsCheck but it doesn't shrink well when the variables are dependent.
[Fact]
public void ShrinkingTest_Hedgehog()
{
Property.ForAll(
from a1 in Gen.Int32(Range.ConstantBoundedInt32())
from a2 in Gen.Int32(Range.ConstantBoundedInt32())
where a1 > a2
select (a1, a2))
.Select(t =>
{
if (t.a2 > 10)
throw new System.Exception();
})
.Check(PropertyConfig.Default.WithTests(1_000_000).WithShrinks(1_000_000));
}
[Fact]
public void ShrinkingTest_Hedgehog2()
{
Property.ForAll(
from a1 in Gen.Int32(Range.ConstantBoundedInt32())
from a2 in Gen.Int32(Range.Constant(0, a1))
select (a1, a2))
.Select(t =>
{
if (t.a2 > 10)
throw new System.Exception();
})
.Check(PropertyConfig.Default.WithTests(1_000_000).WithShrinks(1_000_000));
}
[Fact]
public void ShrinkingTest_CsCheck()
{
(from a1 in Gen.Int
from a2 in Gen.Int
where a1 > a2
select (a1, a2))
.Sample((_, a2) =>
{
if (a2 > 10)
throw new Exception();
}, iter: 1_000_000);
}
[Fact]
public void ShrinkingTest_CsCheck2()
{
(from a1 in Gen.Int.Positive
from a2 in Gen.Int[0, a1]
select (a1, a2))
.Sample((_, a2) =>
{
if (a2 > 10)
throw new Exception();
}, iter: 1_000_000);
}This and the syntax complexity I mentioned in the previous post were the reasons I developed CsCheck. Random shrinking is the key innovation that makes it simpler.
Anagrams kata as a one-liner
A futile exercise in code compaction.
Recently I was doing the Anagrams kata in F# with Grzegorz Dziadkiewicz, and along the way realised that the implementation is essentially a one-liner. I thought it would be fun to redo the exercise in Haskell and see how compact code I could get away with.
In short, in the exercise, you're given a list of words, and you need to find all the anagrams in the list. For example, given the list bar, foo, bra, the result should be bar, bra, and foo shouldn't be part of the output, since it's not an anagram of any other word in the list.
A pipeline of transformations #
My idea was to collect all the words in a Map (dictionary) keyed by the string, but sorted. Even if the sorted string is a nonsense word, all anagrams sort to the same sequence of letters:
ghci> sort "bar" "abr" ghci> sort "bra" "abr"
Each of the keys should contain a Set of words, since I don't care about the order.
Once I have that map of sets, I can throw away the singleton sets, and then the keys. Or perhaps first throw away the keys, and then the singleton sets. The order of those two steps doesn't matter.
The reason I don't want the singleton sets is that a set with only one word means that no anagrams were found.
Creating the map #
How to create the desired map? The Map module exports the fromListWith function that enables you to go through an association list and combine values along the way, in case you encounter the key more than once. That sounds useful, but means that first I have to convert the list of words to an association list.
Importing Control.Arrow, I can do it like this:
ghci> fmap (sort &&& Set.singleton) ["bar", "foo", "bra"]
[("abr",fromList ["bar"]),("foo",fromList ["foo"]),("abr",fromList ["bra"])]
Each element in the list is a pair of a key, and a set containing a single word. Notice that the set containing "bar" has the same key as the set containing "bra". When using fromListWith, the function will have to unite these two sets whenever it encounters the same key.
ghci> Map.fromListWith Set.union $ fmap (sort &&& Set.singleton) ["bar", "foo", "bra"]
fromList [("abr",fromList ["bar","bra"]),("foo",fromList ["foo"])]
The two anagrams "bar" and "bra" now belong to the same set, while "foo" is still solitary.
Finding the anagrams #
Now that we've grouped sets according to key, we no longer need the keys:
ghci> Map.elems $ Map.fromListWith Set.union $ fmap (sort &&& Set.singleton) ["bar", "foo", "bra"] [fromList ["bar","bra"],fromList ["foo"]]
The anagrams are those sets that have more than one element, so we can throw away those that are smaller.
ghci> filter ((1 <) . Set.size) $ Map.elems $ Map.fromListWith Set.union $ fmap (sort &&& Set.singleton) ["bar", "foo", "bra"] [fromList ["bar","bra"]]
The expression has now grown to such a width that I've broken it into two lines to make it more readable. It really is just one line, though.
Function #
To save a bit of space, I eta-reduced the expression before I made it a function:
anagrams :: Ord a => [[a]] -> Set (Set [a]) anagrams = Set.fromList . filter ((1 <) . Set.size) . Map.elems . Map.fromListWith Set.union . fmap (sort &&& Set.singleton)
The leftmost Set.fromList converts the list of anagrams to a Set of anagrams, since I didn't think that it was a postcondition that the anagrams should be returned in a specific order.
Unfortunately the expression is still so wide that I found it necessary to break it into two lines.
Just for the hell of it, I tried to fix the situation by changing the imports:
import Control.Arrow import Data.List (sort) import Data.Map.Strict (fromListWith, elems) import Data.Set (Set, fromList, singleton)
With this very specific set of imports, the expression now barely fits on a single line:
anagrams :: Ord a => [[a]] -> Set (Set [a]) anagrams = fromList . filter ((1 <) . length) . elems . fromListWith (<>) . fmap (sort &&& singleton)
Here, I also took advantage of Semigroup append (<>) being equal to Set.union for Set.
Is it readable? Hardly.
My main goal with the exercise was to implement the desired functionality as a single expression. Perhaps I was inspired by Dave Thomas, who wrote:
"I hacked a solution together in 25 lines of Ruby."
25 lines of Ruby? I can do it in one line of Haskell!
Is that interesting? Does it make sense to compare two languages? Why not? By trying out different languages you learn the strengths and weaknesses of each. There's no denying that Haskell is expressive. On the other hand, what you can't see in this blog post is that compilation takes forever. Not for this code in particular, but in general.
I'm sure Dave Thomas was done with his Ruby implementation before my machine had even finished compiling the empty, scaffolded Haskell code.
Performance #
Dave Thomas also wrote:
"It runs on this wordlist in 1.8s on a 1.7GHz i7."
Usually I don't care that much about performance as long as it's adequate. Or rather, I find that good software architecture with poor algorithms usually beats bad architecture with good algorithms. But I digress.
How fares my one-liner against Dave Thomas' implementation?
ghci> :set +s ghci> length . anagrams . lines <$> readFile "wordlist.txt" 20683 (3.56 secs, 1,749,984,448 bytes)
Oh, 3.56 seconds isn't particularly g Holy thunk, Batman! 1.7 gigabytes!
That's actually disappointing, I admit. If only I could excuse this by running on a weaker machine, but mine is a 1.9 GHz i7. Nominally faster than Dave Thomas' machine.
At least, the time it takes to run through that 3.7 MB file is the same order of magnitude.
Tests #
Since I had a good idea about the kind of implementation I was aiming for, I didn't write that many tests. Only three, actually.
main :: IO () main = defaultMain $ hUnitTestToTests (TestList [ "Examples" ~: do (words, expected) <- [ (["foo", "bar", "baz"], Set.empty), (["bar", "foo", "bra"], Set.fromList [Set.fromList ["bar", "bra"]]), (["foo", "bar", "bra", "oof"], Set.fromList [ Set.fromList ["foo", "oof"], Set.fromList ["bar", "bra"]]) ] let actual = anagrams words return $ expected ~=? actual ])
As I usually do it in Haskell, these are inlined parametrised HUnit tests.
Conclusion #
Doing katas is a good way to try out new ideas, dumb or otherwise. Implementing the Anagrams kata as a one-liner was fun, but the final code shown here is sufficiently unreadable that I wouldn't recommend it.
You could still write the anagrams function based on the idea presented here, but in a shared code base with an indefinite life span, I'd break it up into multiple expressions with descriptive names.
An abstract example of refactoring from interaction-based to property-based testing
A C# example with xUnit.net and CsCheck
This is the first comprehensive example that accompanies the article Epistemology of interaction testing. In that article, I argue that in a code base that leans toward functional programming (FP), property-based testing is a better fit than interaction-based testing. In this example, I will show how to refactor simple interaction-based tests into a property-based tests.
This small article series was prompted by an email from Sergei Rogovtsev, who was kind enough to furnish example code. I'll use his code as a starting point for this example, so I've forked the repository. If you want to follow along, all my work is in a branch called no-mocks. That branch simply continues off the master branch.
Interaction-based testing #
Sergei Rogovtsev writes:
"A major thing to point out here is that I'm not following TDD here not by my own choice, but because my original question arose in a context of a legacy system devoid of tests, so I choose to present it to you in the same way. I imagine that working from tests would avoid a lot of questions."
Even when using test-driven development (TDD), most code bases I've seen make use of Stubs and Mocks (or, rather, Spies). In an object-oriented context this can make much sense. After all, a catch phrase of object-oriented programming is tell, don't ask.
If you base API design on that principle, you're modelling side effects, and it makes sense that tests use Spies to verify those side effects. The book Growing Object-Oriented Software, Guided by Tests is a good example of this approach. Thus, even if you follow established good TDD practice, you could easily arrive at a code base reminiscent of Sergei Rogovtsev's example. I've written plenty of such code bases myself.
Sergei Rogovtsev then extracts a couple of components, leaving him with a Controller class looking like this:
public string Complete(string state, string code) { var knownState = _repository.GetState(state); try { if (_stateValidator.Validate(code, knownState)) return _renderer.Success(knownState); else return _renderer.Failure(knownState); } catch (Exception e) { return _renderer.Error(knownState, e); } }
This code snippet doesn't show the entire class, but only its solitary action method. Keep in mind that the entire repository is available on GitHub if you want to see the surrounding code.
The Complete method orchestrates three injected dependencies: _repository, _stateValidator, and _renderer. The question that Sergei Rogovtsev asks is how to test this method. You may think that it's so simple that you don't need to test it, but keep in mind that this is a minimal and self-contained example that stands in for something more complicated.
The method has a cyclomatic complexity of 3, so you need at least three test cases. That's also what Sergei Rogovtsev's code contains. I'll show each test case in turn, while I refactor them.
The overall question is still this: Both IStateValidator and IRenderer interfaces have only a single production implementation, and in both cases the implementations are pure functions. If interaction-based testing is suboptimal, is there a better way to test this code?
As I outlined in the introductory article, I consider property-based testing a good alternative. In the following, I'll refactor the tests. Since the tests already use AutoFixture, most of the preliminary work can be done without choosing a property-based testing framework. I'll postpone that decision until I need it.
State validator #
The IStateValidator interface has a single implementation:
public class StateValidator : IStateValidator { public bool Validate(string code, (string expectedCode, bool isMobile, Uri redirect) knownState) => code == knownState.expectedCode; }
The Validate method is a pure function, so it's completely deterministic. It means that you don't have to hide it behind an interface and replace it with a Test Double in order to control it. Rather, just feed it proper data. Still, that's not what the interaction-based tests do:
[Theory] [AutoData] public void HappyPath(string state, string code, (string, bool, Uri) knownState, string response) { _repository.Add(state, knownState); _stateValidator .Setup(validator => validator.Validate(code, knownState)) .Returns(true); _renderer .Setup(renderer => renderer.Success(knownState)) .Returns(response); _target .Complete(state, code) .Should().Be(response); }
These tests use AutoFixture, which will make it a bit easier to refactor them to properties. It also makes the test a bit more abstract, since you don't get to see concrete test data. In short, the [AutoData] attribute will generate a random state string, a random code string, and so on. If you want to see an example with concrete test data, the next article shows that variation.
The test uses Moq to control the behaviour of the Test Doubles. It states that the Validate method will return true when called with certain arguments. This is possible because you can redefine its behaviour, but as far as executable specifications go, this test doesn't reflect reality. There's only one Validate implementation, and it doesn't behave like that. Rather, it'll return true when code is equal to knownState.expectedCode. The test poorly communicates that behaviour.
Even before I replace AutoFixture with CsCheck, I'll prepare the test by making it more honest. I'll replace the code parameter with a Derived Value:
[Theory] [AutoData] public void HappyPath(string state, (string, bool, Uri) knownState, string response) { var (expectedCode, _, _) = knownState; var code = expectedCode; // The rest of the test...
I've removed the code parameter to replace it with a variable derived from knownState. Notice how this documents the overall behaviour of the (sub-)system.
This also means that I can now replace the IStateValidator Test Double with the real, pure implementation:
[Theory] [AutoData] public void HappyPath(string state, (string, bool, Uri) knownState, string response) { var (expectedCode, _, _) = knownState; var code = expectedCode; _repository.Add(state, knownState); _renderer .Setup(renderer => renderer.Success(knownState)) .Returns(response); var sut = new Controller(_repository, new StateValidator(), _renderer.Object); sut .Complete(state, code) .Should().Be(response); }
I give the Failure test case the same treatment:
[Theory] [AutoData] public void Failure(string state, (string, bool, Uri) knownState, string response) { var (expectedCode, _, _) = knownState; var code = expectedCode + "1"; // Any extra string will do _repository.Add(state, knownState); _renderer .Setup(renderer => renderer.Failure(knownState)) .Returns(response); var sut = new Controller(_repository, new StateValidator(), _renderer.Object); sut .Complete(state, code) .Should().Be(response); }
The third test case is a bit more interesting.
An impossible case #
Before I make any changes to it, the third test case is this:
[Theory] [AutoData] public void Error( string state, string code, (string, bool, Uri) knownState, Exception e, string response) { _repository.Add(state, knownState); _stateValidator .Setup(validator => validator.Validate(code, knownState)) .Throws(e); _renderer .Setup(renderer => renderer.Error(knownState, e)) .Returns(response); _target .Complete(state, code) .Should().Be(response); }
This test case verifies the behaviour of the Controller class when the Validate method throws an exception. If we want to instead use the real, pure implementation, how can we get it to throw an exception? Consider it again:
public bool Validate(string code, (string expectedCode, bool isMobile, Uri redirect) knownState) => code == knownState.expectedCode;
As far as I can tell, there's no way to get this method to throw an exception. You might suggest passing null as the knownState parameter, but that's not possible. This is a new version of C# and the nullable reference types feature is turned on. I spent some fifteen minutes trying to convince the compiler to pass a null argument in place of knownState, but I couldn't make it work in a unit test.
That's interesting. The Error test is exercising a code path that's impossible in production. Is it redundant?
It might be, but here I think that it's more an artefact of the process. Sergei Rogovtsev has provided a minimal example, and as it sometimes happens, perhaps it's a bit too minimal. He did write, however, that he considered it essential for the example that the logic involved more that an Boolean true/false condition. In order to keep with the spirit of the example, then, I'm going to modify the Validate method so that it's also possible to make it throw an exception:
public bool Validate(string code, (string expectedCode, bool isMobile, Uri redirect) knownState) { if (knownState == default) throw new ArgumentNullException(nameof(knownState)); return code == knownState.expectedCode; }
The method now throws an exception if you pass it a default value for knownState. From an implementation standpoint, there's no reason to do this, so it's only for the sake of the example. You can now test how the Controller handles an exception:
[Theory] [AutoData] public void Error(string state, string code, string response) { _repository.Add(state, default); _renderer .Setup(renderer => renderer.Error(default, It.IsAny<Exception>())) .Returns(response); var sut = new Controller(_repository, new StateValidator(), _renderer.Object); sut .Complete(state, code) .Should().Be(response); }
The test no longer has a reference to the specific Exception object that Validate is going to throw, so instead it has to use Moq's It.IsAny API to configure the _renderer. This is, however, only an interim step, since it's now time to treat that dependency in the same way as the validator.
Renderer #
The Renderer class has three methods, and they are all pure functions:
public class Renderer : IRenderer { public string Success((string expectedCode, bool isMobile, Uri redirect) knownState) { if (knownState.isMobile) return "{\"success\": true, \"redirect\": \"" + knownState.redirect + "\"}"; else return "302 Location: " + knownState.redirect; } public string Failure((string expectedCode, bool isMobile, Uri redirect) knownState) { if (knownState.isMobile) return "{\"success\": false, \"redirect\": \"login\"}"; else return "302 Location: login"; } public string Error((string expectedCode, bool isMobile, Uri redirect) knownState, Exception e) { if (knownState.isMobile) return "{\"error\": \"" + e.Message + "\"}"; else return "500"; } }
Since all three methods are deterministic, automated tests can control their behaviour simply by passing in the appropriate arguments:
[Theory] [AutoData] public void HappyPath(string state, (string, bool, Uri) knownState, string response) { var (expectedCode, _, _) = knownState; var code = expectedCode; _repository.Add(state, knownState); var renderer = new Renderer(); var sut = new Controller(_repository, renderer); var expected = renderer.Success(knownState); sut .Complete(state, code) .Should().Be(expected); }
Instead of configuring an IRenderer Stub, the test can state the expected output: That the output is equal to the output that renderer.Success would return.
Notice that the test doesn't require that the implementation calls renderer.Success. It only requires that the output is equal to the output that renderer.Success would return. Thus, it has less of an opinion about the implementation, which means that it's marginally less coupled to it.
You might protest that the test now duplicates the implementation code. This is partially true, but no more than the previous incarnation of it. Before, the test used Moq to explicitly require that renderer.Success gets called. Now, there's still coupling, but this refactoring reduces it.
As a side note, this may partially be an artefact of the process. Here I'm refactoring tests while keeping the implementation intact. Had I started with a property, perhaps the test would have turned out differently, and less coupled to the implementation. If you're interested in a successful exercise in using property-based TDD, you may find my article Property-based testing is not the same as partition testing interesting.
Simplification #
Once you've refactored the tests to use the pure functions as dependencies, you no longer need the interfaces. The interfaces IStateValidator and IRenderer only existed to support testing. Now that the tests no longer use the interfaces, you can delete them.
Furthermore, once you've removed those interfaces, there's no reason for the classes to support instantiation. Instead, make them static:
public static class StateValidator { public static bool Validate( string code, (string expectedCode, bool isMobile, Uri redirect) knownState) { if (knownState == default) throw new ArgumentNullException(nameof(knownState)); return code == knownState.expectedCode; } }
You can do the same for the Renderer class.
This doesn't change the overall flow of the Controller class' Complete method, although the implementation details have changed a bit:
public string Complete(string state, string code) { var knownState = _repository.GetState(state); try { if (StateValidator.Validate(code, knownState)) return Renderer.Success(knownState); else return Renderer.Failure(knownState); } catch (Exception e) { return Renderer.Error(knownState, e); } }
StateValidator and Renderer are no longer injected dependencies, but rather 'modules' that affords pure functions.
Both the Controller class and the tests that cover it are simpler.
Properties #
So far I've been able to make all these changes without introducing a property-based testing framework. This was possible because the tests already used AutoFixture, which, while not a property-based testing framework, already strongly encourages you to write tests without literal test data.
This makes it easy to make the final change to property-based testing. On the other hand, it's a bit unfortunate from a pedagogical perspective. This means that you didn't get to see how to refactor a 'traditional' unit test to a property. The next article in this series will plug that hole, as well as show a more realistic example.
It's now time to pick a property-based testing framework. On .NET you have a few choices. Since this code base is C#, you may consider a framework written in C#. I'm not convinced that this is necessarily better, but it's a worthwhile experiment. Here I've used CsCheck.
Since the tests already used randomly generated test data, the conversion to CsCheck is relatively straightforward. I'm only going to show one of the tests. You can always find the rest of the code in the Git repository.
[Fact] public void HappyPath() { (from state in Gen.String from expectedCode in Gen.String from isMobile in Gen.Bool let urls = new[] { "https://example.com", "https://example.org" } from redirect in Gen.OneOfConst(urls).Select(s => new Uri(s)) select (state, (expectedCode, isMobile, redirect))) .Sample((state, knownState) => { var (expectedCode, _, _) = knownState; var code = expectedCode; var repository = new RepositoryStub(); repository.Add(state, knownState); var sut = new Controller(repository); var expected = Renderer.Success(knownState); sut .Complete(state, code) .Should().Be(expected); }); }
Compared to the AutoFixture version of the test, this looks more complicated. Part of it is that CsCheck (as far as I know) doesn't have the same integration with xUnit.net that AutoFixture has. That might be an issue that someone could address; after all, FsCheck has framework integration, to name an example.
Test data generators are monads so you typically leverage whatever syntactic sugar a language offers to simplify monadic composition. In C# that syntactic sugar is query syntax, which explains that initial from block.
The test does look too top-heavy for my taste. An equivalent problem appears in the next article, where I also try to address it. In general, the better monad support a language offers, the more elegantly you can address this kind of problem. C# isn't really there yet, whereas languages like F# and Haskell offer superior alternatives.
Conclusion #
In this article I've tried to demonstrate how property-based testing is a viable alternative to using Stubs and Mocks for verification of composition. You can try to sabotage the Controller.Complete method in the no-mocks branch and see that one or more properties will fail.
While the example code base that I've used for this article has the strength of being small and self-contained, it also suffers from a few weaknesses. It's perhaps a bit too abstract to truly resonate. It also uses AutoFixture to generate test data, which already takes it halfway towards property-based testing. While that makes the refactoring easier, it also means that it may not fully demonstrate how to refactor an example-based test to a property. I'll try to address these shortcomings in the next article.
Next: A restaurant example of refactoring from example-based to property-based testing.
Comments
First of all, thanks again for continuing to explore this matter. This was very enlightening, but in the end, I was left with is a sense of subtle wrongness, which is very hard to pin down, and even harder to tell apart between "this is actually not right for me" and "this is something new I'm not accustomed to".
I suppose that my main question would center around difference between your tests for IStateValidator and IRenderer. Let's start with the latter:
Instead of configuring an
IRendererStub, the test can state the expected output: That the output is equal to the output thatrenderer.Successwould return.
Coupled with the explanation ("[the test] has less of an opinion about the implementation, which means that it's marginally less coupled to it"), this makes a lot of sense, with the only caveat that in more production-like cases comparing the output would be harder (e.g., if IRenderer operates on HttpContext to produce a full HTTP response), but that's a technicality that can be sorted out with proper assertion library. But let's now look at the IStateValidator part:
as far as executable specifications go, this test doesn't reflect reality. There's only one
Validateimplementation, and it doesn't behave like that. Rather, it'll return true when code is equal toknownState.expectedCode. The test poorly communicates that behaviour.
Here you act with the opposite intent: you want the test to communicate the specification, and thus be explicitly tied to the logic in the implementation (if not the actual code of it). There are two thing about that that bother me. First of all, it's somewhat inconsistent, so it makes it harder for me to choose which path to follow when testing the next code I'd write (or articulating to another developer how they should do it). But what's more important - and that comes from my example being minimal, as you've already noted - is that the validation logic might be more complicated, and thus the setup would be complicated as well. And as you've already mentioned on Twitter, when chaging the code in the validator implementation, you might be forced to change the implementation in the test, even if the test is more about the controller itself.
There's also another frame for the same issue: the original test read as (at least for me): "if the state is valid, we return successful response based on this state". It didn't matter what is "valid" not did it matter what is "successful response". The new tests reads as "if state in the repository matches passed code, we return successful response for the state". It still doesn't matter what is "successful response", but the definition of validity does matter. For me, this is a change of test meaning, and I'm not sure I understand where that leads me.
Let's consider the following scenario: we need to add another validity criteria, such as "state in repository has an expiration date, and this date should be in the future". We obviously need to add a couple of tests for this (negative and positive). Where do we add them? I'd say we add them into the tests for the validator itself (which are "not shown" for the purposes of brevity), but then it feels weird that we also need to change this "happy path" test...
Thanks for showing CsCheck. I've put in a PR to show how I would refactor the CsCheck tests and will attempt to explain some of the design choices of CsCheck.
First of all, it may be a personal opinion but I don't really tend to use query syntax for CsCheck. I prefer to see the SelectManys and there are a number of additional overloads that simplify ranging and composing Gens.
On the design of CsCheck, I build it to not use reflection, attributes or target test frameworks. I've seen the very difficult problems these lead to (for author and user) when you try to move past simple examples.
I wanted the user to be able to move from simple general type generators to ranged complex types easily in a fluent style. No Arbs, attributes, PositiveInt type etc.
CsCheck has automatic shrinking even for the most complex types that just comes out of composing Gens.
I think some of the reason it was so easy to extend the library to areas such as concurrency testing was because of this simplicity (as well as the random shrinking insight).
Gen<Uri> _genRedirect = Gen.OneOfConst(new Uri("https://example.com"), new Uri("https://example.org"));
[Fact]
public void HappyPath()
{
Gen.Select(Gen.String, Gen.String, Gen.Bool, _genRedirect)
.Sample((state, expectedCode, isMobile, redirect) =>
{
var code = expectedCode;
var knownState = (expectedCode, isMobile, redirect);
var repository = new RepositoryStub { { state, knownState } };
var sut = new Controller(repository);
var actual = sut.Complete(state, code);
var expected = Renderer.Success(knownState);
return actual == expected;
});
}Sergei, thank you for writing. I'm afraid all of this is context-dependent, and I seem to constantly fail giving enough context. It's a fair criticism that I seem to employ inconsistent heuristics when making technical decisions. Part of it is caused by my lack of context. The code base is deliberately stripped of context, which has many other benefits, but gives me little to navigate after. I'm flying blind, so to speak. I've had to (implicitly) imagine some forces acting on the software in order to make technical decisions. Since we haven't explicitly outlined such forces, I've had to make them up as I went. It's quite possible, even, that I've imagined one set of forces in one place, and another set somewhere else. If so, no wonder the decisions are inconsistent.
What do I mean by forces? I'm thinking of the surrounding context that you have to take into a account when making technical decisions about code: Is the current feature urgent? Is it a bug already in production? Is this a new system with a small code base? Or is it an old system with a large code base? Do you have good automated tests? Do you have a Continuous Delivery pipeline? Are you experiencing problems with code quality? What does the team makeup look like? Do you have mostly seasoned veterans who've worked in that code base for years? Or do you have many newcomers? Is the system public-facing or internal? Is it a system, even, or a library or framework? What sort of organisation owns the software? Is it a product group? Or a cost centre? What is the organization's goals? How are you incentivized? How are other stakeholders incentivized?
As you can imagine, I can keep going, asking questions like these, and they may all be relevant. Clearly, we can't expect a self-contained minimal example to also include all such superstructure, so that's what I (inconsistently) have to imagine, on the fly.
I admit that the decisions I describe seem inconsistent, and the explanation may simply be what is already implied above: I may have had a different context in mind when I made one, and a variation in mind when I made the other.
That's hardly the whole story, though. I didn't start my answer with the above litany of forces only to make a bad excuse for myself. Rather, what I had in mind was to argue that I use a wider context when making decisions. That context is not just technical, but includes, among many other considerations, the team structure.
As an example, I was recently working with some students in a university setting. These are people in their early twenties, with only a few months of academic programming under their belt, as well as, perhaps, a few years of hobby programming. They'd just been introduced to Git and GitHub a few weeks earlier, C# a month before that. I was trying to teach them how to use Git and GitHub, how to structure decent C# code, and many other things. During our project, they did send me a few pull requests I would have immediately rejected from a professional programmer. In this particular context, however, that would have been counter-productive. These students were doing a good job, based on their level of experience, and they needed the sense of accomplishment that I would (often, but not always) accept their code.
I could have insisted on a higher code quality, and I would also have been able to teach it to anyone patient enough to listen. One thing I've learned all too slowly in my decades of working with other people is that most people aren't as patient with me as I'd like them to be. I need to explicitly consider how to motivate my collaborators.
Here's another example: Years ago, I worked with a rag-tag team hastily assembled via word-of-mouth of some fine European freelancers. My challenge here was another. These people were used to be on top of their game - usually the ones brought in to an organisation because they were the best. I needed them to work together, and among other things, it meant showing them that even though they might think that their way was the best way, other ways exist. I wanted them to be able to work together and produce code with shared ownership. At the beginning, I was rather strict with my standards, clearly bruising a few egos, but ultimately several members have told what a positive transformative experience it was for them. It was a positive transformative experience for me, too.
I discuss all of this because you, among various points, mention the need to be able to articulate to other developers how to make technical decisions about tests. The point is that there's a lot of context that goes into making decisions, and hardly a one-size-fits-all heuristic.
What usually guides me is an emphasis on coupling, and that's also, I believe, what ultimately motivated me here. There's always going to be some coupling between tests and production code, but the less the better. For example, when considering whether how to write an assertion, I consider whether a change in production code's behaviour would cause a test to break.
Consider, for example, the renderer in the present example. How important is the exact output? What happens if I change a character in the string that is being returned?
That's a good example of context being important. If that output is part of an implementation of a network protocol or some other technical spec, just one character change could, indeed, imply that your implementation is off spec. In that case, we do want to test the exact output, and we do want the test to fail if the output changes.
On the other hand, if the output is a piece of UI, or perhaps an error message, then the exact wording is likely to change over time. Since this doesn't really imply a change in behaviour, changing such a string output shouldn't break a test.
You need that wider context in order to make decisions like that: If we change the System Under Test in this way, will the test break? Should it? What if we change it in another way?
This is relevant in order to address your final concern: What if you now decide that the expiration date should be in the future? The way you describe it, it sounds like this strengthens the preconditions of the system - in other words, it breaks backwards compatibility. So yes, making that change may break existing tests, but this could be an indication that it's also going to break existing clients.
If you have any clients, that is. Again, you know your context better than I do, so only you can decide whether making such a change is okay. I can think of situations where is, but I usually find myself in contexts where it isn't, so I tend to err on the side of avoiding breaking changes.
Mark, thank you for taking the time to discuss this.
Having the magic word "architect" somewhere in my title, I know the importance of context, and in fact that would usually be the first counter-question that I have for somebody coming at me with a question: "what is your context?". So here we are, me being contractually obliged to strip as much context from my code as possible, and you having to reinvent it back from your experience. On the other hand, this allows us to point out which decisions are actually context-driven, and how different contexts affect them.
With that in mind, I can actually propose two different contexts to reframe the decisions above, so that we could arrive at more insights.
The first would be an imaginary context, which I had in mind when writing the code, but haven't thought of communicating: the renderer is as important as the validator. In case of "mobile" state the consumer is actually a mobile application, so we need to know we've produced the right JSON it will consume, and in case of non-"mobile" state the consumer is the browser, which again needs to be properly redirected. In my mind, this is no less important than the validation logic itself, because breaking it will break at least one consumer (mobile), and more likely both of them. Thus, according to the logic above, this is a compatibility issue, and as such we need to explicitly spell this behavior in the tests. Which gives us six outcome branches... six tests? Or something more complicated? This is especially interesting, considering the fact that we can test the renderer in isolation, so we'd be either duplicating our tests... or just just discarding the isolated tests for the renderer?
And then here's the actual real context, which I can thankfully divulge to this extent: this is, in fact, a migration problem, when we move from one externally-facing framework (i.e. ASP.NET Web API) to another (i.e. ASP.NET Core). So I am not, in fact, concerned about the validation at all - I'm concerned about the data being properly passed to the validator (because the validator already existed, and worked properly, I'm just calling it from another framework), its result properly handled in the controller (which I am replacing), and then I'm concerned that despite the heavy changes between ASP.NET versions I'm still rendering the output in the exactly same way.
Now that I'm thinking about it, it seems grossly unfair that I've hidden this context beforehand, but then, I didn't see how it was affecting the decisions in test design. So hopefully we can still find some use in this.
Anthony, thank you for writing. I didn't intend to disparage CsCheck. Having once run a moderately successful open source project, I've learned that it's a good idea to limit the scope to a functional minimum. I'm not complaining about the design decisions made for CsCheck.
I was a bit concerned that a casual reader might compare the CsCheck example with the previous code and be put off by the apparent complexity. I admit that your example looks less complex than mine, so to address that particular concern, I could have used code similar to yours.
Whether one prefers the syntactic sugar of query syntax or the more explicit use of SelectMany is, to a degree, subjective. There are, on the other hand, some cases where one is objectively better than the other. One day I should write an article about that.
I agree that the test-framework integration that exists in FsCheck is less than ideal. I'm not wishing for anything like that. Something declarative, however, would be nice. Contrary to you, I consider wrapper types like PositiveInt to be a boon, but perhaps not like they're implemented in FsCheck. (And this, by the way, isn't to harp on FsCheck either; I only bring up those examples because FsCheck has more of that kind of API than Hedgehog does.) The Haskell QuickCheck approach is nice: While a wrapper like Positive is predefined in the package, it's just an Arbitrary instance. There's really nothing special about it, and you can easily define domain-specific wrappers for your own testing purposes. Here's an example: Naming newtypes for QuickCheck Arbitraries. I'm wondering if something similar wouldn't be possible with interfaces in .NET.
Sergei, thank you for writing. I'm sorry if I came across as condescending or implying that you weren't aware that context matters. Of course you do. I was mostly trying to reconstruct my own decision process, which is far less explicit than you might like.
Regarding the renderer component, I understand that testing such a thing in reality may be more involved than the toy example we're looking at. My first concern is to avoid duplicating efforts too much. Again, however, the external behaviour should be the primary concern. I'm increasingly shifting towards making more and more things internal, as long as I can still test them via the application boundary. As I understand it, this is the same concern that made Dan North come up with behaviour-driven development. I'm also concerned primarily with testing the behaviour of systems, just without all the Gherkin overhead.
There comes a time, however, where testing everything through an external API becomes too awkward. I'm not adverse to introduce or make public classes or functions to enable testing at a different abstraction level. Doing that, however, represents a bet that it's possible to keep the new component's API stable enough that it isn't going to cause too much test churn. Still, if we imagine that we've already made such a decision, and that we now have some renderer component, then it's only natural to test it thoroughly. Then, in order to avoid duplicating assertions, we can state, as I did in this article, that the overall system should expect to see whatever the renderer component returns.
That was, perhaps, too wordy an explanation. Perhaps this is more helpful: Don't repeat yourself. What has been asserted in one place shouldn't be asserted in another place.
The other example you mention, about migrating to another framework, reminds me of two things.
The first is that we shouldn't forget about other ways of verifying code correctness. We've mostly been discussing black-box testing, and while it can be an interesting exercise to imagine an adversary developer, in general that's rarely the reality. Are there other ways to verify that methods are called with the correct values? How about looking at the code? Consistent code reviews are good at detecting bugs.
The second observation is that if you already have two working components (validator and renderer) you can treat them as Test Oracles. This still works well with property-based testing. Write tests based on equivalence classes and get a property-based testing framework to sample from those classes. Then use the Test Oracles to define the expected output. That's essentially what I have done in this article.
Does it prove that your framework-based code calls the components with the correct arguments? No, not like if you'd used a Test Spy. Property-based testing produces knowledge reminiscent of the kind of knowledge produced by experimental physics; not the kind of axiomatic knowledge produced by mathematics. That's why I named this article series Epistemology of interaction testing.
Is it wrong to test with Stubs or Spies in a case like this? Not necessarily. Ultimately, what I try to do with this blog is to investigate and present alternatives. Only once we have alternatives do we have choices.

Comments
Seems like a useful function to have, so I naturally wondered if I could
make it worseimplement a similar function in Emacs.Emacs lisp has support for regular expressions, only typically with a bunch of extra slashes included, so I needed to figure out how to work with the currently selected text to get this to work. The currently selected text is referred to as the "region" and by specifying
"r"as a parameter for theinteractivecall we can pass the start and end positions for the region directly to the function.I came up with this rather basic function:
(defun make-url-relative (start end) "Converts the selected uri from an absolute url and converts it to a relative one. This is very simple and relies on the url starting with http/https, and removes each character to the first slash in the path" (interactive "r") (replace-regexp-in-region "http[s?]:\/\/.+\/" "" start end))With this function included in config somewhere: it can be called by selecting a url, and using M-x
make-url-relative(or assigned to a key binding as required)I'm not sure if there's an already existing package for this functionality, but I hadn't really thought to look for it before so thanks for the idea 😊