ploeh blog danish software design
Trimming a Fake Object
A refactoring example.
When I introduce the Fake Object testing pattern to people, a common concern is the maintenance burden of it. The point of the pattern is that you write some 'working' code only for test purposes. At a glance, it seems as though it'd be more work than using a dynamic mock library like Moq or Mockito.
This article isn't really about that, but the benefit of a Fake Object is that it has a lower maintenance footprint because it gives you a single class to maintain when you change interfaces or base classes. Dynamic mock objects, on the contrary, leads to Shotgun surgery because every time you change an interface or base class, you have to revisit multiple tests.
In a recent article I presented a Fake Object that may have looked bigger than most people would find comfortable for test code. In this article I discuss how to trim it via a set of refactorings.
Original Fake read registry #
The article presented this FakeReadRegistry, repeated here for your convenience:
internal sealed class FakeReadRegistry : IReadRegistry { private readonly IReadOnlyCollection<Room> rooms; private readonly IDictionary<DateOnly, IReadOnlyCollection<Room>> views; public FakeReadRegistry(params Room[] rooms) { this.rooms = rooms; views = new Dictionary<DateOnly, IReadOnlyCollection<Room>>(); } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return EnumerateDates(arrival, departure) .Select(GetView) .Aggregate(rooms.AsEnumerable(), Enumerable.Intersect) .ToList(); } public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = QueryService.Reserve(booking, view); views[d] = newView; } } private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } } private IReadOnlyCollection<Room> GetView(DateOnly date) { if (views.TryGetValue(date, out var view)) return view; else return rooms; } }
This is 47 lines of code, spread over five members (including the constructor). Three of the methods have a cyclomatic complexity (CC) of 2, which is the maximum for this class. The remaining two have a CC of 1.
While you can play some CC golf with those CC-2 methods, that tends to pull the code in a direction of being less idiomatic. For that reason, I chose to present the code as above. Perhaps more importantly, it doesn't save that many lines of code.
Had this been a piece of production code, no-one would bat an eye at size or complexity, but this is test code. To add spite to injury, those 47 lines of code implement this two-method interface:
public interface IReadRegistry { IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure); void RoomBooked(Booking booking); }
Can we improve the situation?
Root cause analysis #
Before you rush to 'improve' code, it pays to understand why it looks the way it looks.
Code is a wonderfully malleable medium, so you should regard nothing as set in stone. On the other hand, there's often a reason it looks like it does. It may be that the previous programmers were incompetent ogres for hire, but often there's a better explanation.
I've outlined my thinking process in the previous article, and I'm not going to repeat it all here. To summarise, though, I've applied the Dependency Inversion Principle.
"clients [...] own the abstract interfaces"
In other words, I let the needs of the clients guide the design of the IReadRegistry interface, and then the implementation (FakeReadRegistry) had to conform.
But that's not the whole truth.
I was doing a programming exercise - the CQRS booking kata - and I was following the instructions given in the description. They quite explicitly outline the two dependencies and their methods.
When trying a new exercise, it's a good idea to follow instructions closely, so that's what I did. Once you get a sense of a kata, though, there's no law saying that you have to stick to the original rules. After all, the purpose of an exercise is to train, and in programming, trying new things is training.
Test code that wants to be production code #
A major benefit of test-driven development (TDD) is that it provides feedback. It pays to be tuned in to that channel. The above FakeReadRegistry seems to be trying to tell us something.
Consider the GetFreeRooms method. I'll repeat the single-expression body here for your convenience:
return EnumerateDates(arrival, departure)
.Select(GetView)
.Aggregate(rooms.AsEnumerable(), Enumerable.Intersect)
.ToList();
Why is that the implementation? Why does it need to first enumerate the dates in the requested interval? Why does it need to call GetView for each date?
Why don't I just do the following and be done with it?
internal sealed class FakeStorage : Collection<Booking>, IWriteRegistry, IReadRegistry { private readonly IReadOnlyCollection<Room> rooms; public FakeStorage(params Room[] rooms) { this.rooms = rooms; } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { var booked = this.Where(b => b.Overlaps(arrival, departure)).ToList(); return rooms .Where(r => !booked.Any(b => b.RoomName == r.Name)) .ToList(); } public void Save(Booking booking) { Add(booking); } }
To be honest, that's what I did first.
While there are two interfaces, there's only one Fake Object implementing both. That's often an easy way to address the Interface Segregation Principle and still keeping the Fake Object simple.
This is much simpler than FakeReadRegistry, so why didn't I just keep that?
I didn't feel it was an honest attempt at CQRS. In CQRS you typically write the data changes to one system, and then you have another logical process that propagates the information about the data modification to the read subsystem. There's none of that here. Instead of being based on one or more 'materialised views', the query is just that: A query.
That was what I attempted to address with FakeReadRegistry, and I think it's a much more faithful CQRS implementation. It's also more complex, as CQRS tends to be.
In both cases, however, it seems that there's some production logic trapped in the test code. Shouldn't EnumerateDates be production code? And how about the general 'algorithm' of RoomBooked:
- Enumerate the relevant dates
- Get the 'materialised' view for each date
- Calculate the new view for that date
- Update the collection of views for that date
That seems like just enough code to warrant moving it to the production code.
A word of caution before we proceed. When deciding to pull some of that test code into the production code, I'm making a decision about architecture.
Until now, I'd been following the Dependency Inversion Principle closely. The interfaces exist because the client code needs them. Those interfaces could be implemented in various ways: You could use a relational database, a document database, files, blobs, etc.
Once I decide to pull the above algorithm into the production code, I'm choosing a particular persistent data structure. This now locks the data storage system into a design where there's a persistent view per date, and another database of bookings.
Now that I'd learned some more about the exercise, I felt confident making that decision.
Template Method #
The first move I made was to create a superclass so that I could employ the Template Method pattern:
public abstract class ReadRegistry : IReadRegistry { public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return EnumerateDates(arrival, departure) .Select(GetView) .Aggregate(Rooms.AsEnumerable(), Enumerable.Intersect) .ToList(); } public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = QueryService.Reserve(booking, view); UpdateView(d, newView); } } protected abstract void UpdateView(DateOnly date, IReadOnlyCollection<Room> view); protected abstract IReadOnlyCollection<Room> Rooms { get; } protected abstract bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view); private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } } private IReadOnlyCollection<Room> GetView(DateOnly date) { if (TryGetView(date, out var view)) return view; else return Rooms; } }
This looks similar to FakeReadRegistry, so how is this an improvement?
The new ReadRegistry class is production code. It can, and should, be tested. (Due to the history of how we got here, it's already covered by tests, so I'm not going to repeat that effort here.)
True to the Template Method pattern, three abstract members await a child class' implementation. These are the UpdateView and TryGetView methods, as well as the Rooms read-only property (glorified getter method).
Imagine that in the production code, these are implemented based on file/document/blob storage - one per date. TryGetView would attempt to read the document from storage, UpdateView would create or modify the document, while Rooms returns a default set of rooms.
A Test Double, however, can still use an in-memory dictionary:
internal sealed class FakeReadRegistry : ReadRegistry { private readonly IReadOnlyCollection<Room> rooms; private readonly IDictionary<DateOnly, IReadOnlyCollection<Room>> views; protected override IReadOnlyCollection<Room> Rooms => rooms; public FakeReadRegistry(params Room[] rooms) { this.rooms = rooms; views = new Dictionary<DateOnly, IReadOnlyCollection<Room>>(); } protected override void UpdateView(DateOnly date, IReadOnlyCollection<Room> view) { views[date] = view; } protected override bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view) { return views.TryGetValue(date, out view); } }
Each override is a one-liner with cyclomatic complexity 1.
First round of clean-up #
An abstract class is already a polymorphic object, so we no longer need the IReadRegistry interface. Delete that, and update all code accordingly. Particularly, the QueryService now depends on ReadRegistry rather than IReadRegistry:
private readonly ReadRegistry readRegistry; public QueryService(ReadRegistry readRegistry) { this.readRegistry = readRegistry; }
Now move the Reserve function from QueryService to ReadRegistry. Once this is done, the QueryService looks like this:
public sealed class QueryService { private readonly ReadRegistry readRegistry; public QueryService(ReadRegistry readRegistry) { this.readRegistry = readRegistry; } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return readRegistry.GetFreeRooms(arrival, departure); } }
That class is only passing method calls along, so clearly no longer serving any purpose. Delete it.
This is a not uncommon in CQRS. One might even argue that if CQRS is done right, there's almost no code on the query side, since all the data view update happens as events propagate.
From abstract class to Dependency Injection #
While the current state of the code is based on an abstract base class, the overall architecture of the system doesn't hinge on inheritance. From Abstract class isomorphism we know that it's possible to refactor an abstract class to Constructor Injection. Let's do that.
First add an IViewStorage interface that mirrors the three abstract methods defined by ReadRegistry:
public interface IViewStorage { IReadOnlyCollection<Room> Rooms { get; } void UpdateView(DateOnly date, IReadOnlyCollection<Room> view); bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view); }
Then implement it with a Fake Object:
public sealed class FakeViewStorage : IViewStorage { private readonly IDictionary<DateOnly, IReadOnlyCollection<Room>> views; public IReadOnlyCollection<Room> Rooms { get; } public FakeViewStorage(params Room[] rooms) { Rooms = rooms; views = new Dictionary<DateOnly, IReadOnlyCollection<Room>>(); } public void UpdateView(DateOnly date, IReadOnlyCollection<Room> view) { views[date] = view; } public bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view) { return views.TryGetValue(date, out view); } }
Notice the similarity to FakeReadRegistry, which we'll get rid of shortly.
Now inject IViewStorage into ReadRegistry, and make ReadRegistry a regular (sealed) class:
public sealed class ReadRegistry { private readonly IViewStorage viewStorage; public ReadRegistry(IViewStorage viewStorage) { this.viewStorage = viewStorage; } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return EnumerateDates(arrival, departure) .Select(GetView) .Aggregate(viewStorage.Rooms.AsEnumerable(), Enumerable.Intersect) .ToList(); } public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = Reserve(booking, view); viewStorage.UpdateView(d, newView); } } public static IReadOnlyCollection<Room> Reserve( Booking booking, IReadOnlyCollection<Room> existingView) { return existingView .Where(r => r.Name != booking.RoomName) .ToList(); } private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } } private IReadOnlyCollection<Room> GetView(DateOnly date) { if (viewStorage.TryGetView(date, out var view)) return view; else return viewStorage.Rooms; } }
You can now delete the FakeReadRegistry Test Double, since FakeViewStorage has now taken its place.
Finally, we may consider if we can make FakeViewStorage even slimmer. While I usually favour composition over inheritance, I've found that deriving Fake Objects from collection base classes is often an efficient way to get a lot of mileage out of a few lines of code. FakeReadRegistry, however, had to inherit from ReadRegistry, so it couldn't derive from any other class.
FakeViewStorage isn't constrained in that way, so it's free to inherit from Dictionary<DateOnly, IReadOnlyCollection<Room>>:
public sealed class FakeViewStorage : Dictionary<DateOnly, IReadOnlyCollection<Room>>, IViewStorage { public IReadOnlyCollection<Room> Rooms { get; } public FakeViewStorage(params Room[] rooms) { Rooms = rooms; } public void UpdateView(DateOnly date, IReadOnlyCollection<Room> view) { this[date] = view; } public bool TryGetView(DateOnly date, out IReadOnlyCollection<Room> view) { return TryGetValue(date, out view); } }
This last move isn't strictly necessary, but I found it worth at least mentioning.
I hope you'll agree that this is a Fake Object that looks maintainable.
Conclusion #
Test-driven development is a feedback mechanism. If something is difficult to test, it tells you something about your System Under Test (SUT). If your test code looks bloated, that tells you something too. Perhaps part of the test code really belongs in the production code.
In this article, we started with a Fake Object that looked like it contained too much production code. Via a series of refactorings I moved the relevant parts to the production code, leaving me with a more idiomatic and conforming implementation.
CC golf
Noun. Game in which the goal is to minimise cyclomatic complexity.
Cyclomatic complexity (CC) is a rare code metric since it can be actually useful. In general, it's a good idea to minimise it as much as possible.
In short, CC measures looping and branching in code, and this is often where bugs lurk. While it's only a rough measure, I nonetheless find the metric useful as a general guideline. Lower is better.
Golf #
I'd like to propose the term "CC golf" for the activity of minimising cyclomatic complexity in an area of code. The name derives from code golf, in which you have to implement some behaviour (typically an algorithm) in fewest possible characters.
Such games can be useful because they enable you to explore different ways to express yourself in code. It's always a good kata constraint. The first time I tried that was in 2011, and when looking back on that code today, I'm not that impressed. Still, it taught me a valuable lesson about the Visitor pattern that I never forgot, and that later enabled me to connect some important dots.
But don't limit CC golf to katas and the like. Try it in your production code too. Most production code I've seen could benefit from some CC golf, and if you use Git tactically you can always stash the changes if they're no good.
Idiomatic tension #
Alternative expressions with lower cyclomatic complexity may not always be idiomatic. Let's look at a few examples. In my previous article, I listed some test code where some helper methods had a CC of 2. Here's one of them:
private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } }
Can you express this functionality with a CC of 1? In Haskell it's essentially built in as (. pred) . enumFromTo, and in F# it's also idiomatic, although more verbose:
let enumerateDates (arrival : DateOnly) departure = Seq.initInfinite id |> Seq.map arrival.AddDays |> Seq.takeWhile (fun d -> d < departure)
Can we do the same in C#?
If there's a general API in .NET that corresponds to the F#-specific Seq.initInfinite I haven't found it, but we can do something like this:
private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { const int infinity = int.MaxValue; // As close as int gets, at least return Enumerable.Range(0, infinity).Select(arrival.AddDays).TakeWhile(d => d < departure); }
In C# infinite sequences are generally unusual, but if you were to create one, a combination of while true and yield return would be the most idiomatic. The problem with that, though, is that such a construct has a cyclomatic complexity of 2.
The above suggestion gets around that problem by pretending that int.MaxValue is infinity. Practically, at least, a 32-bit signed integer can't get larger than that anyway. I haven't tried to let F#'s Seq.initInfinite run out, but by its type it seems int-bound as well, so in practice it, too, probably isn't infinite. (Or, if it is, the index that it supplies will have to overflow and wrap around to a negative value.)
Is this alternative C# code better than the first? You be the judge of that. It has a lower cyclomatic complexity, but is less idiomatic. This isn't uncommon. In languages with a procedural background, there's often tension between lower cyclomatic complexity and how 'things are usually done'.
Checking for null #
Is there a way to reduce the cyclomatic complexity of the GetView helper method?
private IReadOnlyCollection<Room> GetView(DateOnly date) { if (views.TryGetValue(date, out var view)) return view; else return rooms; }
This is an example of the built-in API being in the way. In F#, you naturally write the same behaviour with a CC of 1:
let getView (date : DateOnly) =
views |> Map.tryFind date |> Option.defaultValue rooms |> Set.ofSeq
That TryGet idiom is in the way for further CC reduction, it seems. It is possible to reach a CC of 1, though, but it's neither pretty nor idiomatic:
private IReadOnlyCollection<Room> GetView(DateOnly date) { views.TryGetValue(date, out var view); return new[] { view, rooms }.Where(x => x is { }).First()!; }
Perhaps there's a better way, but if so, it escapes me. Here, I use my knowledge that view is going to remain null if TryGetValue doesn't find the dictionary entry. Thus, I can put it in front of an array where I put the fallback value rooms as the second element. Then I filter the array by only keeping the elements that are not null (that's what the x is { } pun means; I usually read it as x is something). Finally, I return the first of these elements.
I know that rooms is never null, but apparently the compiler can't tell. Thus, I have to suppress its anxiety with the ! operator, telling it that this will result in a non-null value.
I would never use such a code construct in a professional C# code base.
Side effects #
The third helper method suggests another kind of problem that you may run into:
public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = QueryService.Reserve(booking, view); views[d] = newView; } }
Here the higher-than-one CC stems from the need to loop through dates in order to produce a side effect for each. Even in F# I do that:
member this.RoomBooked booking = for d in enumerateDates booking.Arrival booking.Departure do let newView = getView d |> QueryService.reserve booking |> Seq.toList views <- Map.add d newView views
This also has a cyclomatic complexity of 2. You could do something like this:
member this.RoomBooked booking = enumerateDates booking.Arrival booking.Departure |> Seq.iter (fun d -> let newView = getView d |> QueryService.reserve booking |> Seq.toList in views <- Map.add d newView views)
but while that nominally has a CC of 1, it has the same level of indentation as the previous attempt. This seems to indicate, at least, that it doesn't really address any complexity issue.
You could also try something like this:
member this.RoomBooked booking = enumerateDates booking.Arrival booking.Departure |> Seq.map (fun d -> d, getView d |> QueryService.reserve booking |> Seq.toList) |> Seq.iter (fun (d, newView) -> views <- Map.add d newView views)
which, again, may be nominally better, but forced me to wrap the map output in a tuple so that both d and newView is available to Seq.iter. I tend to regard that as a code smell.
This latter version is, however, fairly easily translated to C#:
public void RoomBooked(Booking booking) { EnumerateDates(booking.Arrival, booking.Departure) .Select(d => (d, view: QueryService.Reserve(booking, GetView(d)))) .ToList() .ForEach(x => views[x.d] = x.view); }
The standard .NET API doesn't have something equivalent to Seq.iter (although you could trivially write such an action), but you can convert any sequence to a List<T> and use its ForEach method.
In practice, though, I tend to agree with Eric Lippert. There's already an idiomatic way to iterate over each item in a collection, and being explicit is generally helpful to the reader.
Church encoding #
There's a general solution to most of CC golf: Whenever you need to make a decision and branch between two or more pathways, you can model that with a sum type. In C# you can mechanically model that with Church encoding or the Visitor pattern. If you haven't tried that, I recommend it for the exercise, but once you've done it enough times, you realise that it requires little creativity.
As an example, in 2021 I revisited the Tennis kata with the explicit purpose of translating my usual F# approach to the exercise to C# using Church encoding and the Visitor pattern.
Once you've got a sense for how Church encoding enables you to simulate pattern matching in C#, there are few surprises. You may also rightfully question what is gained from such an exercise:
public IScore VisitPoints(IPoint playerOnePoint, IPoint playerTwoPoint) { return playerWhoWinsBall.Match( playerOne: playerOnePoint.Match<IScore>( love: new Points(new Fifteen(), playerTwoPoint), fifteen: new Points(new Thirty(), playerTwoPoint), thirty: new Forty(playerWhoWinsBall, playerTwoPoint)), playerTwo: playerTwoPoint.Match<IScore>( love: new Points(playerOnePoint, new Fifteen()), fifteen: new Points(playerOnePoint, new Thirty()), thirty: new Forty(playerWhoWinsBall, playerOnePoint))); }
Believe it or not, but that method has a CC of 1 despite the double indentation strongly suggesting that there's some branching going on. To a degree, this also highlights the limitations of the cyclomatic complexity metric. Conversely, stupidly simple code may have a high CC rating.
Most of the examples in this article border on the pathological, and I don't recommend that you write code like that. I recommend that you do the exercise. In less pathological scenarios, there are real benefits to be reaped.
Idioms #
In 2015 I published an article titled Idiomatic or idiosyncratic? In it, I tried to explore the idea that the notion of idiomatic code can sometimes hold you back. I revisited that idea in 2021 in an article called Against consistency. The point in both cases is that just because something looks unfamiliar, it doesn't mean that it's bad.
Coding idioms somehow arose. If you believe that there's a portion of natural selection involved in the development of coding idioms, you may assume by default that idioms represent good ways of doing things.
To a degree I believe this to be true. Many idioms represent the best way of doing things at the time they settled into the shape that we now know them. Languages and contexts change, however. Just look at the many approaches to data lookups there have been over the years. For many years now, C# has settled into the so-called TryParse idiom to solve that problem. In my opinion this represents a local maximum.
Languages that provide Maybe (AKA option) and Either (AKA Result) types offer a superior alternative. These types naturally compose into CC 1 pipelines, whereas TryParse requires you to stop what you're doing in order to check a return value. How very C-like.
All that said, I still think you should write idiomatic code by default, but don't be a slave by what's considered idiomatic, just as you shouldn't be a slave to consistency. If there's a better way of doing things, choose the better way.
Conclusion #
While cyclomatic complexity is a rough measure, it's one of the few useful programming metrics I know of. It should be as low as possible.
Most professional code I encounter implements decisions almost exclusively with language primitives: if, for, switch, while, etc. Once, an organisation hired me to give a one-day anti-if workshop. There are other ways to make decisions in code. Most of those alternatives reduce cyclomatic complexity.
That's not really a goal by itself, but reducing cyclomatic complexity tends to produce the beneficial side effect of structuring the code in a more sustainable way. It becomes easier to understand and change.
As the cliché goes: Choose the right tool for the job. You can't, however, do that if you have nothing to choose from. If you only know of one way to do a thing, you have no choice.
Play a little CC golf with your code from time to time. It may improve the code, or it may not. If it didn't, just stash those changes. Either way, you've probably learned something.
Fakes are Test Doubles with contracts
Contracts of Fake Objects can be described by properties.
The first time I tried my hand with the CQRS Booking kata, I abandoned it after 45 minutes because I found that I had little to learn from it. After all, I've already done umpteen variations of (restaurant) booking code examples, in several programming languages. The code example that accompanies my book Code That Fits in Your Head is only the largest and most complete of those.
I also wrote an MSDN Magazine article in 2011 about CQRS, so I think I have that angle covered as well.
Still, while at first glance the kata seemed to have little to offer me, I've found myself coming back to it a few times. It does enable me to focus on something else than the 'production code'. In fact, it turns out that even if (or perhaps particularly when) you use test-driven development (TDD), there's precious little production code. Let's get that out of the way first.
Production code #
The few times I've now done the kata, there's almost no 'production code'. The implied CommandService has two lines of effective code:
public sealed class CommandService { private readonly IWriteRegistry writeRegistry; private readonly IReadRegistry readRegistry; public CommandService(IWriteRegistry writeRegistry, IReadRegistry readRegistry) { this.writeRegistry = writeRegistry; this.readRegistry = readRegistry; } public void BookARoom(Booking booking) { writeRegistry.Save(booking); readRegistry.RoomBooked(booking); } }
The QueryService class isn't much more exciting:
public sealed class QueryService { private readonly IReadRegistry readRegistry; public QueryService(IReadRegistry readRegistry) { this.readRegistry = readRegistry; } public static IReadOnlyCollection<Room> Reserve( Booking booking, IReadOnlyCollection<Room> existingView) { return existingView.Where(r => r.Name != booking.RoomName).ToList(); } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return readRegistry.GetFreeRooms(arrival, departure); } }
The kata only suggests the GetFreeRooms method, which is only a single line. The only reason the Reserve function also exists is to pull a bit of testable logic back from the below Fake object. I'll return to that shortly.
I've also done the exercise in F#, essentially porting the C# implementation, which only highlights how simple it all is:
module CommandService = let bookARoom (writeRegistry : IWriteRegistry) (readRegistry : IReadRegistry) booking = writeRegistry.Save booking readRegistry.RoomBooked booking module QueryService = let reserve booking existingView = existingView |> Seq.filter (fun r -> r.Name <> booking.RoomName) let getFreeRooms (readRegistry : IReadRegistry) arrival departure = readRegistry.GetFreeRooms arrival departure
That's both the Command side and the Query side!
This represents my honest interpretation of the kata. Really, there's nothing to it.
The reason I still find the exercise interesting is that it explores other aspects of TDD than most katas. The most common katas require you to write a little algorithm: Bowling, Word wrap, Roman Numerals, Diamond, Tennis, etc.
The CQRS Booking kata suggests no interesting algorithm, but rather teaches some important lessons about software architecture, separation of concerns, and, if you approach it with TDD, real-world test automation. In contrast to all those algorithmic exercises, this one strongly suggests the use of Test Doubles.
Fakes #
You could attempt the kata with a dynamic 'mocking' library such as Moq or Mockito, but I haven't tried. Since Stubs and Mocks break encapsulation I favour Fake Objects instead.
Creating a Fake write registry is trivial:
internal sealed class FakeWriteRegistry : Collection<Booking>, IWriteRegistry { public void Save(Booking booking) { Add(booking); } }
Its counterpart, the Fake read registry, turns out to be much more involved:
internal sealed class FakeReadRegistry : IReadRegistry { private readonly IReadOnlyCollection<Room> rooms; private readonly IDictionary<DateOnly, IReadOnlyCollection<Room>> views; public FakeReadRegistry(params Room[] rooms) { this.rooms = rooms; views = new Dictionary<DateOnly, IReadOnlyCollection<Room>>(); } public IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure) { return EnumerateDates(arrival, departure) .Select(GetView) .Aggregate(rooms.AsEnumerable(), Enumerable.Intersect) .ToList(); } public void RoomBooked(Booking booking) { foreach (var d in EnumerateDates(booking.Arrival, booking.Departure)) { var view = GetView(d); var newView = QueryService.Reserve(booking, view); views[d] = newView; } } private static IEnumerable<DateOnly> EnumerateDates(DateOnly arrival, DateOnly departure) { var d = arrival; while (d < departure) { yield return d; d = d.AddDays(1); } } private IReadOnlyCollection<Room> GetView(DateOnly date) { if (views.TryGetValue(date, out var view)) return view; else return rooms; } }
I think I can predict the most common reaction: That's much more code than the System Under Test! Indeed. For this particular exercise, this may indicate that a 'dynamic mock' library may have been a better choice. I do, however, also think that it's an artefact of the kata description's lack of requirements.
As is evident from the restaurant sample code that accompanies Code That Fits in Your Head, once you add realistic business rules the production code grows, and the ratio of test code to production code becomes better balanced.
The size of the FakeReadRegistry class also stems from the way the .NET base class library API is designed. The GetView helper method demonstrates that it requires four lines of code to look up an entry in a dictionary but return a default value if the entry isn't found. That's a one-liner in F#:
let getView (date : DateOnly) = views |> Map.tryFind date |> Option.defaultValue rooms |> Set.ofSeq
I'll show the entire F# Fake later, but you could also play some CC golf with the C# code. That's a bit besides the point, though.
Command service design #
Why does FakeReadRegistry look like it does? It's a combination of the kata description and my prior experience with CQRS. When adopting an asynchronous message-based architecture, I would usually not implement the write side exactly like that. Notice how the CommandService class' BookARoom method seems to repeat itself:
public void BookARoom(Booking booking) { writeRegistry.Save(booking); readRegistry.RoomBooked(booking); }
While semantically it seems to be making two different statements, structurally they're identical. If you rename the methods, you could wrap both method calls in a single Composite. In a more typical CQRS architecture, you'd post a Command on bus:
public void BookARoom(Booking booking) { bus.BookRoom(booking); }
This makes that particular BookARoom method, and perhaps the entire CommandService class, look redundant. Why do we need it?
As presented here, we don't, but in a real application, the Command service would likely perform some pre- and post-processing. For example, if this was a web application, the Command service might instead be a Controller concerned with validating and translating HTTP- or Web-based input to a Domain Object before posting to the bus.
A realistic code base would also be asynchronous, which, on .NET, would imply the use of the async and await keywords, etc.
Read registry design #
A central point of CQRS is that you can optimise the read side for the specific tasks that it needs to perform. Instead of performing a dynamic query every time a client requests a view, you can update and persist a view. Imagine having a JSON or HTML file that the system can serve upon request.
Part of handling a Command or Event is that the system background processes update persistent views once per event.
For the particular hotel booking system, I imagine that the read registry has a set of files, blobs, documents, or denormalised database rows. When it receives notification of a booking, it'll need to remove that room from the dates of the booking.
While a booking may stretch over several days, I found it simplest to think of the storage system as subdivided into single dates, instead of ranges. Indeed, the GetFreeRooms method is a ranged query, so if you really wanted to denormalise the views, you could create a persistent view per range. This would, however, require that you precalculate and persist a view for October 2 to October 4, and another one for October 2 to October 5, and so on. The combinatorial explosion suggests that this isn't a good idea, so instead I imagine keeping a persistent view per date, and then perform a bit of on-the-fly calculation per query.
That's what FakeReadRegistry does. It also falls back to a default collection of rooms for all the dates that are yet untouched by a booking. This is, again, because I imagine that I might implement a real system like that.
You may still protest that the FakeReadRegistry duplicates production code. True, perhaps, but if this really is a concern, you could refactor it to the Template Method pattern.
Still, it's not really that complicated; it only looks that way because C# and the Dictionary API is too heavy on ceremony. The Fake looks much simpler in F#:
type FakeReadRegistry (rooms : IReadOnlyCollection<Room>) = let mutable views = Map.empty let enumerateDates (arrival : DateOnly) departure = Seq.initInfinite id |> Seq.map arrival.AddDays |> Seq.takeWhile (fun d -> d < departure) let getView (date : DateOnly) = views |> Map.tryFind date |> Option.defaultValue rooms |> Set.ofSeq interface IReadRegistry with member this.GetFreeRooms arrival departure = enumerateDates arrival departure |> Seq.map getView |> Seq.fold Set.intersect (Set.ofSeq rooms) |> Set.toList :> _ member this.RoomBooked booking = for d in enumerateDates booking.Arrival booking.Departure do let newView = getView d |> QueryService.reserve booking |> Seq.toList views <- Map.add d newView views
This isn't just more dense than the corresponding C# code, as F# tends to be, it also has a lower cyclomatic complexity. Both the EnumerateDates and GetView C# methods have a cyclomatic complexity of 2, while their F# counterparts rate only 1.
For production code, cyclomatic complexity of 2 is fine if the code is covered by automatic tests. In test code, however, we should be wary of any branching or looping, since there are (typically) no tests of the test code.
While I am going to show some tests of that code in what follows, I do that for a different reason.
Contract #
When explaining Fake Objects to people, I've begun to use a particular phrase:
A Fake Object is a polymorphic implementation of a dependency that fulfils the contract, but lacks some of the ilities.
It's funny how you can arrive at something that strikes you as profound, only to discover that it was part of the definition all along:
"We acquire or build a very lightweight implementation of the same functionality as provided by a component on which the SUT [System Under Test] depends and instruct the SUT to use it instead of the real DOC [Depended-On Component]. This implementation need not have any of the "-ilities" that the real DOC needs to have"
A common example is a Fake Repository object that pretends to be a database, often by leveraging a built-in collection API. The above FakeWriteRegistry is as simple an example as you could have. A slightly more compelling example is the FakeUserRepository shown in another article. Such an 'in-memory database' fulfils the implied contract, because if you 'save' something in the 'database' you can later retrieve it again with a query. As long as the object remains in memory.
The ilities that such a Fake database lacks are
- data persistence
- thread safety
- transaction support
and perhaps others. Such qualities are clearly required in a real production environment, but are in the way in an automated testing context. The implied contract, however, is satisfied: What you save you can later retrieve.
Now consider the IReadRegistry interface:
public interface IReadRegistry { IReadOnlyCollection<Room> GetFreeRooms(DateOnly arrival, DateOnly departure); void RoomBooked(Booking booking); }
Which contract does it imply, given what you know about the CQRS Booking kata?
I would suggest the following:
- Precondition:
arrivalshould be less than (or equal?) todeparture. - Postcondition:
GetFreeRoomsshould always return a result. Null isn't a valid return value. - Invariant: After calling
RoomBooked,GetFreeRoomsshould exclude that room when queried on overlapping dates.
There may be other parts of the contract than this, but I find the third one most interesting. This is exactly what you would expect from a real system: If you reserve a room, you'd be surprised to see GetFreeRooms indicating that this room is free if queried about dates that overlap the reservation.
This is the sort of implied interaction that Stubs and Mocks break, but that FakeReadRegistry guarantees.
Properties #
There's a close relationship between contracts and properties. Once you can list preconditions, invariants, and postconditions for an object, there's a good chance that you can write code that exercises those qualities. Indeed, why not use property-based testing to do so?
I don't wish to imply that you should (normally) write tests of your test code. The following rather serves as a concretisation of the notion that a Fake Object is a Test Double that implements the 'proper' behaviour. In the following, I'll subject the FakeReadRegistry class to that exercise. To do that, I'll use CsCheck 2.14.1 with xUnit.net 2.5.3.
Before tackling the above invariant, there's a simpler invariant specific to the FakeReadRegistry class. A FakeReadRegistry object takes a collection of rooms via its constructor, so for this particular implementation, we may wish to establish the reasonable invariant that GetFreeRooms doesn't 'invent' rooms on its own:
private static Gen<Room> GenRoom => from name in Gen.String select new Room(name); [Fact] public void GetFreeRooms() { (from rooms in GenRoom.ArrayUnique from arrival in Gen.Date.Select(DateOnly.FromDateTime) from i in Gen.Int[1, 1_000] let departure = arrival.AddDays(i) select (rooms, arrival, departure)) .Sample((rooms, arrival, departure) => { var sut = new FakeReadRegistry(rooms); var actual = sut.GetFreeRooms(arrival, departure); Assert.Subset(new HashSet<Room>(rooms), new HashSet<Room>(actual)); }); }
This property asserts that the actual value returned from GetFreeRooms is a subset of the rooms used to initialise the sut. Recall that the subset relation is reflexive; i.e. a set is a subset of itself.
The same property written in F# with Hedgehog 0.13.0 and Unquote 6.1.0 may look like this:
module Gen = let room = Gen.alphaNum |> Gen.array (Range.linear 1 10) |> Gen.map (fun chars -> { Name = String chars }) let dateOnly = let min = DateOnly(2000, 1, 1).DayNumber let max = DateOnly(2100, 1, 1).DayNumber Range.linear min max |> Gen.int32 |> Gen.map DateOnly.FromDayNumber [<Fact>] let GetFreeRooms () = Property.check <| property { let! rooms = Gen.room |> Gen.list (Range.linear 0 100) let! arrival = Gen.dateOnly let! i = Gen.int32 (Range.linear 1 1_000) let departure = arrival.AddDays i let sut = FakeReadRegistry rooms :> IReadRegistry let actual = sut.GetFreeRooms arrival departure test <@ Set.isSubset (Set.ofSeq rooms) (Set.ofSeq actual) @> }
Simpler syntax, same idea.
Likewise, we can express the contract that describes the relationship between RoomBooked and GetFreeRooms like this:
[Fact] public void RoomBooked() { (from rooms in GenRoom.ArrayUnique.Nonempty from arrival in Gen.Date.Select(DateOnly.FromDateTime) from i in Gen.Int[1, 1_000] let departure = arrival.AddDays(i) from room in Gen.OneOfConst(rooms) from id in Gen.Guid let booking = new Booking(id, room.Name, arrival, departure) select (rooms, booking)) .Sample((rooms, booking) => { var sut = new FakeReadRegistry(rooms); sut.RoomBooked(booking); var actual = sut.GetFreeRooms(booking.Arrival, booking.Departure); Assert.DoesNotContain(booking.RoomName, actual.Select(r => r.Name)); }); }
or, in F#:
[<Fact>] let RoomBooked () = Property.check <| property { let! rooms = Gen.room |> Gen.list (Range.linear 1 100) let! arrival = Gen.dateOnly let! i = Gen.int32 (Range.linear 1 1_000) let departure = arrival.AddDays i let! room = Gen.item rooms let! id = Gen.guid let booking = { ClientId = id RoomName = room.Name Arrival = arrival Departure = departure } let sut = FakeReadRegistry rooms :> IReadRegistry sut.RoomBooked booking let actual = sut.GetFreeRooms arrival departure test <@ not (Seq.contains room actual) @> }
In both cases, the property books a room and then proceeds to query GetFreeRooms to see which rooms are free. Since the query is exactly in the range from booking.Arrival to booking.Departure, we expect not to see the name of the booked room among the free rooms.
(As I'm writing this, I think that there may be a subtle bug in the F# property. Can you spot it?)
Conclusion #
A Fake Object isn't like other Test Doubles. While Stubs and Mocks break encapsulation, a Fake Object not only stays encapsulated, but it also fulfils the contract implied by a polymorphic API (interface or base class).
Or, put another way: When is a Fake Object the right Test Double? When you can describe the contract of the dependency.
But if you can't describe the contract of a dependency, you should seriously consider if the design is right.
A C# port of validation with partial round trip
A raw port of the previous F# demo code.
This article is part of a short article series on applicative validation with a twist. The twist is that validation, when it fails, should return not only a list of error messages; it should also retain that part of the input that was valid.
In the previous article I showed F# demo code, and since the original forum question that prompted the article series was about F# code, for a long time, I left it there.
Recently, however, I've found myself writing about validation in a broader context:
- An applicative reservation validation example in C#
- ASP.NET validation revisited
- Can types replace validation?
- Validation and business rules
- Validating or verifying emails
Perhaps I should consider adding a validation tag to the blog...
In that light I thought that it might be illustrative to continue this article series with a port to C#.
Here, I use techniques already described on this site to perform the translation. Follow the links for details.
The translation given here is direct so produces some fairly non-idiomatic C# code.
Building blocks #
The original problem is succinctly stated, and I follow it as closely as possible. This includes potential errors that may be present in the original post.
The task is to translate some input to a Domain Model with good encapsulation. The input type looks like this, translated to a C# record:
public sealed record Input(string? Name, DateTime? DoB, string? Address)
Notice that every input may be null. This indicates poor encapsulation, but is symptomatic of most input. At the boundaries, static types are illusory. Perhaps it would have been more idiomatic to model such input as a Data Transfer Object, but it makes little difference to what comes next.
I consider validation a solved problem, because it's possible to model the process as an applicative functor. Really, validation is a parsing problem.
Since my main intent with this article is to demonstrate a technique, I will allow myself a few shortcuts. Like I did when I first encountered the Args kata, I start by copying the Validated code from An applicative reservation validation example in C#; you can go there if you're interested in it. I'm not going to repeat it here.
The target type looks similar to the above Input record, but doesn't allow null values:
public sealed record ValidInput(string Name, DateTime DoB, string Address);
This could also have been a 'proper' class. The following code doesn't depend on that.
Validating names #
Since I'm now working in an ostensibly object-oriented language, I can make the various validation functions methods on the Input record. Since I'm treating validation as a parsing problem, I'm going to name those methods with the TryParse prefix:
private Validated<(Func<Input, Input>, IReadOnlyCollection<string>), string> TryParseName() { if (Name is null) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), string>( (x => x, new[] { "name is required" })); if (Name.Length <= 3) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), string>( (i => i with { Name = null }, new[] { "no bob and toms allowed" })); return Validated.Succeed<(Func<Input, Input>, IReadOnlyCollection<string>), string>(Name); }
As the two previous articles have explained, the result of trying to parse input is a type isomorphic to Either, but here called Validated<F, S>. (The reason for this distinction is that we don't want the monadic behaviour of Either, because monads short-circuit.)
When parsing succeeds, the TryParseName method returns the Name wrapped in a Success case.
Parsing the name may fail in two different ways. If the name is missing, the method returns the input and the error message "name is required". If the name is present, but too short, TryParseName returns another error message, and also resets Name to null.
Compare the C# code with the corresponding F# or Haskell code and notice how much more verbose the C# has to be.
While it's possible to translate many functional programming concepts to a language like C#, syntax does matter, because it affects readability.
Validating date of birth #
From here, the port is direct, if awkward. Here's how to validate the date-of-birth field:
private Validated<(Func<Input, Input>, IReadOnlyCollection<string>), DateTime> TryParseDoB(DateTime now) { if (!DoB.HasValue) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), DateTime>( (x => x, new[] { "dob is required" })); if (DoB.Value <= now.AddYears(-12)) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), DateTime>( (i => i with { DoB = null }, new[] { "get off my lawn" })); return Validated.Succeed<(Func<Input, Input>, IReadOnlyCollection<string>), DateTime>( DoB.Value); }
I suspect that the age check should really have been a greater-than relation, but I'm only reproducing the original code.
Validating addresses #
The final building block is to parse the input address:
private Validated<(Func<Input, Input>, IReadOnlyCollection<string>), string> TryParseAddress() { if (Address is null) return Validated.Fail<(Func<Input, Input>, IReadOnlyCollection<string>), string>( (x => x, new[] { "add1 is required" })); return Validated.Succeed<(Func<Input, Input>, IReadOnlyCollection<string>), string>( Address); }
The TryParseAddress only checks whether or not the Address field is present.
Composition #
The above methods are private because the entire problem is simple enough that I can test the composition as a whole. Had I wanted to, however, I could easily have made them public and tested them individually.
You can now use applicative composition to produce a single validation method:
public Validated<(Input, IReadOnlyCollection<string>), ValidInput> TryParse(DateTime now) { var name = TryParseName(); var dob = TryParseDoB(now); var address = TryParseAddress(); Func<string, DateTime, string, ValidInput> createValid = (n, d, a) => new ValidInput(n, d, a); static (Func<Input, Input>, IReadOnlyCollection<string>) combineErrors( (Func<Input, Input> f, IReadOnlyCollection<string> es) x, (Func<Input, Input> g, IReadOnlyCollection<string> es) y) { return (z => y.g(x.f(z)), y.es.Concat(x.es).ToArray()); } return createValid .Apply(name, combineErrors) .Apply(dob, combineErrors) .Apply(address, combineErrors) .SelectFailure(x => (x.Item1(this), x.Item2)); }
This is where the Validated API is still awkward. You need to explicitly define a function to compose error cases. In this case, combineErrors composes the endomorphisms and concatenates the collections.
The final step 'runs' the endomorphism. x.Item1 is the endomorphism, and this is the Input value being validated. Again, this isn't readable in C#, but it's where the endomorphism removes the invalid values from the input.
Tests #
Since applicative validation is a functional technique, it's intrinsically testable.
Testing a successful validation is as easy as this:
[Fact] public void ValidationSucceeds() { var now = DateTime.Now; var eightYearsAgo = now.AddYears(-8); var input = new Input("Alice", eightYearsAgo, "x"); var actual = input.TryParse(now); var expected = Validated.Succeed<(Input, IReadOnlyCollection<string>), ValidInput>( new ValidInput("Alice", eightYearsAgo, "x")); Assert.Equal(expected, actual); }
As is often the case, the error conditions are more numerous, or more interesting, if you will, than the success case, so this requires a parametrised test:
[Theory, ClassData(typeof(ValidationFailureTestCases))] public void ValidationFails( Input input, Input expected, IReadOnlyCollection<string> expectedMessages) { var now = DateTime.Now; var actual = input.TryParse(now); var (inp, msgs) = Assert.Single(actual.Match( onFailure: x => new[] { x }, onSuccess: _ => Array.Empty<(Input, IReadOnlyCollection<string>)>())); Assert.Equal(expected, inp); Assert.Equal(expectedMessages, msgs); }
I also had to take actual apart in order to inspects its individual elements. When working with a pure and immutable data structure, I consider that a test smell. Rather, one should be able to use structural equality for better tests. Unfortunately, .NET collections don't have structural equality, so the test has to pull the message collection out of actual in order to verify it.
Again, in F# or Haskell you don't have that problem, and the tests are much more succinct and robust.
The test cases are implemented by this nested ValidationFailureTestCases class:
private class ValidationFailureTestCases : TheoryData<Input, Input, IReadOnlyCollection<string>> { public ValidationFailureTestCases() { Add(new Input(null, null, null), new Input(null, null, null), new[] { "add1 is required", "dob is required", "name is required" }); Add(new Input("Bob", null, null), new Input(null, null, null), new[] { "add1 is required", "dob is required", "no bob and toms allowed" }); Add(new Input("Alice", null, null), new Input("Alice", null, null), new[] { "add1 is required", "dob is required" }); var eightYearsAgo = DateTime.Now.AddYears(-8); Add(new Input("Alice", eightYearsAgo, null), new Input("Alice", eightYearsAgo, null), new[] { "add1 is required" }); var fortyYearsAgo = DateTime.Now.AddYears(-40); Add(new Input("Alice", fortyYearsAgo, "x"), new Input("Alice", null, "x"), new[] { "get off my lawn" }); Add(new Input("Tom", fortyYearsAgo, "x"), new Input(null, null, "x"), new[] { "get off my lawn", "no bob and toms allowed" }); Add(new Input("Tom", eightYearsAgo, "x"), new Input(null, eightYearsAgo, "x"), new[] { "no bob and toms allowed" }); } }
All eight tests pass.
Conclusion #
Once you know how to model sum types (discriminated unions) in C#, translating something like applicative validation isn't difficult per se. It's a fairly automatic process.
The code is hardly idiomatic C#, and the type annotations are particularly annoying. Things work as expected though, and it isn't difficult to imagine how one could refactor some of this code to a more idiomatic form.
Domain Model first
Persistence concerns second.
A few weeks ago, I published an article with the title Do ORMs reduce the need for mapping? Not surprisingly, this elicited more than one reaction. In this article, I'll respond to a particular kind of reaction.
First, however, I'd like to reiterate the message of the previous article, which is almost revealed by the title: Do object-relational mappers (ORMs) reduce the need for mapping? To which the article answers a tentative no.
Do pay attention to the question. It doesn't ask whether ORMs are bad in general, or in all cases. It mainly analyses whether the use of ORMs reduces the need to write code that maps between different representations of data: From database to objects, from objects to Data Transfer Objects (DTOs), etc.
Granted, the article looks at a wider context, which I think is only a responsible thing to do. This could lead some readers to extrapolate from the article's specific focus to draw a wider conclusion.
Encapsulation-first #
Most of the systems I work with aren't CRUD systems, but rather systems where correctness is important. As an example, one of my clients does security-heavy digital infrastructure. Earlier in my career, I helped write web shops when these kinds of systems were new. Let me tell you: System owners were quite concerned that prices were correct, and that orders were taken and handled without error.
In my book Code That Fits in Your Head I've tried to capture the essence of those kinds of system with the accompanying sample code, which pretends to be an online restaurant reservation system. While this may sound like a trivial CRUD system, the business logic isn't entirely straightforward.
The point I was making in the previous article is that I consider encapsulation to be more important than 'easy' persistence. I don't mind writing a bit of mapping code, since typing isn't a programming bottleneck anyway.
When prioritising encapsulation you should be able to make use of any design pattern, run-time assertion, as well as static type systems (if you're working in such a language) to guard correctness. You should be able to compose objects, define Value Objects, wrap single values to avoid primitive obsession, make constructors private, leverage polymorphism and effectively use any trick your language, idiom, and platform has on offer. If you want to use Church encoding or the Visitor pattern to represent a sum type, you should be able to do that.
When writing these kinds of systems, I start with the Domain Model without any thought of how to persist or retrieve data.
In my experience, once the Domain Model starts to congeal, the persistence question tends to answer itself. There's usually one or two obvious ways to store and read data.
Usually, a relational database isn't the most obvious choice.
Persistence ignorance #
Write the best API you can to solve the problem, and then figure out how to store data. This is the allegedly elusive ideal of persistence ignorance, which turns out to be easier than rumour has it, once you cast a wider net than relational databases.
It seems to me, though, that more than one person who has commented on my previous article have a hard time considering alternatives. And granted, I've consulted with clients who knew how to operate a particular database system, but nothing else, and who didn't want to consider adopting another technology. I do understand that such constraints are real, too. Thus, if you need to compromise for reasons such as these, you aren't doing anything wrong. You may still, however, try to get the best out of the situation.
One client of mine, for example, didn't want to operate anything else than SQL Server, which they already know. For an asynchronous message-based system, then, we chose NServiceBus and configured it to use SQL Server as a persistent queue.
Several comments still seem to assume that persistence must look in a particular way.
"So having a Order, OrderLine, Person, Address and City, all the rows needed to be loaded in advance, mapped to objects and references set to create the object graph to be able to, say, display shipping costs based on person's address."
I don't wish to single out Vlad, but this is both the first comment, and it captures the essence of other comments well. I imagine that what he has in mind is something like this:
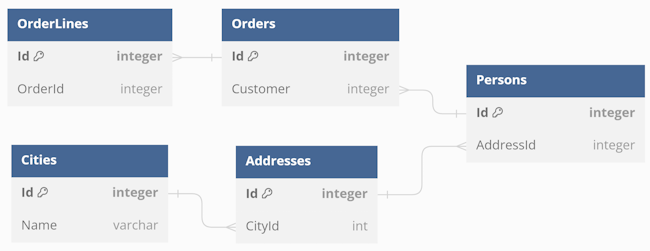
I've probably simplified things a bit too much. In a more realistic model, each person may have a collection of addresses, instead of just one. If so, it only strengthens Vlad's point, because that would imply even more tables to read.
The unstated assumption, however, is that a fully normalised relational data model is the correct way to store such data.
It's not. As I already mentioned, I spent the first four years of my programming career developing web shops. Orders were an integral part of that work.
An order is a document. You don't want the customer's address to be updatable after the fact. With a normalised relational model, if you change the customer's address row in the future, it's going to look as though the order went to that address instead of the address it actually went to.
This also explains why the order lines should not point to the actually product entries in the product catalogue. Trust me, I almost shipped such a system once, when I was young and inexperienced.
You should, at the very least, denormalise the database model. To a degree, this has already happened here, since the implied order has order lines, that, I hope, are copies of the relevant product data, rather than linked to the product catalogue.
Such insights, however, suggest that other storage mechanisms may be more appropriate.
Putting that aside for a moment, though, how would a persistence-ignorant Domain Model look?
I'd probably start with something like this:
var order = new Order( new Person("Olive", "Hoyle", new Address("Green Street 15", new City("Oakville"), "90125")), new OrderLine(123, 1), new OrderLine(456, 3), new OrderLine(789, 2));
(As the ZIP code implies, I'm more of a Yes fan, but still can't help but relish writing new Order in code.)
With code like this, many a DDD'er would start talking about Aggregate Roots, but that is, frankly, a concept that never made much sense to me. Rather, the above order is a tree composed of immutable data structures.
It trivially serializes to e.g. JSON:
{
"customer": {
"firstName": "Olive",
"lastName": "Hoyle",
"address": {
"street": "Green Street 15",
"city": { "name": "Oakville" },
"zipCode": "90125"
}
},
"orderLines": [
{
"sku": 123,
"quantity": 1
},
{
"sku": 456,
"quantity": 3
},
{
"sku": 789,
"quantity": 2
}
]
}
All of this strongly suggests that this kind of data would be much easier to store and retrieve with a document database instead of a relational database.
While that's just one example, it strikes me as a common theme when discussing persistence. For most online transaction processing systems, relational database aren't necessarily the best fit.
The cart before the horse #
Another comment also starts with the premise that a data model is fundamentally relational. This one purports to model the relationship between sheikhs, their wives, and supercars. While I understand that the example is supposed to be tongue-in-cheek, the comment launches straight into problems with how to read and persist such data without relying on an ORM.
Again, I don't intend to point fingers at anyone, but on the other hand, I can't suggest alternatives when a problem is presented like that.
The whole point of developing a Domain Model first is to find a good way to represent the business problem in a way that encourages correctness and ease of use.
If you present me with a relational model without describing the business goals you're trying to achieve, I don't have much to work with.
It may be that your business problem is truly relational, in which case an ORM probably is a good solution. I wrote as much in the previous article.
In many cases, however, it looks to me as though programmers start with a relational model, only to proceed to complain that it's difficult to work with in object-oriented (or functional) code.
If you, on the other hand, start with the business problem and figure out how to model it in code, the best way to store the data may suggest itself. Document databases are often a good fit, as are event stores. I've never had need for a graph database, but perhaps that would be a better fit for the sheikh domain suggested by qfilip.
Reporting #
While I no longer feel that relational databases are particularly well-suited for online transaction processing, they are really good at one thing: Ad-hoc querying. Because it's such a rich and mature type of technology, and because SQL is a powerful language, you can slice and dice data in multiple ways.
This makes relational databases useful for reporting and other kinds of data extraction tasks.
You may have business stakeholders who insist on a relational database for that particular reason. It may even be a good reason.
If, however, the sole purpose of having a relational database is to support reporting, you may consider setting it up as a secondary system. Keep your online transactional data in another system, but regularly synchronize it to a relational database. If the only purpose of the relational database is to support reporting, you can treat it as a read-only system. This makes synchronization manageable. In general, you should avoid two-way synchronization if at all possible, but one-way synchronization is usually less of a problem.
Isn't that going to be more work, or more expensive?
That question, again, has no single answer. Of course setting up and maintaining two systems is more work at the outset. On the other hand, there's a perpetual cost to be paid if you come up with the wrong architecture. If development is slow, and you have many bugs in production, or similar problems, the cause could be that you've chosen the wrong architecture and you're now fighting a losing battle.
On the other hand, if you relegate relational databases exclusively to a reporting role, chances are that there's a lot of off-the-shelf software that can support your business users. Perhaps you can even hire a paratechnical power user to take care of that part of the system, freeing you to focus on the 'actual' system.
All of this is only meant as inspiration. If you don't want to, or can't, do it that way, then this article doesn't help you.
Conclusion #
When discussing databases, and particularly ORMs, some people approach the topic with the unspoken assumption that a relational database is the only option for storing data. Many programmers are so skilled in relational data design that they naturally use those skills when thinking new problems over.
Sometimes problems are just relational in nature, and that's fine. More often than not, however, that's not the case.
Try to model a business problem without concern for storage and see where that leads you. Test-driven development is often a great technique for such a task. Then, once you have a good API, consider how to store the data. The Domain Model that you develop in that way may naturally suggest a good way to store and retrieve the data.
At the boundaries, static types are illusory
Static types are useful, but have limitations.
Regular readers of this blog may have noticed that I like static type systems. Not the kind of static types offered by C, which strikes me as mostly being able to distinguish between way too many types of integers and pointers. A good type system is more than just numbers on steroids. A type system like C#'s is workable, but verbose. The kind of type system I find most useful is when it has algebraic data types and good type inference. The examples that I know best are the type systems of F# and Haskell.
As great as static type systems can be, they have limitations. Hillel Wayne has already outlined one kind of distinction, but here I'd like to focus on another constraint.
Application boundaries #
Any piece of software interacts with the 'rest of the world'; effectively everything outside its own process. Sometimes (but increasingly rarely) such interaction is exclusively by way of some user interface, but more and more, an application interacts with other software in some way.

Here I've drawn the application as an opaque disc in order to emphasise that what happens inside the process isn't pertinent to the following discussion. The diagram also includes some common kinds of traffic. Many applications rely on some kind of database or send messages (email, SMS, Commands, Events, etc.). We can think of such traffic as the interactions that the application initiates, but many systems also receive and react to incoming data: HTTP traffic or messages that arrive on a queue, and so on.
When I talk about application boundaries, I have in mind what goes on in that interface layer.
An application can talk to the outside world in multiple ways: It may read or write a file, access shared memory, call operating-system APIs, send or receive network packets, etc. Usually you get to program against higher-level abstractions, but ultimately the application is dealing with various binary protocols.
Protocols #
The bottom line is that at a sufficiently low level of abstraction, what goes in and out of your application has no static type stronger than an array of bytes.
You may counter-argue that higher-level APIs deal with that to present the input and output as static types. When you interact with a text file, you'll typically deal with a list of strings: One for each line in the file. Or you may manipulate JSON, XML, Protocol Buffers, or another wire format using a serializer/deserializer API. Sometime, as is often the case with CSV, you may need to write a very simple parser yourself. Or perhaps something slightly more involved.
To demonstrate what I mean, there's no shortage of APIs like JsonSerializer.Deserialize, which enables you to write code like this:
let n = JsonSerializer.Deserialize<Name> (json, opts)
and you may say: n is statically typed, and its type is Name! Hooray! But you do realise that that's only half a truth, don't you?
An interaction at the application boundary is expected to follow some kind of protocol. This is even true if you're reading a text file. In these modern times, you may expect a text file to contain Unicode, but have you ever received a file from a legacy system and have to deal with its EBCDIC encoding? Or an ASCII file with a code page different from the one you expect? Or even just a file written on a Unix system, if you're on Windows, or vice versa?
In order to correctly interpret or transmit such data, you need to follow a protocol.
Such a protocol can be low-level, as the character-encoding examples I just listed, but it may also be much more high-level. You may, for example, consider an HTTP request like this:
POST /restaurants/90125/reservations?sig=aco7VV%2Bh5sA3RBtrN8zI8Y9kLKGC60Gm3SioZGosXVE%3D HTTP/1.1
Content-Type: application/json
{
"at": "2021-12-08 20:30",
"email": "snomob@example.com",
"name": "Snow Moe Beal",
"quantity": 1
}
Such an interaction implies a protocol. Part of such a protocol is that the HTTP request's body is a valid JSON document, that it has an at property, that that property encodes a valid date and time, that quantity is a natural number, that email is present, and so on.
You can model the expected input as a Data Transfer Object (DTO):
public sealed class ReservationDto { public string? At { get; set; } public string? Email { get; set; } public string? Name { get; set; } public int Quantity { get; set; } }
and even set up your 'protocol handlers' (here, an ASP.NET Core action method) to use such a DTO:
public Task<ActionResult> Post(ReservationDto dto)
While this may look statically typed, it assumes a particular protocol. What happens when the bytes on the wire don't follow the protocol?
Well, we've already been around that block more than once.
The point is that there's always an implied protocol at the application boundary, and you can choose to model it more or less explicitly.
Types as short-hands for protocols #
In the above example, I've relied on some static typing to deal with the problem. After all, I did define a DTO to model the expected shape of input. I could have chosen other alternatives: Perhaps I could have used a JSON parser to explicitly use the JSON DOM, or even more low-level used Utf8JsonReader. Ultimately, I could have decided to write my own JSON parser.
I'd rarely (or never?) choose to implement a JSON parser from scratch, so that's not what I'm advocating. Rather, my point is that you can leverage existing APIs to deal with input and output, and some of those APIs offer a convincing illusion that what happens at the boundary is statically typed.
This illusion is partly API-specific, and partly language-specific. In .NET, for example, JsonSerializer.Deserialize looks like it'll always deserialize any JSON string into the desired model. Obviously, that's a lie, because the function will throw an exception if the operation is impossible (i.e. when the input is malformed). In .NET (and many other languages or platforms), you can't tell from an API's type what the failure modes might be. In contrast, aeson's fromJSON function returns a type that explicitly indicates that deserialization may fail. Even in Haskell, however, this is mostly an idiomatic convention, because Haskell also 'supports' exceptions.
At the boundary, a static type can be a useful shorthand for a protocol. You declare a static type (e.g. a DTO) and rely on built-in machinery to handle malformed input. You give up some fine-grained control in exchange for a more declarative model.
I often choose to do that because I find such a trade-off beneficial, but I'm under no illusion that my static types fully model what goes 'on the wire'.
Reversed roles #
So far, I've mostly discussed input validation. Can types replace validation? No, but they can make most common validation scenarios easier. What happens when you return data?
You may decide to return a statically typed value. A serializer can faithfully convert such a value to a proper wire format (JSON, XML, or similar). The recipient may not care about that type. After all, you may return a Haskell value, but the system receiving the data is written in Python. Or you return a C# object, but the recipient is JavaScript.
Should we conclude, then, that there's no reason to model return data with static types? Not at all, because by modelling output with static types, you are being conservative with what you send. Since static types are typically more rigid than 'just code', there may be corner cases that a type can't easily express. While this may pose a problem when it comes to input, it's only a benefit when it comes to output. This means that you're narrowing the output funnel and thus making your system easier to work with.

Now consider another role-reversal: When your application initiates an interaction, it starts by producing output and receives input as a result. This includes any database interaction. When you create, update, or delete a row in a database, you send data, and receive a response.
Should you not consider Postel's law in that case?

Most people don't, particularly if they rely on object-relational mappers (ORMs). After all, if you have a static type (class) that models a database row, what's the harm using that when updating the database?
Probably none. After all, based on what I've just written, using a static type is a good way to be conservative with what you send. Here's an example using Entity Framework:
using var db = new RestaurantsContext(ConnectionString); var dbReservation = new Reservation { PublicId = reservation.Id, RestaurantId = restaurantId, At = reservation.At, Name = reservation.Name.ToString(), Email = reservation.Email.ToString(), Quantity = reservation.Quantity }; await db.Reservations.AddAsync(dbReservation); await db.SaveChangesAsync();
Here we send a statically typed Reservation 'Entity' to the database, and since we use a static type, we're being conservative with what we send. That's only good.
What happens when we query a database? Here's a typical example:
public async Task<Restaurants.Reservation?> ReadReservation(int restaurantId, Guid id) { using var db = new RestaurantsContext(ConnectionString); var r = await db.Reservations.FirstOrDefaultAsync(x => x.PublicId == id); if (r is null) return null; return new Restaurants.Reservation( r.PublicId, r.At, new Email(r.Email), new Name(r.Name), r.Quantity); }
Here I read a database row r and unquestioning translate it to my domain model. Should I do that? What if the database schema has diverged from my application code?
I suspect that much grief and trouble with relational databases, and particularly with ORMs, stem from the illusion that an ORM 'Entity' is a statically-typed view of the database schema. Typically, you can either use an ORM like Entity Framework in a code-first or a database-first fashion, but regardless of what you choose, you have two competing 'truths' about the database: The database schema and the Entity Classes.
You need to be disciplined to keep those two views in synch, and I'm not asserting that it's impossible. I'm only suggesting that it may pay to explicitly acknowledge that static types may not represent any truth about what's actually on the other side of the application boundary.
Types are an illusion #
Given that I usually find myself firmly in the static-types-are-great camp, it may seem odd that I now spend an entire article trashing them. Perhaps it looks as though I've had a revelation and made an about-face, but that's not the case. Rather, I'm fond of making the implicit explicit. This often helps improve understanding, because it helps delineate conceptual boundaries.
This, too, is the case here. All models are wrong, but some models are useful. So are static types, I believe.
A static type system is a useful tool that enables you to model how your application should behave. The types don't really exist at run time. Even though .NET code (just to point out an example) compiles to a binary representation that includes type information, once it runs, it JITs to machine code. In the end, it's just registers and memory addresses, or, if you want to be even more nihilistic, electrons moving around on a circuit board.
Even at a higher level of abstraction, you may say: But at least, a static type system can help you encapsulate rules and assumptions. In a language like C#, for example, consider a predicative type like this NaturalNumber class:
public struct NaturalNumber : IEquatable<NaturalNumber> { private readonly int i; public NaturalNumber(int candidate) { if (candidate < 1) throw new ArgumentOutOfRangeException( nameof(candidate), $"The value must be a positive (non-zero) number, but was: {candidate}."); this.i = candidate; } // Various other members follow...
Such a class effectively protects the invariant that a natural number is always a positive integer. Yes, that works well until someone does this:
var n = (NaturalNumber)FormatterServices.GetUninitializedObject(typeof(NaturalNumber));
This n value has the internal value 0. Yes, FormatterServices.GetUninitializedObject bypasses the constructor. This thing is evil, but it exists, and at least in the current discussion serves to illustrate the point that types are illusions.
This isn't just a flaw in C#. Other languages have similar backdoors. One of the most famously statically-typed languages, Haskell, comes with unsafePerformIO, which enables you to pretend that nothing untoward is going on even if you've written some impure code.
You may (and should) institute policies to not use such backdoors in your normal code bases. You don't need them.
Types are useful models #
All this may seem like an argument that types are useless. That would, however, be to draw the wrong conclusion. Types don't exist at run time to the same degree that Python objects or JavaScript functions don't exist at run time. Any language (except assembler) is an abstraction: A way to model computer instructions so that programming becomes easier (one would hope, but then...). This is true even for C, as low-level and detail-oriented as it may seem.
If you grant that high-level programming languages (i.e. any language that is not machine code or assembler) are useful, you must also grant that you can't rule out the usefulness of types. Notice that this argument is one of logic, rather than of preference. The only claim I make here is that programming is based on useful illusions. That the abstractions are illusions don't prevent them from being useful.
In statically typed languages, we effectively need to pretend that the type system is good enough, strong enough, generally trustworthy enough that it's safe to ignore the underlying reality. We work with, if you will, a provisional truth that serves as a user interface to the computer.
Even though a computer program eventually executes on a processor where types don't exist, a good compiler can still check that our models look sensible. We say that it type-checks. I find that indispensable when modelling the internal behaviour of a program. Even in a large code base, a compiler can type-check whether all the various components look like they may compose correctly. That a program compiles is no guarantee that it works correctly, but if it doesn't type-check, it's strong evidence that the code's model is internally inconsistent.
In other words, that a statically-typed program type-checks is a necessary, but not a sufficient condition for it to work.
This holds as long as we're considering program internals. Some language platforms allow us to take this notion further, because we can link software components together and still type-check them. The .NET platform is a good example of this, since the IL code retains type information. This means that the C#, F#, or Visual Basic .NET compiler can type-check your code against the APIs exposed by external libraries.
On the other hand, you can't extend that line of reasoning to the boundary of an application. What happens at the boundary is ultimately untyped.
Are types useless at the boundary, then? Not at all. Alexis King has already dealt with this topic better than I could, but the point is that types remain an effective way to capture the result of parsing input. You can view receiving, handling, parsing, or validating input as implementing a protocol, as I've already discussed above. Such protocols are application-specific or domain-specific rather than general-purpose protocols, but they are still protocols.
When I decide to write input validation for my restaurant sample code base as a set of composable parsers, I'm implementing a protocol. My starting point isn't raw bits, but rather a loose static type: A DTO. In other cases, I may decide to use a different level of abstraction.
One of the (many) reasons I have for finding ORMs unhelpful is exactly because they insist on an illusion past its usefulness. Rather, I prefer implementing the protocol that talks to my database with a lower-level API, such as ADO.NET:
private static Reservation ReadReservationRow(SqlDataReader rdr) { return new Reservation( (Guid)rdr["PublicId"], (DateTime)rdr["At"], new Email((string)rdr["Email"]), new Name((string)rdr["Name"]), new NaturalNumber((int)rdr["Quantity"])); }
This actually isn't a particular good protocol implementation, because it fails to take Postel's law into account. Really, this code should be a Tolerant Reader. In practice, not that much input contravariance is possible, but perhaps, at least, this code ought to gracefully handle if the Name field was missing.
The point of this particular example isn't that it's perfect, because it's not, but rather that it's possible to drop down to a lower level of abstraction, and sometimes, this may be a more honest representation of reality.
Conclusion #
It may be helpful to acknowledge that static types don't really exist. Even so, internally in a code base, a static type system can be a powerful tool. A good type system enables a compiler to check whether various parts of your code looks internally consistent. Are you calling a procedure with the correct arguments? Have you implemented all methods defined by an interface? Have you handled all cases defined by a sum type? Have you correctly initialized an object?
As useful type systems are for this kind of work, you should also be aware of their limitations. A compiler can check whether a code base's internal model makes sense, but it can't verify what happens at run time.
As long as one part of your code base sends data to another part of your code base, your type system can still perform a helpful sanity check, but for data that enters (or leaves) your application at run time, bets are off. You may attempt to model what input should look like, and it may even be useful to do that, but it's important to acknowledge that reality may not look like your model.
You can write statically-typed, composable parsers. Some of them are quite elegant, but the good ones explicitly model that parsing of input is error-prone. When input is well-formed, the result may be a nicely encapsulated, statically-typed value, but when it's malformed, the result is one or more error values.
Perhaps the most important message is that databases, other web services, file systems, etc. involve input and output, too. Even if you write code that initiates a database query, or a web service request, should you implicitly trust the data that comes back?
This question of trust doesn't have to imply security concerns. Rather, systems evolve and errors happen. Every time you interact with an external system, there's a risk that it has become misaligned with yours. Static types can't protect you against that.
What's a sandwich?
Ultimately, it's more about programming than food.
The Sandwich was named after John Montagu, 4th Earl of Sandwich because of his fondness for this kind of food. As popular story has it, he found it practical because it enabled him to eat without greasing the cards he often played.
A few years ago, a corner of the internet erupted in good-natured discussion about exactly what constitutes a sandwich. For instance, is the Danish smørrebrød a sandwich? It comes in two incarnations: Højtbelagt, the luxury version which is only consumable with knife and fork and the more modest, everyday håndmad (literally hand food), which, while open-faced, can usually be consumed without cutlery.

If we consider the 4th Earl of Sandwich's motivation as a yardstick, then the depicted højtbelagte smørrebrød is hardly a sandwich, while I believe a case can be made that a håndmad is:

Obviously, you need a different grip on a håndmad than on a sandwich. The bread (rugbrød) is much denser than wheat bread, and structurally more rigid. You eat it with your thumb and index finger on each side, and remaining fingers supporting it from below. The bottom line is this: A single piece of bread with something on top can also solve the original problem.
What if we go in the other direction? How about a combo consisting of bread, meat, bread, meat, and bread? I believe that I've seen burgers like that. Can you eat that with one hand? I think that this depends more on how greasy and overfilled it is, than on the structure.
What if you had five layers of meat and six layers of bread? This is unlikely to work with traditional Western leavened bread which, being a foam, will lose structural integrity when cut too thin. Imagining other kinds of bread, though, and thin slices of meat (or other 'content'), I don't see why it couldn't work.
FP sandwiches #
As regular readers may have picked up over the years, I do like food, but this is, after all, a programming blog.
A few years ago I presented a functional-programming design pattern named Impureim sandwich. It argues that it's often beneficial to structure a code base according to the functional core, imperative shell architecture.
The idea, in a nutshell, is that at every entry point (Main method, message handler, Controller action, etcetera) you first perform all impure actions necessary to collect input data for a pure function, then you call that pure function (which may be composed by many smaller functions), and finally you perform one or more impure actions based on the function's return value. That's the impure-pure-impure sandwich.
My experience with this pattern is that it's surprisingly often possible to apply it. Not always, but more often than you think.
Sometimes, however, it demands a looser interpretation of the word sandwich.
Even the examples from the article aren't standard sandwiches, once you dissect them. Consider, first, the Haskell example, here recoloured:
tryAcceptComposition :: Reservation -> IO (Maybe Int) tryAcceptComposition reservation = runMaybeT $ liftIO (DB.readReservations connectionString $ date reservation) >>= MaybeT . return . flip (tryAccept 10) reservation >>= liftIO . DB.createReservation connectionString
The date function is a pure accessor that retrieves the date and time of the reservation. In C#, it's typically a read-only property:
public async Task<IActionResult> Post(Reservation reservation) { return await Repository.ReadReservations(reservation.Date) .Select(rs => maîtreD.TryAccept(rs, reservation)) .SelectMany(m => m.Traverse(Repository.Create)) .Match(InternalServerError("Table unavailable"), Ok); }
Perhaps you don't think of a C# property as a function. After all, it's just an idiomatic grouping of language keywords:
public DateTimeOffset Date { get; }
Besides, a function takes input and returns output. What's the input in this case?
Keep in mind that a C# read-only property like this is only syntactic sugar for a getter method. In Java it would have been a method called getDate(). From Function isomorphisms we know that an instance method is isomorphic to a function that takes the object as input:
public static DateTimeOffset GetDate(Reservation reservation)
In other words, the Date property is an operation that takes the object itself as input and returns DateTimeOffset as output. The operation has no side effects, and will always return the same output for the same input. In other words, it's a pure function, and that's the reason I've now coloured it green in the above code examples.
The layering indicated by the examples may, however, be deceiving. The green colour of reservation.Date is adjacent to the green colour of the Select expression below it. You might interpret this as though the pure middle part of the sandwich partially expands to the upper impure phase.
That's not the case. The reservation.Date expression executes before Repository.ReadReservations, and only then does the pure Select expression execute. Perhaps this, then, is a more honest depiction of the sandwich:
public async Task<IActionResult> Post(Reservation reservation) { var date = reservation.Date; return await Repository.ReadReservations(date) .Select(rs => maîtreD.TryAccept(rs, reservation)) .SelectMany(m => m.Traverse(Repository.Create)) .Match(InternalServerError("Table unavailable"), Ok); }
The corresponding 'sandwich diagram' looks like this:

If you want to interpret the word sandwich narrowly, this is no longer a sandwich, since there's 'content' on top. That's the reason I started this article discussing Danish smørrebrød, also sometimes called open-faced sandwiches. Granted, I've never seen a håndmad with two slices of bread with meat both between and on top. On the other hand, I don't think that having a smidgen of 'content' on top is a showstopper.
Initial and eventual purity #
Why is this important? Whether or not reservation.Date is a little light of purity in the otherwise impure first slice of the sandwich actually doesn't concern me that much. After all, my concern is mostly cognitive load, and there's hardly much gained by extracting the reservation.Date expression to a separate line, as I did above.
The reason this interests me is that in many cases, the first step you may take is to validate input, and validation is a composed set of pure functions. While pure, and a solved problem, validation may be a sufficiently significant step that it warrants explicit acknowledgement. It's not just a property getter, but complex enough that bugs could hide there.
Even if you follow the functional core, imperative shell architecture, you'll often find that the first step is pure validation.
Likewise, once you've performed impure actions in the second impure phase, you can easily have a final thin pure translation slice. In fact, the above C# example contains an example of just that:
public IActionResult Ok(int value) { return new OkActionResult(value); } public IActionResult InternalServerError(string msg) { return new InternalServerErrorActionResult(msg); }
These are two tiny pure functions used as the final translation in the sandwich:
public async Task<IActionResult> Post(Reservation reservation) { var date = reservation.Date; return await Repository.ReadReservations(date) .Select(rs => maîtreD.TryAccept(rs, reservation)) .SelectMany(m => m.Traverse(Repository.Create)) .Match(InternalServerError("Table unavailable"), Ok); }
On the other hand, I didn't want to paint the Match operation green, since it's essentially a continuation of a Task, and if we consider task asynchronous programming as an IO surrogate, we should, at least, regard it with scepticism. While it might be pure, it probably isn't.
Still, we may be left with an inverted 'sandwich' that looks like this:

Can we still claim that this is a sandwich?
At the metaphor's limits #
This latest development seems to strain the sandwich metaphor. Can we maintain it, or does it fall apart?
What seems clear to me, at least, is that this ought to be the limit of how much we can stretch the allegory. If we add more tiers we get a Dagwood sandwich which is clearly a gimmick of little practicality.
But again, I'm appealing to a dubious metaphor, so instead, let's analyse what's going on.
In practice, it seems that you can rarely avoid the initial (pure) validation step. Why not? Couldn't you move validation to the functional core and do the impure steps without validation?
The short answer is no, because validation done right is actually parsing. At the entry point, you don't even know if the input makes sense.
A more realistic example is warranted, so I now turn to the example code base from my book Code That Fits in Your Head. One blog post shows how to implement applicative validation for posting a reservation.
A typical HTTP POST may include a JSON document like this:
{
"id": "bf4e84130dac451b9c94049da8ea8c17",
"at": "2024-11-07T20:30",
"email": "snomob@example.com",
"name": "Snow Moe Beal",
"quantity": 1
}
In order to handle even such a simple request, the system has to perform a set of impure actions. One of them is to query its data store for existing reservations. After all, the restaurant may not have any remaining tables for that day.
Which day, you ask? I'm glad you asked. The data access API comes with this method:
Task<IReadOnlyCollection<Reservation>> ReadReservations(
int restaurantId, DateTime min, DateTime max);
You can supply min and max values to indicate the range of dates you need. How do you determine that range? You need the desired date of the reservation. In the above example it's 20:30 on November 7 2024. We're in luck, the data is there, and understandable.
Notice, however, that due to limitations of wire formats such as JSON, the date is a string. The value might be anything. If it's sufficiently malformed, you can't even perform the impure action of querying the database, because you don't know what to query it about.
If keeping the sandwich metaphor untarnished, you might decide to push the parsing responsibility to an impure action, but why make something impure that has a well-known pure solution?
A similar argument applies when performing a final, pure translation step in the other direction.
So it seems that we're stuck with implementations that don't quite fit the ideal of the sandwich metaphor. Is that enough to abandon the metaphor, or should we keep it?
The layers in layered application architecture aren't really layers, and neither are vertical slices really slices. All models are wrong, but some are useful. This is the case here, I believe. You should still keep the Impureim sandwich in mind when structuring code: Keep impure actions at the application boundary - in the 'Controllers', if you will; have only two phases of impurity - the initial and the ultimate; and maximise use of pure functions for everything else. Keep most of the pure execution between the two impure phases, but realistically, you're going to need a pure validation phase in front, and a slim translation layer at the end.
Conclusion #
Despite the prevalence of food imagery, this article about functional programming architecture has eluded any mention of burritos. Instead, it examines the tension between an ideal, the Impureim sandwich, with real-world implementation details. When you have to deal with concerns such as input validation or translation to egress data, it's practical to add one or two more thin slices of purity.
In functional architecture you want to maximise the proportion of pure functions. Adding more pure code is hardly a problem.
The opposite is not the case. We shouldn't be cavalier about adding more impure slices to the sandwich. Thus, the adjusted definition of the Impureim sandwich seems to be that it may have at most two impure phases, but from one to three pure slices.
Comments
Hello again...
In one of your excellent talks (here), you ended up refactoring maitreD kata using the
traversefunction. Since this step is crucial for "sandwich" to work, any post detailing it's implementation would be nice.
Thanks
qfilip, thank you for writing. That particular talk fortunately comes with a set of companion articles:
The latter of the two comes with a link to a GitHub repository with all the sample code, including the Traverse implementation.
That said, a more formal description of traversals has long been on my to-do list, as you can infer from this (currently inactive) table of contents.
Dependency Whac-A-Mole
AKA Framework Whac-A-Mole, Library Whac-A-Mole.
I have now three times used the name Whac-A-Mole about a particular kind of relationship that may evolve with some dependencies. According to the rule of three, I can now extract the explanation to a separate article. This is that article.
Architecture smell #
Dependency Whac-A-Mole describes the situation when you're spending too much time investigating, learning, troubleshooting, and overall satisfying the needs of a dependency (i.e. library or framework) instead of delivering value to users.
Examples include Dependency Injection containers, object-relational mappers, validation frameworks, dynamic mock libraries, and perhaps the Gherkin language.
From the above list it does not follow that those examples are universally bad. I can think of situations where some of them make sense. I might even use them myself.
Rather, the Dependency Whac-A-Mole architecture smell occurs when a given dependency causes more trouble than the benefit it was supposed to provide.
Causes #
We rarely set out to do the wrong thing, but we often make mistakes in good faith. You may decide to take a dependency on a library or framework because
- it worked well for you in a previous context
- it looks as though it'll address a major problem you had in a previous context
- you've heard good things about it
- you saw a convincing demo
- you heard about it in a podcast, conference talk, YouTube video, etc.
- a FAANG company uses it
- it's the latest tech
- you want it on your CV
There could be other motivations as well, and granted, some of those I listed aren't really good reasons. Even so, I don't think anyone chooses a dependency with ill intent.
And what might work in one context may turn out to not work in another. You can't always predict such consequences, so I imply no judgement on those who choose the 'wrong' dependency. I've done it, too.
It is, however, important to be aware that this risk is always there. You picked a library with the best of intentions, but it turns out to slow you down. If so, acknowledge the mistake and kill your darlings.
Background #
Whenever you use a library or framework, you need to learn how to use it effectively. You have to learn its concepts, abstractions, APIs, pitfalls, etc. Not only that, but you need to stay abreast of changes and improvements.
Microsoft, for example, is usually good at maintaining backwards compatibility, but even so, things don't stand still. They evolve libraries and frameworks the same way I would do it: Don't introduce breaking changes, but do introduce new, better APIs going forward. This is essentially the Strangler pattern that I also write about in Code That Fits in Your Head.
While it's a good way to evolve a library or framework, the point remains: Even if you trust a supplier to prioritise backwards compatibility, it doesn't mean that you can stop learning. You have to stay up to date with all your dependencies. If you don't, sooner or later, the way that you use something like, say, Entity Framework is 'the old way', and it's not really supported any longer.
In order to be able to move forward, you'll have to rewrite those parts of your code that depend on that old way of doing things.
Each dependency comes with benefits and costs. As long as the benefits outweigh the costs, it makes sense to keep it around. If, on the other hand, you spend more time dealing with it than it would take you to do the work yourself, consider getting rid of it.
Symptoms #
Perhaps the infamous left-pad incident is too easy an example, but it does highlight the essence of this tension. Do you really need a third-party package to pad a string, or could you have done it yourself?
You can spend much time figuring out how to fit a general-purpose library or framework to your particular needs. How do you make your object-relational mapper (ORM) fit a special database schema? How do you annotate a class so that it produces validation messages according to the requirements in your jurisdiction? How do you configure an automatic mapping library so that it correctly projects data? How do you tell a Dependency Injection (DI) Container how to compose a Chain of Responsibility where some objects also take strings or integers in their constructors?
Do such libraries or frameworks save time, or could you have written the corresponding code quicker? To be clear, I'm not talking about writing your own ORM, your own DI Container, your own auto-mapper. Rather, instead of using a DI Container, Pure DI is likely easier. As an alternative to an ORM, what's the cost of just writing SQL? Instead of an ad-hoc, informally-specified, bug-ridden validation framework, have you considered applicative validation?
Things become really insidious if your chosen library never really solves all problems. Every time you figure out how to use it for one exotic corner case, your 'solution' causes a new problem to arise.
A symptom of Dependency Whac-A-Mole is when you have to advertise after people skilled in a particular technology.
Again, it's not necessarily a problem. If you're getting tremendous value out of, say, Entity Framework, it makes sense to list expertise as a job requirement. If, on the other hand, you have to list a litany of libraries and frameworks as necessary skills, it might pay to stop and reconsider. You can call it your 'tech stack' all you will, but is it really an inadvertent case of vendor lock-in?
Anecdotal evidence #
I've used the term Whac-A-Mole a couple of times to describe the kind of situation where you feel that you're fighting a technology more than it's helping you. It seems to resonate with other people than me.
Here are the original articles where I used the term:
These are only the articles where I explicitly use the term. I do, however, think that the phenomenon is more common. I'm particularly sensitive to it when it comes to Dependency Injection, where I generally believe that DI Containers make the technique harder that it has to be. Composing object graphs is easily done with code.
Conclusion #
Sometimes a framework or library makes it more difficult to get things done. You spend much time kowtowing to its needs, researching how to do things 'the xyz way', learning its intricate extensibility points, keeping up to date with its evolving API, and engaging with its community to lobby for new features.
Still, you feel that it makes you compromise. You might have liked to organise your code in a different way, but unfortunately you can't, because it doesn't fit the way the dependency works. As you solve issues with it, new ones appear.
These are symptoms of Dependency Whac-A-Mole, an architecture smell that indicates that you're using the wrong tool for the job. If so, get rid of the dependency in favour of something better. Often, the better alternative is just plain vanilla code.
Comments
The most obvious example of this for me is definitely AutoMapper. I used to think it was great and saved so much time, but more often than not, the mapping configuration ended up being more complex (and fragile) than just mapping the properties manually.
I could imagine. AutoMapper is not, however, a library I've used enough to evaluate.
The moment I lost any faith in AutoMapper was after trying to debug a mapping that was silently failing on a single property. Three of us were looking at it for a good amount of time before one of us noticed a single character typo on the destination property. As the names did not match, no mapping occurred. It is unfortunately a black box, and obfuscated a problem that a manual mapping would have handled gracefully.
Mark, it is interesting that you mention Gherkin as potentially one of these moles. It is something I've been evaluating in the hopes of making our tests more business focused, but considering it again now, you can achieve a lot of what Gherkin offers with well defined namespaces, classes and methods in your test assemblies, something like:
- Namespace: GivenSomePrecondition
- TestClass: WhenCarryingOutAnAction
- TestMethod: ThenTheExpectedPostConditionResults
Callum, I was expecting someone to comment on including Gherkin on the list.
I don't consider all my examples as universally problematic. Rather, they often pop up in contexts where people seem to be struggling with a concept or a piece of technology with no apparent benefit.
I'm sure that when Dan North came up with the idea of BDD and Gherkin, he actually used it. When used in the way it was originally intended, I can see it providing value.
Apart from Dan himself, however, I'm not aware that I've ever met anyone who has used BDD and Gherkin in that way. On the contrary, I've had more than one discussion that went like this:
Interlocutor: "We use BDD and Gherkin. It's great! You should try it."
Me: "Why?"
Interlocutor: "It enables us to organise our tests."
Me: "Can't you do that with the AAA pattern?"
Interlocutor: "..."
Me: "Do any non-programmers ever look at your tests?"
Interlocutor: "No..."
If only programmers look at the test code, then why impose an artificial constraint? Given-when-then is just arrange-act-assert with different names, but free of Gherkin and the tooling that typically comes with it, you're free to write test code that follows normal good coding practices.
(As an aside, yes: Sometimes constraints liberate, but what I've seen of Gherkin-based test code, this doesn't seem to be one of those cases.)
Finally, to be quite clear, although I may be repeating myself: If you're using Gherkin to interact with non-programmers on a regular basis, it may be beneficial. I've just never been in that situation, or met anyone other than Dan North who have.
The case of the mysterious comparison
A ploeh mystery.
I was recently playing around with the example code from my book Code That Fits in Your Head, refactoring the Table class to use a predicative NaturalNumber wrapper to represent a table's seating capacity.
Originally, the Table constructor and corresponding read-only data looked like this:
private readonly bool isStandard; private readonly Reservation[] reservations; public int Capacity { get; } private Table(bool isStandard, int capacity, params Reservation[] reservations) { this.isStandard = isStandard; Capacity = capacity; this.reservations = reservations; }
Since I wanted to show an example of how wrapper types can help make preconditions explicit, I changed it to this:
private readonly bool isStandard; private readonly Reservation[] reservations; public NaturalNumber Capacity { get; } private Table(bool isStandard, NaturalNumber capacity, params Reservation[] reservations) { this.isStandard = isStandard; Capacity = capacity; this.reservations = reservations; }
The only thing I changed was the type of Capacity and capacity.
As I did that, two tests failed.
Evidence #
Both tests failed in the same way, so I only show one of the failures:
Ploeh.Samples.Restaurants.RestApi.Tests.MaitreDScheduleTests.Schedule Source: MaitreDScheduleTests.cs line 16 Duration: 340 ms Message: FsCheck.Xunit.PropertyFailedException : Falsifiable, after 2 tests (0 shrinks) (StdGen (48558275,297233133)): Original: <null> (Ploeh.Samples.Restaurants.RestApi.MaitreD, [|Ploeh.Samples.Restaurants.RestApi.Reservation|]) ---- System.InvalidOperationException : Failed to compare two elements in the array. -------- System.ArgumentException : At least one object must implement IComparable. Stack Trace: ----- Inner Stack Trace ----- GenericArraySortHelper`1.Sort(T[] keys, Int32 index, Int32 length, IComparer`1 comparer) Array.Sort[T](T[] array, Int32 index, Int32 length, IComparer`1 comparer) EnumerableSorter`2.QuickSort(Int32[] keys, Int32 lo, Int32 hi) EnumerableSorter`1.Sort(TElement[] elements, Int32 count) OrderedEnumerable`1.ToList() Enumerable.ToList[TSource](IEnumerable`1 source) MaitreD.Allocate(IEnumerable`1 reservations) line 91 <>c__DisplayClass21_0.<Schedule>b__4(<>f__AnonymousType7`2 <>h__TransparentIdentifier1) line 114 <>c__DisplayClass2_0`3.<CombineSelectors>b__0(TSource x) SelectIPartitionIterator`2.GetCount(Boolean onlyIfCheap) Enumerable.Count[TSource](IEnumerable`1 source) MaitreDScheduleTests.ScheduleImp(MaitreD sut, Reservation[] reservations) line 31 <>c.<Schedule>b__0_2(ValueTuple`2 t) line 22 ForAll@15.Invoke(Value arg00) Testable.evaluate[a,b](FSharpFunc`2 body, a a) ----- Inner Stack Trace ----- Comparer.Compare(Object a, Object b) ObjectComparer`1.Compare(T x, T y) EnumerableSorter`2.CompareAnyKeys(Int32 index1, Int32 index2) ComparisonComparer`1.Compare(T x, T y) ArraySortHelper`1.SwapIfGreater(T[] keys, Comparison`1 comparer, Int32 a, Int32 b) ArraySortHelper`1.IntroSort(T[] keys, Int32 lo, Int32 hi, Int32 depthLimit, Comparison`1 comparer) GenericArraySortHelper`1.Sort(T[] keys, Int32 index, Int32 length, IComparer`1 comparer)
The code highlighted with red is user code (i.e. my code). The rest comes from .NET or FsCheck.
While a stack trace like that can look intimidating, I usually navigate to the top stack frame of my own code. As I reproduce my investigation, see if you can spot the problem before I did.
Understand before resolving #
Before starting the investigation proper, we might as well acknowledge what seems evident. I had a fully passing test suite, then I edited two lines of code, which caused the above error. The two nested exception messages contain obvious clues: Failed to compare two elements in the array, and At least one object must implement IComparable.
The only edit I made was to change an int to a NaturalNumber, and NaturalNumber didn't implement IComparable. It seems straightforward to just make NaturalNumber implement that interface and move on, and as it turns out, that is the solution.
As I describe in Code That Fits in Your Head, when troubleshooting, first seek to understand the problem. I've seen too many people go immediately into 'action mode' when faced with a problem. It's often a suboptimal strategy.
First, if the immediate solution turns out not to work, you can waste much time trashing, trying various 'fixes' without understanding the problem.
Second, even if the resolution is easy, as is the case here, if you don't understand the underlying cause and effect, you can easily build a cargo cult-like 'understanding' of programming. This could become one such experience: All wrapper types must implement IComparable, or some nonsense like that.
Unless people are getting hurt or you are bleeding money because of the error, seek first to understand, and only then fix the problem.
First clue #
The top user stack frame is the Allocate method:
private IEnumerable<Table> Allocate( IEnumerable<Reservation> reservations) { List<Table> allocation = Tables.ToList(); foreach (var r in reservations) { var table = allocation.Find(t => t.Fits(r.Quantity)); if (table is { }) { allocation.Remove(table); allocation.Add(table.Reserve(r)); } } return allocation; }
The stack trace points to line 91, which is the first line of code; where it calls Tables.ToList(). This is also consistent with the stack trace, which indicates that the exception is thrown from ToList.
I am, however, not used to ToList throwing exceptions, so I admit that I was nonplussed. Why would ToList try to sort the input? It usually doesn't do that.
Now, I did notice the OrderedEnumerable`1 on the stack frame above Enumerable.ToList, but this early in the investigation, I failed to connect the dots.
What does the caller look like? It's that scary DisplayClass21...
Immediate caller #
The code that calls Allocate is the Schedule method, the System Under Test:
public IEnumerable<TimeSlot> Schedule( IEnumerable<Reservation> reservations) { return from r in reservations group r by r.At into g orderby g.Key let seating = new Seating(SeatingDuration, g.Key) let overlapping = reservations.Where(seating.Overlaps) select new TimeSlot(g.Key, Allocate(overlapping).ToList()); }
While it does orderby, it doesn't seem to be sorting the input to Allocate. While overlapping is a filtered subset of reservations, the code doesn't sort reservations.
Okay, moving on, what does the caller of that method look like?
Test implementation #
The caller of the Schedule method is this test implementation:
private static void ScheduleImp( MaitreD sut, Reservation[] reservations) { var actual = sut.Schedule(reservations); Assert.Equal( reservations.Select(r => r.At).Distinct().Count(), actual.Count()); Assert.Equal( actual.Select(ts => ts.At).OrderBy(d => d), actual.Select(ts => ts.At)); Assert.All(actual, ts => AssertTables(sut.Tables, ts.Tables)); Assert.All( actual, ts => AssertRelevance(reservations, sut.SeatingDuration, ts)); }
Notice how the first line of code calls Schedule, while the rest is 'just' assertions.
Because I had noticed that OrderedEnumerable`1 on the stack, I was on the lookout for an expression that would sort an IEnumerable<T>. The ScheduleImp method surprised me, though, because the reservations parameter is an array. If there was any problem sorting it, it should have blown up much earlier.
I really should be paying more attention, but despite my best resolution to proceed methodically, I was chasing the wrong clue.
Which line of code throws the exception? The stack trace says line 31. That's not the sut.Schedule(reservations) call. It's the first assertion following it. I failed to notice that.
Property #
I was stumped, and not knowing what to do, I looked at the fourth and final piece of user code in that stack trace:
[Property] public Property Schedule() { return Prop.ForAll( (from rs in Gens.Reservations from m in Gens.MaitreD(rs) select (m, rs)).ToArbitrary(), t => ScheduleImp(t.m, t.rs)); }
No sorting there. What's going on?
In retrospect, I'm struggling to understand what was going on in my mind. Perhaps you're about to lose patience with me. I was chasing the wrong 'clue', just as I said above that 'other' people do, but surely, it's understood, that I don't.
WYSIATI #
In Code That Fits in Your Head I spend some time discussing how code relates to human cognition. I'm no neuroscientist, but I try to read books on other topics than programming. I was partially inspired by Thinking, Fast and Slow in which Daniel Kahneman (among many other topics) presents how System 1 (the inaccurate fast thinking process) mostly works with what's right in front of it: What You See Is All There Is, or WYSIATI.
That OrderedEnumerable`1 in the stack trace had made me look for an IEnumerable<T> as the culprit, and in the source code of the Allocate method, one parameter is clearly what I was looking for. I'll repeat that code here for your benefit:
private IEnumerable<Table> Allocate( IEnumerable<Reservation> reservations) { List<Table> allocation = Tables.ToList(); foreach (var r in reservations) { var table = allocation.Find(t => t.Fits(r.Quantity)); if (table is { }) { allocation.Remove(table); allocation.Add(table.Reserve(r)); } } return allocation; }
Where's the IEnumerable<T> in that code?
reservations, right?
Revelation #
As WYSIATI 'predicts', the brain gloms on to what's prominent. I was looking for IEnumerable<T>, and it's right there in the method declaration as the parameter IEnumerable<Reservation> reservations.
As covered in multiple places (my book, The Programmer's Brain), the human brain has limited short-term memory. Apparently, while chasing the IEnumerable<T> clue, I'd already managed to forget another important datum.
Which line of code throws the exception? This one:
List<Table> allocation = Tables.ToList();
The IEnumerable<T> isn't reservations, but Tables.
While the code doesn't explicitly say IEnumerable<Table> Tables, that's just what it is.
Yes, it took me way too long to notice that I'd been barking up the wrong tree all along. Perhaps you immediately noticed that, but have pity with me. I don't think this kind of human error is uncommon.
The culprit #
Where do Tables come from? It's a read-only property originally injected via the constructor:
public MaitreD( TimeOfDay opensAt, TimeOfDay lastSeating, TimeSpan seatingDuration, IEnumerable<Table> tables) { OpensAt = opensAt; LastSeating = lastSeating; SeatingDuration = seatingDuration; Tables = tables; }
Okay, in the test then, where does it come from? That's the m in the above property, repeated here for your convenience:
[Property] public Property Schedule() { return Prop.ForAll( (from rs in Gens.Reservations from m in Gens.MaitreD(rs) select (m, rs)).ToArbitrary(), t => ScheduleImp(t.m, t.rs)); }
The m variable is generated by Gens.MaitreD, so let's follow that clue:
internal static Gen<MaitreD> MaitreD( IEnumerable<Reservation> reservations) { return from seatingDuration in Gen.Choose(1, 6) from tables in Tables(reservations) select new MaitreD( TimeSpan.FromHours(18), TimeSpan.FromHours(21), TimeSpan.FromHours(seatingDuration), tables); }
We're not there yet, but close. The tables variable is generated by this Tables helper function:
/// <summary> /// Generate a table configuration that can at minimum accomodate all /// reservations. /// </summary> /// <param name="reservations">The reservations to accommodate</param> /// <returns>A generator of valid table configurations.</returns> private static Gen<IEnumerable<Table>> Tables( IEnumerable<Reservation> reservations) { // Create a table for each reservation, to ensure that all // reservations can be allotted a table. var tables = reservations.Select(r => Table.Standard(r.Quantity)); return from moreTables in Gen.Choose(1, 12).Select( i => Table.Standard(new NaturalNumber(i))).ArrayOf() let allTables = tables.Concat(moreTables).OrderBy(t => t.Capacity) select allTables.AsEnumerable(); }
And there you have it: OrderBy(t => t.Capacity)!
The Capacity property was exactly the property I changed from int to NaturalNumber - the change that made the test fail.
As expected, the fix was to let NaturalNumber implement IComparable<NaturalNumber>.
Conclusion #
I thought this little troubleshooting session was interesting enough to write down. I spent perhaps twenty minutes on it before I understood what was going on. Not disastrously long, but enough time that I was relieved when I figured it out.
Apart from the obvious (look for the problem where it is), there is one other useful lesson to be learned, I think.
Deferred execution can confuse even the most experienced programmer. It took me some time before it dawned on me that even though the the MaitreD constructor had run and the object was 'safely' initialised, it actually wasn't.
The implication is that there's a 'disconnect' between the constructor and the Allocate method. The error actually happens during initialisation (i.e. in the caller of the constructor), but it only manifests when you run the method.
Ever since I discovered the IReadOnlyCollection<T> interface in 2013 I've resolved to favour it over IEnumerable<T>. This is one example of why that's a good idea.
Despite my best intentions, I, too, cut corners from time to time. I've done it here, by accepting IEnumerable<Table> instead of IReadOnlyCollection<Table> as a constructor parameter. I really should have known better, and now I've paid the price.
This is particularly ironic because I also love Haskell so much. Haskell is lazy by default, so you'd think that I run into such issues all the time. An expression like OrderBy(t => t.Capacity), however, wouldn't have compiled in Haskell unless the sort key implemented the Ord type class. Even C#'s type system can express that a generic type must implement an interface, but OrderBy doesn't do that.
This problem could have been caught at compile-time, but unfortunately it wasn't.
Comments
I made a pull request describing the issue.
As this is likely a breaking change I don't have high hopes for it to be fixed, though…
Do ORMs reduce the need for mapping?
With some Entity Framework examples in C#.
In a recent comment, a reader asked me to expand on my position on object-relational mappers (ORMs), which is that I'm not a fan:
I consider ORMs a waste of time: they create more problems than they solve.
While I acknowledge that only a Sith deals in absolutes, I favour clear assertions over guarded language. I don't really mean it that categorically, but I do stand by the general sentiment. In this article I'll attempt to describe why I don't reach for ORMs when querying or writing to a relational database.
As always, any exploration of such a kind is made in a context, and this article is no exception. Before proceeding, allow me to delineate the scope. If your context differs from mine, what I write may not apply to your situation.
Scope #
It's been decades since I last worked on a system where the database 'came first'. The last time that happened, the database was hidden behind an XML-based RPC API that tunnelled through HTTP. Not a REST API by a long shot.
Since then, I've worked on various systems. Some used relational databases, some document databases, some worked with CSV, or really old legacy APIs, etc. Common to these systems was that they were not designed around a database. Rather, they were developed with an eye to the Dependency Inversion Principle, keeping storage details out of the Domain Model. Many were developed with test-driven development (TDD).
When I evaluate whether or not to use an ORM in situations like these, the core application logic is my main design driver. As I describe in Code That Fits in Your Head, I usually develop (vertical) feature slices one at a time, utilising an outside-in TDD process, during which I also figure out how to save or retrieve data from persistent storage.
Thus, in systems like these, storage implementation is an artefact of the software architecture. If a relational database is involved, the schema must adhere to the needs of the code; not the other way around.
To be clear, then, this article doesn't discuss typical CRUD-heavy applications that are mostly forms over relational data, with little or no application logic. If you're working with such a code base, an ORM might be useful. I can't really tell, since I last worked with such systems at a time when ORMs didn't exist.
The usual suspects #
The most common criticism of ORMs (that I've come across) is typically related to the queries they generate. People who are skilled in writing SQL by hand, or who are concerned about performance, may look at the SQL that an ORM generates and dislike it for that reason.
It's my impression that ORMs have come a long way over the decades, but frankly, the generated SQL is not really what concerns me. It never was.
In the abstract, Ted Neward already outlined the problems in the seminal article The Vietnam of Computer Science. That problem description may, however, be too theoretical to connect with most programmers, so I'll try a more example-driven angle.
Database operations without an ORM #
Once more I turn to the trusty example code base that accompanies Code That Fits in Your Head. In it, I used SQL Server as the example database, and ADO.NET as the data access technology.
I considered this more than adequate for saving and reading restaurant reservations. Here, for example, is the code that creates a new reservation row in the database:
public async Task Create(int restaurantId, Reservation reservation) { if (reservation is null) throw new ArgumentNullException(nameof(reservation)); using var conn = new SqlConnection(ConnectionString); using var cmd = new SqlCommand(createReservationSql, conn); cmd.Parameters.AddWithValue("@Id", reservation.Id); cmd.Parameters.AddWithValue("@RestaurantId", restaurantId); cmd.Parameters.AddWithValue("@At", reservation.At); cmd.Parameters.AddWithValue("@Name", reservation.Name.ToString()); cmd.Parameters.AddWithValue("@Email", reservation.Email.ToString()); cmd.Parameters.AddWithValue("@Quantity", reservation.Quantity); await conn.OpenAsync().ConfigureAwait(false); await cmd.ExecuteNonQueryAsync().ConfigureAwait(false); } private const string createReservationSql = @" INSERT INTO [dbo].[Reservations] ( [PublicId], [RestaurantId], [At], [Name], [Email], [Quantity]) VALUES (@Id, @RestaurantId, @At, @Name, @Email, @Quantity)";
Yes, there's mapping, even if it's 'only' from a Domain Object to command parameter strings. As I'll argue later, if there's a way to escape such mapping, I'm not aware of it. ORMs don't seem to solve that problem.
This, however, seems to be the reader's main concern:
"I can work with raw SQL ofcourse... but the mapping... oh the mapping..."
It's not a concern that I share, but again I'll remind you that if your context differs substantially from mine, what doesn't concern me could reasonably concern you.
You may argue that the above example isn't representative, since it only involves a single table. No foreign key relationships are involved, so perhaps the example is artificially easy.
In order to work with a slightly more complex schema, I decided to port the read-only in-memory restaurant database (the one that keeps track of the restaurants - the tenants - of the system) to SQL Server.
Restaurants schema #
In the book's sample code base, I'd only stored restaurant configurations as JSON config files, since I considered it out of scope to include an online tenant management system. Converting to a relational model wasn't hard, though. Here's the database schema:
CREATE TABLE [dbo].[Restaurants] ( [Id] INT NOT NULL, [Name] NVARCHAR (50) NOT NULL UNIQUE, [OpensAt] TIME NOT NULL, [LastSeating] TIME NOT NULL, [SeatingDuration] TIME NOT NULL PRIMARY KEY CLUSTERED ([Id] ASC) ) CREATE TABLE [dbo].[Tables] ( [Id] INT NOT NULL IDENTITY, [RestaurantId] INT NOT NULL REFERENCES [dbo].[Restaurants](Id), [Capacity] INT NOT NULL, [IsCommunal] BIT NOT NULL PRIMARY KEY CLUSTERED ([Id] ASC) )
This little subsystem requires two database tables: One that keeps track of the overall restaurant configuration, such as name, opening and closing times, and another database table that lists all a restaurant's physical tables.
You may argue that this is still too simple to realistically capture the intricacies of existing database systems, but conversely I'll remind you that the scope of this article is the sort of system where you develop and design the application first; not a system where you're given a relational database upon which you must create an application.
Had I been given this assignment in a realistic setting, a relational database probably wouldn't have been my first choice. Some kind of document database, or even blob storage, strikes me as a better fit. Still, this article is about ORMs, so I'll pretend that there are external circumstances that dictate a relational database.
To test the system, I also created a script to populate these tables. Here's part of it:
INSERT INTO [dbo].[Restaurants] ([Id], [Name], [OpensAt], [LastSeating], [SeatingDuration]) VALUES (1, N'Hipgnosta', '18:00', '21:00', '6:00') INSERT INTO [dbo].[Tables] ([RestaurantId], [Capacity], [IsCommunal]) VALUES (1, 10, 1) INSERT INTO [dbo].[Restaurants] ([Id], [Name], [OpensAt], [LastSeating], [SeatingDuration]) VALUES (2112, N'Nono', '18:00', '21:00', '6:00') INSERT INTO [dbo].[Tables] ([RestaurantId], [Capacity], [IsCommunal]) VALUES (2112, 6, 1) INSERT INTO [dbo].[Tables] ([RestaurantId], [Capacity], [IsCommunal]) VALUES (2112, 4, 1) INSERT INTO [dbo].[Tables] ([RestaurantId], [Capacity], [IsCommunal]) VALUES (2112, 2, 0) INSERT INTO [dbo].[Tables] ([RestaurantId], [Capacity], [IsCommunal]) VALUES (2112, 2, 0) INSERT INTO [dbo].[Tables] ([RestaurantId], [Capacity], [IsCommunal]) VALUES (2112, 4, 0) INSERT INTO [dbo].[Tables] ([RestaurantId], [Capacity], [IsCommunal]) VALUES (2112, 4, 0)
There are more rows than this, but this should give you an idea of what data looks like.
Reading restaurant data without an ORM #
Due to the foreign key relationship, reading restaurant data from the database is a little more involved than reading from a single table.
public async Task<Restaurant?> GetRestaurant(string name) { using var cmd = new SqlCommand(readByNameSql); cmd.Parameters.AddWithValue("@Name", name); var restaurants = await ReadRestaurants(cmd); return restaurants.SingleOrDefault(); } private const string readByNameSql = @" SELECT [Id], [Name], [OpensAt], [LastSeating], [SeatingDuration] FROM [dbo].[Restaurants] WHERE [Name] = @Name SELECT [RestaurantId], [Capacity], [IsCommunal] FROM [dbo].[Tables] JOIN [dbo].[Restaurants] ON [dbo].[Tables].[RestaurantId] = [dbo].[Restaurants].[Id] WHERE [Name] = @Name";
There are more than one option when deciding how to construct the query. You could make one query with a join, in which case you'd get rows with repeated data, and you'd then need to detect duplicates, or you could do as I've done here: Query each table to get multiple result sets.
I'm not claiming that this is better in any way. I only chose this option because I found the code that I had to write less offensive.
Since the IRestaurantDatabase interface defines three different kinds of queries (GetAll(), GetRestaurant(int id), and GetRestaurant(string name)), I invoked the rule of three and extracted a helper method:
private async Task<IEnumerable<Restaurant>> ReadRestaurants(SqlCommand cmd) { var conn = new SqlConnection(ConnectionString); cmd.Connection = conn; await conn.OpenAsync(); using var rdr = await cmd.ExecuteReaderAsync(); var restaurants = Enumerable.Empty<Restaurant>(); while (await rdr.ReadAsync()) restaurants = restaurants.Append(ReadRestaurantRow(rdr)); if (await rdr.NextResultAsync()) while (await rdr.ReadAsync()) restaurants = ReadTableRow(rdr, restaurants); return restaurants; }
The ReadRestaurants method does the overall work of opening the database connection, executing the query, and moving through rows and result sets. Again, we'll find mapping code hidden in helper methods:
private static Restaurant ReadRestaurantRow(SqlDataReader rdr) { return new Restaurant( (int)rdr["Id"], (string)rdr["Name"], new MaitreD( new TimeOfDay((TimeSpan)rdr["OpensAt"]), new TimeOfDay((TimeSpan)rdr["LastSeating"]), (TimeSpan)rdr["SeatingDuration"])); }
As the name suggests, ReadRestaurantRow reads a row from the Restaurants table and converts it into a Restaurant object. At this time, however, it creates each MaitreD object without any tables. This is possible because one of the MaitreD constructors takes a params array as the last parameter:
public MaitreD( TimeOfDay opensAt, TimeOfDay lastSeating, TimeSpan seatingDuration, params Table[] tables) : this(opensAt, lastSeating, seatingDuration, tables.AsEnumerable()) { }
Only when the ReadRestaurants method moves on to the next result set can it add tables to each restaurant:
private static IEnumerable<Restaurant> ReadTableRow( SqlDataReader rdr, IEnumerable<Restaurant> restaurants) { var restaurantId = (int)rdr["RestaurantId"]; var capacity = (int)rdr["Capacity"]; var isCommunal = (bool)rdr["IsCommunal"]; var table = isCommunal ? Table.Communal(capacity) : Table.Standard(capacity); return restaurants.Select(r => r.Id == restaurantId ? AddTable(r, table) : r); }
As was also the case in ReadRestaurantRow, this method uses string-based indexers on the rdr to extract the data. I'm no fan of stringly-typed code, but at least I have automated tests that exercise these methods.
Could an ORM help by creating strongly-typed classes that model database tables? To a degree; I'll discuss that later.
In any case, since the entire code base follows the Functional Core, Imperative Shell architecture, the entire Domain Model is made of immutable data types with pure functions. Thus, ReadTableRow has to iterate over all restaurants and add the table when the Id matches. AddTable does that:
private static Restaurant AddTable(Restaurant restaurant, Table table) { return restaurant.Select(m => m.WithTables(m.Tables.Append(table).ToArray())); }
I can think of other ways to solve the overall mapping task when using ADO.NET, but this was what made most sense to me.
Reading restaurants with Entity Framework #
Does an ORM like Entity Framework (EF) improve things? To a degree, but not enough to outweigh the disadvantages it also brings.
In order to investigate, I followed the EF documentation to scaffold code from a database I'd set up for only that purpose. For the Tables table it created the following Table class and a similar Restaurant class.
public partial class Table { public int Id { get; set; } public int RestaurantId { get; set; } public int Capacity { get; set; } public bool IsCommunal { get; set; } public virtual Restaurant Restaurant { get; set; } = null!; }
Hardly surprising. Also, hardly object-oriented, but more about that later, too.
Entity Framework didn't, by itself, add a Tables collection to the Restaurant class, so I had to do that by hand, as well as modify the DbContext-derived class to tell it about this relationship:
entity.OwnsMany(r => r.Tables, b => { b.Property<int>(t => t.Id).ValueGeneratedOnAdd(); b.HasKey(t => t.Id); });
I thought that such a simple foreign key relationship would be something an ORM would help with, but apparently not.
With that in place, I could now rewrite the above GetRestaurant method to use Entity Framework instead of ADO.NET:
public async Task<Restaurants.Restaurant?> GetRestaurant(string name) { using var db = new RestaurantsContext(ConnectionString); var dbRestaurant = await db.Restaurants.FirstOrDefaultAsync(r => r.Name == name); if (dbRestaurant == null) return null; return ToDomainModel(dbRestaurant); }
The method now queries the database, and EF automatically returns a populated object. This would be nice if it was the right kind of object, but alas, it isn't. GetRestaurant still has to call a helper method to convert to the correct Domain Object:
private static Restaurants.Restaurant ToDomainModel(Restaurant restaurant) { return new Restaurants.Restaurant( restaurant.Id, restaurant.Name, new MaitreD( new TimeOfDay(restaurant.OpensAt), new TimeOfDay(restaurant.LastSeating), restaurant.SeatingDuration, restaurant.Tables.Select(ToDomainModel).ToList())); }
While this helper method converts an EF Restaurant object to a proper Domain Object (Restaurants.Restaurant), it also needs another helper to convert the table objects:
private static Restaurants.Table ToDomainModel(Table table) { if (table.IsCommunal) return Restaurants.Table.Communal(table.Capacity); else return Restaurants.Table.Standard(table.Capacity); }
As should be clear by now, using vanilla EF doesn't reduce the need for mapping.
Granted, the mapping code is a bit simpler, but you still need to remember to map restaurant.Name to the right constructor parameter, restaurant.OpensAt and restaurant.LastSeating to their correct places, table.Capacity to a constructor argument, and so on. If you make changes to the database schema or the Domain Model, you'll need to edit this code.
Encapsulation #
This is the point where more than one reader wonders: Can't you just..?
In short, no, I can't just.
The most common reaction is most likely that I'm doing this all wrong. I'm supposed to use the EF classes as my Domain Model.
But I can't, and I won't. I can't because I already have classes in place that serve that purpose. I also will not, because it would violate the Dependency Inversion Principle. As I recently described, the architecture is Ports and Adapters, or, if you will, Clean Architecture. The database Adapter should depend on the Domain Model; the Domain Model shouldn't depend on the database implementation.
Okay, but couldn't I have generated the EF classes in the Domain Model? After all, a class like the above Table is just a POCO Entity. It doesn't depend on the Entity Framework. I could have those classes in my Domain Model, put my DbContext in the data access layer, and have the best of both worlds. Right?
The code shown so far hints at a particular API afforded by the Domain Model. If you've read my book, you already know what comes next. Here's the Table Domain Model's API:
public sealed class Table { public static Table Standard(int seats) public static Table Communal(int seats) public int Capacity { get; } public int RemainingSeats { get; } public Table Reserve(Reservation reservation) public T Accept<T>(ITableVisitor<T> visitor) }
A couple of qualities of this design should be striking: There's no visible constructor - not even one that takes parameters. Instead, the type affords two static creation functions. One creates a standard table, the other a communal table. My book describes the difference between these types, and so does the Maître d' kata.
This isn't some frivolous design choice of mine, but rather quite deliberate. That Table class is a Visitor-encoded sum type. You can debate whether I should have modelled a table as a sum type or a polymorphic object, but now that I've chosen a sum type, it should be explicit in the API design.
"Explicit is better than implicit."
When we program, we make many mistakes. It's important to discover the mistakes as soon as possible. With a compiled language, the first feedback you get is from the compiler. I favour leveraging the compiler, and its type system, to prevent as many mistakes as possible. That's what Hillel Wayne calls constructive data. Make illegal states unrepresentable.
I could, had I thought of it at the time, have introduced a predicative natural-number wrapper of integers, in which case I could have strengthened the contract of Table even further:
public sealed class Table { public static Table Standard(NaturalNumber capacity) public static Table Communal(NaturalNumber capacity) public NaturalNumber Capacity { get; } public int RemainingSeats { get; } public Table Reserve(Reservation reservation) public T Accept<T>(ITableVisitor<T> visitor) }
The point is that I take encapsulation seriously, and my interpretation of the concept is heavily inspired by Bertrand Meyer's Object-Oriented Software Construction. The view of encapsulation emphasises contracts (preconditions, invariants, postconditions) rather than information hiding.
As I described in a previous article, you can't model all preconditions and invariants with types, but you can still let the type system do much heavy lifting.
This principle applies to all classes that are part of the Domain Model; not only Table, but also Restaurant:
public sealed class Restaurant { public Restaurant(int id, string name, MaitreD maitreD) public int Id { get; } public string Name { get; } public MaitreD MaitreD { get; } public Restaurant WithId(int newId) public Restaurant WithName(string newName) public Restaurant WithMaitreD(MaitreD newMaitreD) public Restaurant Select(Func<MaitreD, MaitreD> selector) }
While this class does have a public constructor, it makes use of another design choice that Entity Framework doesn't support: It nests one rich object (MaitreD) inside another. Why does it do that?
Again, this is far from a frivolous design choice I made just to be difficult. Rather, it's a result of a need-to-know principle (which strikes me as closely related to the Single Responsibility Principle): A class should only contain the information it needs in order to perform its job.
The MaitreD class does all the heavy lifting when it comes to deciding whether or not to accept reservations, how to allocate tables, etc. It doesn't, however, need to know the id or name of the restaurant in order to do that. Keeping that information out of MaitreD, and instead in the Restaurant wrapper, makes the code simpler and easier to use.
The bottom line of all this is that I value encapsulation over 'easy' database mapping.
Limitations of Entity Framework #
The promise of an object-relational mapper is that it automates mapping between objects and database. Is that promise realised?
In its current incarnation, it doesn't look as though Entity Framework supports mapping to and from the Domain Model. With the above tweaks, it supports the database schema that I've described, but only via 'Entity classes'. I still have to map to and from the 'Entity objects' and the actual Domain Model. Not much is gained.
One should, of course, be careful not drawing too strong inferences from this example. First, proving anything impossible is generally difficult. Just because I can't find a way to do what I want, I can't conclude that it's impossible. That a few other people tell me, too, that it's impossible still doesn't constitute strong evidence.
Second, even if it's impossible today, it doesn't follow that it will be impossible forever. Perhaps Entity Framework will support my Domain Model in the future.
Third, we can't conclude that just because Entity Framework (currently) doesn't support my Domain Model it follows that no object-relational mapper (ORM) does. There might be another ORM out there that perfectly supports my design, but I'm just not aware of it.
Based on my experience and what I see, read, and hear, I don't think any of that likely. Things might change, though.
Net benefit or drawback? #
Perhaps, despite all of this, you still prefer ORMs. You may compare my ADO.NET code to my Entity Framework code and conclude that the EF code still looks simpler. After all, when using ADO.NET I have to jump through some hoops to load the correct tables associated with each restaurant, whereas EF automatically handles that for me. The EF version requires fewer lines of code.
In isolation, the fewer lines of code the better. This seems like an argument for using an ORM after all, even if the original promise remains elusive. Take what you can get.
On the other hand, when you take on a dependency, there's usually a cost that comes along. A library like Entity Framework isn't free. While you don't pay a licence fee for it, it comes with other costs. You have to learn how to use it, and so do your colleagues. You also have to keep up to date with changes.
Every time some exotic requirement comes up, you'll have to spend time investigating how to address it with that ORM's API. This may lead to a game of Whac-A-Mole where every tweak to the ORM leads you further down the rabbit hole, and couples your code tighter with it.
You can only keep up with so many things. What's the best investment of your time, and the time of your team mates? Learning and knowing SQL, or learning and keeping up to date with a particular ORM?
I learned SQL decades ago, and that knowledge is still useful. On the other hand, I don't even know how many library and framework APIs that I've both learned and forgotten about.
As things currently stand, it looks to me as though the net benefit of using a library like Entity Framework is negative. Yes, it might save me a few lines of code, but I'm not ready to pay the costs just outlined.
This balance could tip in the future, or my context may change.
Conclusion #
For the kind of applications that I tend to become involved with, I don't find object-relational mappers particularly useful. When you have a rich Domain Model where the first design priority is encapsulation, assisted by the type system, it looks as though mapping is unavoidable.
While you can ask automated tools to generate code that mirrors a database schema (or the other way around), only classes with poor encapsulation are supported. As soon as you do something out of the ordinary like static factory methods or nested objects, apparently Entity Framework gives up.
Can we extrapolate from Entity Framework to other ORMs? Can we infer that Entity Framework will never be able to support objects with proper encapsulation, just because it currently doesn't?
I can't say, but I'd be surprised if things change soon, if at all. If, on the other hand, it eventually turns out that I can have my cake and eat it too, then why shouldn't I?
Until then, however, I don't find that the benefits of ORMs trump the costs of using them.
Comments
One project I worked on was (among other things) mapping data from database to rich domain objects in the way similar to what is described in this article. These object knew how to do a lot of things but were dependant on related objects and so everything neded to be loaded in advance from the database in order to ensure correctness. So having a Order, OrderLine, Person, Address and City, all the rows needed to be loaded in advance, mapped to objects and references set to create the object graph to be able to, say, display shipping costs based on person's address.
The mapping step involved cumbersome manual coding and was error prone because it was easy to forget to load some list or set some reference. Reflecting on that experience, it seems to me that sacrificing a bit of purity wrt domain modelling and leaning on an ORM to lazily load the references would have been much more efficient and correct.
But I guess it all depends on the context..?
Thanks. I've been following recent posts, but I was too lazy to go through the whole PRing things to reply. Maybe that's a good thing, since it forces you to think how to reply, instead of throwing a bunch of words together quickly. Anyways, back to business.
I'm not trying to sell one way or the other, because I'm seriously conflicted with both. Since most people on the web tend to fall into ORM category (in .NET world at least), I was simply looking for other perspective, from someone more knowledgable than me.
The following is just my thinking out loud...
You've used DB-first approach and scaffolding classes from DB schema. With EF core, the usual thing to do, is the opposite. Write classes to scaffold DB schema. Now, this doesn't save us from writing those "relational properties", but it allows us to generate DB update scripts. So if you have a class like:
class SomeTable
{
public int Id;
public string Name;
}
and you add a field:
class SomeTable
{
public int Id;
public string Name;
public DateTime Birthday;
}
you can run
add-migration MyMigration // generate migration file
update-database // execute it
This gives you a nice way to track DB chages via Git, but it can also introduce conflicts. Two devs cannot edit the same class/table. You have to be really careful when making commits. Another painful thing to do this way is creating DB views and stored procedures. I've honestly never saw a good solution for it. Maybe trying to do these things is a futile effort in the first place.
The whole
readByNameSql = @"SELECT [Id], [Name], [OpensAt], [LastSeating], [SeatingDuration]...
is giving me heebie jeebies. It is easy to change some column name, and introduce a bug. It might be possible to do stuff with string interpolation, but at that point, I'm thinking about creating my own framework...
The most common reaction is most likely that I'm doing this all wrong. I'm supposed to use the EF classes as my Domain Model. - Mark SeemannOne of the first things that I was taught on my first job, was to never expose my domain model to the outside world. The domain model being EF Core classes... These days, I'm thinking quite the opposite. EF Core classes are DTOs for the database (with some boilerplate in order for framework to do it's magic). I also want to expose my domain model to the outside world. Why not? That's the contract after all. But the problem with this, is that it adds another layer of mapping. Since my domain model validation is done in class constructor, deserialization of requests becomes a problem. Ideally, it should sit in a static method. But in that case I have: jsonDto -> domainModel -> dbDto. The No-ORM approach also still requires me to map domainModel to command parameters manually. All of this is a tedious, and very error prone process. Especially if you have the case like vlad mentioned above.
Minor observation on your code. People rarely map things from DB data to domain models when using EF Core. This is a horrible thing to do. Anyone can run a script against a DB, and corrupt the data. It is something I intend to enforce in future projects, if possible. Thank you F# community.
I can't think of anything more to say at the moment. Thanks again for a fully-fledged-article reply :). I also recommend this video. I haven't had the time to try things he is talking about yet.
Vlad, qfilip, thank you for writing.
I think your comments warrant another article. I'll post an update here later.
Quick update from me again. I've been thinking and experimenting with several approaches to solve issues I've written about above. How idealized world works and where do we make compromises. Forgive me for the sample types, I couldn't think of anything else. Let's assume we have this table:
type Sheikh = {
// db entity data
Id: Guid
CreatedAt: DateTime
ModifiedAt: DateTime
Deleted: bool
// domain data
Name: string
Email: string // unique constraint here
// relational data
Wives: Wife list
Supercars: Supercar list
}
I've named first 3 fields as "entity data". Why would my domain model contain an ID? It shouldn't care about persistence. I may save it to the DB, write it to a text file, or print it on a piece of paper. Don't care. We put IDs because data usually ends up in a DB. I could have used Email here to serve as an ID, because it should be unique, but we also like to standardize these stuff. All IDs shall be uuids.
There are also these "CreatedAt", "ModifiedAt" and "Deleted" columns. This is something I usually do, when I want soft-delete functionality. Denoramalize the data to gain performance. Otherwise, I would need to make... say... EntityStatus table to keep that data, forcing me to do a JOIN for every read operation and additional UPDATE EntityStatus for every write operation. So I kinda sidestep "the good practices" to avoid very real complications.
Domain data part is what it is, so I can safely skip that part.
Relational data part is the most interesting bit. I think this is what keeps me falling back to EntityFramework and why using "relational properties" are unavoidable. Either that, or I'm missing something.
Focusing attention on Sheikh table here, with just 2 relations, there are 4 potential scenarios. I don't want to load stuff from the DB, unless they are required, so the scenarios are:
- Load
Sheikhwithout relational data - Load
SheikhwithWives - Load
SheikhwithSupercars - Load
SheikhwithWivesandSupercars
2NRelations I guess? I'm three beers in on this, with only six hours left until corporate clock starts ticking, so my math is probably off.
God forbid if any of these relations have their own "inner relations" you may or may not need to load. This is where the (magic mapping/to SQL translations) really start getting useful. There will be some code repetition, but you'll just need to add ThenInclude(x => ...) and you're done.
Now the flip side. Focusing attention on Supercar table:
type Supercar = {
// db entity data
...
// domain data
Vendor: string
Model: string
HorsePower: int
// relational data
Owner: Sheikh
OwnerId: Guid
}
Pretty much same as before. Sometimes I'll need Sheikh info, sometimes I won't. One of F# specific problems I'm having is that, records require all fields to be populated. What if I need just SheikhID to perform some domain logic?
let tuneSheikhCars (sheikhId) (hpIncrement) (cars) =
cars
|> List.filter (fun x -> x.Owner.Id = sheikhId)
|> List.map (fun x -> x with { HorsePower = x.HorsePower + hpIncrement })
Similar goes for inserting new Supercar. I want to query-check first if Owner/Sheikh exists, before attempting insertion. You can pass it as a separate parameter, but code gets messier and messier.
No matter how I twist and turn things around, in the real world, I'm not only concerned by current steps I need to take to complete a task, but also with possible future steps. Now, I could define a record that only contains relevant data per each request. But, as seen above, I'd be eventually forced to make ~ 2NRelations of such records, instead of one. A reusable one, that serves like a bucket for a preferred persistence mechanism, allowing me to load relations later on, because nothing lives in memory long term.
I strayed away slightly here from ORM vs no-ORM discussion that I've started earlier. Because, now I realize that this problem isn't just about mapping things from type A to type B.
ValidationResult as a return type, but now we're entering a territory where C#, as a language, is totally unprepared for.
Just my two cents:
Yes, it is possible to map the NaturalNumber object to an E.F class property using ValueConverters. Here are a couple of articles talking about this:
- Andrew Lock: Using strongly-typed entity IDs to avoid primitive obsession.
- Thomas Levesque: Using C# 9 records as strongly-typed ids.
But even though you can use this, you may still encounter another use cases that you cannot tackle. E.F is just a tool with its limitations, and there will be things you can do with simple C# that you can not do with E.F.
I think you need to consider why you want to use E.F, understand its strengths and weaknesses, and then decide if it suits your project.
Do you want to use EF solely as a data access layer, or do you want it to be your domain layer?. Maybe for a big project you can use only E.F as a data access layer and use old plain C# files for domain layer. In a [small | medium | quick & dirty] project use as your domain layer.
There are bad thing we already know:
- Increased complexity.
- There will be things you can not do. So you must be carefull you will not need something E.F can not give you.
- You need to know how it works. For example, know that accessing
myRestaurant.MaitreDimplies a new database access (if you have not loaded it previously).
But sometimes E.F shines, for example:
- You are programing against the E.F model, not against a specific database, so it is easier to migrate to another database.
- Maybe migrate to another database is rare, but it is very convenient to run tests against an in-memory SQLite database. Tests against a real database can be run in the CD/CI environment, for example.
- Having a centralized point to process changes (
SaveChanges) allows you to easily do interesting things: save "CreatedBy," "CreatedDate," "ModifiedBy," and "ModifiedDate" fields for all tables or create historical tables (if you do not have access to the SQL Server temporal tables). - Global query filters allow you to make your application multi-tenant with very little code: all tables implement
IByClient, a global filter for theses tables... and voilà, your application becomes multi-client with just a few lines.
I am not a E.F defender, in fact I have a love & hate reletaionship with it. But I believe it is a powerful tool for certain projects. As always, the important thing is to think whether it is the right tool for your specific project :)
Thank you, all, for writing. There's more content in your comments than I can address in one piece, but I've written a follow-up article that engages with some of your points: Domain Model first.
Specifically regarding the point of having to hand-write a lot of code to deal with multiple tables joined in various fashions, I grant that while typing isn't a bottleneck, the more code you add, the greater the risk of bugs. I'm not trying to be dismissive of ORMs as a general tool. If you truly, inescapably, have a relational model, then an ORM seems like a good choice. If so, however, I don't see that you can get good encapsulation at the same time.
And indeed, an important responsibility of a software architect is to consider trade-offs to find a good solution for a particular problem. Sometimes such a solution involves an ORM, but sometimes, it doesn't. In my world, it usually doesn't.
Do I breathe rarefied air, dealing with esoteric problems that mere mortals can never hope to encounter? I don't think so. Rather, I offer the interpretation that I sometimes approach problems in a different way. All I really try to do with these articles is to present to the public the ways I think about problems. I hope, then, that it may inspire other people to consider problems from more than one angle.
Finally, from my various customer engagements I get the impression that people also like ORMs because 'entity classes' look strongly typed. As a counter-argument, I suggest that this may be an illusion.

Comments
Heh, that's fair criticism, not finger pointing. I wanted to give a better example here, but I gave up halfway through writing it. You raised some good points. I'll have to rethink my approach on domain modeling further, before asking any meaningful questions.
Years of working with EF-Core in a specific way got me... indoctrinated. Not all things are bad ofcourse, but I have missed the bigger picture in some areas, as far as I can tell.
Thanks for dedicating so many articles to the subject.