ploeh blog danish software design
Test-driving the pyramid's top
Some thoughts on TDD related to integration and systems testing.
My recent article Works on most machines elicited some responses. Upon reflection, it seems that most of the responses relate to the top of the Test Pyramid.
While I don't have an one-shot solution that addresses all concerns, I hope that nonetheless I can suggest some ideas and hopefully inspire a reader or two. That's all. I intend nothing of the following to be prescriptive. I describe my own professional experience: What has worked for me. Perhaps it could also work for you. Use the ideas if they inspire you. Ignore them if you find them impractical.
The Test Pyramid #
The Test Pyramid is often depicted like this:
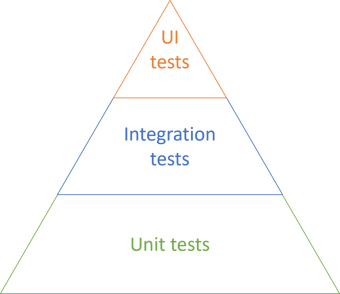
This seems to indicate that while the majority of tests should be unit tests, you should also have a substantial number of integration tests, and quite a few UI tests.
Perhaps the following is obvious, but the Test Pyramid is an idea; it's a way to communicate a concept in a compelling way. What one should take away from it, I think, is only this: The number of tests in each category should form a total order, where the unit test category is the maximum. In other words, you should have more unit tests than you have tests in the next category, and so on.
No-one says that you can only have three levels, or that they have to have the same height. Finally, the above figure isn't even a pyramid, but rather a triangle.
I sometimes think of the Test Pyramid like this:
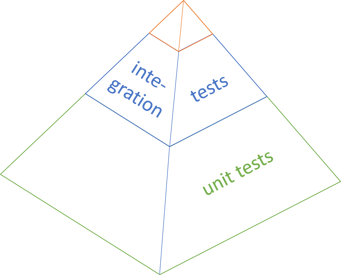
To be honest, it's not so much whether or not the pyramid is shown in perspective, but rather that the unit test base is significantly more voluminous than the other levels, and that the top is quite small.
Levels #
In order to keep the above discussion as recognisable as possible, I've used the labels unit tests, integration tests, and UI tests. It's easy to get caught up in a discussion about how these terms are defined. Exactly what is a unit test? How does it differ from an integration test?
There's no universally accepted definition of a unit test, so it tends to be counter-productive to spend too much time debating the finer points of what to call the tests in each layer.
Instead, I find the following criteria useful:
- In-process tests
- Tests that involve more than one process
- Tests that can only be performed in production
I'll describe each in a little more detail. Along the way, I'll address some of the reactions to Works on most machines.
In-process tests #
The in-process category corresponds roughly to the Test Pyramid's unit test level. It includes 'traditional' unit tests such as tests of stand-alone functions or methods on objects, but also Facade Tests. The latter may involve multiple modules or objects, perhaps even from multiple libraries. Many people may call them integration tests because they integrate more than one module.
As long as an automated test runs in a single process, in memory, it tends to be fast and leave no persistent state behind. This is almost exclusively the kind of test I tend to test-drive. I often follow an outside-in TDD process, an example of which is shown in my book Code That Fits in Your Head.
Consider an example from the source code that accompanies the book:
[Fact] public async Task ReserveTableAtTheVaticanCellar() { using var api = new SelfHostedApi(); var client = api.CreateClient(); var timeOfDayLaterThanLastSeatingAtTheOtherRestaurants = TimeSpan.FromHours(21.5); var at = DateTime.Today.AddDays(433).Add( timeOfDayLaterThanLastSeatingAtTheOtherRestaurants); var dto = Some.Reservation.WithDate(at).ToDto(); var response = await client.PostReservation("The Vatican Cellar", dto); response.EnsureSuccessStatusCode(); }
I think of a test like this as an automated acceptance test. It uses an internal test-specific domain-specific language (test utilities) to exercise the REST service's API. It uses ASP.NET self-hosting to run both the service and the HTTP client in the same process.
Even though this may, at first glance, look like an integration test, it's an artefact of test-driven development. Since it does cut across both HTTP layer and domain model, some readers may think of it as an integration test. It uses a stateful in-memory data store, so it doesn't involve more than a single process.
Tests that span processes #
There are aspects of software that you can't easily drive with tests. I'll return to some really gnarly examples in the third category, but in between, we find concerns that are hard, but still possible to test. The reason that they are hard is often because they involve more than one process.
The most common example is data access. Many software systems save or retrieve data. With test-driven development, you're supposed to let the tests inform your API design decisions in such a way that everything that involves difficult, error-prone code is factored out of the data access layer, and into another part of the code that can be tested in process. This development technique ought to drain the hard-to-test components of logic, leaving behind a Humble Object.
One reaction to Works on most machines concerns exactly that idea:
"As a developer, you need to test HumbleObject's behavior."
It's almost tautologically part of the definition of a Humble Object that you're not supposed to test it. Still, realistically, ladeak has a point.
When I wrote the example code to Code That Fits in Your Head, I applied the Humble Object pattern to the data access component. For a good while, I had a SqlReservationsRepository class that was so simple, so drained of logic, that it couldn't possibly fail.
Until, of course, the inevitable happened: There was a bug in the SqlReservationsRepository code. Not to make a long story out of it, but even with a really low cyclomatic complexity, I'd accidentally swapped two database columns when reading from a table.
Whenever possible, when I discover a bug, I first write an automated test that exposes that bug, and only then do I fix the problem. This is congruent with my lean bias. If a defect can occur once, it can occur again in the future, so it's better to have a regression test.
The problem with this bug is that it was in a Humble Object. So, ladeak is right. Sooner or later, you'll have to test the Humble Object, too.
That's when I had to bite the bullet and add a test library that tests against the database.
One such test looks like this:
[Theory] [InlineData(Grandfather.Id, "2022-06-29 12:00", "e@example.gov", "Enigma", 1)] [InlineData(Grandfather.Id, "2022-07-27 11:40", "c@example.com", "Carlie", 2)] [InlineData(2, "2021-09-03 14:32", "bon@example.edu", "Jovi", 4)] public async Task CreateAndReadRoundTrip( int restaurantId, string at, string email, string name, int quantity) { var expected = new Reservation( Guid.NewGuid(), DateTime.Parse(at, CultureInfo.InvariantCulture), new Email(email), new Name(name), quantity); var connectionString = ConnectionStrings.Reservations; var sut = new SqlReservationsRepository(connectionString); await sut.Create(restaurantId, expected); var actual = await sut.ReadReservation(restaurantId, expected.Id); Assert.Equal(expected, actual); }
The entire test runs in a special context where a database is automatically created before the test runs, and torn down once the test has completed.
"When building such behavior, you can test against a shared instance of the service in your dev team or run that service on your dev machine in a container."
Yes, those are two options. A third, in the spirit of GOOS, is to strongly favour technologies that support automation. Believe it or not, you can automate SQL Server. You don't need a Docker container for it. That's what I did in the above test.
I can see how a Docker container with an external dependency can be useful too, so I'm not trying to dismiss that technology. The point is, however, that simpler alternatives may exist. I, and others, did test-driven development for more than a decade before Docker existed.
Tests that can only be performed in production #
The last category of tests are those that you can only perform on a production system. What might be examples of that?
I've run into a few over the years. One such test is what I call a Smoke Test: Metaphorically speaking, turn it on and see if it develops smoke. These kinds of tests are good at catching configuration errors. Does the web server have the right connection string to the database? A test can verify whether that's the case, but it makes no sense to run such a test on a development machine, or against a test system, or a staging environment. You want to verify that the production system is correctly configured. Only a test against the production system can do that.
For every configuration value, you may want to consider a Smoke Test.
There are other kinds of tests you can only perform in production. Sometimes, it's not technical concerns, but rather legal or financial constraints, that dictate circumstances.
A few years ago I worked with a software organisation that, among other things, integrated with the Danish personal identification number system (CPR). Things may have changed since, but back then, an organisation had to have a legal agreement with CPR before being granted access to its integration services. It's an old system (originally from 1968) with a proprietary data integration protocol.
We test-drove a parser of the data format, but that still left behind a Humble Object that would actually perform the data transfers. How do we test that Humble Object?
Back then, at least, there was no test system for the CPR service, and it was illegal to query the live system unless you had a business reason. And software testing did not constitute a legal reason.
The only legal option was to make the Humble Object as simple and foolproof as possible, and then observe how it worked in actual production situations. Containers wouldn't help in such a situation.
It's possible to write automated tests against production systems, but unless you're careful, they're difficult to write and maintain. At least, go easy on the assertions, since you can't assume much about the run-time data and behaviour of a live system. Smoke tests are mostly just 'pings', so can be written to be fairly maintenance-free, but you shouldn't need many of them.
Other kinds of tests against production are likely to be fragile, so it pays to minimise their number. That's the top of the pyramid.
User interfaces #
I no longer develop user interfaces, so take the following with a pinch of salt.
The 'original' Test Pyramid that I've depicted above has UI tests at the pyramid's top. That doesn't necessarily match the categories I've outlined here; don't assume parity.
A UI test may or may not involve more than one process, but they are often difficult to maintain for other reasons. Perhaps this is where the pyramid metaphor starts to break down. All models are wrong, but some are useful.
Back when I still programmed user interfaces, I'd usually test-drive them via a subcutaneous API, and rely on some variation of MVC to keep the rendered controls in sync. Still, once in a while, you need to verify that the user interface looks as it's supposed to. Often, the best tool for that job is the good old Mark I Eyeball.
This still means that you need to run the application from time to time.
"Docker is also very useful for enabling others to run your software on their machines. Recently, we've been exploring some apps that consisted of ~4 services (web servers) and a database. All of them written in different technologies (PHP, Java, C#). You don't have to setup environment variables. You don't need to have relevant SDKs to build projects etc. Just run docker command, and spin them instantly on your PC."
That sounds like a reasonable use case. I've never found myself in such circumstances, but I can imagine the utility that containers offer in a situation like that. Here's how I envision the scenario:
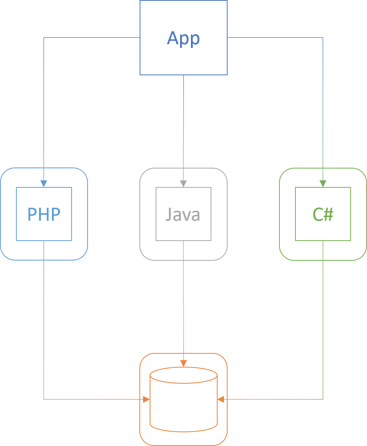
The boxes with rounded corners symbolise containers.
Again, my original goal with the previous article wasn't to convince you that container technologies are unequivocally bad. Rather, it was to suggest that test-driven development (TDD) solves many of the problems that people seem to think can only be solved with containers. Since TDD has many other beneficial side effects, it's worth considering instead of mindlessly reaching for containers, which may represent only a local maximum.
How could TDD address qfilip's concern?
When I test-drive software, I favour real dependencies, and I favour Fake objects over Mocks and Stubs. Were I to return to user-interface programming today, I'd define its external dependencies as one or more interfaces, and implement a Fake Object for each.
Not only will this enable me to simulate the external dependencies with the Fakes. If I implement the Fakes as part of the production code, I'd even be able to spin up the system, using the Fakes instead of the real system.

A Fake is an implementation that 'almost works'. A common example is an in-memory collection instead of a database. It's neither persistent nor thread-safe, but it's internally consistent. What you add, you can retrieve, until you delete it again. For the purposes of starting the app in order to verify that the user interface looks correct, that should be good enough.
Another related example is NServiceBus, which comes with a file transport that is clearly labeled as not for production use. While it's called the Learning Transport, it's also useful for exploratory testing on a development machine. While this example clearly makes use of an external resource (the file system), it illustrates how a Fake implementation can alleviate the need for a container.
Uses for containers #
Ultimately, it's still useful to be able to stand up an entire system, as qfilip suggests, and if containers is a good way to do that, it doesn't bother me. At the risk of sounding like a broken record, I never intended to say that containers are useless.
When I worked as a Software Development Engineer in Microsoft, I had two computers: A laptop and a rather beefy tower PC. I've always done all programming on laptops, so I repurposed the tower as a virtual server with all my system's components on separate virtual machines (VM). The database in one VM, the application server in another, and so on. I no longer remember what all the components were, but I seem to recall that I had four VMs running on that one box.
While I didn't use it much, I found it valuable to occasionally verify that all components could talk to each other on a realistic network topology. This was in 2008, and Docker wasn't around then, but I could imagine it would have made that task easier.
I don't dispute that Docker and Kubernetes are useful, but the job of a software architect is to carefully identify the technologies on which a system should be based. The more technology dependencies you take on, the more rigid the design.
After a few decades of programming, my experience is that as a programmer and architect, I can find better alternatives than depending on container technologies. If testers and IT operators find containers useful to do their jobs, then that's fine by me. Since my code works on most machines, it works in containers, too.
Truly Humble Objects #
One last response, and I'll wrap this up.
"As a developer, you need to test HumbleObject's behavior. What if a DatabaseConnection or a TCP conn to a message queue is down?"
How should such situations be handled? There may always be special cases, but in general, I can think of two reactions:
- Log the error
- Retry the operation
Assuming that the Humble Object is a polymorphic type (i.e. inherits a base class or implements an interface), you should be able to extract each of these behaviours to general-purpose components.
In order to log errors, you can either use a Decorator or a global exception handler. Most frameworks provide a way to catch (otherwise) unhandled exceptions, exactly for this purpose, so you don't have to add such functionality to a Humble Object.
Retry logic can also be delegated to a third-party component. For .NET I'd start looking at Polly, but I'd be surprised if other platforms don't have similar libraries that implement the stability patterns from Release It.
Something more specialised, like a fail-over mechanism, sounds like a good reason to wheel out the Chain of Responsibility pattern.
All of these can be tested independently of any Humble Object.
Conclusion #
In a recent article I reflected on my experience with TDD and speculated that a side effect of that process is code flexible enough to work on most machines. Thus, I've never encountered the need for a containers.
Readers responded with comments that struck me as mostly related to the upper levels of the Test Pyramid. In this article, I've attempted to address some of those concerns. I still get by without containers.
Is software getting worse?
A rant, with some examples.
I've been a software user for thirty years.
My first PC was DOS-based. In my first job, I used OS/2, in the next, Windows 3.11, NT, and later incarnations of Windows.
I wrote my first web sites in Arachnophilia, and my first professional software in Visual Basic, Visual C++, and Visual InterDev.
I used Terminate with my first modem. If I recall correctly, it had a built-in email downloader and offline reader. Later, I switched to Outlook for email. I've used Netscape Navigator, Internet Explorer, Firefox, and Chrome to surf the web.
I've written theses, articles, reports, etc. in Word Perfect for DOS and MS Word for Windows. I wrote my new book Code That Fits In your Head in TexStudio. Yes, it was written entirely in LaTeX.
Updates #
For the first fifteen years, new software version were rare. You'd get a version of AutoCAD, Windows, or Visual C++, and you'd use it for years. After a few years, a new version would come out, and that would be a big deal.
Interim service releases were rare, too, since there was no network-based delivery mechanism. Software came on floppy disks, and later on CDs.
Even if a bug fix was easy to make, it was difficult for a software vendor to distribute it, so most software releases were well-tested. Granted, software had bugs back then, and some of them you learned to work around.
When a new version came out, the same forces were at work. The new version had to be as solid and stable as the previous one. Again, I grant that once in a while, even in those days, this wasn't always the case. Usually, a bad release spelled the demise of a company, because release times were so long that competitors could take advantage of a bad software release.
Usually, however, software updates were improvements, and you looked forward to them.
Decay #
I no longer look forward to updates. These days, software is delivered over the internet, and some applications update automatically.
From a security perspective it can be a good idea to stay up-to-date, and for years, I diligently did that. Lately, however, I've become more conservative. Particularly when it comes to Windows, I ignore all suggestions to update it until it literally forces the update on me.
Just like even-numbered Star Trek movies don't suck the same pattern seems to be true for Windows: Windows XP was good, Windows 7 was good, and Windows 10 wasn't bad either. I kept putting off Windows 11 for as long as possible, but now I use it, and I can't say that I'm surprised that I don't like it.
This article, however, isn't a rant about Windows in particular. This seems to be a general trend, and it's been noticeable for years.
Examples #
I think that the first time I noticed a particular application degrading was Vivino. It started out as a local company here in Copenhagen, and I was a fairly early adopter. Initially, it was great: If you like wine, but don't know that much about it, you could photograph a bottle's label, and it'd automatically recognise the wine and register it in your 'wine library'. I found it useful that I could look up my notes about a wine I'd had a year ago to remind me what I thought of it. As time went on, however, I started to notice errors in my wine library. It might be double entries, or wines that were silently changed to another vintage, etc. Eventually it got so bad that I lost trust in the application and uninstalled it.
Another example is Sublime Text, which I used for writing articles for this blog. I even bought a licence for it. Version 3 was great, but version 4 was weird from the outset. One thing was that they changed how they indicated which parts of a file I'd edited after opening it, and I never understood the idea behind the visuals. Worse was that auto-closing of HTML stopped working. Since I'm that weird dude who writes raw HTML, such a feature is quite important to me. If I write an HTML tag, I expect the editor to automatically add the closing tag, and place my cursor between the two. Sublime Text stopped doing that consistently, and eventually it became annoying enough that I though: Why bother? Now I write in Visual Studio Code.
Microsoft is almost a chapter in itself, but to be fair, I don't consider Microsoft products worse than others. There's just so much of it, and since I've always been working in the Microsoft tech stack, I use a lot of it. Thus, selection bias clearly is at work here. Still, while I don't think Microsoft is worse than the competition, it seems to be part of the trend.
For years, my login screen was stuck on the same mountain lake, even though I tried every remedy suggested on the internet. Eventually, however, a new version of Windows fixed the issue. So, granted, sometimes new versions improve things.
Now, however, I have another problem with Windows Spotlight. It shows nice pictures, and there used to be an option to see where the picture was taken. Since I repaved my machine, this option is gone. Again, I've scoured the internet for resolutions to this problem, but neither rebooting, regedit changes, etc. has so far solved the problem.
That sounds like small problems, so let's consider something more serious. Half a year ago, Outlook used to be able to detect whether I was writing an email in English or Danish. It could even handle the hybrid scenario where parts of an email was in English, and parts in Danish. Since I repaved my machine, this feature no longer works. Outlook doesn't recognise Danish when I write it. One thing are the red squiggly lines under most words, but that's not even the worst. The worst part of this is that even though I'm writing in Danish, outlook thinks I'm writing in English, so it silently auto-corrects Danish words to whatever looks adjacent in English.
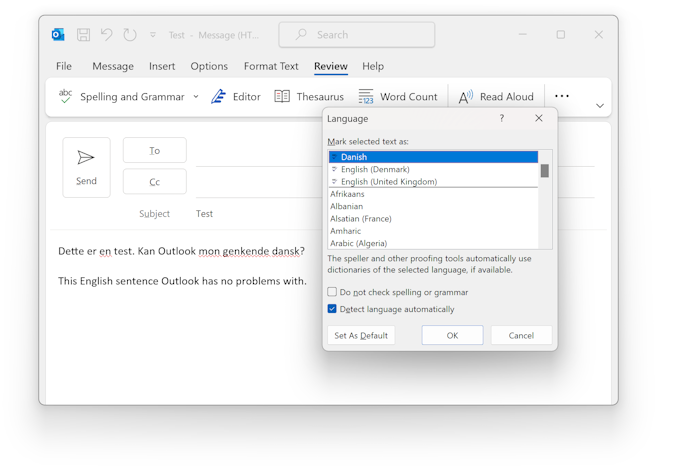
This became so annoying that I contacted Microsoft support about it, but while they had me try a number of things, nothing worked. They eventually had to give up and suggested that I reinstalled my machine - which, at that point, I'd done two weeks before.
This used to work, but now it doesn't.
It's not all bad #
I could go on with other examples, but I think that this suffices. After all, I don't think it makes for a compelling read.
Of course, not everything is bad. While it looks as though I'm particularly harping on Microsoft, I rarely detect problems with Visual Studio or Code, and I usually install updates as soon as they are available. The same is true for much other software I use. Paint.NET is awesome, MusicBee is solid, and even the Sonos Windows app, while horrific, is at least consistently so.
Conclusion #
It seems to me that some software is actually getting worse, and that this is a more recent trend.
The point isn't that some software is bad. This has always been the case. What seems new to me is that software that used to be good deteriorates. While this wasn't entirely unheard of in the nineties (I'm looking at you, WordPerfect), this is becoming much more noticeable.
Perhaps it's just frequency illusion, or perhaps it's because I use software much more than I did in the nineties. Still, I can't shake the feeling that some software is deteriorating.
Why does this happen? I don't know, but my own bias suggests that it's because there's less focus on regression testing. Many of the problems I see look like regression bugs to me. A good engineering team could have caught them with automated regression tests, but these days, it seems as though many teams rely on releasing often and then letting users do the testing.
The problem with that approach, however, is that if you don't have good automated tests, fixing one regression may resurrect another.
Works on most machines
TDD encourages deployment flexibility. Functional programming also helps.
Recently several of the podcasts I subscribe to have had episodes about various container technologies, of which Kubernetes dominates. I tune out of such content, since it has nothing to do with me.
I've never found containerisation relevant. I remember being fascinated when I first heard of Docker, and for a while, I awaited a reason to use it. It never materialised.
I'd test-drive whatever system I was working on, and deploy it to production. Usually, it'd just work.
Since my process already produced good results, why make it more complicated?
Occasionally, I would become briefly aware of the lack of containers in my life, but then I'd forget about it again. Until now, I haven't thought much about it, and it's probably only the random coincidence of a few podcast episodes back-to-back that made me think more about it.
Be liberal with what system you run on #
When I was a beginner programmer a few years ago, things were different. I'd write code that worked on my machine, but not always on the test server.
As I gained experience, this tended to happen less often. This doubtlessly have multiple causes, and increased experience is likely one of them, but I also think that my interest in loose coupling and test-driven development plays a role.
Increasingly I developed an ethos of writing software that would work on most machines, instead of only my own. It seems reminiscent of Postel's law: Be liberal with what system you run on.
Test-driven development helps in that regard, because you write code that must be able to execute in at least two contexts: The test context, and the actual system context. These two contexts both exist on your machine.
A colleague once taught me: The most difficult generalisation step is going from one to two. Once you've generalised to two cases, it's much easier to generalise to three, four, or n cases.
It seems to me that such from-one-to-two-cases generalisation is an inadvertent by-product of test-driven development. Once your code already matches two different contexts, making it even more flexible isn't that much extra work. It's not even speculative generality because you also need to make it work on the production system and (one hopes) on a build server or continuous delivery pipeline. That's 3-4 contexts. Odds are that software that runs successfully in four separate contexts runs successfully on many more systems.
General-purpose modules #
In A Philosophy of Software Design John Ousterhout argues that one should aim for designing general-purpose objects or modules, rather than specialised APIs. He calls them deep modules and their counterparts shallow modules. On the surface, this seems to go against the grain of YAGNI, but the way I understand the book, the point is rather that general-purpose solutions also solve special cases, and, when done right, the code doesn't have to be more complicated than the one that handles the special case.
As I write in my review of the book, I think that there's a connection with test-driven development. General-purpose code is code that works in more than one situation, including automated testing environments. This is almost tautological. If it doesn't work in an automated test, an argument could be made that it's insufficiently general.
Likewise, general-purpose software should be able to work when deployed to more than one machine. It should even work on machines where other versions of that software already exist.
When you have general-purpose software, though, do you really need containers?
Isolation #
While I've routinely made use of test-driven development since 2003, I started my shift towards functional programming around ten years later. I think that this has amplified my code's flexibility.
As Jessica Kerr pointed out years ago, a corollary of referential transparency is that pure functions are isolated from their environment. Only input arguments affect the output of a pure function.
Ultimately, you may need to query the environment about various things, but in functional programming, querying the environment is impure, so you push it to the boundary of the system. Functional programming encourages you to explicitly consider and separate impure actions from pure functions. This implies that the environment-specific code is small, cohesive, and easy to review.
Conclusion #
For a while, when Docker was new, I expected it to be a technology that I'd eventually pick up and make part of my tool belt. As the years went by, that never happened. As a programmer, I've never had the need.
I think that a major contributor to that is that since I mostly develop software with test-driven development, the resulting software is already robust or flexible enough to run in multiple environments. Adding functional programming to the mix helps to achieve isolation from the run-time environment.
All of this seems to collaborate to enable code to work not just on my machine, but on most machines. Including containers.
Perhaps there are other reasons to use containers and Kubernetes. In a devops context, I could imagine that it makes deployment and operations easier. I don't know much about that, but I also don't mind. If someone wants to take the code I've written and run it in a container, that's fine. It's going to run there too.
Comments
Commenting for the first time. I hope I made these changes in proper manner. Anyway...
Kubernetes usually also means the usage of cloud infrastructure, and as such, it can be automated (and change-tracked) in various interesting ways. Is it worth it? Well, that depends as always... Docker isn't the only container technology supported by k8s, but since it's the most popular one... they go hand in hand.
Docker is also very useful for enabling others to run your software on their machines. Recently, we've been exploring some apps that consisted of ~4 services (web servers) and a database. All of them written in different technologies (PHP, Java, C#). You don't have to setup environment variables. You don't need to have relevant SDKs to build projects etc. Just run docker command, and spin them instantly on your PC.
So there's that...
Unrelated to the topic above, I'd like to ask you, if you could write an article on the specific subject. Or, if the answer is short, comment me back. As an F# enthusiast, I find yours and Scott's blog very valuable. One thing I've failed to find here is why you don't like ORMs. I think the words were they solve a problem that we shouldn't have in the first place. Since F# doesn't play too well with Entity Framework, and I pretty much can't live without it... I'm curious if I'm missing something. A different approach, way of thinking. I can work with raw SQL ofcourse... but the mapping... oh the mapping...
I'm contemplating turning my response into a new article, but it may take some time before I get to it. I'll post here once I have a more thorough response.
qfilip, thank you for writing. I've now published the article that, among many other things, respond to your comment about containers.
I'll get back to your question about ORMs as soon as possible.
I'm still considering how to best address the question about ORMs, but in the meanwhile, I'd like to point interested readers to Ted Neward's famous article The Vietnam of Computer Science.
Finally, I'm happy to announce that I've written an article trying to explain my position: Do ORMs reduce the need for mapping?.
AI for doc comments
A solution in search of a problem?
I was recently listening to a podcast episode where the guest (among other things) enthused about how advances in large language models mean that you can now get these systems to write XML doc comments.
You know, these things:
/// <summary> /// Scorbles a dybliad. /// </summary> /// <param name="dybliad">The dybliad to scorble.</param> /// <param name="flag"> /// A flag that controls wether scorbling is done pre- or postvotraid. /// </param> /// <returns>The scorbled dybliad.</returns> public string Scorble(string dybliad, bool flag)
And it struck me how that's not the first time I've encountered that notion. Finally, you no longer need to write those tedious documentation comments in your code. Instead, you can get Github Copilot or ChatGPT to write them for you.
When was the last time you wrote such comments?
I'm sure that there are readers who wrote some just yesterday, but generally, I rarely encounter them in the wild.
As a rule, I only write them when my modelling skills fail me so badly that I need to apologise in code. Whenever I run into such a situation, I may as well take advantage of the format already in place for such things, but it's not taking up a big chunk of my time.
It's been a decade since I ran into a code base where doc comments were mandatory. When I had to write comments, I'd use GhostDoc, which used heuristics to produce 'documentation' on par with modern AI tools.
Whether you use GhostDoc, Github Copilot, or write the comments yourself, most of them tend to be equally inane and vacuous. Good design only amplifies this quality. The better names you use, and the more you leverage the type system to make illegal states unrepresentable, the less you need the kind of documentation furnished by doc comments.
I find it striking that more than one person wax poetic about AI's ability to produce doc comments.
Is that, ultimately, the only thing we'll entrust to large language models?
I know that that they can do more than that, but are we going to let them? Or is automatic doc comments a solution in search of a problem?
Validating or verifying emails
On separating preconditions from business rules.
My recent article Validation and business rules elicited this question:
"Regarding validation should be pure function, lets have user registration as an example, is checking the email address uniqueness a validation or a business rule? It may not be pure since the check involves persistence mechanism."
This is a great opportunity to examine some heuristics in greater detail. As always, this mostly presents how I think about problems like this, and so doesn't represent any rigid universal truth.
The specific question is easily answered, but when the topic is email addresses and validation, I foresee several follow-up questions that I also find interesting.
Uniqueness constraint #
A new user signs up for a system, and as part of the registration process, you want to verify that the email address is unique. Is that validation or a business rule?
Again, I'm going to put the cart before the horse and first use the definition to answer the question.
Validation is a pure function that decides whether data is acceptable.
Can you implement the uniqueness constraint with a pure function? Not easily. What most systems would do, I'm assuming, is to keep track of users in some sort of data store. This means that in order to check whether or not a email address is unique, you'd have to query that database.
Querying a database is non-deterministic because you could be making multiple subsequent queries with the same input, yet receive differing responses. In this particular example, imagine that you ask the database whether ann.siebel@example.com is already registered, and the answer is no, that address is new to us.
Database queries are snapshots in time. All that answer tells you is that at the time of the query, the address would be unique in your database. While that answer travels over the network back to your code, a concurrent process might add that very address to the database. Thus, the next time you ask the same question: Is ann.siebel@example.com already registered? the answer would be: Yes, we already know of that address.
Verifying that the address is unique (most likely) involves an impure action, and so according to the above definition isn't a validation step. By the law of the the excluded middle, then, it must be a business rule.
Using a different rule of thumb, Robert C. Martin arrives at the same conclusion:
"Uniqueness is semantic not syntactic, so I vote that uniqueness is a business rule not a validation rule."
This highlights a point about this kind of analysis. Using functional purity is a heuristic shortcut to sorting verification problems. Those that are deterministic and have no side effects are validation problems, and those that are either non-deterministic or have side effects are not.
Being able to sort problems in this way is useful because it enables you to choose the right tool for the job, and to avoid the wrong tool. In this case, trying to address the uniqueness constraint with validation is likely to cause trouble.
Why is that? Because of what I already described. A database query is a snapshot in time. If you make a decision based on that snapshot, it may be the wrong decision once you reach a conclusion. Granted, when discussing user registration, the risk of several processes concurrently trying to register the same email address probably isn't that big, but in other domains, contention may be a substantial problem.
Being able to identify a uniqueness constraint as something that isn't validation enables you to avoid that kind of attempted solution. Instead, you may contemplate other designs. If you keep users in a relational database, the easiest solution is to put a uniqueness constraint on the Email column and let the database deal with the problem. Just be prepared to handle the exception that the INSERT statement may generate.
If you have another kind of data store, there are other ways to model the constraint. You can even do so using lock-free architectures, but that's out of scope for this article.
Validation checks preconditions #
Encapsulation is an important part of object-oriented programming (and functional programming as well). As I've often outlined, I base my understanding of encapsulation on Object-Oriented Software Construction. I consider contract (preconditions, invariants, and postconditions) essential to encapsulation.
I'll borrow a figure from my article Can types replace validation?:

The role of validation is to answer the question: Does the data make sense?
This question, and its answer, is typically context-dependent. What 'makes sense' means may differ. This is even true for email addresses.
When I wrote the example code for my book Code That Fits in Your Head, I had to contemplate how to model email addresses. Here's an excerpt from the book:
Email addresses are notoriously difficult to validate, and even if you had a full implementation of the SMTP specification, what good would it do you?
Users can easily give you a bogus email address that fits the spec. The only way to really validate an email address is to send a message to it and see if that provokes a response (such as the user clicking on a validation link). That would be a long-running asynchronous process, so even if you'd want to do that, you can't do it as a blocking method call.
The bottom line is that it makes little sense to validate the email address, apart from checking that it isn't null. For that reason, I'm not going to validate it more than I've already done.
In this example, I decided that the only precondition I would need to demand was that the email address isn't null. This was motivated by the operations I needed to perform with the email address - or rather, in this case, the operations I didn't need to perform. The only thing I needed to do with the address was to save it in a database and send emails:
public async Task EmailReservationCreated(int restaurantId, Reservation reservation) { if (reservation is null) throw new ArgumentNullException(nameof(reservation)); var r = await RestaurantDatabase.GetRestaurant(restaurantId).ConfigureAwait(false); var subject = $"Your reservation for {r?.Name}."; var body = CreateBodyForCreated(reservation); var email = reservation.Email.ToString(); await Send(subject, body, email).ConfigureAwait(false); }
This code example suggests why I made it a precondition that Email mustn't be null. Had null be allowed, I would have had to resort to defensive coding, which is exactly what encapsulation makes redundant.
Validation is a process that determines whether data is useful in a particular context. In this particular case, all it takes is to check the Email property on the DTO. The sample code that comes with Code That Fits in Your Head shows the basics, while An applicative reservation validation example in C# contains a more advanced solution.
Preconditions are context-dependent #
I would assume that a normal user registration process has little need to validate an ostensible email address. A system may want to verify the address, but that's a completely different problem. It usually involves sending an email to the address in question and have some asynchronous process register if the user verifies that email. For an article related to this problem, see Refactoring registration flow to functional architecture.
Perhaps you've been reading this with mounting frustration: How about validating the address according to the SMTP spec?
Indeed, that sounds like something one should do, but turns out to be rarely necessary. As already outlined, users can easily supply a bogus address like foo@bar.com. It's valid according to the spec, and so what? How does that information help you?
In most contexts I've found myself, validating according to the SMTP specification is a distraction. One might, however, imagine scenarios where it might be required. If, for example, you need to sort addresses according to user name or host name, or perform some filtering on those parts, etc. it might be warranted to actually require that the address is valid.
This would imply a validation step that attempts to parse the address. Once again, parsing here implies translating less-structured data (a string) to more-structured data. On .NET, I'd consider using the MailAddress class which already comes with built-in parser functions.
The point being that your needs determine your preconditions, which again determine what validation should do. The preconditions are context-dependent, and so is validation.
Conclusion #
Email addresses offer a welcome opportunity to discuss the difference between validation and verification in a way that is specific, but still, I hope, easy to extrapolate from.
Validation is a translation from one (less-structured) data format to another. Typically, the more-structured data format is an object, a record, or a hash map (depending on language). Thus, validation is determined by two forces: What the input data looks like, and what the desired object requires; that is, its preconditions.
Validation is always a translation with the potential for error. Some input, being less-structured, can't be represented by the more-structured format. In addition to parsing, a validation function must also be able to fail in a composable matter. That is, fortunately, a solved problem.
Validation and business rules
A definition of validation as distinguished from business rules.
This article suggests a definition of validation in software development. A definition, not the definition. It presents how I currently distinguish between validation and business rules. I find the distinction useful, although perhaps it's a case of reversed causality. The following definition of validation is useful because, if defined like that, it's a solved problem.
My definition is this:
Validation is a pure function that decides whether data is acceptable.
I've used the word acceptable because it suggests a link to Postel's law. When validating, you may want to allow for some flexibility in input, even if, strictly speaking, it's not entirely on spec.
That's not, however, the key ingredient in my definition. The key is that validation should be a pure function.
While this may sound like an arbitrary requirement, there's a method to my madness.
Business rules #
Before I explain the benefits of the above definition, I think it'll be useful to outline typical problems that developers face. My thesis in Code That Fits in Your Head is that understanding limits of human cognition is a major factor in making a code base sustainable. This again explains why encapsulation is such an important idea. You want to confine knowledge in small containers that fit in your head. Information shouldn't leak out of these containers, because that would require you to keep track of too much stuff when you try to understand other code.
When discussing encapsulation, I emphasise contract over information hiding. A contract, in the spirit of Object-Oriented Software Construction, is a set of preconditions, invariants, and postconditions. Preconditions are particularly relevant to the topic of validation, but I've often experienced that some developers struggle to identify where validation ends and business rules begin.
Consider an online restaurant reservation system as an example. We'd like to implement a feature that enables users to make reservations. In order to meet that end, we decide to introduce a Reservation class. What are the preconditions for creating a valid instance of such a class?
When I go through such an exercise, people quickly identify requirement such as these:
- The reservation should have a date and time.
- The reservation should contain the number of guests.
- The reservation should contain the name or email (or other data) about the person making the reservation.
A common suggestion is that the restaurant should also be able to accommodate the reservation; that is, it shouldn't be fully booked, it should have an available table at the desired time of an appropriate size, etc.
That, however, isn't a precondition for creating a valid Reservation object. That's a business rule.
Preconditions are self-contained #
How do you distinguish between a precondition and a business rule? And what does that have to do with input validation?
Notice that in the above examples, the three preconditions I've listed are self-contained. They are statements about the object or value's constituent parts. On the other hand, the requirement that the restaurant should be able to accommodate the reservation deals with a wider context: The table layout of the restaurant, prior reservations, opening and closing times, and other business rules as well.
Validation is, as Alexis King points out, a parsing problem. You receive less-structured data (CSV, JSON, XML, etc.) and attempt to project it to a more-structured format (C# objects, F# records, Clojure maps, etc.). This succeeds when the input satisfies the preconditions, and fails otherwise.
Why can't we add more preconditions than required? Consider Postel's law. An operation (and that includes object constructors) should be liberal in what it accepts. While you have to draw the line somewhere (you can't really work with a reservation if the date is missing), an object shouldn't require more than it needs.
In general we observe that the fewer pre-conditions, the easier it is to create an object (or equivalent functional data structure). As a counter-example, this explains why Active Record is antithetical to unit testing. One precondition is that there's a database available, and while not impossible to automate in tests, it's quite the hassle. It's easier to work with POJOs in tests. And unit tests, being the first clients of an API, tell you how easy it is to use that API.
Contracts with third parties #
If validation is fundamentally parsing, it seems reasonable that operations should be pure functions. After all, a parser operates on unchanging (less-structured) data. A programming-language parser takes contents of text files as input. There's little need for more input than that, and the output is expected to be deterministic. Not surprisingly, Haskell is well-suited for writing parsers.
You don't, however, have to buy the argument that validation is essentially parsing, so consider another perspective.
Validation is a data transformation step you perform to deal with input. Data comes from a source external to your system. It can be a user filling in a form, another program making an HTTP request, or a batch job that receives files over FTP.
Even if you don't have a formal agreement with any third party, Hyrum's law implies that a contract does exist. It behoves you to pay attention to that, and make it as explicit as possible.
Such a contract should be stable. Third parties should be able to rely on deterministic behaviour. If they supply data one day, and you accept it, you can't reject the same data the next days on grounds that it was malformed. At best, you may be contravariant in input as time passes; in other words, you may accept things tomorrow that you didn't accept today, but you may not reject tomorrow what you accepted today.
Likewise, you can't have validation rules that erratically accept data one minute, reject the same data the next minute, only to accept it later. This implies that validation must, at least, be deterministic: The same input should always produce the same output.
That's half of the way to referential transparency. Do you need side effects in your validation logic? Hardly, so you might as well implement it as pure functions.
Putting the cart before the horse #
You may still think that my definition smells of a solution in search of a problem. Yes, pure functions are convenient, but does it naturally follow that validation should be implemented as pure functions? Isn't this a case of poor retconning?
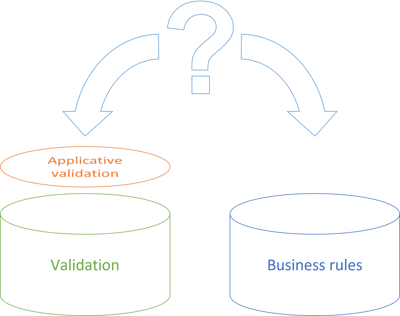
When faced with the question: What is validation, and what are business rules? it's almost as though I've conveniently sized the Validation sorting bucket so that it perfectly aligns with applicative validation. Then, the Business rules bucket fits whatever is left. (In the figure, the two buckets are of equal size, which hardly reflects reality. I estimate that the Business rules bucket is much larger, but had I tried to illustrate that, too, in the figure, it would have looked akilter.)
This is suspiciously convenient, but consider this: My experience is that this perspective on validation works well. To a great degree, this is because I consider validation a solved problem. It's productive to be able to take a chunk of a larger problem and put it aside: We know how to deal with this. There are no risks there.
Definitions do, I believe, rarely spring fully formed from some Platonic ideal. Rather, people observe what works and eventually extract a condensed description and call it a definition. That's what I've attempted to do here.
Business rules change #
Let's return to the perspective of validation as a technical contract between your system and a third party. While that contract should be as stable as possible, business rules change.
Consider the online restaurant reservation example. Imagine that you're the third-party programmer, and that you've developed a client that can make reservations on behalf of users. When a user wants to make a reservation, there's always a risk that it's not possible. Your client should be able to handle that scenario.
Now the restaurant becomes so popular that it decides to change a rule. Earlier, you could make reservations for one, three, or five people, even though the restaurant only has tables for two, four, or six people. Based on its new-found popularity, the restaurant decides that it only accepts reservations for entire tables. Unless it's on the same day and they still have a free table.
This changes the behaviour of the system, but not the contract. A reservation for three is still valid, but will be declined because of the new rule.
"Things that change at the same rate belong together. Things that change at different rates belong apart."
Business rules change at different rates than preconditions, so it makes sense to decouple those concerns.
Conclusion #
Since validation is a solved problem, it's useful to be able to identify what is validation, and what is something else. As long as an 'input rule' is self-contained (or parametrisable), deterministic, and has no side-effects, you can model it with applicative validation.
Equally useful is it to be able to spot when applicative validation isn't a good fit. While I'm sure that someone has published a ValidationT monad transformer for Haskell, I'm not sure I would recommend going that route. In other words, if some business operation involves impure actions, it's not going to fit the mold of applicative validation.
This doesn't mean that you can't implement business rules with pure functions. You can, but in my experience, abstractions other than applicative validation are more useful in those cases.
When is an implementation detail an implementation detail?
On the tension between encapsulation and testability.
This article is part of a series called Epistemology of interaction testing. A previous article in the series elicited this question:
"following your suggestion, aren’t we testing implementation details?"
This frequently-asked question reminds me of an old joke. I think that I first heard it in the eighties, a time when phones had rotary dials, everyone smoked, you'd receive mail through your apartment door's letter slot, and unemployment was high. It goes like this:
A painter gets a helper from the unemployment office. A few days later the lady from the office calls the painter and apologizes deeply for the mistake.
"What mistake?"
"I'm so sorry, instead of a painter we sent you a gynaecologist. Please just let him go, we'll send you a..."
"Let him go? Are you nuts, he's my best worker! At the last job, they forgot to leave us the keys, and the guy painted the whole room through the letter slot!"
I always think of this joke when the topic is testability. Should you test everything through a system's public API, or do you choose to expose some internal APIs in order to make the code more testable?
Letter slots #
Consider the simplest kind of program you could write: Hello world. If you didn't consider automated testing, then an idiomatic C# implementation might look like this:
internal class Program { private static void Main(string[] args) { Console.WriteLine("Hello, World!"); } }
(Yes, I know that with modern C# you can write such a program using a single top-level statement, but I'm writing for a broader audience, and only use C# as an example language.)
How do we test a program like that? Of course, no-one seriously suggests that we really need to test something that simple, but what if we make it a little more complex? What if we make it possible to supply a name as a command-line argument? What if we want to internationalise the program? What if we want to add a help feature? What if we want to add a feature so that we can send a hello to another recipient, on another machine? When does the behaviour become sufficiently complex to warrant automated testing, and how do we achieve that goal?
For now, I wish to focus on how to achieve the goal of testing software. For the sake of argument, then, assume that we want to test the above hello world program.
As given, we can run the program and verify that it prints Hello, World! to the console. This is easy to do as a manual test, but harder if you want to automate it.
You could write a test framework that automatically starts a new operating-system process (the program) and waits until it exits. This framework should be able to handle processes that exit with success and failure status codes, as well as processes that hang, or never start, or keep restarting... Such a framework also requires a way to capture the standard output stream in order to verify that the expected text is written to it.
I'm sure such frameworks exist for various operating systems and programming languages. There is, however, a simpler solution if you can live with the trade-off: You could open the API of your source code a bit:
public class Program { public static void Main(string[] args) { Console.WriteLine("Hello, World!"); } }
While I haven't changed the structure or the layout of the source code, I've made both class and method public. This means that I can now write a normal C# unit test that calls Program.Main.
I still need a way to observe the behaviour of the program, but there are known ways of redirecting the Console output in .NET (and I'd be surprised if that wasn't the case on other platforms and programming languages).
As we add more and more features to the command-line program, we may be able to keep testing by calling Program.Main and asserting against the redirected Console. As the complexity of the program grows, however, this starts to look like painting a room through the letter slot.
Adding new APIs #
Real programs are usually more than just a command-line utility. They may be smartphone apps that react to user input or network events, or web services that respond to HTTP requests, or complex asynchronous systems that react to, and send messages over durable queues. Even good old batch jobs are likely to pull data from files in order to write to a database, or the other way around. Thus, the interface to the rest of the world is likely larger than just a single Main method.
Smartphone apps or message-based systems have event handlers. Web sites or services have classes, methods, or functions that handle incoming HTTP requests. These are essentially event handlers, too. This increases the size of the 'test surface': There are more than a single method you can invoke in order to exercise the system.
Even so, a real program will soon grow to a size where testing entirely through the real-world-facing API becomes reminiscent of painting through a letter slot. J.B. Rainsberger explains that one major problem is the combinatorial explosion of required test cases.
Another problem is that the system may produce side effects that you care about. As a basic example, consider a system that, as part of its operation, sends emails. When testing this system, you want to verify that under certain circumstances, the system sends certain emails. How do you do that?
If the system has absolutely no concessions to testability, I can think of two options:
- You contact the person to whom the system sends the email, and ask him or her to verify receipt of the email. You do that every time you test.
- You deploy the System Under Test in an environment with an SMTP gateway that redirects all email to another address.
Clearly the first option is unrealistic. The second option is a little better, but you still have to open an email inbox and look for the expected message. Doing so programmatically is, again, technically possible, and I'm sure that there are POP3 or IMAP assertion libraries out there. Still, this seems complicated, error-prone, and slow.
What could we do instead? I would usually introduce a polymorphic interface such as IPostOffice as a way to substitute the real SmtpPostOffice with a Test Double.
Notice what happens in these cases: We introduce (or make public) new APIs in order to facilitate automated testing.
Application-boundary API and internal APIs #
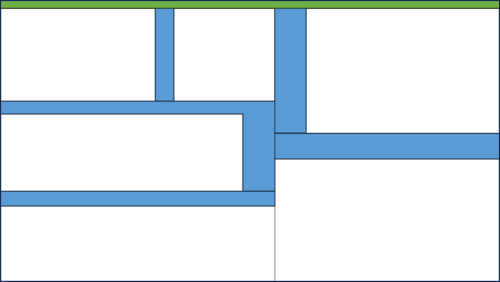
It's helpful to distinguish between the real-world-facing API and everything else. In this diagram, I've indicated the public-facing API as a thin green slice facing upwards (assuming that external stimulus - button clicks, HTTP requests, etc. - arrives from above).
The real-world-facing API is the code that must be present for the software to work. It could be a button-click handler or an ASP.NET action method:
[HttpPost("restaurants/{restaurantId}/reservations")] public async Task<ActionResult> Post(int restaurantId, ReservationDto dto)
Of course, if you're using another web framework or another programming language, the details differ, but the application has to have code that handles an HTTP POST request on matching addresses. Or a button click, or a message that arrives on a message bus. You get the point.
These APIs are fairly fixed. If you change them, you change the externally observable behaviour of the system. Such changes are likely breaking changes.
Based on which framework and programming language you're using, the shape of these APIs will be given. Like I did with the above Main method, you can make it public and use it for testing.
A software system of even middling complexity will usually also be decomposed into smaller components. In the figure, I've indicated such subdivisions as boxes with gray outlines. Each of these may present an API to other parts of the system. I've indicated these APIs with light blue.
The total size of internal APIs is likely to be larger than the public-facing API. On the other hand, you can (theoretically) change these internal interfaces without breaking the observable behaviour of the system. This is called refactoring.
These internal APIs will often have public access modifiers. That doesn't make them real-world-facing. Be careful not to confuse programming-language access modifiers with architectural concerns. Objects or their members can have public access modifiers even if the object plays an exclusively internal role. At the boundaries, applications aren't object-oriented. And neither are they functional.
Likewise, as the original Main method example shows, public APIs may be implemented with a private access modifier.
Why do such internal APIs exist? Is it only to support automated testing?
Decomposition #
If we introduce new code, such as the above IPostOffice interface, in order to facilitate testing, we have to be careful that it doesn't lead to test-induced design damage. The idea that one might introduce an API exclusively to support automated testing rubs some people the wrong way.
On the other hand, we do introduce (or make public) APIs for other reasons, too. One common reason is that we want to decompose an application's source code so that parallel development is possible. One person (or team) works on one part, and other people work on other parts. If those parts need to communicate, we need to agree on a contract.
Such a contract exists for purely internal reasons. End users don't care, and never know of it. You can change it without impacting users, but you may need to coordinate with other teams.
What remains, though, is that we do decompose systems into internal parts, and we've done this since before Parnas wrote On the Criteria to Be Used in Decomposing Systems into Modules.
Successful test-driven development introduces seams where they ought to be in any case.
Testing implementation details #
An internal seam is an implementation detail. Even so, when designed with care, it can serve multiple purposes. It enables teams to develop in parallel, and it enables automated testing.
Consider the example from a previous article in this series. I'll repeat one of the tests here:
[Theory] [AutoData] public void HappyPath(string state, string code, (string, bool, Uri) knownState, string response) { _repository.Add(state, knownState); _stateValidator .Setup(validator => validator.Validate(code, knownState)) .Returns(true); _renderer .Setup(renderer => renderer.Success(knownState)) .Returns(response); _target .Complete(state, code) .Should().Be(response); }
This test exercises a happy-path case by manipulating IStateValidator and IRenderer Test Doubles. It's a common approach to testability, and what dhh would label test-induced design damage. While I'm sympathetic to that position, that's not my point. My point is that I consider IStateValidator and IRenderer internal APIs. End users (who probably don't even know what C# is) don't care about these interfaces.
Tests like these test against implementation details.
This need not be a problem. If you've designed good, stable seams then these tests can serve you for a long time. Testing against implementation details become a problem if those details change. Since it's hard to predict how things change in the future, it behoves us to decouple tests from implementation details as much as possible.
The alternative, however, is mail-slot testing, which comes with its own set of problems. Thus, judicious introduction of seams is helpful, even if it couples tests to implementation details.
Actually, in the question I quoted above, Christer van der Meeren asked whether my proposed alternative isn't testing implementation details. And, yes, that style of testing also relies on implementation details for testing. It's just a different way to design seams. Instead of designing seams around polymorphic objects, we design them around pure functions and immutable data.
There are, I think, advantages to functional programming, but when it comes to relying on implementation details, it's only on par with object-oriented design. Not worse, not better, but the same.
Conclusion #
Every API in use carries a cost. You need to keep the API stable so that users can use it tomorrow like they did yesterday. This can make it difficult to evolve or improve an API, because you risk introducing a breaking change.
There are APIs that a system must have. Software exists to be used, and whether that entails a user clicking on a button or another computer system sending a message to your system, your code must handle such stimulus. This is your real-world-facing contract, and you need to be careful to keep it consistent. The smaller that surface area is, the simpler that task is.
The same line of reasoning applies to internal APIs. While end users aren't impacted by changes in internal seams, other code is. If you change an implementation detail, this could cost maintenance work somewhere else. (Modern IDEs can handle some changes like that automatically, such as method renames. In those cases, the cost of change is low.) Therefore, it pays to minimise the internal seams as much as possible. One way to do this is by decoupling to delete code.
Still, some internal APIs are warranted. They help you decompose a large system into smaller subparts. While there's a potential maintenance cost with every internal API, there's also the advantage of working with smaller, independent units of code. Often, the benefits are larger than the cost.
When done well, such internal seams are useful testing APIs as well. They're still implementation details, though.
Collatz sequences by function composition
Mostly in C#, with a few lines of Haskell code.
A recent article elicited more comments than usual, and I've been so unusually buried in work that only now do I have a little time to respond to some of them. In one comment Struan Judd offers a refactored version of my Collatz sequence in order to shed light on the relationship between cyclomatic complexity and test case coverage.
Struan Judd's agenda is different from what I have in mind in this article, but the comment inspired me to refactor my own code. I wanted to see what it would look like with this constraint: It should be possible to test odd input numbers without exercising the code branches related to even numbers.
The problem with more naive implementations of Collatz sequence generators is that (apart from when the input is 1) the sequence ends with a tail of even numbers halving down to 1. I'll start with a simple example to show what I mean.
Standard recursion #
At first I thought that my confusion originated from the imperative structure of the original example. For more than a decade, I've preferred functional programming (FP), and even when I write object-oriented code, I tend to use concepts and patterns from FP. Thus I, naively, rewrote my Collatz generator as a recursive function:
public static IReadOnlyCollection<int> Sequence(int n) { if (n < 1) throw new ArgumentOutOfRangeException( nameof(n), $"Only natural numbers allowed, but given {n}."); if (n == 1) return new[] { n }; else if (n % 2 == 0) return new[] { n }.Concat(Sequence(n / 2)).ToArray(); else return new[] { n }.Concat(Sequence(n * 3 + 1)).ToArray(); }
Recursion is usually not recommended in C#, because a sufficiently long sequence could blow the call stack. I wouldn't write production C# code like this, but you could do something like this in F# or Haskell where the languages offer solutions to that problem. In other words, the above example is only for educational purposes.
It doesn't, however, solve the problem that confused me: If you want to test the branch that deals with odd numbers, you can't avoid also exercising the branch that deals with even numbers.
Calculating the next value #
In functional programming, you solve most problems by decomposing them into smaller problems and then compose the smaller Lego bricks with standard combinators. It seemed like a natural refactoring step to first pull the calculation of the next value into an independent function:
public static int Next(int n) { if ((n % 2) == 0) return n / 2; else return n * 3 + 1; }
This function has a cyclomatic complexity of 2 and no loops or recursion. Test cases that exercise the even branch never touch the odd branch, and vice versa.
A parametrised test might look like this:
[Theory] [InlineData( 2, 1)] [InlineData( 3, 10)] [InlineData( 4, 2)] [InlineData( 5, 16)] [InlineData( 6, 3)] [InlineData( 7, 22)] [InlineData( 8, 4)] [InlineData( 9, 28)] [InlineData(10, 5)] public void NextExamples(int n, int expected) { int actual = Collatz.Next(n); Assert.Equal(expected, actual); }
The NextExamples test obviously defines more than the two test cases that are required to cover the Next function, but since code coverage shouldn't be used as a target measure, I felt that more than two test cases were warranted. This often happens, and should be considered normal.
A Haskell proof of concept #
While I had a general idea about the direction in which I wanted to go, I felt that I lacked some standard functional building blocks in C#: Most notably an infinite, lazy sequence generator. Before moving on with the C# code, I threw together a proof of concept in Haskell.
The next function is just a one-liner (if you ignore the optional type declaration):
next :: Integral a => a -> a next n = if even n then n `div` 2 else n * 3 + 1
A few examples in GHCi suggest that it works as intended:
ghci> next 2 1 ghci> next 3 10 ghci> next 4 2 ghci> next 5 16
Haskell comes with enough built-in functions that that was all I needed to implement a Colaltz-sequence generator:
collatz :: Integral a => a -> [a] collatz n = (takeWhile (1 <) $ iterate next n) ++ [1]
Again, a few examples suggest that it works as intended:
ghci> collatz 1 [1] ghci> collatz 2 [2,1] ghci> collatz 3 [3,10,5,16,8,4,2,1] ghci> collatz 4 [4,2,1] ghci> collatz 5 [5,16,8,4,2,1]
I should point out, for good measure, that since this is a proof of concept I didn't add a Guard Clause against zero or negative numbers. I'll keep that in the C# code.
Generator #
While C# does come with a TakeWhile function, there's no direct equivalent to Haskell's iterate function. It's not difficult to implement, though:
public static IEnumerable<T> Iterate<T>(Func<T, T> f, T x) { var current = x; while (true) { yield return current; current = f(current); } }
While this Iterate implementation has a cyclomatic complexity of only 2, it exhibits the same kind of problem as the previous attempts at a Collatz-sequence generator: You can't test one branch without testing the other. Here, it even seems as though it's impossible to test the branch that skips the loop.
In Haskell the iterate function is simply a lazily-evaluated recursive function, but that's not going to solve the problem in the C# case. On the other hand, it helps to know that the yield keyword in C# is just syntactic sugar over a compiler-generated Iterator.
Just for the exercise, then, I decided to write an explicit Iterator instead.
Iterator #
For the sole purpose of demonstrating that it's possible to refactor the code so that branches are independent of each other, I rewrote the Iterate function to return an explicit IEnumerable<T>:
public static IEnumerable<T> Iterate<T>(Func<T, T> f, T x) { return new Iterable<T>(f, x); }
The Iterable<T> class is a private helper class, and only exists to return an IEnumerator<T>:
private sealed class Iterable<T> : IEnumerable<T> { private readonly Func<T, T> f; private readonly T x; public Iterable(Func<T, T> f, T x) { this.f = f; this.x = x; } public IEnumerator<T> GetEnumerator() { return new Iterator<T>(f, x); } IEnumerator IEnumerable.GetEnumerator() { return GetEnumerator(); } }
The Iterator<T> class does the heavy lifting:
private sealed class Iterator<T> : IEnumerator<T> { private readonly Func<T, T> f; private readonly T original; private bool iterating; internal Iterator(Func<T, T> f, T x) { this.f = f; original = x; Current = x; } public T Current { get; private set; } [MaybeNull] object IEnumerator.Current => Current; public void Dispose() { } public bool MoveNext() { if (iterating) Current = f(Current); else iterating = true; return true; } public void Reset() { Current = original; iterating = false; } }
I can't think of a situation where I would write code like this in a real production code base. Again, I want to stress that this is only an exploration of what's possible. What this does show is that all members have low cyclomatic complexity, and none of them involve looping or recursion. Only one method, MoveNext, has a cyclomatic complexity greater than one, and its branches are independent.
Composition #
All Lego bricks are now in place, enabling me to compose the Sequence like this:
public static IReadOnlyCollection<int> Sequence(int n) { if (n < 1) throw new ArgumentOutOfRangeException( nameof(n), $"Only natural numbers allowed, but given {n}."); return Generator.Iterate(Next, n).TakeWhile(i => 1 < i).Append(1).ToList(); }
This function has a cyclomatic complexity of 2, and each branch can be exercised independently of the other.
Which is what I wanted to accomplish.
Conclusion #
I'm still re-orienting myself when it comes to understanding the relationship between cyclomatic complexity and test coverage. As part of that work, I wanted to refactor the Collatz code I originally showed. This article shows one way to decompose and reassemble the function in such a way that all branches are independent of each other, so that each can be covered by test cases without exercising the other branch.
I don't know if this is useful to anyone else, but I found the hours well-spent.
Comments
I really like this article. So much so that I tried to implement this approach for a recursive function at my work. However, I realized that there are some required conditions.
First, the recusrive funciton must be tail recursive. Second, the recursive function must be closed (i.e. the output is a subset/subtype of the input). Neither of those were true for my function at work. An example of a function that doesn't satisfy either of these conditions is the function that computes the depth of a tree.
A less serious issue is that your code, as currently implemented, requires that there only be one base case value. The issue is that you have duplicated code: the unique base case value appears both in the call to TakeWhile and in the subsequent call to Append. Instead of repeating yourself, I recommend defining an extension method on Enumerable called TakeUntil that works like TakeWhile but also returns the first value on which the predicate returned false. Here is an implementation of that extension method.
Tyson, thank you for writing. I suppose that you can't share the function that you mention, so I'll have to discuss it in general terms.
As far as I can tell you can always(?) refactor non-tail-recursive functions to tail-recursive implementations. In practice, however, there's rarely need for that, since you can usually separate the problem into a general-purpose library function on the one hand, and your special function on the other. Examples of general-purpose functions are the various maps and folds. If none of the standard functions do the trick, the type's associated catamorphism ought to.
One example of that is computing the depth of a tree, which we've already discussed.
I don't insist that any of this is universally true, so if you have another counter-example, I'd be keen to see it.
You are, of course, right about using a TakeUntil extension instead. I was, however, trying to use as many built-in components as possible, so as to not unduly confuse casual readers.
The Git repository that vanished
A pair of simple operations resurrected it.
The other day I had an 'interesting' experience. I was about to create a small pull request, so I checked out a new branch in Git and switched to my editor in order to start coding when the battery on my laptop died.
Clearly, when this happens, the computer immediately stops, without any graceful shutdown.
I plugged in the laptop and booted it. When I navigated to the source code folder I was working on, the files where there, but it was no longer a Git repository!
Git is fixable #
Git is more complex, and more powerful, than most developers care to deal with. Over the years, I've observed hundreds of people interact with Git in various ways, and most tend to give up at the first sign of trouble.
The point of this article isn't to point fingers at anyone, but rather to serve as a gentle reminder that Git tends to be eminently fixable.
Often, when people run into problems with Git, their only recourse is to delete the repository and clone it again. I've seen people do that enough times to realise that it might be helpful to point out: You may not have to do that.
Corruption #
Since I use Git tactically I have many repositories on my machine that have no remotes. In those cases, deleting the entire directory and cloning it from the remote isn't an option. I do take backups, though.
Still, in this story, the repository I was working with did have a remote. Even so, I was reluctant to delete everything and start over, since I had multiple branches and stashes I'd used for various experiments. Many of those I'd never pushed to the remote, so starting over would mean that I'd lose all of that. It was, perhaps, not a catastrophe, but I would certainly prefer to restore my local repository, if possible.
The symptoms were these: When you work with Git in Git Bash, the prompt will indicate which branch you're on. That information was absent, so I was already worried. A quick query confirmed my fears:
$ git status fatal: not a git repository (or any of the parent directories): .git
All the source code was there, but it looked as though the Git repository was gone. The code still compiled, but there was no source history.
Since all code files were there, I had hope. It helps knowing that Git, too, is file-based, and all files are in a hidden directory called .git. If all the source code was still there, perhaps the .git files were there, too. Why wouldn't they be?
$ ls .git COMMIT_EDITMSG description gitk.cache hooks/ info/ modules/ objects/ packed-refs config FETCH_HEAD HEAD index logs/ ms-persist.xml ORIG_HEAD refs/
Jolly good! The .git files were still there.
I now had a hypothesis: The unexpected shutdown of my machine had left some 'dangling pointers' in .git. A modern operating system may delay writes to disk, so perhaps my git checkout command had never made it all the way to disk - or, at least, not all of it.
If the repository was 'merely' corrupted in the sense that a few of the reference pointers had gone missing, perhaps it was fixable.
Empty-headed #
A few web searches indicated that the problem might be with the HEAD file, so I investigated its contents:
$ cat .git/HEAD
That was all. No output. The HEAD file was empty.
That file is not supposed to be empty. It's supposed to contain a commit ID or a reference that tells the Git CLI what the current head is - that is, which commit is currently checked out.
While I had checked out a new branch when my computer shut down, I hadn't written any code yet. Thus, the easiest remedy would be to restore the head to master. So I opened the HEAD file in Vim and added this to it:
ref: refs/heads/master
And just like that, the entire Git repository returned!
Bad object #
The branches, the history, everything looked as though it was restored. A little more investigation, however, revealed one more problem:
$ git log --oneline --all fatal: bad object refs/heads/some-branch
While a normal git log command worked fine, as soon as I added the --all switch, I got that bad object error message, with the name of the branch I had just created before the computer shut down. (The name of that branch wasn't some-branch - that's just a surrogate I'm using for this article.)
Perhaps this was the same kind of problem, so I explored the .git directory further and soon discovered a some-branch file in .git/refs/heads/. What did the contents look like?
$ cat .git/refs/heads/some-branch
Another empty file!
Since I had never committed any work to that branch, the easiest fix was to simply delete the file:
$ rm .git/refs/heads/some-branch
That solved that problem as well. No more fatal: bad object error when using the --all switch with git log.
No more problems have shown up since then.
Conclusion #
My experience with Git is that it's so powerful that you can often run into trouble. On the other hand, it's also so powerful that you can also use it to extricate yourself from trouble. Learning how to do that will teach you how to use Git to your advantage.
The problem that I ran into here wasn't fixable with the Git CLI itself, but turned out to still be easily remedied. A Git guru like Enrico Campidoglio could most likely have solved my problems without even searching the web. The details of how to solve the problems were new to me, but it took me a few web searches and perhaps five-ten minutes to fix them.
The point of this article, then, isn't in the details. It's that it pays to do a little investigation when you run into problems with Git. I already knew that, but I thought that this little story was a good occasion to share that knowledge.
Favour flat code file folders
How code files are organised is hardly related to sustainability of code bases.
My recent article Folders versus namespaces prompted some reactions. A few kind people shared how they organise code bases, both on Twitter and in the comments. Most reactions, however, carry the (subliminal?) subtext that organising code in file folders is how things are done.
I'd like to challenge that notion.
As is usually my habit, I mostly do this to make you think. I don't insist that I'm universally right in all contexts, and that everyone else are wrong. I only write to suggest that alternatives exist.
The previous article wasn't a recommendation; it's was only an exploration of an idea. As I describe in Code That Fits in Your Head, I recommend flat folder structures. Put most code files in the same directory.
Finding files #
People usually dislike that advice. How can I find anything?!
Let's start with a counter-question: How can you find anything if you have a deep file hierarchy? Usually, if you've organised code files in subfolders of subfolders of folders, you typically start with a collapsed view of the tree.
Those of my readers who know a little about search algorithms will point out that a search tree is an efficient data structure for locating content. The assumption, however, is that you already know (or can easily construct) the path you should follow.
In a view like the above, most files are hidden in one of the collapsed folders. If you want to find, say, the Iso8601.cs file, where do you look for it? Which path through the tree do you take?
Unfair!, you protest. You don't know what the Iso8601.cs file does. Let me enlighten you: That file contains functions that render dates and times in ISO 8601 formats. These are used to transmit dates and times between systems in a platform-neutral way.
So where do you look for it?
It's probably not in the Controllers or DataAccess directories. Could it be in the Dtos folder? Rest? Models?
Unless your first guess is correct, you'll have to open more than one folder before you find what you're looking for. If each of these folders have subfolders of their own, that only exacerbates the problem.
If you're curious, some programmer (me) decided to put the Iso8601.cs file in the Dtos directory, and perhaps you already guessed that. That's not the point, though. The point is this: 'Organising' code files in folders is only efficient if you can unerringly predict the correct path through the tree. You'll have to get it right the first time, every time. If you don't, it's not the most efficient way.
Most modern code editors come with features that help you locate files. In Visual Studio, for example, you just hit Ctrl+, and type a bit of the file name: iso:
Then hit Enter to open the file. In Visual Studio Code, the corresponding keyboard shortcut is Ctrl+p, and I'd be highly surprised if other editors didn't have a similar feature.
To conclude, so far: Organising files in a folder hierarchy is at best on par with your editor's built-in search feature, but is likely to be less productive.
Navigating a code base #
What if you don't quite know the name of the file you're looking for? In such cases, the file system is even less helpful.
I've seen people work like this:
- Look at some code. Identify another code item they'd like to view. (Examples may include: Looking at a unit test and wanting to see the SUT, or looking at a class and wanting to see the base class.)
- Move focus to the editor's folder view (in Visual Studio called the Solution Explorer).
- Scroll to find the file in question.
- Double-click said file.
Regardless of how the files are organised, you could, instead, go to definition (F12 with my Visual Studio keyboard layout) in a single action. Granted, how well this works varies with editor and language. Still, even when editor support is less optimal (e.g. a code base with a mix of F# and C#, or a Haskell code base), I can often find things faster with a search (Ctrl+Shift+f) than via the file system.
A modern editor has efficient tools that can help you find what you're looking for. Looking through the file system is often the least efficient way to find the code you're looking for.
Large code bases #
Do I recommend that you dump thousands of code files in a single directory, then?
Hardly, but a question like that presupposes that code bases have thousands of code files. Or more, even. And I've seen such code bases.
Likewise, it's a common complaint that Visual Studio is slow when opening solutions with hundreds of projects. And the day Microsoft fixes that problem, people are going to complain that it's slow when opening a solution with thousands of projects.
Again, there's an underlying assumption: That a 'real' code base must be so big.
Consider alternatives: Could you decompose the code base into multiple smaller code bases? Could you extract subsystems of the code base and package them as reusable packages? Yes, you can do all those things.
Usually, I'd pull code bases apart long before they hit a thousand files. Extract modules, libraries, utilities, etc. and put them in separate code bases. Use existing package managers to distribute these smaller pieces of code. Keep the code bases small, and you don't need to organise the files.
Maintenance #
But, if all files are mixed together in a single folder, how do we keep the code maintainable?
Once more, implicit (but false) assumptions underlie such questions. The assumption is that 'neatly' organising files in hierarchies somehow makes the code easier to maintain. Really, though, it's more akin to a teenager who 'cleans' his room by sweeping everything off the floor only to throw it into his cupboard. It does enable hoovering the floor, but it doesn't make it easier to find anything. The benefit is mostly superficial.
Still, consider a tree.
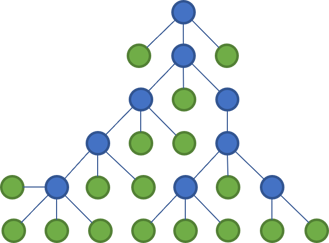
This may not be the way you're used to see files and folders rendered, but this diagram emphases the tree structure and makes what happens next starker.
The way that most languages work, putting code files in folders makes little difference to the compiler. If the classes in my Controllers folder need some classes from the Dtos folder, you just use them. You may need to import the corresponding namespace, but modern editors make that a breeze.
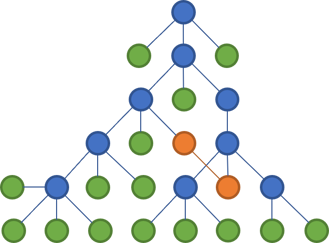
In the above tree, the two files who now communicate are coloured orange. Notice that they span across two main branches of the tree.
Thus, even though the files are organised in a tree, it has no impact on the maintainability of the code base. Code can reference other code in other parts of the tree. You can easily create cycles in a language like C#, and organising files in trees makes no difference.
Most languages, however, enforce that library dependencies form a directed acyclic graph (i.e. if the data access library references the domain model, the domain model can't reference the data access library). The C# (and most other languages) compiler enforces what Robert C. Martin calls the Acyclic Dependencies Principle. Preventing cycles prevents spaghetti code, which is key to a maintainable code base.
(Ironically, one of the more controversial features of F# is actually one of its greatest strengths: It doesn't allow cycles.)
Tidiness #
Even so, I do understand the lure of organising code files in an elaborate hierarchy. It looks so neat.
Previously, I've touched on the related topic of consistency, and while I'm a bit of a neat freak myself, I have to realise that tidiness seems to be largely unrelated to the sustainability of a code base.
As another example in this category, I've seen more than one code base with consistently beautiful documentation. Every method was adorned with formal XML documentation with every input parameter as well as output described.
Every new phase in a method was delineated with another neat comment, nicely adorned with a 'comment frame' and aligned with other comments.
It was glorious.
Alas, that documentation sat on top of 750-line methods with a cyclomatic complexity above 50. The methods were so long that developers had to introduce artificial variable scopes to avoid naming collisions.
The reason I was invited to look at that code in the first place was that the organisation had trouble with maintainability, and they asked me to help.
It was neat, yet unmaintainable.
This discussion about tidiness may seem like a digression, but I think it's important to make the implicit explicit. If I'm not much mistaken, preference for order is a major reason that so many developers want to organise code files into hierarchies.
Organising principles #
What other motivations for file hierarchies could there be? How about the directory structure as an organising principle?
The two most common organising principles are those that I experimented with in the previous article:
- By technical role (Controller, View Model, DTO, etc.)
- By feature
A technical leader might hope that, by presenting a directory structure to team members, it imparts an organising principle on the code to be.
It may even do so, but is that actually a benefit?
It might subtly discourage developers from introducing code that doesn't fit into the predefined structure. If you organise code by technical role, developers might put most code in Controllers, producing mostly procedural Transaction Scripts. If you organise by feature, this might encourage duplication because developers don't have a natural place to put general-purpose code.
You can put truly shared code in the root folder, the counter-argument might be. This is true, but:
- This seems to be implicitly discouraged by the folder structure. After all, the hierarchy is there for a reason, right? Thus, any file you place in the root seems to suggest a failure of organisation.
- On the other hand, if you flaunt that not-so-subtle hint and put many code files in the root, what advantage does the hierarchy furnish?
In Information Distribution Aspects of Design Methodology David Parnas writes about documentation standards:
"standards tend to force system structure into a standard mold. A standard [..] makes some assumptions about the system. [...] If those assumptions are violated, the [...] organization fits poorly and the vocabulary must be stretched or misused."
(The above quote is on the surface about documentation standards, and I've deliberately butchered it a bit (clearly marked) to make it easier to spot the more general mechanism.)
In the same paper, Parnas describes the danger of making hard-to-change decisions too early. Applied to directory structure, the lesson is that you should postpone designing a file hierarchy until you know more about the problem. Start with a flat directory structure and add folders later, if at all.
Beyond files? #
My claim is that you don't need much in way of directory hierarchy. From this doesn't follow, however, that we may never leverage such options. Even though I left most of the example code for Code That Fits in Your Head in a single folder, I did add a specialised folder as an anti-corruption layer. Folders do have their uses.
"Why not take it to the extreme and place most code in a single file? If we navigate by "namespace view" and search, do we need all those files?"
Following a thought to its extreme end can shed light on a topic. Why not, indeed, put all code in a single file?
Curious thought, but possibly not new. I've never programmed in SmallTalk, but as I understand it, the language came with tooling that was both IDE and execution environment. Programmers would write source code in the editor, but although the code was persisted to disk, it may not have been as text files.
Even if I completely misunderstand how SmallTalk worked, it's not inconceivable that you could have a development environment based directly on a database. Not that I think that this sounds like a good idea, but it sounds technically possible.
Whether we do it one way or another seems mostly to be a question of tooling. What problems would you have if you wrote an entire C# (Java, Python, F#, or similar) code base as a single file? It becomes more difficult to look at two or more parts of the code base at the same time. Still, Visual Studio can actually give you split windows of the same file, but I don't know how it scales if you need multiple views over the same huge file.
Conclusion #
I recommend flat directory structures for code files. Put most code files in the root of a library or app. Of course, if your system is composed from multiple libraries (dependencies), each library has its own directory.
Subfolders aren't prohibited, only generally discouraged. Legitimate reasons to create subfolders may emerge as the code base evolves.
My misgivings about code file directory hierarchies mostly stem from the impact they have on developers' minds. This may manifest as magical thinking or cargo-cult programming: Erect elaborate directory structures to keep out the evil spirits of spaghetti code.
It doesn't work that way.

Comments
I don't think your perception that software is getting worse is wrong, Mark. I've been an Evernote user since 2011. And, for a good portion of those years, I've been a paid customer.
I'm certainly not alone in my perception that the application is becoming worse with each new release, to the point of, at times, becoming unusable. Syncing problems with the mobile version, weird changes in the UI that don't accomplish anything, general sluggishness, and, above all, not listening to the users regarding long-needed features.