ploeh blog danish software design
An example of state-based testing in Haskell
How do you do state-based testing when state is immutable? You use the State monad.
This article is an instalment in an article series about how to move from interaction-based testing to state-based testing. In the previous article, you saw an example of an interaction-based unit test written in C#. The problem that this article series attempts to address is that interaction-based testing can lead to what xUnit Test Patterns calls Fragile Tests, because the tests get coupled to implementation details, instead of overall behaviour.
My experience is that functional programming is better aligned with unit testing because functional design is intrinsically testable. While I believe that functional programming is no panacea, it still seems to me that we can learn many valuable lessons about programming from it.
People often ask me about F# programming: How do I know that my F# code is functional?
I sometimes wonder that myself, about my own F# code. One can certainly choose to ignore such a question as irrelevant, and I sometimes do, as well. Still, in my experience, asking such questions can create learning opportunities.
The best answer that I've found is: Port the F# code to Haskell.
Haskell enforces referential transparency via its compiler. If Haskell code compiles, it's functional. In this article, then, I take the problem from the previous article and port it to Haskell.
The code shown in this article is available on GitHub.
A function to connect two users #
In the previous article, you saw implementation and test coverage of a piece of software functionality to connect two users with each other. This was a simplification of the example running through my two Clean Coders videos, Church Visitor and Preserved in translation.
In contrast to the previous article, we'll start with the implementation of the System Under Test (SUT).
post :: Monad m => (a -> m (Either UserLookupError User)) -> (User -> m ()) -> a -> a -> m (HttpResponse User) post lookupUser updateUser userId otherUserId = do userRes <- first (\case InvalidId -> "Invalid user ID." NotFound -> "User not found.") <$> lookupUser userId otherUserRes <- first (\case InvalidId -> "Invalid ID for other user." NotFound -> "Other user not found.") <$> lookupUser otherUserId connect <- runExceptT $ do user <- ExceptT $ return userRes otherUser <- ExceptT $ return otherUserRes lift $ updateUser $ addConnection user otherUser return otherUser return $ either BadRequest OK connect
This is as direct a translation of the C# code as makes sense. If I'd only been implementing the desired functionality in Haskell, without having to port existing code, I'd designed the code differently.
This post function uses partial application as an analogy to dependency injection, but in order to enable potentially impure operations to take place, everything must happen inside of some monad. While the production code must ultimately run in the IO monad in order to interact with a database, tests can choose to run in another monad.
In the C# example, two dependencies are injected into the class that defines the Post method. In the above Haskell function, these two dependencies are instead passed as function arguments. Notice that both functions return values in the monad m.
The intent of the lookupUser argument is that it'll query a database with a user ID. It'll return the user if present, but it could also return a UserLookupError, which is a simple sum type:
data UserLookupError = InvalidId | NotFound deriving (Show, Eq)
If both users are found, the function connects the users and calls the updateUser function argument. The intent of this 'dependency' is that it updates the database. This is recognisably a Command, since its return type is m () - unit (()) is equivalent to void.
State-based testing #
How do you unit test such a function? How do you use Mocks and Stubs in Haskell? You don't; you don't have to. While the post method can be impure (when m is IO), it doesn't have to be. Functional design is intrinsically testable, but that proposition depends on purity. Thus, it's worth figuring out how to keep the post function pure in the context of unit testing.
While IO implies impurity, most common monads are pure. Which one should you choose? You could attempt to entirely 'erase' the monadic quality of the post function with the Identity monad, but if you do that, you can't verify whether or not updateUser was invoked.
While you could write an ad-hoc Mock using, for example, the Writer monad, it might be a better choice to investigate if something closer to state-based testing would be possible.
In an object-oriented context, state-based testing implies that you exercise the SUT, which mutates some state, and then you verify that the (mutated) state matches your expectations. You can't do that when you test a pure function, but you can examine the state of the function's return value. The State monad is an obvious choice, then.
A Fake database #
Haskell's State monad is parametrised on the state type as well as the normal 'value type', so in order to be able to test the post function, you'll have to figure out what type of state to use. The interactions implied by the post function's lookupUser and updateUser arguments are those of database interactions. A Fake database seems an obvious choice.
For the purposes of testing the post function, an in-memory database implemented using a Map is appropriate:
type DB = Map Integer User
This is simply a dictionary keyed by Integer values and containing User values. You can implement compatible lookupUser and updateUser functions with State DB as the Monad. The updateUser function is the easiest one to implement:
updateUser :: User -> State DB () updateUser user = modify $ Map.insert (userId user) user
This simply inserts the user into the database, using the userId as the key. The type of the function is compatible with the general requirement of User -> m (), since here, m is State DB.
The lookupUser Fake implementation is a bit more involved:
lookupUser :: String -> State DB (Either UserLookupError User) lookupUser s = do let maybeInt = readMaybe s :: Maybe Integer let eitherInt = maybe (Left InvalidId) Right maybeInt db <- get return $ eitherInt >>= maybe (Left NotFound) Right . flip Map.lookup db
First, consider the type. The function takes a String value as an argument and returns a State DB (Either UserLookupError User). The requirement is a function compatible with the type a -> m (Either UserLookupError User). This works when a is String and m is, again, State DB.
The entire function is written in do notation, where the inferred Monad is, indeed, State DB. The first line attempts to parse the String into an Integer. Since the built-in readMaybe function returns a Maybe Integer, the next line uses the maybe function to handle the two possible cases, converting the Nothing case into the Left InvalidId value, and the Just case into a Right value.
It then uses the State module's get function to access the database db, and finally attempt a lookup against that Map. Again, maybe is used to convert the Maybe value returned by Map.lookup into an Either value.
Happy path test case #
This is all you need in terms of Test Doubles. You now have test-specific lookupUser and updateUser functions that you can pass to the post function.
Like in the previous article, you can start by exercising the happy path where a user successfully connects with another user:
testProperty "Users successfully connect" $ \ user otherUser -> runStateTest $ do put $ Map.fromList [toDBEntry user, toDBEntry otherUser] actual <- post lookupUser updateUser (show $ userId user) (show $ userId otherUser) db <- get return $ isOK actual && any (elem otherUser . connectedUsers) (Map.lookup (userId user) db)
Here I'm inlining test cases as anonymous functions - this time expressing the tests as QuickCheck properties. I'll later return to the runStateTest helper function, but first I want to focus on the test body itself. It's written in do notation, and specifically, it runs in the State DB monad.
user and otherUser are input arguments to the property. These are both User values, since the test also defines Arbitrary instances for that type (not shown in this article; see the source code repository for details).
The first step in the test is to 'save' both users in the Fake database. This is easily done by converting each User value to a database entry:
toDBEntry :: User -> (Integer, User) toDBEntry = userId &&& id
Recall that the Fake database is nothing but an alias over Map Integer User, so the only operation required to turn a User into a database entry is to extract the key.
The next step in the test is to exercise the SUT, passing the test-specific lookupUser and updateUser Test Doubles to the post function, together with the user IDs converted to String values.
In the assert phase of the test, it first extracts the current state of the database, using the State library's built-in get function. It then verifies that actual represents a 200 OK value, and that the user entry in the database now contains otherUser as a connected user.
Missing user test case #
While there's one happy-path test case, there's four other test cases left. One of these is when the first user doesn't exist:
testProperty "Users don't connect when user doesn't exist" $ \ (Positive i) otherUser -> runStateTest $ do let db = Map.fromList [toDBEntry otherUser] put db let uniqueUserId = show $ userId otherUser + i actual <- post lookupUser updateUser uniqueUserId (show $ userId otherUser) assertPostFailure db actual
What ought to trigger this test case is that the 'first' user doesn't exist, even if the otherUser does exist. For this reason, the test inserts the otherUser into the Fake database.
Since the test is a QuickCheck property, i could be any positive Integer value - including the userId of otherUser. In order to properly exercise the test case, however, you'll need to call the post function with a uniqueUserId - thas it: an ID which is guaranteed to not be equal to the userId of otherUser. There's several options for achieving this guarantee (including, as you'll see soon, the ==> operator), but a simple way is to add a non-zero number to the number you need to avoid.
You then exercise the post function and, as a verification, call a reusable assertPostFailure function:
assertPostFailure :: (Eq s, Monad m) => s -> HttpResponse a -> StateT s m Bool assertPostFailure stateBefore resp = do stateAfter <- get let stateDidNotChange = stateBefore == stateAfter return $ stateDidNotChange && isBadRequest resp
This function verifies that the state of the database didn't change, and that the response value represents a 400 Bad Request HTTP response. This verification doesn't actually verify that the error message associated with the BadRequest case is the expected message, like in the previous article. This would, however, involve a fairly trivial change to the code.
Missing other user test case #
Similar to the above test case, users will also fail to connect if the 'other user' doesn't exist. The property is almost identical:
testProperty "Users don't connect when other user doesn't exist" $ \ (Positive i) user -> runStateTest $ do let db = Map.fromList [toDBEntry user] put db let uniqueOtherUserId = show $ userId user + i actual <- post lookupUser updateUser (show $ userId user) uniqueOtherUserId assertPostFailure db actual
Since this test body is so similar to the previous test, I'm not going to give you a detailed walkthrough. I did, however, promise to describe the runStateTest helper function:
runStateTest :: State (Map k a) b -> b runStateTest = flip evalState Map.empty
Since this is a one-liner, you could also write all the tests by simply in-lining that little expression, but I thought that it made the tests more readable to give this function an explicit name.
It takes any State (Map k a) b and runs it with an empty map. Thus, all State-valued functions, like the tests, must explicitly put data into the state. This is also what the tests do.
Notice that all the tests return State values. For example, the assertPostFailure function returns StateT s m Bool, of which State s Bool is an alias. This fits State (Map k a) b when s is Map k a, which again is aliased to DB. Reducing all of this, the tests are simply functions that return Bool.
Invalid user ID test cases #
Finally, you can also cover the two test cases where one of the user IDs is invalid:
testProperty "Users don't connect when user Id is invalid" $ \ s otherUser -> isIdInvalid s ==> runStateTest $ do let db = Map.fromList [toDBEntry otherUser] put db actual <- post lookupUser updateUser s (show $ userId otherUser) assertPostFailure db actual , testProperty "Users don't connect when other user Id is invalid" $ \ s user -> isIdInvalid s ==> runStateTest $ do let db = Map.fromList [toDBEntry user] put db actual <- post lookupUser updateUser (show $ userId user) s assertPostFailure db actual
Both of these properties take a String value s as input. When QuickCheck generates a String, that could be any String value. Both tests require that the value is an invalid user ID. Specifically, it mustn't be possible to parse the string into an Integer. If you don't constrain QuickCheck, it'll generate various strings, including e.g. "8" and other strings that can be parsed as numbers.
In the above "Users don't connect when user doesn't exist" test, you saw how one way to explicitly model constraints on data is to project a seed value in such a way that the constraint always holds. Another way is to use QuickCheck's built-in ==> operator to filter out undesired values. In this example, both tests employ the isIdInvalid function:
isIdInvalid :: String -> Bool isIdInvalid s = let userInt = readMaybe s :: Maybe Integer in isNothing userInt
Using isIdInvalid with the ==> operator guarantees that s is an invalid ID.
Summary #
While state-based testing may, at first, sound incompatible with strictly functional programming, it's not only possible with the State monad, but even, with good language support, easily done.
The tests shown in this article aren't concerned with the interactions between the SUT and its dependencies. Instead, they compare the initial state with the state after exercising the SUT. Comparing values, even complex data structures such as maps, tends to be trivial in functional programming. Immutable values typically have built-in structural equality (in Haskell signified by the automatic Eq type class), which makes comparing them trivial.
Now that we know that state-based testing is possible even with Haskell's enforced purity, it should be clear that we can repeat the feat in F#.
Code quality isn't software quality
A trivial observation made explicit.
You'd think that it's evident that code quality and software quality are two different things. Yet, I often see or hear arguments about one or the other that indicates to me that some people don't make that distinction. I wonder why; I do.
Software quality #
There's a school of thought leaders who advocate that, ultimately, we write code to solve problems, or to improve life, for people. I have nothing against that line of reasoning; it's just not one that I pursue much. Why should I use my energy on this message when someone like Dan North does it so much better than I could?
Dan North is far from the only person making the point that our employers, or clients, or end-users don't care about the code; he is, in my opinion, one of the best communicators in that field. It makes sense that, with that perspective on software development, you'd invent something like behaviour-driven development.
The evaluation criterion used in this discourse is one of utility. Does the software serve a purpose? Does it do it well?
In that light, quality software is software that serves its purpose beyond expectation. It rarely, if ever, crashes. It's easy to use. It's sufficiently responsive. It's pretty. It works both on-line and off-line. Attributes like that are externally observable qualities.
You can write quality software in many different languages, using various styles. When you evaluate the externally observable qualities of software, the code is invisible. It's not part of the evaluation.
It seems to me that some people try to make an erroneous conclusion from this premise. They'd say that since no employer, client, or end user evaluates the software based on the code that produced it, then no one cares about the code.
Code quality #
It's easy to refute that argument. All you have to do is to come up with a counter-example. You just have to find one person who cares about the code. That's easy.
You care about the code.
Perhaps you react negatively to that assertion. Perhaps you say: "No! I'm not one of those effete aesthetes who only program in Plankalkül." Fine. Maybe you're not the type who likes to polish the code; maybe you're the practical, down-to-earth type who just likes to get stuff done, so that your employer/client/end-user is happy.
Even so, I think that you still care about the code. Have you ever looked with bewilderment at a piece of code and thought: "Who the hell wrote this piece of shit!?" How many WTFs/m is your code?
I think every programmer cares about their code bases; if not in an active manner, then at least in a passive way. Bad code can seriously impede progress. I've seen more than one organisation effectively go out of business because of bad legacy code.
Code quality is when you care about the readability and malleability of the code. It's when you care about the code's ability to sustain the business, not only today, but also in the future.
Sustainable code #
I often get the impression that some people look at code quality and software quality as a (false) dichotomy.

Such arguments often seem to imply that you can't have one without sacrificing the other. You must choose.
The reality is, of course, that you can do both.
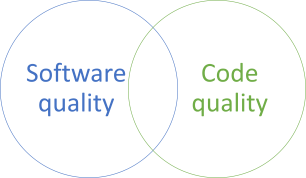
At the intersection between software and code quality the code sustains the business both now, and in the future.
Yes, you should write code such that it produces software that provides value here and now, but you should also do your best to enable it to provide value in the future. This is sustainable code. It's code that can sustain the organisation during its lifetime.
No gold-plating #
To be clear: this is not a call for gold plating or speculative generality. You probably can't predict the future needs of the stake-holders.
Quality code doesn't have to be able to perfectly address all future requirements. In order to be sustainable, though, it should be easy to modify in the future, or perhaps just easy to throw away and rewrite. I think a good start is to write humane code; code that fits in your brain.
At least, do your best to avoid writing legacy code.
Summary #
Software quality and code quality can co-exist. You can write quality code that compiles to quality software, but one doesn't imply the other. These are two independent quality dimensions.
An example of interaction-based testing in C#
An example of using Mocks and Stubs for unit testing in C#.
This article is an instalment in an article series about how to move from interaction-based testing to state-based testing. In this series, you'll be presented with some alternatives to interaction-based testing with Mocks and Stubs. Before we reach the alternatives, however, we need to establish an example of interaction-based testing, so that you have something against which you can compare those alternatives. In this article, I'll present a simple example, in the form of C# code.
The code shown in this article is available on GitHub.
Connect two users #
For the example, I'll use a simplified version of the example that runs through my two Clean Coders videos, Church Visitor and Preserved in translation.
The desired functionality is simple: implement a REST API that enables one user to connect to another user. You could imagine some sort of social media platform, or essentially any sort of online service where users might be interested in connecting with, or following, other users.
In essence, you could imagine that a user interface makes an HTTP POST request against our REST API:
POST /connections/42 HTTP/1.1
Content-Type: application/json
{
"otherUserId": 1337
}
Let's further imagine that we implement the desired functionality with a C# method with this signature:
public IHttpActionResult Post(string userId, string otherUserId)
We'll return to the implementation later, but I want to point out a few things.
First, notice that both userId and otherUserId are string arguments. While the above example encodes both IDs as numbers, essentially, both URLs and JSON are text-based. Following Postel's law, the method should also accept JSON like { "otherUserId": "1337" }. That's the reason the Post method takes string arguments instead of int arguments.
Second, the return type is IHttpActionResult. Don't worry if you don't know that interface. It's just a way to model HTTP responses, such as 200 OK or 400 Bad Request.
Depending on the input values, and the state of the application, several outcomes are possible:
| Other user | ||||
|---|---|---|---|---|
| Found | Not found | Invalid | ||
| User | Found | Other user | "Other user not found." |
"Invalid ID for other user." |
| Not found | "User not found." |
"User not found." |
"User not found." |
|
| Invalid | "Invalid user ID." |
"Invalid user ID." |
"Invalid user ID." |
|
"foo" that doesn't represent a number), then it doesn't matter if the other user exists. Likewise, even if the first user ID is well-formed, it might still be the case that no user with that ID exists in the database.
The assumption here is that the underlying user database uses integers as row IDs.
When both users are found, the other user should be returned in the HTTP response, like this:
HTTP/1.1 200 OK
Content-Type: application/json
{
"id": 1337,
"name": "ploeh",
"connections": [{
"id": 42,
"name": "fnaah"
}, {
"id": 2112,
"name": "ndøh"
}]
}
The intent is that when the first user (e.g. the one with the 42 ID) successfully connects to user 1337, a user interface can show the full details of the other user, including the other user's connections.
Happy path test case #
Since there's five distinct outcomes, you ought to write at least five test cases. You could start with the happy-path case, where both user IDs are well-formed and the users exist.
All tests in this article use xUnit.net 2.3.1, Moq 4.8.1, and AutoFixture 4.1.0.
[Theory, UserManagementTestConventions] public void UsersSuccessfullyConnect( [Frozen]Mock<IUserReader> readerTD, [Frozen]Mock<IUserRepository> repoTD, User user, User otherUser, ConnectionsController sut) { readerTD .Setup(r => r.Lookup(user.Id.ToString())) .Returns(Result.Success<User, IUserLookupError>(user)); readerTD .Setup(r => r.Lookup(otherUser.Id.ToString())) .Returns(Result.Success<User, IUserLookupError>(otherUser)); var actual = sut.Post(user.Id.ToString(), otherUser.Id.ToString()); var ok = Assert.IsAssignableFrom<OkNegotiatedContentResult<User>>( actual); Assert.Equal(otherUser, ok.Content); repoTD.Verify(r => r.Update(user)); Assert.Contains(otherUser.Id, user.Connections); }
To be clear, as far as Overspecified Software goes, this isn't a bad test. It only has two Test Doubles, readerTD and repoTD. My current habit is to name any Test Double with the TD suffix (for Test Double), instead of explicitly naming them readerStub and repoMock. The latter would have been more correct, though, since the Mock<IUserReader> object is consistently used as a Stub, whereas the Mock<IUserRepository> object is used only as a Mock. This is as it should be, because it follows the rule that you should use Mocks for Commands, Stubs for Queries.
IUserRepository.Update is, indeed a Command:
public interface IUserRepository { void Update(User user); }
Since the method returns void, unless it doesn't do anything at all, the only thing it can do is to somehow change the state of the system. The test verifies that IUserRepository.Update was invoked with the appropriate input argument.
This is fine.
I'd like to emphasise that this isn't the biggest problem with this test. A Mock like this verifies that a desired interaction took place. If IUserRepository.Update isn't called in this test case, it would constitute a defect. The software wouldn't have the desired behaviour, so the test ought to fail.
The signature of IUserReader.Lookup, on the other hand, implies that it's a Query:
public interface IUserReader { IResult<User, IUserLookupError> Lookup(string id); }
In C# and most other languages, you can't be sure that implementations of the Lookup method have no side effects. If, however, we assume that the code base in question obeys the Command Query Separation principle, then, by elimination, this must be a Query (since it's not a Command, because the return type isn't void).
For a detailed walkthrough of the IResult<S, E> interface, see my Preserved in translation video. It's just an Either with different terminology, though. Right is equivalent to SuccessResult, and Left corresponds to ErrorResult.
The test configures the IUserReader Stub twice. It's necessary to give the Stub some behaviour, but unfortunately you can't just use Moq's It.IsAny<string>() for configuration, because in order to model the test case, the reader should return two different objects for two different inputs.
This starts to look like Overspecified Software.
Ideally, a Stub should just be present to 'make happy noises' in case the SUT decides to interact with the dependency, but with these two Setup calls, the interaction is overspecified. The test is tightly coupled to how the SUT is implemented. If you change the interaction implemented in the Post method, you could break the test.
In any case, what the test does specify is that when you query the UserReader, it returns a Success object for both user lookups, a 200 OK result is returned, and the Update method was called with user.
Invalid user ID test case #
If the first user ID is invalid (i.e. not an integer) then the return value should represent 400 Bad Request and the message body should indicate as much. This test verifies that this is the case:
[Theory, UserManagementTestConventions] public void UsersFailToConnectWhenUserIdIsInvalid( [Frozen]Mock<IUserReader> readerTD, [Frozen]Mock<IUserRepository> repoTD, string userId, User otherUser, ConnectionsController sut) { Assert.False(int.TryParse(userId, out var _)); readerTD .Setup(r => r.Lookup(userId)) .Returns(Result.Error<User, IUserLookupError>( UserLookupError.InvalidId)); var actual = sut.Post(userId, otherUser.Id.ToString()); var err = Assert.IsAssignableFrom<BadRequestErrorMessageResult>(actual); Assert.Equal("Invalid user ID.", err.Message); repoTD.Verify(r => r.Update(It.IsAny<User>()), Times.Never()); }
This test starts with a Guard Assertion that userId isn't an integer. This is mostly an artefact of using AutoFixture. Had you used specific example values, then this wouldn't have been necessary. On the other hand, had you written the test case as a property-based test, it would have been even more important to explicitly encode such a constraint.
Perhaps a better design would have been to use a domain-specific method to check for the validity of the ID, but there's always room for improvement.
This test is more brittle than it looks. It only defines what should happen when IUserReader.Lookup is called with the invalid userId. What happens if IUserReader.Lookup is called with the Id associated with otherUser?
This currently doesn't matter, so the test passes.
The test relies, however, on an implementation detail. This test implicitly assumes that the implementation short-circuits as soon as it discovers that userId is invalid. What if, however, you'd made some performance measurements, and you'd discovered that in most cases, the software would run faster if you Lookup both users in parallel?
Such an innocuous performance optimisation could break the test, because the behaviour of readerTD is unspecified for all other cases than for userId.
Invalid ID for other user test case #
What happens if the other user ID is invalid? This unit test exercises that test case:
[Theory, UserManagementTestConventions] public void UsersFailToConnectWhenOtherUserIdIsInvalid( [Frozen]Mock<IUserReader> readerTD, [Frozen]Mock<IUserRepository> repoTD, User user, string otherUserId, ConnectionsController sut) { Assert.False(int.TryParse(otherUserId, out var _)); readerTD .Setup(r => r.Lookup(user.Id.ToString())) .Returns(Result.Success<User, IUserLookupError>(user)); readerTD .Setup(r => r.Lookup(otherUserId)) .Returns(Result.Error<User, IUserLookupError>( UserLookupError.InvalidId)); var actual = sut.Post(user.Id.ToString(), otherUserId); var err = Assert.IsAssignableFrom<BadRequestErrorMessageResult>(actual); Assert.Equal("Invalid ID for other user.", err.Message); repoTD.Verify(r => r.Update(It.IsAny<User>()), Times.Never()); }
Notice how the test configures readerTD twice: once for the Id associated with user, and once for otherUserId. Why does this test look different from the previous test?
Why is the first Setup required? Couldn't the arrange phase of the test just look like the following?
Assert.False(int.TryParse(otherUserId, out var _)); readerTD .Setup(r => r.Lookup(otherUserId)) .Returns(Result.Error<User, IUserLookupError>( UserLookupError.InvalidId));
If you wrote the test like that, it would resemble the previous test (UsersFailToConnectWhenUserIdIsInvalid). The problem, though, is that if you remove the Setup for the valid user, the test fails.
This is another example of how the use of interaction-based testing makes the tests brittle. The tests are tightly coupled to the implementation.
Missing users test cases #
I don't want to belabour the point, so here's the two remaining tests:
[Theory, UserManagementTestConventions] public void UsersDoNotConnectWhenUserDoesNotExist( [Frozen]Mock<IUserReader> readerTD, [Frozen]Mock<IUserRepository> repoTD, string userId, User otherUser, ConnectionsController sut) { readerTD .Setup(r => r.Lookup(userId)) .Returns(Result.Error<User, IUserLookupError>( UserLookupError.NotFound)); var actual = sut.Post(userId, otherUser.Id.ToString()); var err = Assert.IsAssignableFrom<BadRequestErrorMessageResult>(actual); Assert.Equal("User not found.", err.Message); repoTD.Verify(r => r.Update(It.IsAny<User>()), Times.Never()); } [Theory, UserManagementTestConventions] public void UsersDoNotConnectWhenOtherUserDoesNotExist( [Frozen]Mock<IUserReader> readerTD, [Frozen]Mock<IUserRepository> repoTD, User user, int otherUserId, ConnectionsController sut) { readerTD .Setup(r => r.Lookup(user.Id.ToString())) .Returns(Result.Success<User, IUserLookupError>(user)); readerTD .Setup(r => r.Lookup(otherUserId.ToString())) .Returns(Result.Error<User, IUserLookupError>( UserLookupError.NotFound)); var actual = sut.Post(user.Id.ToString(), otherUserId.ToString()); var err = Assert.IsAssignableFrom<BadRequestErrorMessageResult>(actual); Assert.Equal("Other user not found.", err.Message); repoTD.Verify(r => r.Update(It.IsAny<User>()), Times.Never()); }
Again, notice the asymmetry of these two tests. The top one passes with only one Setup of readerTD, whereas the bottom test requires two in order to pass.
You can add a second Setup to the top test to make the two tests equivalent, but people often forget to take such precautions. The result is Fragile Tests.
Post implementation #
In the spirit of test-driven development, I've shown you the tests before the implementation.
public class ConnectionsController : ApiController { public ConnectionsController( IUserReader userReader, IUserRepository userRepository) { UserReader = userReader; UserRepository = userRepository; } public IUserReader UserReader { get; } public IUserRepository UserRepository { get; } public IHttpActionResult Post(string userId, string otherUserId) { var userRes = UserReader.Lookup(userId).SelectError( error => error.Accept(UserLookupError.Switch( onInvalidId: "Invalid user ID.", onNotFound: "User not found."))); var otherUserRes = UserReader.Lookup(otherUserId).SelectError( error => error.Accept(UserLookupError.Switch( onInvalidId: "Invalid ID for other user.", onNotFound: "Other user not found."))); var connect = from user in userRes from otherUser in otherUserRes select Connect(user, otherUser); return connect.SelectBoth(Ok, BadRequest).Bifold(); } private User Connect(User user, User otherUser) { user.Connect(otherUser); UserRepository.Update(user); return otherUser; } }
This is a simplified version of the code shown towards the end of my Preserved in translation video, so I'll refer you there for a detailed explanation.
Summary #
The premise of Refactoring is that in order to be able to refactor, the "precondition is [...] solid tests". In reality, many development organisations have the opposite experience. When programmers attempt to make changes to how their code is organised, tests break. In xUnit Test Patterns this problem is called Fragile Tests, and the cause is often Overspecified Software. This means that tests are tightly coupled to implementation details of the System Under Test (SUT).
It's easy to inadvertently fall into this trap when you use Mocks and Stubs, even when you follow the rule of using Mocks for Commands and Stubs for Queries. In my experience, it's often the explicit configuration of Stubs that tend to make tests brittle. A Command represents an intentional side effect, and you want to verify that such a side effect takes place. A Query, on the other hand, has no side effect, so a black-box test shouldn't be concerned with any interactions involving Queries.
Yet, using an 'isolation framework' such as Moq, FakeItEasy, NSubstitute, and so on, will pull you towards overspecifying the interactions the SUT has with its Query dependencies.
How can we improve? One strategy is to move towards a more functional design, which is intrinsically testable. In the next article, you'll see how to rewrite both tests and implementation in Haskell.
From interaction-based to state-based testing
Indiscriminate use of Mocks and Stubs can lead to brittle test suites. A more functional design can make state-based testing easier, leading to more robust test suites.
The original premise of Refactoring was that in order to refactor, you must have a trustworthy suite of unit tests, so that you can be confident that you didn't break any functionality.
The idea is that you can change how the code is organised, and as long as you don't break any tests, all is good. The experience that most people seem to have, though, is that when they change something in the code, tests break."to refactor, the essential precondition is [...] solid tests"
This is a well-known test smell. In xUnit Test Patterns this is called Fragile Test, and it's often caused by Overspecified Software. Even if you follow the proper practice of using Mocks for Commands, Stubs for Queries, you can still end up with a code base where the tests are highly coupled to implementation details of the software.
The cause is often that when relying on Mocks and Stubs, test verification hinges on how the System Under Test (SUT) interacts with its dependencies. For that reason, we can call such tests interaction-based tests. For more information, watch my Pluralsight course Advanced Unit Testing.
Lessons from functional programming #
Another way to verify the outcome of a test is to inspect the state of the system after exercising the SUT. We can, quite naturally, call this state-based testing. In object-oriented design, this can lead to other problems. Nat Pryce has pointed out that state-based testing breaks encapsulation.
Interestingly, in his article, Nat Pryce concludes:
"I have come to think of object oriented programming as an inversion of functional programming. In a lazy functional language data is pulled through functions that transform the data and combine it into a single result. In an object oriented program, data is pushed out in messages to objects that transform the data and push it out to other objects for further processing."That's an impressively perceptive observation to make in 2004. I wish I was that perspicacious, but I only reached a similar conclusion ten years later.
Functional programming is based on the fundamental principle of referential transparency, which, among other things, means that data must be immutable. Thus, no objects change state. Instead, functions can return data that contains immutable state. In unit tests, you can verify that return values are as expected. Functional design is intrinsically testable; we can consider it a kind of state-based testing, although the states you'd be verifying are immutable return values.
In this article series, you'll see three different styles of testing, from interaction-based testing with Mocks and Stubs in C#, over strictly functional state-based testing in Haskell, to pragmatic state-based testing in F#, finally looping back to C# to apply the lessons from functional programming.
- An example of interaction-based testing in C#
- An example of state-based testing in Haskell
- An example of state based-testing in F#
- An example of state-based testing in C#
- A pure Test Spy
Summary #
Adopting a more functional design, even in a fundamentally object-oriented language like C# can, in my experience, lead to a more sustainable code base. Various maintenance tasks become easier, including unit tests. Functional programming, however, is no panacea. My intent with this article series is only to inspire; to show alternatives to the ways things are normally done. Adopting one of those alternatives could lead to better code, but you must still exercise context-specific judgement.
Asynchronous Injection
How to combine asynchronous programming with Dependency Injection without leaky abstractions.
C# has decent support for asynchronous programming, but it ultimately leads to leaky abstractions. This is often conspicuous when combined with Dependency Injection (DI). This leads to frequently asked questions around the combination of DI and asynchronous programming. This article outlines the problem and suggests an alternative.
The code base supporting this article is available on GitHub.
A synchronous example #
In this article, you'll see various stages of a small sample code base that pretends to implement the server-side behaviour of an on-line restaurant reservation system (my favourite example scenario). In the first stage, the code uses DI, but no asynchronous I/O.
At the boundary of the application, a Post method receives a Reservation object:
public class ReservationsController : ControllerBase { public ReservationsController(IMaîtreD maîtreD) { MaîtreD = maîtreD; } public IMaîtreD MaîtreD { get; } public IActionResult Post(Reservation reservation) { int? id = MaîtreD.TryAccept(reservation); if (id == null) return InternalServerError("Table unavailable"); return Ok(id.Value); } }
The Reservation object is just a simple bundle of properties:
public class Reservation { public DateTimeOffset Date { get; set; } public string Email { get; set; } public string Name { get; set; } public int Quantity { get; set; } public bool IsAccepted { get; set; } }
In a production code base, I'd favour a separation of DTOs and domain objects with proper encapsulation, but in order to keep the code example simple, here the two roles are combined.
The Post method simply delegates most work to an injected IMaîtreD object, and translates the return value to an HTTP response.
The code example is overly simplistic, to the point where you may wonder what is the point of DI, since it seems that the Post method doesn't perform any work itself. A slightly more realistic example includes some input validation and mapping between layers.
The IMaîtreD implementation is this:
public class MaîtreD : IMaîtreD { public MaîtreD(int capacity, IReservationsRepository repository) { Capacity = capacity; Repository = repository; } public int Capacity { get; } public IReservationsRepository Repository { get; } public int? TryAccept(Reservation reservation) { var reservations = Repository.ReadReservations(reservation.Date); int reservedSeats = reservations.Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return null; reservation.IsAccepted = true; return Repository.Create(reservation); } }
The protocol for the TryAccept method is that it returns the reservation ID if it accepts the reservation. If the restaurant has too little remaining Capacity for the requested date, it instead returns null. Regular readers of this blog will know that I'm no fan of null, but this keeps the example realistic. I'm also no fan of state mutation, but the example does that as well, by setting IsAccepted to true.
Introducing asynchrony #
The above example is entirely synchronous, but perhaps you wish to introduce some asynchrony. For example, the IReservationsRepository implies synchrony:
public interface IReservationsRepository { Reservation[] ReadReservations(DateTimeOffset date); int Create(Reservation reservation); }
In reality, though, you know that the implementation of this interface queries and writes to a relational database. Perhaps making this communication asynchronous could improve application performance. It's worth a try, at least.
How do you make something asynchronous in C#? You change the return type of the methods in question. Therefore, you have to change the IReservationsRepository interface:
public interface IReservationsRepository { Task<Reservation[]> ReadReservations(DateTimeOffset date); Task<int> Create(Reservation reservation); }
The Repository methods now return Tasks. This is the first leaky abstraction. From the Dependency Inversion Principle it follows that
The"clients [...] own the abstract interfaces"
MaîtreD class is the client of the IReservationsRepository interface, which should be designed to support the needs of that class. MaîtreD doesn't need IReservationsRepository to be asynchronous.
The change of the interface has nothing to with what MaîtreD needs, but rather with a particular implementation of the IReservationsRepository interface. Because this implementation queries and writes to a relational database, this implementation detail leaks into the interface definition. It is, therefore, a leaky abstraction.
On a more practical level, accommodating the change is easily done. Just add async and await keywords in appropriate places:
public async Task<int?> TryAccept(Reservation reservation) { var reservations = await Repository.ReadReservations(reservation.Date); int reservedSeats = reservations.Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return null; reservation.IsAccepted = true; return await Repository.Create(reservation); }
In order to compile, however, you also have to fix the IMaîtreD interface:
public interface IMaîtreD { Task<int?> TryAccept(Reservation reservation); }
This is the second leaky abstraction, and it's worse than the first. Perhaps you could successfully argue that it was conceptually acceptable to model IReservationsRepository as asynchronous. After all, a Repository conceptually represents a data store, and these are generally out-of-process resources that require I/O.
The IMaîtreD interface, on the other hand, is a domain object. It models how business is done, not how data should be accessed. Why should business logic be asynchronous?
It's hardly news that async and await is infectious. Once you introduce Tasks, it's async all the way!
That doesn't mean that asynchrony isn't one big leaky abstraction. It is.
You've probably already realised what this means in the context of the little example. You must also patch the Post method:
public async Task<IActionResult> Post(Reservation reservation) { int? id = await MaîtreD.TryAccept(reservation); if (id == null) return InternalServerError("Table unavailable"); return Ok(id.Value); }
Pragmatically, I'd be ready to accept the argument that this isn't a big deal. After all, you just replace all return values with Tasks, and add async and await keywords where they need to go. This hardly impacts the maintainability of a code base.
In C#, I'd be inclined to just acknowledge that, hey, there's a leaky abstraction. Moving on...
On the other hand, sometimes people imply that it has to be like this. That there is no other way.
Falsifiable claims like that often get my attention. Oh, really?!
Move impure interactions to the boundary of the system #
We can pretend that Task<T> forms a functor. It's also a monad. Monads are those incredibly useful programming abstractions that have been propagating from their origin in statically typed functional programming languages to more mainstream languages like C#.
In functional programming, impure interactions happen at the boundary of the system. Taking inspiration from functional programming, you can move the impure interactions to the boundary of the system.
In the interest of keeping the example simple, I'll only move the impure operations one level out: from MaîtreD to ReservationsController. The approach can be generalised, although you may have to look into how to handle pure interactions.
Where are the impure interactions in MaîtreD? They are in the two interactions with IReservationsRepository. The ReadReservations method is non-deterministic, because the same input value can return different results, depending on the state of the database when you call it. The Create method causes a side effect to happen, because it creates a row in the database. This is one way in which the state of the database could change, which makes ReadReservations non-deterministic. Additionally, Create also violates Command Query Separation (CQS) by returning the ID of the row it creates. This, again, is non-deterministic, because the same input value will produce a new return value every time the method is called. (Incidentally, you should design Create methods so that they don't violate CQS.)
Move reservations to a method argument #
The first refactoring is the easiest. Move the ReadReservations method call to the application boundary. In the above state of the code, the TryAccept method unconditionally calls Repository.ReadReservations to populate the reservations variable. Instead of doing this from within TryAccept, just pass reservations as a method argument:
public async Task<int?> TryAccept( Reservation[] reservations, Reservation reservation) { int reservedSeats = reservations.Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return null; reservation.IsAccepted = true; return await Repository.Create(reservation); }
This no longer compiles until you also change the IMaîtreD interface:
public interface IMaîtreD { Task<int?> TryAccept(Reservation[] reservations, Reservation reservation); }
You probably think that this is a much worse leaky abstraction than returning a Task. I'd be inclined to agree, but trust me: ultimately, this will matter not at all.
When you move an impure operation outwards, it means that when you remove it from one place, you must add it to another. In this case, you'll have to query the Repository from the ReservationsController, which also means that you need to add the Repository as a dependency there:
public class ReservationsController : ControllerBase { public ReservationsController( IMaîtreD maîtreD, IReservationsRepository repository) { MaîtreD = maîtreD; Repository = repository; } public IMaîtreD MaîtreD { get; } public IReservationsRepository Repository { get; } public async Task<IActionResult> Post(Reservation reservation) { var reservations = await Repository.ReadReservations(reservation.Date); int? id = await MaîtreD.TryAccept(reservations, reservation); if (id == null) return InternalServerError("Table unavailable"); return Ok(id.Value); } }
This is a refactoring in the true sense of the word. It just reorganises the code without changing the overall behaviour of the system. Now the Post method has to query the Repository before it can delegate the business decision to MaîtreD.
Separate decision from effect #
As far as I can tell, the main reason to use DI is because some impure interactions are conditional. This is also the case for the TryAccept method. Only if there's sufficient remaining capacity does it call Repository.Create. If it detects that there's too little remaining capacity, it immediately returns null and doesn't call Repository.Create.
In object-oriented code, DI is the most common way to decouple decisions from effects. Imperative code reaches a decision and calls a method on an object based on that decision. The effect of calling the method can vary because of polymorphism.
In functional programming, you typically use a functor like Maybe or Either to separate decisions from effects. You can do the same here.
The protocol of the TryAccept method already communicates the decision reached by the method. An int value is the reservation ID; this implies that the reservation was accepted. On the other hand, null indicates that the reservation was declined.
You can use the same sort of protocol, but instead of returning a Nullable<int>, you can return a Maybe<Reservation>:
public async Task<Maybe<Reservation>> TryAccept( Reservation[] reservations, Reservation reservation) { int reservedSeats = reservations.Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return Maybe.Empty<Reservation>(); reservation.IsAccepted = true; return reservation.ToMaybe(); }
This completely decouples the decision from the effect. By returning Maybe<Reservation>, the TryAccept method communicates the decision it made, while leaving further processing entirely up to the caller.
In this case, the caller is the Post method, which can now compose the result of invoking TryAccept with Repository.Create:
public async Task<IActionResult> Post(Reservation reservation) { var reservations = await Repository.ReadReservations(reservation.Date); Maybe<Reservation> m = await MaîtreD.TryAccept(reservations, reservation); return await m .Select(async r => await Repository.Create(r)) .Match( nothing: Task.FromResult(InternalServerError("Table unavailable")), just: async id => Ok(await id)); }
Notice that the Post method never attempts to extract 'the value' from m. Instead, it injects the desired behaviour (Repository.Create) into the monad. The result of calling Select with an asynchronous lambda expression like that is a Maybe<Task<int>>, which is a awkward combination. You can fix that later.
The Match method is the catamorphism for Maybe. It looks exactly like the Match method on the Church-encoded Maybe. It handles both the case when m is empty, and the case when m is populated. In both cases, it returns a Task<IActionResult>.
Synchronous domain logic #
At this point, you have a compiler warning in your code:
Warning CS1998 This async method lacks 'await' operators and will run synchronously. Consider using the 'await' operator to await non-blocking API calls, or 'await Task.Run(...)' to do CPU-bound work on a background thread.Indeed, the current incarnation of
TryAccept is synchronous, so remove the async keyword and change the return type:
public Maybe<Reservation> TryAccept( Reservation[] reservations, Reservation reservation) { int reservedSeats = reservations.Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return Maybe.Empty<Reservation>(); reservation.IsAccepted = true; return reservation.ToMaybe(); }
This requires a minimal change to the Post method: it no longer has to await TryAccept:
public async Task<IActionResult> Post(Reservation reservation) { var reservations = await Repository.ReadReservations(reservation.Date); Maybe<Reservation> m = MaîtreD.TryAccept(reservations, reservation); return await m .Select(async r => await Repository.Create(r)) .Match( nothing: Task.FromResult(InternalServerError("Table unavailable")), just: async id => Ok(await id)); }
Apart from that, this version of Post is the same as the one above.
Notice that at this point, the domain logic (TryAccept) is no longer asynchronous. The leaky abstraction is gone.
Redundant abstraction #
The overall work is done, but there's some tidying up remaining. If you review the TryAccept method, you'll notice that it no longer uses the injected Repository. You might as well simplify the class by removing the dependency:
public class MaîtreD : IMaîtreD { public MaîtreD(int capacity) { Capacity = capacity; } public int Capacity { get; } public Maybe<Reservation> TryAccept( Reservation[] reservations, Reservation reservation) { int reservedSeats = reservations.Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return Maybe.Empty<Reservation>(); reservation.IsAccepted = true; return reservation.ToMaybe(); } }
The TryAccept method is now deterministic. The same input will always return the same input. This is not yet a pure function, because it still has a single side effect: it mutates the state of reservation by setting IsAccepted to true. You could, however, without too much trouble refactor Reservation to an immutable Value Object.
This would enable you to write the last part of the TryAccept method like this:
return reservation.Accept().ToMaybe();
In any case, the method is close enough to be pure that it's testable. The interactions of TryAccept and any client code (including unit tests) is completely controllable and observable by the client.
This means that there's no reason to Stub it out. You might as well just use the function directly in the Post method:
public class ReservationsController : ControllerBase { public ReservationsController( int capacity, IReservationsRepository repository) { Capacity = capacity; Repository = repository; } public int Capacity { get; } public IReservationsRepository Repository { get; } public async Task<IActionResult> Post(Reservation reservation) { var reservations = await Repository.ReadReservations(reservation.Date); Maybe<Reservation> m = new MaîtreD(Capacity).TryAccept(reservations, reservation); return await m .Select(async r => await Repository.Create(r)) .Match( nothing: Task.FromResult(InternalServerError("Table unavailable")), just: async id => Ok(await id)); } }
Notice that ReservationsController no longer has an IMaîtreD dependency.
All this time, whenever you make a change to the TryAccept method signature, you'd also have to fix the IMaîtreD interface to make the code compile. If you worried that all of these changes were leaky abstractions, you'll be happy to learn that in the end, it doesn't even matter. No code uses that interface, so you can delete it.
Grooming #
The MaîtreD class looks fine, but the Post method could use some grooming. I'm not going to tire you with all the small refactoring steps. You can follow them in the GitHub repository if you're interested. Eventually, you could arrive at an implementation like this:
public class ReservationsController : ControllerBase { public ReservationsController( int capacity, IReservationsRepository repository) { Capacity = capacity; Repository = repository; maîtreD = new MaîtreD(capacity); } public int Capacity { get; } public IReservationsRepository Repository { get; } private readonly MaîtreD maîtreD; public async Task<IActionResult> Post(Reservation reservation) { return await Repository.ReadReservations(reservation.Date) .Select(rs => maîtreD.TryAccept(rs, reservation)) .SelectMany(m => m.Traverse(Repository.Create)) .Match(InternalServerError("Table unavailable"), Ok); } }
Now the Post method is just a single, composed asynchronous pipeline. Is it a coincidence that this is possible?
This is no coincidence. This top-level method executes in the 'Task monad', and a monad is, by definition, composable. You can chain operations together, and they don't all have to be asynchronous. Specifically, maîtreD.TryAccept is a synchronous piece of business logic. It's unaware that it's being injected into an asynchronous context. This type of design would be completely run of the mill in F# with its asynchronous workflows.
Summary #
Dependency Injection frequently involves I/O-bound operations. Those typically get hidden behind interfaces so that they can be mocked or stubbed. You may want to access those I/O-bound resources asynchronously, but with C#'s support for asynchronous programming, you'll have to make your abstractions asynchronous.
When you make the leaf nodes in your call graph asynchronous, that design change ripples through the entire code base, forcing you to be async all the way. One result of this is that the domain model must also accommodate asynchrony, although this is rarely required by the logic it implements. These concessions to asynchrony are leaky abstractions.
Pragmatically, it's hardly a big problem. You can use the async and await keywords to deal with the asynchrony, and it's unlikely to, in itself, cause a problem with maintenance.
In functional programming, monads can address asynchrony without introducing sweeping leaky abstractions. Instead of making DI asynchronous, you can inject desired behaviour into an asynchronous context.
Behaviour Injection, not Dependency Injection.
Comments
Hi Mark,
aren't you loading more responsibilities on the ReservationsController? Previously, it only had to delegate all the work to MaîtreD and return an appropriate result, now it additionally fetches reservations from the repository. You are also loading the handling of any errors the reservations repository might throw onto the controller, instead of handling them in the MaîtreD class.
You are also hard wiring a dependency on MaîtreD into the ReservationsController; I thought one of the advantages of DI were to avoid newing up dependencies to concrete implementations outside of a centralized "builder class".
Could you elaborate on these points? Thanks!
Ramon, thank you for writing. Am I loading more responsibilities on the Controller? Yes, I am. Too many? I don't think so.
To be fair, however, this example is unrealistically simplified (in order to make it easily understandable). There isn't much going on, overall, so one has to imagine that more things are happening than is actually the case. For instance, at the beginning of the example, so little is going on in the Controller that I think it'd be fair to ask why it's even necessary to distinguish between a Controller and a MaîtreD class.
Usually, I'd say that the responsibility of a Controller object is to facilitate the translation of what goes on at the boundary of the application and what happens in the domain model. Using the terminology of the ports and adapters architecture, you could say that a Controller's responsibility is to serve as an Adapter between the technology-agnostic domain model and the technology-specific SDKs you'll need to bring into play to communicate with the 'real world'. Talking to databases fits that responsibility, I think.
The MaîtreD class didn't handle any database errors before, so I don't agree that I've moved that responsibility.
When it comes to using a MaîtreD object from inside the Controller, I don't agree that I've 'hard-wired' it. It's not a dependency in the Dependency Injection sense; it's an implementation detail. Notice that it's a private class field.
Is it an 'advantage of DI' that you can "avoid newing up dependencies to concrete implementations outside of a centralized "builder class"?" How is that an advantage? Is that a goal?
In future articles, I'll discuss this sort of 'dependency elimination' in more details.
Mark, thanks for replying.
I assumed that some exception handling would be happening in the MaitreD class that would then migrate to the ReservationsController and you left it out for the sake of simplicity. But granted, that can still happen inside the respository class.
Let's imagine that for some reason, you want to write to the filesystem in addition to the database (eg. writing some reservation data like table number that can be printed and given to the customer). Following your reasoning, there would now be a reference to some IReservationPrinter in the Controller. It suddenly has to hold references to all data exchange classes that it was previously unaware of, only caring about the result MaîtreD was returning.
Maybe I didn't express myself properly: I thought Dependency Injection is a technique to resolve all implementation types at a single composition root. Of course this only applies to dependencies in the sense of DI, so where do you draw the line between implementation detail and dependency?
In any case I'm looking forward to reading more articles on this topic!
Ramon, in general when it comes to exception handling, you either handle exceptions at the source (i.e. in the Repository) or at the boundary of the application (which is typically done by frameworks already). I'm no fan of defensive coding.
"It suddenly has to hold references to all data exchange classes that it was previously unaware of"Yes, but now
MaîtreD doesn't have to do that. Is there anything inherently associated with business logic that stipulates that it handles data access?
The following line of argument may be increasingly difficult to relate to as time moves forward, and business becomes increasingly digital, but there once was a time when business logic was paper-based. In paper-based organisations, data would flow through a business in the shape of paper; typically as forms. Data would arrive at the desk of a clerk or domain expert who would add more data or annotations to a form, and put it in his or her out-box for later collection.
My point is that I see nothing inherent in business logic to stipulate that business objects should be responsible for data retrieval or persistence. I recommend Domain Modeling Made Functional if you're interested in a comprehensive treatment of this way of looking at modelling business logic.
"I thought Dependency Injection is a technique to resolve all implementation types at a single composition root."It is, and that still happens here. There are, however, fewer dependencies overall. I would argue that with the final design outlined here, the remaining dependency (
IReservationsRepository) is also, architecturally, the only real dependency of the application. The initial IMaîtreD dependency is, in my opinion, an implementation detail. Exposing it as a dependency makes the code more brittle, and harder to refactor, but that's what I'm going to cover in future articles.
Mark, I have to admit that I'm still not convinced (without having read the book you mentioned):
Expanding on your analogy, a clerk would maybe make a phone call or walk over to another desk if he needs more information regarding his current form (I know I do at my office). A maître d'hôtel would presumably open his book of reservations to check if he still has a table available and would write a new reservation in his book.
The MaîtreD doesn't need to know if the data it needs comes from the file system or a database or a web service (that's the responsibility of the repository class), all it cares about is that it needs some data. Currently, some other part of the system decides what data MaîtreD has to work with.
Again, I didn't have a look at the reading recommendation yet. Maybe I should. ;)
I definitely agree with Mark that the business logic (in the final version of MaîtreD.TryAccept) should be in a function that is pure and synchronous. However, I am also sympathetic to Ramon's argument.
There are two UIs for the application that I am currently building at work. The primary interface is over HTTP and uses web controllers just like in Mark's example. The second interface is a CLI (that is only accessable to administrators with phsyical access to the server). Suppose my application was also an on-line restaurant reservation system and that a reservation could be made with both UIs.
Looking back at the final implementation of ReservationsController.Post, the first three lines are independent of ControllerBase and would also need to be executed when accessing the system though the CLI. My understanding is that Ramon's primary suggestion is to move these three lines into MaîtreD.TryAccept. I am sympathetic to Ramon's argument in that I am in favor of extracting those three lines. However, I don't want them to be colocated with the final implimentatiion of MaîtreD.TryAccept.
In my mind, the single responsibility of ReservationsController.Post is to translate the result of the reseravation request into the expected type of response. That would be just the fourth line in the final implementation of this method. In terms of naming, I like Ramon's suggestion that the first three lines of ReservationsController.Post be moved to MaîtreD.TryAccept. But then I also want to move the final implementation of MaîtreD.TryAccept to a method on a different type. As we all know, naming is an impossible problem, so I don't have a good name for this new third type.
What do you think Ramon? Have I understood your concerns and suggested something that you could get behind?
What about you Mark? You said that there was
so little...going on in the Controller that I think it'd be fair to ask why it's even necessary to distinguish between a Controller and a MaîtreD class.
Would two UIs be sufficient motivation in your eyes to justify distinguishing between a Controller and a MaîtreD class?
Tyson, thank you for joining the discussion. By adding a particular problem (more than one user interface) to be addressed, you make the discussion more specific. I think this helps to clarify some issues.
Ramon wrote:
"I have to admit that I'm still not convinced"That's okay; you don't have to be. I rarely write articles with the explicit intent of telling people that they must do something, or that they should never do something else. While it does happen, this article isn't such an article. If it helps you address a problem, then take what you find useful. If it doesn't, then ignore it.
With Tyson's help, though, we can now discuss something more concrete. I think some of those observations identify a tender spot in my line of argument. In the initial version of ReservationsController, the only responsibility of the Post method was to translate from and to HTTP. That's a distinct separation of responsibility, so clearly preferable.
When I add the Repository dependency, I widen the scope of the ReservationsController's responsibility, which now includes 'all IO'. This does blur the demarcation of responsibility, but often still works out well in practice, I find. Still, it depends on how much other stuff is going on related to IO. If you have too much IO going on, another separation of responsibilities is in order.
I do find, however, that when implementing the same sort of software capability in different user interfaces, I need to specifically design for each user interface paradigm. A web-based user interface is quite different from a command-line interface, which is again different from a native application, or a voice-based interface, and so on. A web-based interface is, for example, stateless, whereas a native smart phone application would often be stateful. You can rarely reuse the 'user interface controller layer' for one type of application in a different type of application.
Even a command-line interface could be stateful by interactively asking a series of questions. That's such a different user interface paradigm that an object designed for one type of interaction is rarely reusable in another context.
What I do find is that fine-grained building blocks still compose. When TryAccept is a pure function, it's always composable. This means that my chance of being able to reuse it becomes much higher than if it's an object injected with various dependencies.
"a clerk would maybe make a phone call or walk over to another desk if he needs more information regarding his current form"Indeed, but how do you model this in software? A program doesn't have the degree of ad-hoc flexibility that people have. It can't just arbitrarily decide to make a phone call if it doesn't have a 'phone' dependency. Even when using Dependency Injection, you'll have to add that dependency to a business object. You'll have to explicitly write code to give it that capability, and even so, an injected dependency doesn't magically imbue a business object with the capability to make 'ad-hoc phone calls'. A dependency comes with specific methods you can call in order to answer specific questions.
Once you're adding code that enables an object to ask specific questions, you might as well just answer those questions up-front and pass the answer as method arguments. That's what this article's refactoring does. It knows that the MaîtreD object is going to ask about the existing reservations for the requested date, so it just passes that information as part of an 'execution context'.
"A maître d'hôtel would presumably open his book of reservations to check if he still has a table available and would write a new reservation in his book"That's a brilliant observation! This just once again demonstrates what Evans wrote in DDD, that insight about the domain arrive piecemeal. A maître d'hôtel clearly doesn't depend on any repository, but rather on the book of reservations. You can add that as a dependency, or pass it as a method argument. I'd lean toward doing the latter, because I'd tend to view a book as a piece of data.
Ultimately, if we are to take the idea of inversion of control seriously, we should, well, invert control. When we inject dependencies, we let the object with those dependencies control its interactions with them. Granted, those interactions are now polymorphic, but control isn't inverted.
If you truly want to invert control, then load data, pass it to functions, and persist the return values. In that way, functions have no control of where data comes from, or what happens to it afterwards. This keeps a software design supple.
Hi Mark, Thanks for your post, I think it's very valuable.
In the past, I had a situation when I was a junior software developer and just started working on a small, internal web application (ASP.NET MVC) to support HR processes in our company. At the time, I was discovering blogs like yours, or fsharpforfunandprofit.com and was especially fond of the sandwich architecture. I was preparing to refactor one of the controllers just like your example in this post (Controller retrieving necessary data from the repository, passing it to the pure business logic, then wrapping the results in a request). Unfortunately, My more experienced colleague said that it's a "fat controller antipattern" and that the controller can have only one line of code - redirecting the request to the proper business logic method. I wanted to explain to him that he is wrong, but couldn't find proper arguments, or examples.
Now I have them. This post is great for this particular purpose.
I guess it comes down to the amount of responsibilities the controller should have.
Marek named the fat controller antipattern. I remember reading about some years ago and it stuck, that's why I usually model my controllers to delegate the request to a worker class, maybe map a return value to a transfer object and wrap it all in some ActionResult. I can relate to the argument that all I/O should happen at the boundaries of the system, though I'm not seeing it on the controller's responsibility list, all the more so when I/O exceeds a simple database call.
If you have too much IO going on, another separation of responsibilities is in order.
I think that is what I was aiming for. The third type that Tyson is looking a name for could then be some kind of thin Data Access Layer, serving as a façade to encapsulate all calls to I/O, that can be injected into the MaîtreD class.
Isn't code flexibility usually modeled using conditionals? Assume we are a very important guest and our maître d'hôtel really wishes to make a reservation for us, but all tables are taken. He could decide to phone all currently known guests to ask for a confirmation, if some guest cannot make it, he could give the table to us.
Using the initial version of TryAccept, it would lead to something like this:
public async Task<int?> TryAccept(Reservation reservation)
{
if(await CheckTableAvailability(reservation))
{
reservation.IsAccepted = true;
return await Repository.Create(reservation);
}
else
{
return null;
}
}
private async Task<bool> CheckTableAvailability(Reservation reservation)
{
var reservations = await Repository.ReadReservations(reservation.Date);
int reservedSeats = reservations.Sum(r => r.Quantity);
if(Capacity < reservedSeats + reservation.Quantity)
{
foreach(var r in reservations)
{
if(!(await Telephone.AskConfirmation(r.Guest.PhoneNumber)))
{
//some guest cannot make it for his reservation
return true;
}
}
//all guests have confirmed their reservation - no table for us
return false;
}
return true;
}
That is assuming that MaîtreD has a dependency on both the Repository and a Telephone. Not the best code I've ever written, but it serves its purpose. If the dependency on Reservation is taken out of the MaîtreD, so could the dependency on Telephone. But then, you are deciding beforehand in the controller that MaîtreD might need to make a telephone call - that's business logic in the controller class and a weaker separation of concerns.
A maître d'hôtel clearly doesn't depend on any repository, but rather on the book of reservations. You can add that as a dependency, or pass it as a method argument. I'd lean toward doing the latter, because I'd tend to view a book as a piece of data.
And this is where I tend to disagree. The book of reservations in my eyes is owned and preciously guarded by the maître d'hôtel. Imagine some lowly garçon scribbling reservations in it. Unbelievable! Joking aside, the reservations in the book are pieces of data, no doubt about that - but I'd see the whole book as a resource owned by le maître and only him being able to request data from it. Of course, this depends on the model of the restaurant that I have in my mind, it might very well be different from yours - we didn't talk about a common model beforehand.
Apparently, I answered my own question when I moved the table availability check into its own private method. This way, a new dependency TableAvailabilityChecker can handle the availability check (complete with reservations book and phone calls), acting as a common data access layer.
I have created a repository, where I tried to follow the steps outlined in this blog post with the new dependency. After all refactorings the controller looks like this:
public class ReservationsController : ControllerBase
{
private readonly MaitreD _maitreD;
public ReservationsController(int capacity, IReservationsRepository repository, ITelephone telephone)
{
_maitreD = new MaitreD(capacity);
Repository = repository;
Telephone = telephone;
}
public IReservationsRepository Repository { get; }
public ITelephone Telephone { get; }
public async Task Post(Reservation reservation)
{
Reservation[] currentReservations = await Repository.ReadReservations(reservation.Date);
var confirmationCalls = currentReservations.Select(cr => Telephone.AskConfirmation(cr.Guest.PhoneNumber));
return _maitreD.CheckTableAvailability(currentReservations, reservation)
.Match(
some: r => new Maybe(r),
none: _maitreD.AskConfirmation(await Task.WhenAll(confirmationCalls), reservation)
)
.Match(
some: r => Ok(Repository.Create(_maitreD.Accept(r))),
none: new ContentResult { Content = "Table unavailable", StatusCode = StatusCodes.Status500InternalServerError } as ActionResult
);
}
}
During the refactorings, I was able to remove the TableAvailabilityChecker again; I'm quite happy that the maître d'hôtel is checking the table availability and asking for the confirmations with the resources that are given to him. I'm not so happy with the Task.WhenAll() part, but I don't know how to make this more readable and at the same time make the calls only if we need them.
All in all, I now think a bit differently about the controller responsibilities: Being at the boundary of the system, it is arguably the best place to make calls to external systems. If and how the information gathered from the outside is used however is still up to the business objects. Thanks, Mark, for the insight!
Thanks for writing this article. Doesn't testability suffer from turning the Maître d into an implementation detail of the ReservationsController? Now, we not only have to test for the controller's specific responsibilities but also for the behaviour that is implemented by the Maître d. Previously we could have provided an appropriate test double when instantiating the controller, knowing that the Maître d is tested and working. The resulting test classes would be more specific and focused. Is this a trade-off you made in favour of bringing the article's point across?
Max, thank you for writing. I don't think that testability suffers; on the contrary, I think that it improves. Once the MaîtreD class becomes deterministic, you no longer have to hide it behind a Test Double in order to be able to control its behaviour. You can control its behaviour simply by making sure that it receives the appropriate input arguments.
The Facade Tests that cover ReservationsController in the repository are, in my opinion, readable and maintainable.
I've started a new article series about this topic, since I knew it'd come up. I hope that these articles will help illustrate my position.
Hi, Mark! Thank you for this blog post.
I really like the way of composing effectful and pure code the post explains. But here are some things I keep wondering about.
1) Is it correct that — given this approach — pure code cannot call back into impure code. When I say call back I mean it in a general way: maybe invoking a lambda passed as an argument to a function, maybe invoking a method on an injected dependency — basically the specific mechanics of calling back are irrelevant in this case.
2) In case point 1) is actually correct, have you ever had in your practice a task where the "ban" on callbacks was too limiting/impractical?
To give a more specific example of scenarios I have in mind, let's get back to MaitreD for a second. Let's imagine the amount of reservations data grew too big to load all at once. As a result MaitreD needs an instance of ReservationRepository so it can first run some business logic and based on the outcome read only a small specific subset of reservations from the repository.
Or let's take a look at another imaginary scenario. Before confirming a reservation MaitreD must make a call to an external payment service to block a certain sum of money on the customer's card.
These are only quick examples off the top of my head. Maybe dealing with them is easy, I would still be really grateful if you could give a couple of scenarios where you found it hard or impractical to do without "callbacks" and if and how you eventually manage to overcome the complications.
Mykola, thank you for writing. Yes, it's correct that a pure function can't call an impure function. This means, among other things, that you can't use Dependency Injection in functional programming.
Is that rule impractical? It depends on the programming language. In Haskell, that rule is enforced by the compiler. You can't break that rule, but the language is also designed in such a way that there's plenty of better ways to do things. In Haskell, that rule isn't impractical.
In a language like F#, that rule is no longer enforced, and there's also fewer built-in alternatives. The general solution to the problem is to use a free monad, but while it's possible to use free monads in F#, it's not as idiomatic, and there's a compelling argument to be made that going with partial application as Dependency Injection is more practical.
It's also possible to employ free monads in C#, but it's really non-idiomatic and hard to understand.
Haskell has some other general-purpose solutions (e.g. the so-called mtl style), but the only type of architecture I'm aware of that translates to F# or C# is free monads.
Does this mean that the ideas of this article is impractical for real software?
I don't think so. Let's consider your examples:
That's a frequently asked question, but in reality, I have a hard time imagining that. How much data is a reservation? It's a date (8 bytes), a quantity (in reality, a single byte is enough to keep track of that), as well as a name and an email address. Let's assume that an email address is, on average, shorter than 30 characters, and a name is shorter than 50 characters. We'll assume that we save both strings in UTF-8. Most characters are probably still just going to be 1 byte, but let's be generous and assume 2 bytes per character. That's 169 bytes per reservation, but let's be even more generous and say 200 bytes per reservation."Let's imagine the amount of reservations data grew too big to load all at once."
What if we load 1,000 reservations? That's 200 kilobytes of memory. 10,000 reservations is 2 megabytes. That's about the size of an average web page. Is that too much data?
We routinely load web pages over the internet, and none but the Australians complain about the size.
My point is that I find it incredulous to claim that it'd be too much data if you need to load a couple of hundred of reservations in one go.
I can definitely imagine scenarios where you'd like to load reservations not only for the date in question, but also for surrounding dates. Even for a medium-sized restaurant, that's unlikely to be more than a few hundred, or perhaps a few thousand of reservations. That's not a lot of data. Most pictures on the WWW are bigger.
Just speculatively load extra data in one go. It's going to make your code much simpler, and is unlikely to affect performance if you're being smart about it. You can even consider to cache that data...
When it comes to your other question, I'll refer to a catch-phrase from the early days of large-scale web commerce (Pat Helland): take the money.
Don't make payment a blocking call. As soon as you have enough information to execute a purchase, kick it off as an asynchronous background job.
If a restaurant has that type of workflow that requires reservation of an amount on a credit card, you turn the business process into an asynchronous workflow. On the UI side, you make sure to reflect the current state of the system so that users don't try to reserve on dates that you already know are sold out. I show such a workflow in my functional architecture with F# Pluralsight course.
When a user makes a reservation, you take the reservation data and put it on a queue, and tell the user that you're working on it.
A background job receives the queued message and decides whether or not to accept the reservation. If it decides to accept it, it creates two other messages: one to reserve the money, and another a timeout.
Another background job receives the message to reserve the money on the credit card and attempts to do that. Once that's over, it reports success or failure by putting another message on a queue.
The reservation system receives the asynchronous message about the credit card and either commits or cancels the reservation. If it never gets such a message, the timeout message will eventually trigger a cancellation.
Each message handler can use the impure-pure-impure sandwich pattern, and in that way keep the business logic pure.
In my experience, you can often address issues like the ones you bring up by selecting an application architecture that best addresses those particular concerns. That'll make the implementation code simpler.
In fact, I'm often struggling to come up with an example scenario where something like a free monad would be necessary, because I always think to myself: Why would I do it that way? I'd just architect my application in this other way, and then the problem will go away by itself.
Hi Mark, I was just wondering - why is the controller asking its clients for a capacity, when it only uses it to imediately create a MaitreD? Should it not ask for the MaitreD in the first place, instead of sneakily conjuring it up in the constructor?
It feels like the controller owns the MaitreD, but the MaitreD represents pure and deterministic behaviour set up by its "capacity" dependency - and the capacity is only injected into the controller. So should it really be private?
Can't we just ask for the MaitreD, leave it public, forget about the "implementation detail" of a capacity, and be done with it?
Thanks!
votroto, thank you for writing. Injecting a concrete dependency is definitely an option. I'm currently working on a larger example code base that also has a MaitreD class, and in that code base I decided to inject that into the Controller instead of its constituent elements.
It's a trade-off; I don't see one option as more correct than the other. In the present article, the MaîtreD class is so simple that it only has a single dependency: capacity. In this case, it's a toss-up. Either you inject capacity, or you inject the entire MaîtreD class. In both cases, you have a single dependency in addition to that IReservationsRepository dependency. In this situation, I chose to follow the principle of least knowledge. By injecting only the capacity, the MaîtreD class is an implementation detail not exposed to the rest of the world.
In the larger example code base that I'm currently working on, the MaitreD class is more complex: it has several configuration values that determine its behaviour. If I wanted to keep the MaitreD class an implementation detail, the Controller constructor would look like this:
public ReservationsController( IReservationsRepository repository, TimeOfDay opensAt, TimeOfDay lastSeating, TimeSpan seatingDuration, IEnumerable<Table> tables) { Repository = repository; MaitreD = new MaitreD(opensAt, lastSeating, seatingDuration, tables); }
I don't think that this addresses any real concerns. If I ever decide to change the MaitreD constructor, I'd have to also change the ReservationsController constructor. Thus, while ReservationsController might not 'formally' depend on MaitreD, it still does so in practice. In that case I chose to inject MaitreD instead:
public ReservationsController( IReservationsRepository repository, MaitreD maitreD) { Repository = repository; MaitreD = maitreD; }
Don't read the above as an argument for one option over the other. I'm only trying to explain the deliberations I go through to arrive at a decision, one way or the other.
How to get the value out of the monad
How do I get the value out of my monad? You don't. You inject the desired behaviour into the monad.
A frequently asked question about monads can be paraphrased as: How do I get the value out of my monad? This seems to particularly come up when the monad in question is Haskell's IO monad, from which you can't extract the value. This is by design, but then beginners are often stumped on how to write the code they have in mind.
You can encounter variations of the question, or at least the underlying conceptual misunderstanding, with other monads. This seems to be particularly prevalent when object-oriented or procedural programmers start working with Maybe or Either. People really want to extract 'the value' from those monads as well, despite the lack of guarantee that there will be a value.
So how do you extract the value from a monad?
The answer isn't use a comonad, although it could be, for a limited set of monads. Rather, the answer is mu.
Unit containers #
Before I attempt to address how to work with monads, I think it's worthwhile to speculate on what misleads people into thinking that it makes sense to even contemplate extracting 'the value' from a monad. After all, you rarely encounter the question: How do I get the value out of my collection?
Various collections form monads, but everyone intuitively understand that there isn't a single value in a collection. Collections could be empty, or contain many elements. Collections could easily be the most ordinary monad. Programmers deal with collections all the time.
Yet, I think that most programmers don't realise that collections form monads. The reason for this could be that mainstream languages rarely makes this relationship explicit. Even C# query syntax, which is nothing but monads in disguise, hides this fact.
What happens, I think, is that when programmers first come across monads, they often encounter one of a few unit containers.
What's a unit container? I admit that the word is one I made up, because I couldn't detect existing terminology on this topic. The idea, though, is that it's a functor guaranteed to contain exactly one value. Since functors are containers, I call such types unit containers. Examples include Identity, Lazy, and asynchronous functors.
You can extract 'the value' from most unit containers (with IO being the notable exception from the rule). Trivially, you can get the item contained in an Identity container:
> Identity<string> x = new Identity<string>("bar"); > x.Item "bar"
Likewise, you can extract the value from lazy and asynchronous values:
> Lazy<int> x = new Lazy<int>(() => 42); > x.Value 42 > Task<int> y = Task.Run(() => 1337); > await y 1337
My theory, then, is that some programmers are introduced to the concept of monads via lazy or asynchronous computations, and that this could establish incorrect mental models.
Semi-containers #
There's another category of monad that we could call semi-containers (again, I'm open to suggestions for a better name). These are data containers that contain either a single value, or no value. In this set of monads, we find Nullable<T>, Maybe, and Either.
Unfortunately, Maybe implementations often come with an API that enables you to ask a Maybe object if it's populated or empty, and a way to extract the value from the Maybe container. This misleads many programmers to write code like this:
Maybe<int> id = // ... if (id.HasItem) return new Customer(id.Item); else throw new DontKnowWhatToDoException();
Granted, in many cases, people do something more reasonable than throwing a useless exception. In a specific context, it may be clear what to do with an empty Maybe object, but there are problems with this Tester-Doer approach:
- It doesn't compose.
- There's no systematic technique to apply. You always need to handle empty objects in a context-specific way.
If you throw an exception when the object is empty, you'll likely have to deal with that exception further up in the call stack.
If you return a magic value (like returning -1 when a natural number is expected), you again force all callers to check for that magic number.
If you set a flag that indicates that an object was empty, again, you put the burden on callers to check for the flag.
This leads to defensive coding, which, at best, makes the code unreadable.
Behaviour Injection #
Interestingly, programmers rarely take a Tester-Doer approach to working with collections. Instead, they rely on APIs for collections and arrays.
In C#, LINQ has been around since 2007, and most programmers love it. It's common knowledge that you can use the Select method to, for example, convert an array of numbers to an array of strings:
> new[] { 42, 1337, 2112, 90125 }.Select(i => i.ToString())
string[4] { "42", "1337", "2112", "90125" }
You can do that with all functors, including Maybe:
Maybe<int> id = // ... Maybe<Customer> c = id.Select(x => new Customer(x));
A previous article offers a slightly more compelling example:
var viewModel = repository.Read(id).Select(r => r.ToViewModel());
Common to all the three above examples is that instead of trying to extract a value from the monad (which makes no sense in the array example), you inject the desired behaviour into the context of the data container. What that eventually brings about depends on the monad in question.
In the array example, the behaviour being injected is that of turning a number into a string. Since this behaviour is injected into a collection, it's applied to every element in the source array.
In the second example, the behaviour being injected is that of turning an integer into a Customer object. Since this behaviour is injected into a Maybe, it's only applied if the source object is populated.
In the third example, the behaviour being injected is that of turning a Reservation domain object into a View Model. Again, this only happens if the original Maybe object is populated.
Composability #
The marvellous quality of a monad is that it's composable. You could, for example, start by attempting to parse a string into a number:
string candidate = // Some string from application boundary Maybe<int> idm = TryParseInt(candidate);
This code could be defined in a part of your code base that deals with user input. Instead of trying to get 'the value' out of idm, you can pass the entire object to other parts of the code. The next step, defined in a different method, in a different class, perhaps even in a different library, then queries a database to read a Reservation object corresponding to that ID - if the ID is there, that is:
Maybe<Reservation> rm = idm.SelectMany(repository.Read);
The Read method on the repository has this signature:
public Maybe<Reservation> Read(int id)
The Read method returns a Maybe<Reservation> object because you could pass any int to the method, but there may not be a row in the database that corresponds to that number. Had you used Select on idm, the return type would have been Maybe<Maybe<Reservation>>. This is a typical example of a nested functor, so instead, you use SelectMany, which flattens the functor. You can do this because Maybe is a monad.
The result at this stage is a Maybe<Reservation> object. If all goes according to plan, it's populated with a Reservation object from the database. Two things could go wrong at this stage, though:
- The
candidatestring didn't represent a number. - The database didn't contain a row for the parsed ID.
idm is empty.
You can now pass rm to another part of the code base, which then performs this step:
Maybe<ReservationViewModel> vm = rm.Select(r => r.ToViewModel());
Functors and monads are composable (i.e. 'chainable'). This is a fundamental trait of functors; they're (endo)morphisms, which, by definition, are composable. In order to leverage that composability, though, you must retain the monad. If you extract 'the value' from the monad, composability is lost.
For that reason, you're not supposed to 'get the value out of the monad'. Instead, you inject the desired behaviour into the monad in question, so that it stays composable. In the above example, repository.Read and r.ToViewModel() are behaviors injected into the Maybe monad.
Summary #
When we learn something new, there's always a phase where we struggle to understand a new concept. Sometimes, we may, inadvertently, erect a tentative, but misleading mental model of a concept. It seems to me that this happens to many people while they're grappling with the concept of functors and monads.
One common mental wrong turn that many people seem to take is to try to 'get the value out of the monad'. This seems to be particularly common with IO in Haskell, where the issue is a frequently asked question.
I've also reviewed enough F# code to have noticed that people often take the imperative, Tester-Doer road to 'a option. That's the reason this article uses a majority of its space on various Maybe examples.
In a future article, I'll show a more complete and compelling example of behaviour injection.
Comments
Hi Mark, was very interested in your post as I do try and use Option Monads in my code, and I think I understand the point you are making about not thinking of an optional value as something that is composable. However, I recently had a couple of situations where I reluctantly had to check the value, would really appreciate any thoughts you may have?
The first example was where I have a UI and the user may specify a Latitude and a Longitude. The user may not yet have specified both values, so each is held as an Option
Having read your article, I realise I could change this to a Select statement on latitude, but that lambda would still need to check longitude.HasValue. Should I combine the two options somehow before doing a single Select?
The second example again relates to a UI where the user can enter values in a grid, or leave a row blank. I would like to calculate the mean, standard deviation and root mean square of the values, and normally all these functions would have the signature: double Mean(ICollection<double> values)
If I keep this then I need a function like
if(latitude.HasValue && longitude.HasValue)
Bearing = CalculateRhumbBearing(latitude.Value, longitude.Value, fixedLatitude, fixedLongitude).ToOptionMonad();
else
Bearing = OptionMonad<double>.None;
foreach(var item in values)
{
if(item.HasValue)
{
yield return item.Value;
}
}
Or some equivalent Where/Select combination. Can you advise me please, how you recommend transforming an IEnumerable<OptionMonad<X>> to an enumerable<X>? Or should I write a signature overload double Mean(ICollection<OptionMonad<double>> possibleValues) and ditto for SD and RMS?
Thanks, Sean
Sean, thank you for writing. The first example you give is quite common, and is easily addressed with using the applicative or monadic capabilities of Maybe. Often, in a language like C#, it's easiest to use monadic bind (in C# called SelectMany):
Bearing = latitude .SelectMany(lat => longitude .Select(lon => CalculateRhumbBearing(lat, lon, fixedLatitude, fixedLongitude)));
If you find code like that disagreeable, you can also write it with query syntax:
Bearing = from lat in latitude from lon in longitude select CalculateRhumbBearing(lat, lon, fixedLatitude, fixedLongitude);
Here, Bearing is a Maybe value. As you can see, in neither of the above alternatives is it necessary to check and extract the values. Bearing will be populated when both latitude and longitude are populated, and empty otherwise.
Regarding the other question, being able to filter out empty values from a collection is a standard operation in both F# and Haskell. In C#, you can write it like this:
public static IEnumerable<T> Choose<T>(this IEnumerable<IMaybe<T>> source) { return source.SelectMany(m => m.Match(new T[0], x => new[] { x })); }
This example is based on the Church-encoded Maybe, which is currently my favourite implementation. I decided to call the method Choose, as this is also the name it has in F#. In Haskell, this function is called catMaybes.
Hi Mark, did you ever think about publishing a Library containing all these types missing in .net Framework like Either? Or can you recommend an existing library?
Achim, thank you for writing. The thought has crossed my mind, but my position on this question seems to be changing.
Had you asked me one or two years ago, I'd have answered that I hadn't seriously considered doing that, and that I saw little reason to do so. There is, as far as I can tell, plenty of such libraries out there, although I can't recommend any in particular. This seems to be something that many people create as part of a learning exercise. It seems to be a rite of passage for many people, similarly to developing a Dependency Injection container, or an ORM.
Besides, a reusable library would mean another dependency that your code would have to take on.
These days, however, I'm beginning to reconsider my position. It seems that no such library is emerging as dominant, and some of the types involved (particularly Maybe) would really be useful.
Ideally, these types ought be in the .NET Base Class Library, but perhaps a second-best alternative would be to put them in a commonly-used shared library.
Hi Mark, thank you for the interesting article series.
Can you maybe provide guidance of how asynchronous operations can become part of a chain of operations? How would the 'functor flattening' be combined with the built Task/Task<T> types? Extending your example, how would you go about if we would like to enrich the reservation retrieved from repository with that day's special, which happens to be async:
Task<ReservationWithMenuSuggestion> EnrichWithSpecialOfTheDayAsync(Reservation reservation)
I tried with your Church encoded Maybe implementation, but I got stuck with the Task<T> wrapping/unwrapping/awaiting.
Ralph, thank you for writing. Please see if my new article Asynchronous Injection answers your question.
Hi Mark, I'm curious what do you think about this approach to monads - Maybe monad through async/await in C#
Dominik, thank you for writing. That's a clever article. As far as I can tell, the approach is similar to Nick Palladinos' Eff library. You can see how he rewrote one of my sample applications using it.
I've no personal experience with this approach, so I could easily be wrong in my assessment. Nick reports that he's had some success getting other people on board with such an approach, because the resulting user code looks like idiomatic C#. That is, I think, one compelling argument.
What I do find less appealing, however, is that, if I understand this correctly, the C# compiler enables you to mix, or interleave, disparate effects. As long as your method returns an awaitable object, you can await true asynchronous tasks, bind Maybe values, and conceivably invoke other effectful operations all in the same method - and you wouldn't be able to tell from the return type what to expect.
In my opinion, one of the most compelling benefits of modelling with universal abstractions is that they provide excellent encapsulation. You can use the type system to communicate the pre- and post-conditions of an operation.
If I see an operation that returns Maybe<User>, I expect that it may or may not return a User object. If I see a return type of Task<User>, I expect that I'm guaranteed to receive a User object, but that this'll happen asynchronously. Only if I see something like Task<Maybe<User>> do I expect the combination of those two effects.
My concern with making Maybe awaitable is that this enables one to return Maybe<User> from a method, but still make the implementation asynchronous (e.g. by querying a database for the user). That effect is now hidden, which in my view break encapsulation because you now have to go and read the implementation code in order to discover that this is taking place.
Mark, thanks for useful respond!
You are absolutely true that awaiting Maybe that have Task have side effects not visible to invoker. I agree that this is the smell I felt but you gave me the source of it.
Better abstractions revisited
How do you design better abstractions? A retrospective look on an old article for object-oriented programmers.
About a decade ago, I had already been doing test-driven development (TDD) and used Dependency Injection for many years, but I'd started to notice some patterns about software design. I'd noticed that interfaces aren't abstractions and that TDD isn't a design methodology. Sometimes, I'd arrive at interfaces that turned out to be good abstractions, but at other times, the interfaces I created seemed to serve no other purpose than enabling unit testing.
In 2010 I thought that I'd noticed some patterns for good abstractions, so I wrote an article called Towards better abstractions. I still consider it a decent attempt at communicating my findings, but I don't think that I succeeded. My thinking on the subject was still too immature, and I lacked a proper vocabulary.
While I had hoped that I would be able to elaborate on such observations, and perhaps turn them into heuristics, my efforts soon after petered out. I moved on to other things, and essentially gave up on this particular research programme. Years later, while trying to learn category theory, I suddenly realised that mathematical disciplines like category theory and abstract algebra could supply the vocabulary. After some further work, I started publishing a substantial and long-running article series called From design patterns to category theory. It goes beyond my initial attempt, but it finally enabled me to crystallise those older observations.
In this article, I'll revisit that old article, Towards better abstractions, and translate the vague terminology I used then, to the terminology presented in From design patterns to category theory.
The thrust of the old article is that if you can create a Composite or a Null Object from an interface, then it's likely to be a good abstraction. I still consider that a useful rule of thumb.
When can you create a Composite? When the abstraction gives rise to a monoid. When can you create a Null Object? When the abstraction gives rise to a monoid.
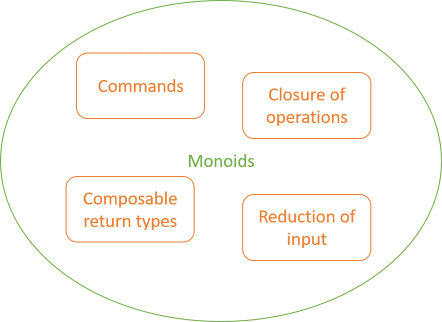
All the 'API shapes' I'd identified in Towards better abstractions form monoids.
Commands #
A Command seems to be universally identified by a method typically called Execute:
public void Execute()
From unit isomorphisms we know that methods with the void return type are isomorphic to (impure) functions that return unit, and that unit forms a monoid.
Furthermore, we know from function monoids that methods that return a monoid themselves form monoids. Therefore, Commands form monoids.
In early 2011 I'd already explicitly noticed that Commands are composable. Now I know the deeper reason for this: they're monoids.
Closure of operations #
In Domain-Driven Design, Eric Evans discusses the benefits of designing APIs that exhibit closure of operations. This means that a method returns the same type as all its input arguments. The simplest example is the one that I show in the old article:
public static T DoIt(T x)
That's just an endomorphism, which forms a monoid.
Another variation is a method that takes two arguments:
public static T DoIt(T x, T y)
This is a binary operation. While it's certainly a magma, in itself it's not guaranteed to be a monoid. In fact, Evans' colour-mixing example is only a magma, but not a monoid. You can, however, also view this as a special case of the reduction of input shape, below, where the 'extra' arguments just happen to have the same type as the return type. In that interpretation, such a method still forms a monoid, but it's not guaranteed to be meaningful. (Just like modulo 31 addition forms a monoid; it's hardly useful.)
The same sort of argument goes for methods with closure of operations, but more input arguments, like:
public static T DoIt(T x, T y, T z)
This sort of method is, however, rare, unless you're working in a stringly typed code base where methods look like this:
public static string DoIt(string x, string y, string z)
That's a different situation, though, because those strings should probably be turned into domain types that properly communicate their roles. Once you do that, you'll probably find that the method arguments have different types.
In any case, regardless of cardinality, you can view all methods with closure of operations as special cases of the reduction of input shape below.
Reduction of input #
This is the part of the original article where my struggles with vocabulary began in earnest. The situation is when you have a method that looks like this, perhaps as an interface method:
public interface IInputReducer<T1, T2, T3> { T1 DoIt(T1 x, T2 y, T3 z); }
In order to stay true to the terminology of my original article, I've named this reduction of input generic example IInputReducer. The reason I originally called it reduction of input is that such a method takes a set of input types as arguments, but only returns a value of a type that's a subset of the set of input types. Thus, the method looks like it's reducing the range of input types to a single one of those types.
A realistic example could be a piece of HTTP middleware that defines an action filter as an interface that you can implement to intercept each HTTP request:
public interface IActionFilter { Task<HttpResponseMessage> ExecuteActionFilterAsync( HttpActionContext actionContext, CancellationToken cancellationToken, Task<HttpResponseMessage> continuation); }
This is a slightly modified version of an earlier version of the ASP.NET Web API. Notice that in this example, it's not the first argument's type that doubles as the return type, but rather the third and last argument. The reduction of input 'shape' can take an arbitrary number of arguments, and any of the argument types can double as a return type, regardless of position.
Returning to the generic IInputReducer example, you can easily make a Composite of it:
public class CompositeInputReducer<T1, T2, T3> : IInputReducer<T1, T2, T3> { private readonly IInputReducer<T1, T2, T3>[] reducers; public CompositeInputReducer(params IInputReducer<T1, T2, T3>[] reducers) { this.reducers = reducers; } public T1 DoIt(T1 x, T2 y, T3 z) { var acc = x; foreach (var reducer in reducers) acc = reducer.DoIt(acc, y, z); return acc; } }
Notice that you call DoIt on all the composed reducers. The arguments that aren't part of the return type, y and z, are passed to each call to DoIt unmodified, whereas the T1 value x is only used to initialise the accumulator acc. Each call to DoIt also returns a T1 object, so the acc value is updated to that object, so that you can use it as an input for the next iteration.
This is an imperative implementation, but as you'll see below, you can also implement the same behaviour in a functional manner.
For the sake of argument, pretend that you reorder the method arguments so that the method looks like this:
T1 DoIt(T3 z, T2 y, T1 x);
From Uncurry isomorphisms you know that a method like that is isomorphic to a function with the type 'T3 -> 'T2 -> 'T1 -> 'T1 (F# syntax). You can think of such a curried function as a function that returns a function that returns a function: 'T3 -> ('T2 -> ('T1 -> 'T1)). The rightmost function 'T1 -> 'T1 is clearly an endomorphism, and you already know that an endomorphism gives rise to a monoid. Finally, Function monoids informs us that a function that returns a monoid itself forms a monoid, so 'T2 -> ('T1 -> 'T1) forms a monoid. This argument applies recursively, because if that's a monoid, then 'T3 -> ('T2 -> ('T1 -> 'T1)) is also a monoid.
What does that look like in C#?
In the rest of this article, I'll revert the DoIt method signature to T1 DoIt(T1 x, T2 y, T3 z);. The monoid implementation looks much like the endomorphism code. Start with a binary operation:
public static IInputReducer<T1, T2, T3> Append<T1, T2, T3>( this IInputReducer<T1, T2, T3> r1, IInputReducer<T1, T2, T3> r2) { return new AppendedReducer<T1, T2, T3>(r1, r2); } private class AppendedReducer<T1, T2, T3> : IInputReducer<T1, T2, T3> { private readonly IInputReducer<T1, T2, T3> r1; private readonly IInputReducer<T1, T2, T3> r2; public AppendedReducer( IInputReducer<T1, T2, T3> r1, IInputReducer<T1, T2, T3> r2) { this.r1 = r1; this.r2 = r2; } public T1 DoIt(T1 x, T2 y, T3 z) { return r2.DoIt(r1.DoIt(x, y, z), y, z); } }
This is similar to the endomorphism Append implementation. When you combine two IInputReducer objects, you receive an AppendedReducer that implements DoIt by first calling DoIt on the first object, and then using the return value from that method call as the input for the second DoIt method call. Notice that y and z are just 'context' variables used for both reducers.
Just like the endomorphism, you can also implement the identity input reducer:
public class IdentityInputReducer<T1, T2, T3> : IInputReducer<T1, T2, T3> { public T1 DoIt(T1 x, T2 y, T3 z) { return x; } }
This simply returns x while ignoring y and z. The Append method is associative, and the IdentityInputReducer is both left and right identity for the operation, so this is a monoid. Since monoids accumulate, you can also implement an Accumulate extension method:
public static IInputReducer<T1, T2, T3> Accumulate<T1, T2, T3>( this IReadOnlyCollection<IInputReducer<T1, T2, T3>> reducers) { IInputReducer<T1, T2, T3> identity = new IdentityInputReducer<T1, T2, T3>(); return reducers.Aggregate(identity, (acc, reducer) => acc.Append(reducer)); }
This implementation follows the overall implementation pattern for accumulating monoidal values: start with the identity and combine pairwise. While I usually show this in a more imperative form, I've here used a proper functional implementation for the method.
The IInputReducer object returned from that Accumulate function has exactly the same behaviour as the CompositeInputReducer.
The reduction of input shape forms another monoid, and is therefore composable. The Null Object is the IdentityInputReducer<T1, T2, T3> class. If you set T1 = T2 = T3, you have the closure of operations 'shapes' discussed above; they're just special cases, so form at least this type of monoid.
Composable return types #
The original article finally discusses methods that in themselves don't look composable, but turn out to be so anyway, because their return types are composable. Without knowing it, I'd figured out that methods that return monoids are themselves monoids.
In 2010 I didn't have the vocabulary to put this into specific language, but that's all it says.
Summary #
In 2010 I apparently discovered an ad-hoc, informally specified, vaguely glimpsed, half-understood description of half of abstract algebra.
Riffs on Greenspun's tenth rule aside, things clicked for me once I started to investigate what category theory was about, and why it seemed so closely linked to Haskell. That's one of the reasons I started writing the From design patterns to category theory article series.
The patterns I thought that I could see in 2010 all form monoids, but there are many other universal abstractions from mathematics that apply to programming as well.
Some thoughts on anti-patterns
What's an anti-pattern? Are there rules to identify them, or is it just name-calling? Before I use the term, I try to apply some rules of thumb.
It takes time to write a book. Months, even years. It took me two years to write the first edition of Dependency Injection in .NET. The second edition of Dependency Injection in .NET is also the result of much work; not so much by me, but by my co-author Steven van Deursen.
When you write a book single-handedly, you can be as opinionated as you'd like. When you have a co-author, regardless of how much you think alike, there's bound to be some disagreements. Steven and I agreed about most of the changes we'd like to make to the second edition, but each of us had to yield or compromise a few times.
An interesting experience has been that on more than one occasion where I've reluctantly had to yield to Steven, over the time, I've come to appreciate his position. Two minds think better than one.
Ambient Context #
One of the changes that Steven wanted to make was that he wanted to change the status of the Ambient Context pattern to an anti-pattern. While I never use that pattern myself, I included it in the first edition in the spirit of the original Design Patterns book. The Gang of Four made it clear that the patterns they'd described weren't invented, but rather discovered:
The spirit, as I understand it, is to identify solutions that already exist, and catalogue them. When I wrote the first edition of my book, I tried to do that as well."We have included only designs that have been applied more than once in different systems."
I'd noticed what I eventually named the Ambient Context pattern several places in the .NET Base Class Library. Some of those APIs are still around today. Thread.CurrentPrincipal, CultureInfo.CurrentCulture, thread-local storage, HttpContext.Current, and so on.
None of these really have anything to do with Dependency Injection (DI), but people sometimes attempt to use them to solve problems similar to the problems that DI addresses. For that reason, and because the pattern was so prevalent, I included it in the book - as a pattern, not an anti-pattern.
Steven wanted to make it an anti-pattern, and I conceded. I wasn't sure I was ready to explicitly call it out as an anti-pattern, but I agreed to the change. I'm becoming increasingly happy that Steven talked me into it.
Pareto efficiency #
I've heard said of me that I'm one of those people who call everything I don't like an anti-pattern. I don't think that's true.
I think people's perception of me is skewed because even today, the most visited page (my greatest hit, if you will) is an article called Service Locator is an Anti-Pattern. (It concerns me a bit that an article from 2010 seems to be my crowning achievement. I hope I haven't peaked yet, but the numbers tell a different tale.)
While I've used the term anti-pattern in other connections, I prefer to be conservative with my use of the word. I tend to use it only when I feel confident that something is, indeed, an anti-pattern.
What's an anti-pattern? AntiPatterns defines it like this:
As definitions go, it's quite amphibolous. Is it the problem that generates negative consequences? Hardly. In the context, it's clear that it's the solution that causes problems. In any case, just because it's in a book doesn't necessarily make it right, but I find it a good start."An AntiPattern is a literary form that describes a commonly occurring solution to a problem that generates decidedly negative consequences."
I think that the phrase decidedly negative consequences is key. Most solutions come with some disadvantages, but in order for a 'solution' to be an anti-pattern, the disadvantages must clearly outweigh any advantages produced.
I usually look at it another way. If I can solve the problem in a different way that generates at least as many advantages, but fewer disadvantages, then the first 'solution' might be an anti-pattern. This way of viewing the problem may stem from my background in economics. In that perspective, an anti-pattern simply isn't Pareto optimal.
Falsifiability #
Another rule of thumb I employ to determine whether a solution could be an anti-pattern is Popper's concept of falsifiability. As a continuation of the Pareto efficiency perspective, an anti-pattern is a 'solution' that you can improve without any (significant) trade-offs.
That turns claims about anti-patterns into falsifiable statements, which I consider is the most intellectually honest way to go about claiming that things are bad.
Take, for example, the claim that Service Locator is an anti-pattern. In light of Pareto efficiency, that's a falsifiable claim. All you have to do to prove me wrong is to present a situation where Service Locator solves a problem, and I can't come up with a better solution.
I made the claim about Service Locator in 2010, and so far, no one has been able to present such a situation, even though several have tried. I'm fairly confident making that claim.
This way of looking at the term anti-pattern, however, makes me wary of declaiming solutions anti-patterns just because I don't like them. Could there be a counter-argument, some niche scenario, where the pattern actually couldn't be improved without trade-offs?
I didn't take it lightly when Steven suggested making Ambient Context an anti-pattern.
Preliminary status #
I've had some time to think about Ambient Context since I had the (civil) discussion with Steven. The more I think about it, the more I think that he's right; that Ambient Context really is an anti-pattern.
I never use that pattern myself, so it's clear to me that for all the situations that I typically encounter, there's always better solutions, with no significant trade-offs.
The question is: could there be some niche scenario that I'm not aware of, where Ambient Context is a bona fide good solution?
The more I think about this, the more I'm beginning to believe that there isn't. It remains to be seen, though. It remains to be falsified.
Summary #
I'm so happy that Steven van Deursen agreed to co-author the second edition of Dependency Injection in .NET with me. The few areas where we've disagreed, I've ultimately come around to agree with him. He's truly taken a good book and made it better.
One of the changes is that Ambient Context is now classified as an anti-pattern. Originally, I wasn't sure that this was the correct thing to do, but I've since changed my mind. I do think that Ambient Context belongs in the anti-patterns chapter.
I could be wrong, though. I was before.
Comments
Thanks for great input for discussion :P
Like with all other patterns and anti-patterns, I think there's a time and a place.
Simply looking at it in a one-dimensional manner, i.e. asking "does there exist a solution to this problem with the same advantages but less downsides?" must be qualified with "IN THIS TIME AND PLACE", in my opinion.
This way, the patterns/anti-patterns distinction does not make that much sense in a global perspective, because all patterns can be an anti-patterns in some situations, and vice versa.
For example, I like what Ambient Context does in Rebus: It provides a mechanism that enables user code to transparently enlist its bus operations in a unit of work, without requiring user code to pass that unit of work to each operation.
This is very handy, e.g. in OWIN-based applications, where the unit of work can be managed by an OWIN middleware that uses a
RebusTransactionScope,
this way enlisting all send/publish operations on the bus in that unit of work.
Had it not been possible to automatically pick up an ongoing ambient Rebus transaction context, one would probably need to pollute the interfaces of one's application with an ITransactionContext argument,
thus not handling the cross-cutting concern of managing the unit of work in a cross-cutting manner.
Mogens, thank you for writing. The reason I explicitly framed my treatment in a discourse related to Pareto efficiency is exactly because this view on optima is multi-dimensional. When considering whether a 'solution coordinate' is Pareto-optimal or not, the question is exactly whether or not it's possible to improve at least one dimension without exacerbating any other dimension. If you can make one dimension better without trade-offs, then you can make a Pareto improvement. If you can only make one dimension better at the cost of one or more other dimensions, then you already have a Pareto-optimal solution.
The theory of Pareto efficiency doesn't say anything about the number of dimensions. Usually, as in the linked Wikipedia article, the concept is illustrated in the plane, but conceptually, it applies to an arbitrary number of dimensions.
In the context of anti-patterns, those dimensions include time and place, as you say.
I consider something to be an anti-pattern if I can make a change that constitutes an improvement in at least one dimension, without trading off of any other dimensions. In other words, in this article, I'm very deliberately not looking at it in a one-dimensional manner.
As I wrote, I'm still not sure that Ambient Context is an anti-pattern (although I increasingly believe it to be). How can we even test that hypothesis when we can't really quantify software design?
On the other hand, if we leave the question about Ambient Context for a moment, I feel confident that Service Locator is an anti-pattern, even in what you call a global perspective. The reason I believe that is that I made that falsifiable claim in 2010, and here, almost nine years later, no-one has successfully produced a valid counter-example.
I don't have the same long history with the claim about Ambient Context, so I could be wrong. Perhaps you are, right now, proving me wrong. I can't tell, though, because I don't (yet) know enough about Rebus to be able to tell whether what you describe is Pareto-optimal.
The question isn't whether the current design is 'handy'. The question is whether it's possible to come up with a design that's 'globally' better; i.e. either has all the advantages of the current design, but fewer disadvantages; or has more advantages, and only the same disadvantages.
I may be able to suggest such an improvement if provided with some code examples, but in the end we may never agree whether one design is better than another. After all, since we can't quantify software design, a subjective judgement will always remain.
Mark,
Thanks for this thoughtful meta-analysis of what it means to be an anti-pattern and how we think about them. What are some considerations when designing a replacement for ambient context objects? What patterns have you found succesful in object-oriented code? I'm sure you'd mention Constructor Injection and CQRS with decorators.
How might one refactor ambient context out of a solution? Some say passing around an object, maybe some sort of continuation?
Drew, thank you for writing. Indeed, in object-oriented code, I'd typically replace Ambient Contexts with either injected dependencies or Decorators. I'm not sure I see how CQRS fits into this picture.
When refactoring away an Ambient Context, it's typically, before the refactoring, used like Context.DoSomething(). The first step is often to inject a dependency and make it available to the class as a property called Context. IIRC, the C# overload resolution system should then pick the instance property over the static class, so that Context.DoSomething() calls DoSomething on the injected Context property.
There may be some static member that also use the Ambient Context. If that's the case, you'll first have to make those static members instance members.
Once you've made those replacements everywhere, you should be able to delete the Ambient Context.
An Either functor
Either forms a normal functor. A placeholder article for object-oriented programmers.
This article is an instalment in an article series about functors. As another article explains, Either is a bifunctor. This makes it trivially a functor. As such, this article is mostly a place-holder to fit the spot in the functor table of contents, thereby indicating that Either is a functor.
Since Either is a bifunctor, it's actually not one, but two, functors. Many languages, C# included, are best equipped to deal with unambiguous functors. This is also true in Haskell, where Either l r is only a Functor over the right side. Likewise, in C#, you can make IEither<L, R> a functor by implementing Select:
public static IEither<L, R1> Select<L, R, R1>( this IEither<L, R> source, Func<R, R1> selector) { return source.SelectRight(selector); }
This method simply delegates all implementation to the SelectRight method; it's just SelectRight by another name. It obeys the functor laws, since these are just specializations of the bifunctor laws, and we know that Either is a proper bifunctor.
It would have been technically possible to instead implement a Select method by calling SelectLeft, but it seems generally more useful to enable syntactic sugar for mapping over 'happy path' scenarios. This enables you to write projections over operations that can fail.
Here's some C# Interactive examples that use the FindWinner helper method from the Church-encoded Either article. Imagine that you're collecting votes; you're trying to pick the highest-voted integer, but in reality, you're only interested in seeing if the number is positive or not. Since FindWinner returns IEither<VoteError, T>, and this type is a functor, you can project the right result, while any left result short-circuits the query. First, here's a successful query:
> from i in FindWinner(1, 2, -3, -1, 2, -1, -1) select i > 0 Right<VoteError, bool>(false)
This query succeeds, resulting in a Right object. The contained value is false because the winner of the vote is -1, which isn't a positive number.
On the other hand, the following query fails because of a tie.
> from i in FindWinner(1, 2, -3, -1, 2, -1) select i > 0 Left<VoteError, bool>(Tie)
Because the result is tied on -1, the return value is a Left object containing the VoteError value Tie.
Another source of error is an empty input collection:
> from i in FindWinner<int>() select i > 0 Left<VoteError, bool>(Empty)
This time, the Left object contains the Empty error value, since no winner can be found from an empty collection.
While the Select method doesn't implement any behaviour that SelectRight doesn't already afford, it enables you to use C# query syntax, as demonstrated by the above examples.
Next: A Tree functor.
Either bifunctor
Either forms a bifunctor. An article for object-oriented programmers.
This article is an instalment in an article series about bifunctors. As the overview article explains, essentially there's two practically useful bifunctors: pairs and Either. In the previous article, you saw how a pair (a two-tuple) forms a bifunctor. In this article, you'll see how Either also forms a bifunctor.
Mapping both dimensions #
In the previous article, you saw how, if you have maps over both dimensions, you can trivially implement SelectBoth (what Haskell calls bimap):
return source.SelectFirst(selector1).SelectSecond(selector2);
The relationship can, however, go both ways. If you implement SelectBoth, you can derive SelectFirst and SelectSecond from it. In this article, you'll see how to do that for Either.
Given the Church-encoded Either, the implementation of SelectBoth can be achieved in a single expression:
public static IEither<L1, R1> SelectBoth<L, L1, R, R1>( this IEither<L, R> source, Func<L, L1> selectLeft, Func<R, R1> selectRight) { return source.Match<IEither<L1, R1>>( onLeft: l => new Left<L1, R1>( selectLeft(l)), onRight: r => new Right<L1, R1>(selectRight(r))); }
Given that the input source is an IEither<L, R> object, there's isn't much you can do. That interface only defines a single member, Match, so that's the only method you can call. When you do that, you have to supply the two arguments onLeft and onRight.
The Match method is defined like this:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight)
Given the desired return type of SelectBoth, you know that T should be IEither<L1, R1>. This means, then, that for onLeft, you must supply a function of the type Func<L, IEither<L1, R1>>. Since a functor is a structure-preserving map, you should translate a left case to a left case, and a right case to a right case. This implies that the concrete return type that matches IEither<L1, R1> for the onLeft argument is Left<L1, R1>.
When you write the function with the type Func<L, IEither<L1, R1>> as a lambda expression, the input argument l has the type L. In order to create a new Left<L1, R1>, however, you need an L1 object. How do you produce an L1 object from an L object? You call selectLeft with l, because selectLeft is a function of the type Func<L, L1>.
You can apply the same line of reasoning to the onRight argument. Write a lambda expression that takes an R object r as input, call selectRight to turn that into an R1 object, and return it wrapped in a new Right<L1, R1> object.
This works as expected:
> new Left<string, int>("foo").SelectBoth(string.IsNullOrWhiteSpace, i => new DateTime(i)) Left<bool, DateTime>(false) > new Right<string, int>(1337).SelectBoth(string.IsNullOrWhiteSpace, i => new DateTime(i)) Right<bool, DateTime>([01.01.0001 00:00:00])
Notice that both of the above statements evaluated in C# Interactive use the same projections as input to SelectBoth. Clearly, though, because the inputs are first a Left value, and secondly a Right value, the outputs differ.
Mapping the left side #
When you have SelectBoth, you can trivially implement the translations for each dimension in isolation. In the previous article, I called these methods SelectFirst and SelectSecond. In this article, I've chosen to instead name them SelectLeft and SelectRight, but they still corresponds to Haskell's first and second Bifunctor functions.
public static IEither<L1, R> SelectLeft<L, L1, R>(this IEither<L, R> source, Func<L, L1> selector) { return source.SelectBoth(selector, r => r); }
The method body is literally a one-liner. Just call SelectBoth with selector as the projection for the left side, and the identity function as the projection for the right side. This ensures that if the actual value is a Right<L, R> object, nothing's going to happen. Only if the input is a Left<L, R> object will the projection run:
> new Left<string, int>("").SelectLeft(string.IsNullOrWhiteSpace) Left<bool, int>(true) > new Left<string, int>("bar").SelectLeft(string.IsNullOrWhiteSpace) Left<bool, int>(false) > new Right<string, int>(42).SelectLeft(string.IsNullOrWhiteSpace) Right<bool, int>(42)
In the above C# Interactive session, you can see how projecting three different objects using string.IsNullOrWhiteSpace works. When the Left object indeed does contain an empty string, the result is a Left value containing true. When the object contains "bar", however, it contains false. Furthermore, when the object is a Right value, the mapping has no effect.
Mapping the right side #
Similar to SelectLeft, you can also trivially implement SelectRight:
public static IEither<L, R1> SelectRight<L, R, R1>(this IEither<L, R> source, Func<R, R1> selector) { return source.SelectBoth(l => l, selector); }
This is another one-liner calling SelectBoth, with the difference that the identity function l => l is passed as the first argument, instead of as the last. This ensures that only Right values are mapped:
> new Left<string, int>("baz").SelectRight(i => new DateTime(i)) Left<string, DateTime>("baz") > new Right<string, int>(1_234_567_890).SelectRight(i => new DateTime(i)) Right<string, DateTime>([01.01.0001 00:02:03])
In the above examples, Right integers are projected into DateTime values, whereas Left strings stay strings.
Identity laws #
Either obeys all the bifunctor laws. While it's formal work to prove that this is the case, you can get an intuition for it via examples. Often, I use a property-based testing library like FsCheck or Hedgehog to demonstrate (not prove) that laws hold, but in this article, I'll keep it simple and only cover each law with a parametrised test.
private static T Id<T>(T x) => x; public static IEnumerable<object[]> BifunctorLawsData { get { yield return new[] { new Left<string, int>("foo") }; yield return new[] { new Left<string, int>("bar") }; yield return new[] { new Left<string, int>("baz") }; yield return new[] { new Right<string, int>( 42) }; yield return new[] { new Right<string, int>( 1337) }; yield return new[] { new Right<string, int>( 0) }; } } [Theory, MemberData(nameof(BifunctorLawsData))] public void SelectLeftObeysFirstFunctorLaw(IEither<string, int> e) { Assert.Equal(e, e.SelectLeft(Id)); }
This test uses xUnit.net's [Theory] feature to supply a small set of example input values. The input values are defined by the BifunctorLawsData property, since I'll reuse the same values for all the bifunctor law demonstration tests.
The tests also use the identity function implemented as a private function called Id, since C# doesn't come equipped with such a function in the Base Class Library.
For all the IEither<string, int> objects e, the test simply verifies that the original Either e is equal to the Either projected over the first axis with the Id function.
Likewise, the first functor law applies when translating over the second dimension:
[Theory, MemberData(nameof(BifunctorLawsData))] public void SelectRightObeysFirstFunctorLaw(IEither<string, int> e) { Assert.Equal(e, e.SelectRight(Id)); }
This is the same test as the previous test, with the only exception that it calls SelectRight instead of SelectLeft.
Both SelectLeft and SelectRight are implemented by SelectBoth, so the real test is whether this method obeys the identity law:
[Theory, MemberData(nameof(BifunctorLawsData))] public void SelectBothObeysIdentityLaw(IEither<string, int> e) { Assert.Equal(e, e.SelectBoth(Id, Id)); }
Projecting over both dimensions with the identity function does, indeed, return an object equal to the input object.
Consistency law #
In general, it shouldn't matter whether you map with SelectBoth or a combination of SelectLeft and SelectRight:
[Theory, MemberData(nameof(BifunctorLawsData))] public void ConsistencyLawHolds(IEither<string, int> e) { bool f(string s) => string.IsNullOrWhiteSpace(s); DateTime g(int i) => new DateTime(i); Assert.Equal(e.SelectBoth(f, g), e.SelectRight(g).SelectLeft(f)); Assert.Equal( e.SelectLeft(f).SelectRight(g), e.SelectRight(g).SelectLeft(f)); }
This example creates two local functions f and g. The first function, f, just delegates to string.IsNullOrWhiteSpace, although I want to stress that this is just an example. The law should hold for any two (pure) functions. The second function, g, creates a new DateTime object from an integer, using one of the DateTime constructor overloads.
The test then verifies that you get the same result from calling SelectBoth as when you call SelectLeft followed by SelectRight, or the other way around.
Composition laws #
The composition laws insist that you can compose functions, or translations, and that again, the choice to do one or the other doesn't matter. Along each of the axes, it's just the second functor law applied. This parametrised test demonstrates that the law holds for SelectLeft:
[Theory, MemberData(nameof(BifunctorLawsData))] public void SecondFunctorLawHoldsForSelectLeft(IEither<string, int> e) { bool f(int x) => x % 2 == 0; int g(string s) => s.Length; Assert.Equal(e.SelectLeft(x => f(g(x))), e.SelectLeft(g).SelectLeft(f)); }
Here, f is the even function, whereas g is a local function that returns the length of a string. The second functor law states that mapping f(g(x)) in a single step is equivalent to first mapping over g and then map the result of that using f.
The same law applies if you fix the first dimension and translate over the second:
[Theory, MemberData(nameof(BifunctorLawsData))] public void SecondFunctorLawHoldsForSelectRight(IEither<string, int> e) { char f(bool b) => b ? 'T' : 'F'; bool g(int i) => i % 2 == 0; Assert.Equal(e.SelectRight(x => f(g(x))), e.SelectRight(g).SelectRight(f)); }
Here, f is a local function that returns 'T' for true and 'F' for false, and g is a local function that, as you've seen before, determines whether a number is even. Again, the test demonstrates that the output is the same whether you map over an intermediary step, or whether you map using only a single step.
This generalises to the composition law for SelectBoth:
[Theory, MemberData(nameof(BifunctorLawsData))] public void SelectBothCompositionLawHolds(IEither<string, int> e) { bool f(int x) => x % 2 == 0; int g(string s) => s.Length; char h(bool b) => b ? 'T' : 'F'; bool i(int x) => x % 2 == 0; Assert.Equal( e.SelectBoth(x => f(g(x)), y => h(i(y))), e.SelectBoth(g, i).SelectBoth(f, h)); }
Again, whether you translate in one or two steps shouldn't affect the outcome.
As all of these tests demonstrate, the bifunctor laws hold for Either. The tests only showcase six examples for either a string or an integer, but I hope it gives you an intuition how any Either object is a bifunctor. After all, the SelectLeft, SelectRight, and SelectBoth methods are all generic, and they behave the same for all generic type arguments.
Summary #
Either objects are bifunctors. You can translate the first and second dimension of an Either object independently of each other, and the bifunctor laws hold for any pure translation, no matter how you compose the projections.
As always, there can be performance differences between the various compositions, but the outputs will be the same regardless of composition.
A functor, and by extension, a bifunctor, is a structure-preserving map. This means that any projection preserves the structure of the underlying container. For Either objects, it means that left objects remain left objects, and right objects remain right objects, even if the contained values change. Either is characterised by containing exactly one value, but it can be either a left value or a right value. No matter how you translate it, it still contains only a single value - left or right.
The other common bifunctor, pair, is complementary. Not only does it also have two dimensions, but a pair always contains both values at once.
Next: Rose tree bifunctor.
Comments
I feel like the concepts of functor and bifunctor were used somewhat interchangeably in this post. Can we clarify this relationship?
To help us with this, consider type variance. The generic type Func<A> is covariant, but more specifically, it is covariant on A. That additional prepositional phrase is often omitted because it can be inferred. In contrast, the generic type Func<A, B> is both covariant and contravariant but (of course) not on the same type parameter. It is covariant in B and contravariant in A.
I feel like saying that a generic type with two type parameters is a (bi)functor also needs an additional prepositional phrase. Like, Either<L, R> is a bifunctor in L and R, so it is also a functor in L and a functor in R.
Does this seem like a clearer way to talk about a specific type being both a bifunctor and a fuctor?
Tyson, thank you for writing. I find no fault with what you wrote. Is it clearer? I don't know.
One thing that's surprised me throughout this endeavour is exactly what does or doesn't confuse readers. This, I can't predict.
A functor is, by its definition, assumed to be covariant. Contravariant functors also exist, but they're explicitly named contravariant functors to distinguish them from standard functors.
Ultimately, co- or contravariance of generic type arguments is (I think) insufficient to identify a type as a functor. Whether or not something is a functor is determined by whether or not it obeys the functor laws. Can we guarantee that all types with a covariant type argument will obey the functor laws?
I wasn't trying to discuss the relationship between functors and type variance. I just brought up type variance as an example in programming where I think adding additional prepositional phrases to statements can clarify things.

Comments
Hi Mark,
I think I came to the same conclusion (maybe not the same solution), meaning you can't write solid tests when mocking all the dependencies interaction : all these dependencies interaction are implementation details (even the database system you chose). For writing solid tests I chose to write my tests like this : start all the services I can in test environment (database, queue ...), mock only things I have no choice (external PSP or Google Captcha), issue command (using MediatR) and check the result with a query. You can find some of my work here . The work is not done on all the tests but this is the way I want to go. Let me know what you think about it.
I could have launched the tests at the Controller level but I chose Command and Query handler.
Can't wait to see your solution
Rémi, thank you for writing. Hosting services as part of a test run can be a valuable addition to an overall testing or release pipeline. It's reminiscent of the approach taken in GOOS. I've also touched on this option in my Pluralsight course Outside-In Test-Driven Development. This is, however, a set of tests I would identify as belonging towards the top of a Test Pyramid. In my experience, such tests tend to run (an order of magnitude) slower than unit tests.
That doesn't preclude their use. Depending on circumstances, I still prefer having tests like that. I think that I've written a few applications where tests like that constituted the main body of unit tests.
I do, however, also find this style of testing too limiting in many situation. I tend to prefer 'real' unit tests, since they tend to be easier to write, and they execute faster.
Apart from performance and maintainability concerns, one problem that I often see with integration tests is that it's practically impossible to cover all edge cases. This tends to lead to either bug-ridden software, or unmaintainable test suites.
Still, I think that, ultimately, having enough experience with different styles of testing enables one to make an informed choice. That's my purpose with these articles: to point out that alternatives exist.