ploeh blog danish software design
Endomorphic Composite as a monoid
A variation of the Composite design pattern uses endomorphic composition. That's still a monoid.
This article is part of a series of articles about design patterns and their category theory counterparts. In a previous article, you learned that the Composite design pattern is simply a monoid.
There is, however, a variation of the Composite design pattern where the return value from one step can be used as the input for the next step.
Endomorphic API #
Imagine that you have to implement some scheduling functionality. For example, you may need to schedule something to happen a month from now, but it should happen on a bank day, during business hours, and you want to know what the resulting date and time will be, expressed in UTC. I've previously covered the various objects for performing such steps. The common behaviour is this interface:
public interface IDateTimeOffsetAdjustment { DateTimeOffset Adjust(DateTimeOffset value); }
The Adjust method is an endomorphism; that is: the input type is the same as the return type, in this case DateTimeOffset. A previous article already established that that's a monoid.
Composite endomorphism #
If you have various implementations of IDateTimeOffsetAdjustment, you can make a Composite from them, like this:
public class CompositeDateTimeOffsetAdjustment : IDateTimeOffsetAdjustment { private readonly IReadOnlyCollection<IDateTimeOffsetAdjustment> adjustments; public CompositeDateTimeOffsetAdjustment( IReadOnlyCollection<IDateTimeOffsetAdjustment> adjustments) { if (adjustments == null) throw new ArgumentNullException(nameof(adjustments)); this.adjustments = adjustments; } public DateTimeOffset Adjust(DateTimeOffset value) { var acc = value; foreach (var adjustment in this.adjustments) acc = adjustment.Adjust(acc); return acc; } }
The Adjust method simply starts with the input value and loops over all the composed adjustments. For each adjustment it adjusts acc to produce a new acc value. This goes on until all adjustments have had a chance to adjust the value.
Notice that if adjustments is empty, the Adjust method simply returns the input value. In that degenerate case, the behaviour is similar to the identity function, which is the identity for the endomorphism monoid.
You can now compose the desired behaviour, as this parametrised xUnit.net test demonstrates:
[Theory] [InlineData("2017-01-31T07:45:55+2", "2017-02-28T07:00:00Z")] [InlineData("2017-02-06T10:03:02+1", "2017-03-06T09:03:02Z")] [InlineData("2017-02-09T04:20:00Z" , "2017-03-09T09:00:00Z")] [InlineData("2017-02-12T16:02:11Z" , "2017-03-10T16:02:11Z")] [InlineData("2017-03-14T13:48:29-1", "2017-04-13T14:48:29Z")] public void AdjustReturnsCorrectResult( string dtS, string expectedS) { var dt = DateTimeOffset.Parse(dtS); var sut = new CompositeDateTimeOffsetAdjustment( new NextMonthAdjustment(), new BusinessHoursAdjustment(), new DutchBankDayAdjustment(), new UtcAdjustment()); var actual = sut.Adjust(dt); Assert.Equal(DateTimeOffset.Parse(expectedS), actual); }
You can see the implementation for all four composed classes in the previous article. NextMonthAdjustment adjusts a date by a month into its future, BusinessHoursAdjustment adjusts a time to business hours, DutchBankDayAdjustment takes bank holidays and weekends into account in order to return a bank day, and UtcAdjustment convert a date and time to UTC.
Monoidal accumulation #
As you've learned in that previous article that I've already referred to, an endomorphism is a monoid. In this particular example, the binary operation in question is called Append. From another article, you know that monoids accumulate:
public static IDateTimeOffsetAdjustment Accumulate( IReadOnlyCollection<IDateTimeOffsetAdjustment> adjustments) { IDateTimeOffsetAdjustment acc = new IdentityDateTimeOffsetAdjustment(); foreach (var adjustment in adjustments) acc = Append(acc, adjustment); return acc; }
This implementation follows the template previously described:
- Initialize a variable
accwith the identity element. In this case, the identity is a class calledIdentityDateTimeOffsetAdjustment. - For each
adjustmentinadjustments,Appendtheadjustmenttoacc. - Return
acc.
mconcat. We'll get back to that in a moment, but first, here's another parametrised unit test that exercises the same test cases as the previous test, only against a composition created by Accumulate:
[Theory] [InlineData("2017-01-31T07:45:55+2", "2017-02-28T07:00:00Z")] [InlineData("2017-02-06T10:03:02+1", "2017-03-06T09:03:02Z")] [InlineData("2017-02-09T04:20:00Z" , "2017-03-09T09:00:00Z")] [InlineData("2017-02-12T16:02:11Z" , "2017-03-10T16:02:11Z")] [InlineData("2017-03-14T13:48:29-1", "2017-04-13T14:48:29Z")] public void AccumulatedAdjustReturnsCorrectResult( string dtS, string expectedS) { var dt = DateTimeOffset.Parse(dtS); var sut = DateTimeOffsetAdjustment.Accumulate( new NextMonthAdjustment(), new BusinessHoursAdjustment(), new DutchBankDayAdjustment(), new UtcAdjustment()); var actual = sut.Adjust(dt); Assert.Equal(DateTimeOffset.Parse(expectedS), actual); }
While the implementation is different, this monoidal composition has the same behaviour as the above CompositeDateTimeOffsetAdjustment class. This, again, emphasises that Composites are simply monoids.
Endo #
For comparison, this section demonstrates how to implement the above behaviour in Haskell. The code here passes the same test cases as those above. You can skip to the next section if you want to get to the conclusion.
Instead of classes that implement interfaces, in Haskell you can define functions with the type ZonedTime -> ZonedTime. You can compose such functions using the Endo newtype 'wrapper' that turns endomorphisms into monoids:
λ> adjustments = reverse [adjustToNextMonth, adjustToBusinessHours, adjustToDutchBankDay, adjustToUtc] λ> :type adjustments adjustments :: [ZonedTime -> ZonedTime] λ> adjust = appEndo $ mconcat $ Endo <$> adjustments λ> :type adjust adjust :: ZonedTime -> ZonedTime
In this example, I'm using GHCi (the Haskell REPL) to show the composition in two steps. The first step creates adjustments, which is a list of functions. In case you're wondering about the use of the reverse function, it turns out that mconcat composes from right to left, which I found counter-intuitive in this case. adjustToNextMonth should execute first, followed by adjustToBusinessHours, and so on. Defining the functions in the more intuitive left-to-right direction and then reversing it makes the code easier to understand, I hope.
(For the Haskell connoisseurs, you can also achieve the same result by composing Endo with the Dual monoid, instead of reversing the list of adjustments.)
The second step composes adjust from adjustments. It first maps adjustments to Endo values. While ZonedTime -> ZonedTime isn't a Monoid instances, Endo ZonedTime is. This means that you can reduce a list of Endo ZonedTime with mconcat. The result is a single Endo ZonedTime value, which you can then unwrap to a function using appEndo.
adjust is a function that you can call:
λ> dt 2017-01-31 07:45:55 +0200 λ> adjust dt 2017-02-28 07:00:00 +0000
In this example, I'd already prepared a ZonedTime value called dt. Calling adjust returns a new ZonedTime adjusted by all four composed functions.
Conclusion #
In general, you implement the Composite design pattern by calling all composed functions with the original input value, collecting the return value of each call. In the final step, you then reduce the collected return values to a single value that you return. This requires the return type to form a monoid, because otherwise, you can't reduce it.
In this article, however, you learned about an alternative implementation of the Composite design pattern. If the method that you compose has the same output type as its input, you can pass the output from one object as the input to the next object. In that case, you can escape the requirement that the return value is a monoid. That's the case with DateTimeOffset and ZonedTime: neither are monoids, because you can't add two dates and times together.
At first glance, then, it seems like a falsification of the original claim that Composites are monoids. As you've learned in this article, however, endomorphisms are monoids, so the claim still stands.
Next: Null Object as identity.
Coalescing Composite as a monoid
A variation of the Composite design pattern uses coalescing behaviour to return non-composable values. That's still a monoid.
This article is part of a series of articles about design patterns and their category theory counterparts. In a previous article, you learned that the Composite design pattern is simply a monoid.
Monoidal return types #
When all methods of an interface return monoids, you can create a Composite. This is fairly intuitive once you understand what a monoid is. Consider this example interface:
public interface ICustomerRepository { void Create(Customer customer); Customer Read(Guid id); void Update(Customer customer); void Delete(Guid id); }
While this interface is, in fact, not readily composable, most of the methods are. It's easy to compose the three void methods. Here's a composition of the Create method:
public void Create(Customer customer) { foreach (var repository in this.repositories) repository.Create(customer); }
In this case it's easy to compose multiple repositories, because void (or, rather, unit) forms a monoid. If you have methods that return numbers, you can add the numbers together (a monoid). If you have methods that return strings, you can concatenate the strings (a monoid). If you have methods that return Boolean values, you can or or and them together (more monoids).
What about the above Read method, though?
Picking the first Repository #
Why would you even want to compose two repositories? One scenario is where you have an old data store, and you want to move to a new data store. For a while, you wish to write to both data stores, but one of them stays the 'primary' data store, so this is the one from which you read.
Imagine that the old repository saves customer information as JSON files on disk. The new data store, on the other hand, saves customer data as JSON documents in Azure Blob Storage. You've already written two implementations of ICustomerRepository: FileCustomerRepository and AzureCustomerRepository. How do you compose them?
The three methods that return void are easy, as the above Create implementation demonstrates. The Read method, however, is more tricky.
One option is to only query the first repository, and return its return value:
public Customer Read(Guid id) { return this.repositories.First().Read(id); }
This works, but doesn't generalise. It works if you know that you have a non-empty collection of repositories, but if you want to adhere to the Liskov Substitution Principle, you should be able to handle the case where there's no repositories.
A Composite should be able to compose an arbitrary number of other objects. This includes a collection of no objects. The CompositeCustomerRepository class has this constructor:
private readonly IReadOnlyCollection<ICustomerRepository> repositories; public CompositeCustomerRepository( IReadOnlyCollection<ICustomerRepository> repositories) { if (repositories == null) throw new ArgumentNullException(nameof(repositories)); this.repositories = repositories; }
It uses standard Constructor Injection to inject an IReadOnlyCollection<ICustomerRepository>. Such a collection is finite, but can be empty.
Another problem with blindly returning the value from the first repository is that the return value may be empty.
In C#, people often use null to indicate a missing value, and while I find such practice unwise, I'll pursue this option for a bit.
A more robust Composite would return the first non-null value it gets:
public Customer Read(Guid id) { foreach (var repository in this.repositories) { var customer = repository.Read(id); if (customer != null) return customer; } return null; }
This implementation loops through all the injected repositories and calls Read on each until it gets a result that is not null. This will often be the first value, but doesn't have to be. If all repositories return null, then the Composite also returns null. To emphasise my position, I would never design C# code like this, but at least it's consistent.
If you've ever worked with relational databases, you may have had an opportunity to use the COALESCE function, which works in exactly the same way. This is the reason I call such an implementation a coalescing Composite.
The First monoid #
The T-SQL documentation for COALESCE describes the operation like this:
"Evaluates the arguments in order and returns the current value of the first expression that initially does not evaluate to NULL."
The Oracle documentation expresses it as:
"This may not be apparent, but that's a monoid.COALESCEreturns the first non-nullexprin the expression list."
Haskell's base library comes with a monoidal type called First, which is a
"Maybe monoid returning the leftmost non-Nothing value."Sounds familiar?
Here's how you can use it in GHCi:
λ> First (Just (Customer id1 "Joan")) <> First (Just (Customer id2 "Nigel"))
First {getFirst = Just (Customer {customerId = 1243, customerName = "Joan"})}
λ> First (Just (Customer id1 "Joan")) <> First Nothing
First {getFirst = Just (Customer {customerId = 1243, customerName = "Joan"})}
λ> First Nothing <> First (Just (Customer id2 "Nigel"))
First {getFirst = Just (Customer {customerId = 5cd5, customerName = "Nigel"})}
λ> First Nothing <> First Nothing
First {getFirst = Nothing}
(To be clear, the above examples uses First from Data.Monoid, not First from Data.Semigroup.)
The operator <> is an infix alias for mappend - Haskell's polymorphic binary operation.
As long as the left-most value is present, that's the return value, regardless of whether the right value is Just or Nothing. Only when the left value is Nothing is the right value returned. Notice that this value may also be Nothing, causing the entire expression to be Nothing.
That's exactly the same behaviour as the above implementation of the Read method.
First in C# #
It's easy to port Haskell's First type to C#:
public class First<T> { private readonly T item; private readonly bool hasItem; public First() { this.hasItem = false; } public First(T item) { if (item == null) throw new ArgumentNullException(nameof(item)); this.item = item; this.hasItem = true; } public First<T> FindFirst(First<T> other) { if (this.hasItem) return this; else return other; } }
Instead of nesting Maybe inside of First, as Haskell does, I simplified a bit and gave First<T> two constructor overloads: one that takes a value, and one that doesn't. The FindFirst method is the binary operation that corresponds to Haskell's <> or mappend.
This is only one of several alternative implementations of the first monoid.
In order to make First<T> a monoid, it must also have an identity, which is just an empty value:
public static First<T> Identity<T>() { return new First<T>(); }
This enables you to accumulate an arbitrary number of First<T> values to a single value:
public static First<T> Accumulate<T>(IReadOnlyList<First<T>> firsts) { var acc = Identity<T>(); foreach (var first in firsts) acc = acc.FindFirst(first); return acc; }
You start with the identity, which is also the return value if firsts is empty. If that's not the case, you loop through all firsts and update acc by calling FindFirst.
A composable Repository #
You can formalise such a design by changing the ICustomerRepository interface:
public interface ICustomerRepository { void Create(Customer customer); First<Customer> Read(Guid id); void Update(Customer customer); void Delete(Guid id); }
In this modified version, Read explicitly returns First<Customer>. The rest of the methods remain as before.
The reusable API of First makes it easy to implement a Composite version of Read:
public First<Customer> Read(Guid id) { var candidates = new List<First<Customer>>(); foreach (var repository in this.repositories) candidates.Add(repository.Read(id)); return First.Accumulate(candidates); }
You could argue that this seems to be wasteful, because it calls Read on all repositories. If the first Repository returns a value, all remaining queries are wasted. You can address that issue with lazy evaluation.
You can see (a recording of) a live demo of the example in this article in my Clean Coders video Composite as Universal Abstraction.
Summary #
While the typical Composite is implemented by directly aggregating the return values from the composed objects, variations exist. One variation picks the first non-empty value from a collection of candidates, reminiscent of the SQL COALESCE function. This is, however, still a monoid, so the overall conjecture that Composites are monoids still holds.
Another Composite variation exists, but that one turns out to be a monoid as well. Read on!
Maybe monoids
You can combine Maybe objects in several ways. An article for object-oriented programmers.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
You can combine Maybe objects in various ways, thereby turning them into monoids. There's at least two unconstrained monoids over Maybe values, as well as some constrained monoids. By constrained I mean that the monoid only exists for Maybe objects that contain certain values. You'll see such an example first.
Combining Maybes over semigroups #
If you have two Maybe objects, and they both (potentially) contain values that form a semigroup, you can combine the Maybe values as well. Here's a few examples.
public static Maybe<int> CombineMinimum(Maybe<int> x, Maybe<int> y) { if (x.HasItem && y.HasItem) return new Maybe<int>(Math.Min(x.Item, y.Item)); if (x.HasItem) return x; return y; }
In this first example, the semigroup operation in question is the minimum operation. Since C# doesn't enable you to write generic code over mathematical operations, the above method just gives you an example implemented for Maybe<int> values. If you also want to support e.g. Maybe<decimal> or Maybe<long>, you'll have to add overloads for those types.
If both x and y have values, you get the minimum of those, still wrapped in a Maybe container:
var x = new Maybe<int>(42); var y = new Maybe<int>(1337); var m = Maybe.CombineMinimum(x, y);
Here, m is a new Maybe<int>(42).
It's possible to combine any two Maybe objects as long as you have a way to combine the contained values in the case where both Maybe objects contain values. In other words, you need a binary operation, so the contained values must form a semigroup, like, for example, the minimum operation. Another example is maximum:
public static Maybe<decimal> CombineMaximum(Maybe<decimal> x, Maybe<decimal> y) { if (x.HasItem && y.HasItem) return new Maybe<decimal>(Math.Max(x.Item, y.Item)); if (x.HasItem) return x; return y; }
In order to vary the examples, I chose to implement this operation for decimal instead of int, but you can see that the implementation code follows the same template. When both x and y contains values, you invoke the binary operation. If, on the other hand, y is empty, then right identity still holds:
var x = new Maybe<decimal>(42); var y = new Maybe<decimal>(); var m = Maybe.CombineMaximum(x, y);
Since y in the above example is empty, the resulting object m is a new Maybe<decimal>(42).
You don't have to constrain yourself to semigroups exclusively. You can use a monoid as well, such as the sum monoid:
public static Maybe<long> CombineSum(Maybe<long> x, Maybe<long> y) { if (x.HasItem && y.HasItem) return new Maybe<long>(x.Item + y.Item); if (x.HasItem) return x; return y; }
Again, notice how most of this code is boilerplate code that follows the same template as above. In C#, unfortunately, you have to write out all the combinations of operations and contained types, but in Haskell, with its stronger type system, it all comes in the base library:
Prelude Data.Semigroup> Option (Just (Min 42)) <> Option (Just (Min 1337))
Option {getOption = Just (Min {getMin = 42})}
Prelude Data.Semigroup> Option (Just (Max 42)) <> mempty
Option {getOption = Just (Max {getMax = 42})}
Prelude Data.Semigroup> mempty <> Option (Just (Sum 1337))
Option {getOption = Just (Sum {getSum = 1337})}
That particular monoid over Maybe, however, does require as a minimum that the contained values form a semigroup. There are other monoids over Maybe that don't have any such constraints.
First #
As you can read in the introductory article about semigroups, there's two semigroup operations called first and last. Similarly, there's two operations by the same name defined over monoids. They behave a little differently, although they're related.
The first monoid operation returns the left-most non-empty value among candidates. You can view nothing as being a type-safe equivalent to null, in which case this monoid is equivalent to a null coalescing operator.
public static Maybe<T> First<T>(Maybe<T> x, Maybe<T> y) { if (x.HasItem) return x; return y; }
As long as x contains a value, First returns it. The contained values don't have to form monoids or semigroups, as this example demonstrates:
var x = new Maybe<Guid>(new Guid("03C2ECDBEF1D46039DE94A9994BA3C1E")); var y = new Maybe<Guid>(new Guid("A1B7BC82928F4DA892D72567548A8826")); var m = Maybe.First(x, y);
While I'm not aware of any reasonable way to combine GUIDs, you can still pick the left-most non-empty value. In the above example, m contains 03C2ECDBEF1D46039DE94A9994BA3C1E. If, on the other hand, the first value is empty, you get a different result:
var x = new Maybe<Guid>(); var y = new Maybe<Guid>(new Guid("2A2D19DE89D84EFD9E5BEE7C4ADAFD90")); var m = Maybe.First(x, y);
In this case, m contains 2A2D19DE89D84EFD9E5BEE7C4ADAFD90, even though it comes from y.
Notice that there's no guarantee that First returns a non-empty value. If both x and y are empty, then the result is also empty. The First operation is an associative binary operation, and the identity is the empty value (often called nothing or none). It's a monoid.
Last #
Since you can define a binary operation called First, it's obvious that you can also define one called Last:
public static Maybe<T> Last<T>(Maybe<T> x, Maybe<T> y) { if (y.HasItem) return y; return x; }
This operation returns the right-most non-empty value:
var x = new Maybe<Guid>(new Guid("1D9326CDA0B3484AB495DFD280F990A3")); var y = new Maybe<Guid>(new Guid("FFFC6CE263C7490EA0290017FE02D9D4")); var m = Maybe.Last(x, y);
In this example, m contains FFFC6CE263C7490EA0290017FE02D9D4, but while Last favours y, it'll still return x if y is empty. Notice that, like First, there's no guarantee that you'll receive a populated Maybe. If both x and y are empty, the result will be empty as well.
Like First, Last is an associative binary operation with nothing as the identity.
Generalisation #
The first examples you saw in this article (CombineMinimum, CombineMaximum, and so on), came with the constraint that the contained values form a semigroup. The First and Last operations, on the other hand, seem unconstrained. They work even on GUIDs, which notoriously can't be combined.
If you recall, though, first and last are both associative binary operations. They are, in fact, unconstrained semigroups. Recall the Last semigroup:
public static T Last<T>(T x, T y) { return y; }
This binary operation operates on any unconstrained type T, including Guid. It unconditionally returns y.
You could implement the Last monoid over Maybe using the same template as above, utilising the underlying semigroup:
public static Maybe<T> Last<T>(Maybe<T> x, Maybe<T> y) { if (x.HasItem && y.HasItem) return new Maybe<T>(Last(x.Item, y.Item)); if (x.HasItem) return x; return y; }
This implementation has exactly the same behaviour as the previous implementation of Last shown earlier. You can implement First in the same way.
That's exactly how Haskell works:
Prelude Data.Semigroup Data.UUID.Types> x =
sequence $ Last $ fromString "03C2ECDB-EF1D-4603-9DE9-4A9994BA3C1E"
Prelude Data.Semigroup Data.UUID.Types> x
Just (Last {getLast = 03c2ecdb-ef1d-4603-9de9-4a9994ba3c1e})
Prelude Data.Semigroup Data.UUID.Types> y =
sequence $ Last $ fromString "A1B7BC82-928F-4DA8-92D7-2567548A8826"
Prelude Data.Semigroup Data.UUID.Types> y
Just (Last {getLast = a1b7bc82-928f-4da8-92d7-2567548a8826})
Prelude Data.Semigroup Data.UUID.Types> Option x <> Option y
Option {getOption = Just (Last {getLast = a1b7bc82-928f-4da8-92d7-2567548a8826})}
Prelude Data.Semigroup Data.UUID.Types> Option x <> mempty
Option {getOption = Just (Last {getLast = 03c2ecdb-ef1d-4603-9de9-4a9994ba3c1e})}
The <> operator is the generic binary operation, and the way Haskell works, it changes behaviour depending on the type upon which it operates. Option is a wrapper around Maybe, and Last represents the last semigroup. When you stack UUID values inside of Option Last, you get the behaviour of selecting the right-most non-empty value.
In fact,
Any semigroup S may be turned into a monoid simply by adjoining an element e not in S and defining e • s = s = s • e for all s ∈ S.
That's just a mathematical way of saying that if you have a semigroup, you can add an extra value e and make e behave like the identity for the monoid you're creating. That extra value is nothing. The way Haskell's Data.Semigroup module models a monoid over Maybe instances aligns with the underlying mathematics.
Conclusion #
Just as there's more than one monoid over numbers, and more than one monoid over Boolean values, there's more than one monoid over Maybe values. The most useful one may be the one that elevates any semigroup to a monoid by adding nothing as the identity, but others exist. While, at first glance, the first and last monoids over Maybes look like operations in their own right, they're just applications of the general rule. They elevate the first and last semigroups to monoids by 'wrapping' them in Maybes, and using nothing as the identity.
Next: Lazy monoids.
The Maybe functor
An introduction to the Maybe functor for object-oriented programmers.
This article is an instalment in an article series about functors.
One of the simplest, and easiest to understand, functors is Maybe. It's also sometimes known as the Maybe monad, but this is not a monad tutorial; it's a functor tutorial. Maybe is many things; one of them is a functor. In F#, Maybe is called option.
Motivation #
Maybe enables you to model a value that may or may not be present. Object-oriented programmers typically have a hard time grasping the significance of Maybe, since it essentially does the same as null in mainstream object-oriented languages. There are differences, however. In languages like C# and Java, most things can be null, which can lead to much defensive coding. What happens more frequently, though, is that programmers forget to check for null, with run-time exceptions as the result.
A Maybe value, on the other hand, makes it explicit that a value may or may not be present. In statically typed languages, it also forces you to deal with the case where no data is present; if you don't, your code will not compile.
Finally, in a language like C#, null has no type, but a Maybe value always has a type.
If you appreciate the tenet that explicit is better than implicit, then you should favour Maybe over null.
Implementation #
If you've read the introduction, then you know that IEnumerable<T> is a functor. In many ways, Maybe is like IEnumerable<T>, but it's a particular type of collection that can only contain zero or one element(s). There are various ways in which you can implement Maybe in an object-oriented language like C#; here's one:
public sealed class Maybe<T> { internal bool HasItem { get; } internal T Item { get; } public Maybe() { this.HasItem = false; } public Maybe(T item) { if (item == null) throw new ArgumentNullException(nameof(item)); this.HasItem = true; this.Item = item; } public Maybe<TResult> Select<TResult>(Func<T, TResult> selector) { if (selector == null) throw new ArgumentNullException(nameof(selector)); if (this.HasItem) return new Maybe<TResult>(selector(this.Item)); else return new Maybe<TResult>(); } public T GetValueOrFallback(T fallbackValue) { if (fallbackValue == null) throw new ArgumentNullException(nameof(fallbackValue)); if (this.HasItem) return this.Item; else return fallbackValue; } public override bool Equals(object obj) { var other = obj as Maybe<T>; if (other == null) return false; return object.Equals(this.Item, other.Item); } public override int GetHashCode() { return this.HasItem ? this.Item.GetHashCode() : 0; } }
This is a generic class with two constructors. The parameterless constructor indicates the case where no value is present, whereas the other constructor overload indicates the case where exactly one value is available. Notice that a guard clause prevents you from accidentally passing null as a value.
The Select method has the correct signature for a functor. If a value is present, it uses the selector method argument to map item to a new value, and return a new Maybe<TResult> value. If no value is available, then a new empty Maybe<TResult> value is returned.
This class also override Equals. This isn't necessary in order for it to be a functor, but it makes it easier to compare two Maybe<T> values.
A common question about such generic containers is: how do you get the value out of the container?
The answer depends on the particular container, but in this example, I decided to enable that functionality with the GetValueOrFallback method. The only way to get the item out of a Maybe value is by supplying a fall-back value that can be used if no value is available. This is one way to guarantee that you, as a client developer, always remember to deal with the empty case.
Usage #
It's easy to use this Maybe class:
var source = new Maybe<int>(42);
This creates a new Maybe<int> object that contains the value 42. If you need to change the value inside the object, you can, for example, do this:
Maybe<string> dest = source.Select(x => x.ToString());
Since C# natively understands functors through its query syntax, you could also have written the above translation like this:
Maybe<string> dest = from x in source select x.ToString();
It's up to you and your collaborators whether you prefer one or the other of those alternatives. In both examples, though, dest is a new populated Maybe<string> object containing the string "42".
A more realistic example could be as part of a line-of-business application. Many enterprise developers are familiar with the Repository pattern. Imagine that you'd like to query a repository for a Reservation object. If one is found in the database, you'd like to convert it to a view model, so that you can display it.
var viewModel = repository.Read(id) .Select(r => r.ToViewModel()) .GetValueOrFallback(ReservationViewModel.Null);
The repository's Read method returns Maybe<Reservation>, indicating that it's possible that no object is returned. This will happen if you're querying the repository for an id that doesn't exist in the underlying database.
While you can translate the (potential) Reservation object to a view model (using the ToViewModel extension method), you'll have to supply a default view model to handle the case when the reservation wasn't found.
ReservationViewModel.Null is a static read-only class field implementing the Null Object pattern. Here, it's used for the fall-back value, in case no object was returned from the repository.
Notice that while you need a fall-back value at the end of your fluent interface pipeline, you don't need fall-back values for any intermediate steps. Specifically, you don't need a Null Object implementation for your domain model (Reservation). Furthermore, no defensive coding is required, because Maybe<T> guarantees that the object passed to selector is never null.
First functor law #
A Select method with the right signature isn't enough to be a functor. It must also obey the functor laws. Maybe obeys both laws, which you can demonstrate with a few examples. Here's some test cases for a populated Maybe:
[Theory] [InlineData("")] [InlineData("foo")] [InlineData("bar")] [InlineData("corge")] [InlineData("antidisestablishmentarianism")] public void PopulatedMaybeObeysFirstFunctorLaw(string value) { Func<string, string> id = x => x; var m = new Maybe<string>(value); Assert.Equal(m, m.Select(id)); }
This parametrised unit test uses xUnit.net to demonstrate that a populated Maybe value doesn't change when translated with the local id function, since id returns the input unchanged.
The first functor law holds for an empty Maybe as well:
[Fact] public void EmptyMaybeObeysFirstFunctorLaw() { Func<string, string> id = x => x; var m = new Maybe<string>(); Assert.Equal(m, m.Select(id)); }
When a Maybe starts empty, translating it with id doesn't change that it's empty. It's worth noting, however, that the original and the translated objects are considered equal because Maybe<T> overrides Equals. Even in the case of the empty Maybe, the value returned by Select(id) is a new object, with a memory address different from the original value.
Second functor law #
You can also demonstrate the second functor law with some examples, starting with some test cases for the populated case:
[Theory] [InlineData("", true)] [InlineData("foo", false)] [InlineData("bar", false)] [InlineData("corge", false)] [InlineData("antidisestablishmentarianism", true)] public void PopulatedMaybeObeysSecondFunctorLaw(string value, bool expected) { Func<string, int> g = s => s.Length; Func<int, bool> f = i => i % 2 == 0; var m = new Maybe<string>(value); Assert.Equal(m.Select(g).Select(f), m.Select(s => f(g(s)))); }
In this parametrised test, f and g are two local functions. g returns the length of a string (for example, the length of antidisestablishmentarianism is 28). f evaluates whether or not a number is even.
Whether you decide to first translate m with g, and then translate the return value with f, or you decide to translate the composition of those functions in a single Select method call, the result should be the same.
The second functor law holds for the empty case as well:
[Fact] public void EmptyMaybeObeysSecondFunctorLaw() { Func<string, int> g = s => s.Length; Func<int, bool> f = i => i % 2 == 0; var m = new Maybe<string>(); Assert.Equal(m.Select(g).Select(f), m.Select(s => f(g(s)))); }
Since m is empty, applying the translations doesn't change that fact - it only changes the type of the resulting object, which is an empty Maybe<bool>.
Haskell #
In Haskell, Maybe is built in. You can create a Maybe value containing an integer like this (the type annotations are optional):
source :: Maybe Int source = Just 42
Mapping source to a String can be done like this:
dest :: Maybe String dest = fmap show source
The function fmap corresponds to the above C# Select method.
It's also possible to use infix notation:
dest :: Maybe String dest = show <$> source
The <$> operator is an alias for fmap.
Whether you use fmap or <$>, the resulting dest value is Just "42".
If you want to create an empty Maybe value, you use the Nothing data constructor.
F# #
Maybe is also a built-in type in F#, but here it's called option instead of Maybe. You create an option containing an integer like this:
// int option let source = Some 42
While the case where a value is present was denoted with Just in Haskell, in F# it's called Some.
You can translate option values using the map function from the Option module:
// string option let dest = source |> Option.map string
Finally, if you want to create an empty option value, you can use the None case constructor.
Summary #
Together with a functor called Either, Maybe is one of the workhorses of statically typed functional programming. You aren't going to write much F# or Haskell before you run into it. In C# I've used variations of the above Maybe<T> class for years, with much success.
In this article, I only discussed Maybe in its role of being a functor, but it's so much more than that! It's also an applicative functor, a monad, and traversable (enumerable). Not all functors are that rich.
Next: An Either functor.
Comments
I think it's interesting to note that since C# 8.0 we don't require an extra generic type like Maybe<T> anymore in order to implement the maybe functor. Because C# 8.0 added nullable reference types, everything can be nullable now. By adding the right extension methods we can make T? a maybe functor and use its beautifully succinct syntax.
Due to the C#'s awkward dichotomy between value and reference types this involves some busy work, so I created a small nuget package for interested parties.
Robert, thank you for writing. That feature indeed seems like an improvement. I'm currently working in a code base with that feature enabled, and I definitely think that it's better than C# without it, but Maybe<T> it isn't. There's too many edge cases and backwards compatibility issues to make it as good.
Pragmatically, this is now what C# developers have to work with. Since it's now part of the language, it's likely that use of it will become more widespread than we could ever hope that Maybe<T> would be, so that's fine. On the other hand, Maybe<T> is now an impossible sell to C# developers.
Because of all the edge cases that the compiler could overlook, however, I don't see how this is ever going to be as good as a language without null references in the first place.
Functors
A functor is a common abstraction. While typically associated with functional programming, functors exist in C# as well.
This article series is part of a larger series of articles about functors, applicatives, and other mappable containers.
Programming is about abstraction, since you can't manipulate individual sub-atomic particles on your circuit boards. Some abstractions are well-known because they're rooted in mathematics. Particularly, category theory has proven to be fertile ground for functional programming. Some of the concepts from category theory apply to object-oriented programming as well; all you need is generics, which is a feature of both C# and Java.
In previous articles, you got an introduction to the specific Test Data Builder and Test Data Generator functors. Functors are more common than you may realise, although in programming, we usually work with a subset of functors called endofunctors. In daily speak, however, we just call them functors.
In the next series of articles, you'll see plenty of examples of functors, with code examples in both C#, F#, and Haskell. These articles are mostly aimed at object-oriented programmers curious about the concept.
- The Maybe functor
- An Either functor
- A Tree functor
- A rose tree functor
- A Visitor functor
- Reactive functor
- The Identity functor
- The Lazy functor
- Asynchronous functors
- The Const functor
- The State functor
- The Reader functor
- The IO functor
- Monomorphic functors
- Set is not a functor
IEnumerable<T>. Since the combination of IEnumerable<T> and query syntax is already well-described, I'm not going to cover it explicitly here.
If you understand how LINQ, IEnumerable<T>, and C# query syntax works, however, all other functors should feel intuitive. That's the power of abstractions.
Overview #
The purpose of this article isn't to give you a comprehensive introduction to the category theory of functors. Rather, the purpose is to give you an opportunity to learn how it translates to object-oriented code like C#. For a great introduction to functors, see Bartosz Milewski's explanation with illustrations.
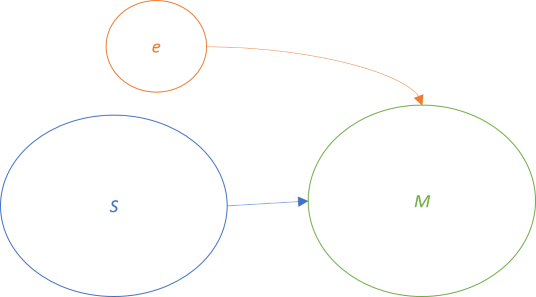
In short, a functor is a mapping between two categories. A functor maps not only objects, but also functions (called morphisms) between objects. For instance, a functor F may be a mapping between the categories C and D:
Not only does F map a from C to F a in D (and likewise for b), it also maps the function f to F f. Functors preserve the structure between objects. You'll often hear the phrase that a functor is a structure-preserving map. One example of this regards lists. You can translate a List<int> to a List<string>, but the translation preserves the structure. This means that the resulting object is also a list, and the order of values within the lists doesn't change.
In category theory, categories are often named C, D, and so on, but an example of a category could be IEnumerable<T>. If you have a function that translates integers to strings, the source object (that's what it's called, but it's not the same as an OOP object) could be IEnumerable<int>, and the destination object could be IEnumerable<string>. A functor, then, represents the ability to go from IEnumerable<int> to IEnumerable<string>, and since the Select method gives you that ability, IEnumerable<T>.Select is a functor. In this case, you sort of 'stay within' the category of IEnumerable<T>, only you change the generic type argument, so this functor is really an endofunctor (the endo prefix is from Greek, meaning within).
As a rule of thumb, if you have a type with a generic type argument, it's a candidate to be a functor. Such a type is not always a functor, because it also depends on where the generic type argument appears, and some other rules.
Fundamentally, you must be able to implement a method for your generic type that looks like this:
public Functor<TResult> Select<TResult>(Func<T, TResult> selector)
Here, I've defined the Select method as an instance method on a class called Functor<T>, but often, as is the case with IEnumerable<T>, the method is instead implemented as an extension method. You don't have to name it Select, but doing so enables query syntax in C#:
var dest = from x in source select x.ToString();
Here, source is a Functor<int> object.
If you don't name the method Select, it could still be a functor, but then query syntax wouldn't work. Instead, normal method-call syntax would be your only option. This is, however, a specific C# language feature. F#, for example, has no particular built-in awareness of functors, although most libraries name the central function map. In Haskell, Functor is a typeclass that defines a function called fmap.
The common trait is that there's an input value (Functor<T> in the above C# code snippet), which, when combined with a mapping function (Func<T, TResult>), returns an output value of the same generic type, but with a different generic type argument (Functor<TResult>).
Laws #
Defining a Select method isn't enough. The method must also obey the so-called functor laws. These are quite intuitive laws that govern that a functor behaves correctly.
The first law is that mapping the identity function returns the functor unchanged. The identity function is a function that returns all input unchanged. (It's called the identity function because it's the identity for the endomorphism monoid.) In F# and Haskell, this is simply a built-in function called id.
In C#, you can write a demonstration of the law as a unit test:
[Theory] [InlineData(-101)] [InlineData(-1)] [InlineData(0)] [InlineData(1)] [InlineData(42)] [InlineData(1337)] public void FunctorObeysFirstFunctorLaw(int value) { Func<int, int> id = x => x; var sut = new Functor<int>(value); Assert.Equal(sut, sut.Select(id)); }
While this doesn't prove that the first law holds for all values and all generic type arguments, it illustrates what's going on.
Since C# doesn't have a built-in identity function, the test creates a specialised identity function for integers, and calls it id. It simply returns all input values unchanged. Since id doesn't change the value, then Select(id) shouldn't change the functor, either. There's nothing more to the first law than this.
The second law states that if you have two functions, f and g, then mapping over one after the other should be the same as mapping over the composition of f and g. In C#, you can illustrate it like this:
[Theory] [InlineData(-101)] [InlineData(-1)] [InlineData(0)] [InlineData(1)] [InlineData(42)] [InlineData(1337)] public void FunctorObeysSecondFunctorLaw(int value) { Func<int, string> g = i => i.ToString(); Func<string, string> f = s => new string(s.Reverse().ToArray()); var sut = new Functor<int>(value); Assert.Equal(sut.Select(g).Select(f), sut.Select(i => f(g(i)))); }
Here, g is a function that translates an int to a string, and f reverses a string. Since g returns string, you can compose it with f, which takes string as input.
As the assertion points out, it shouldn't matter if you call Select piecemeal, first with g and then with f, or if you call Select with the composed function f(g(i)).
Summary #
This is not a monad tutorial; it's a functor tutorial. Functors are commonplace, so it's worth keeping an eye out for them. If you already understand how LINQ (or similar concepts in Java) work, then functors should be intuitive, because they are all based on the same underlying maths.
While this article is an overview article, it's also a part of a larger series of articles that explore what object-oriented programmers can learn from category theory.
Next: The Maybe functor.
Comments
As a rule of thumb, if you have a type with a generic type argument, it's a candidate to be a functor.
My guess is that you were thinking of Haskell's Functor typeclass when you wrote that. As Haskell documentation for Functor says,
An abstract datatypef a, which has the ability for its value(s) to be mapped over, can become an instance of theFunctortypeclass.
To explain the Haskell syntax for anyone unfamiliar, f is a generic type with type parameter a. So indeed, it is necessary to be a Haskell type to be generic to be an instance of the Functor typeclass. However, the concept of a functor in programming is not limited to Haskell's Functor typeclass.
In category theory, categories are often named C, D, and so on, but an example of a category could beIEnumerable<T>. If you have a function that translates integers to strings, the source object (that's what it's called, but it's not the same as an OOP object) could beIEnumerable<int>, and the destination object could beIEnumerable<string>. A functor, then, represents the ability to go fromIEnumerable<int>toIEnumerable<string>, and since the Select method gives you that ability,IEnumerable<T>.Selectis a functor. In this case, you sort of 'stay within' the category ofIEnumerable<T>, only you change the generic type argument, so this functor is really an endofunctor (the endo prefix is from Greek, meaning within).
For any type T including non-generic types, the category containing only a single object representing T can have (nontrivial) endofunctors. For example, consider a record of type R in F# with a field of both name and type F. Then let mapF f r = { r with F = f r.F } is the map function the satisfies the functor laws for the field F for record R. This holds even when F is not a type parameter of R. I would say that R is a functor in F.
I have realized within just the past three weeks how valuable it is to have a map function for every field of every record that I define. For example, I was able to greatly simplify the SubModelSeq sample in Elmish.WPF in part because of such map functions. I am especially pleased with the main update function, which heavily uses these map functions. It went from this to this.
In particular, I was able to eta-reduce the Model argument. To be clear, the goal is not point-free style for its own sake. Instead, it is one of perspective. In the previous implementation, the body explicitly depended on both the Msg and Model arguments and explicitly returned a Model instance. In the new implementation, the body only explicitly depends on the Msg argument and explicitly returns a function with type Model -> Model. By only having to pattern match on the Msg argument (and not having to worry about how to exactly map from one Model instance to the next), the implementation is much simpler. Such is the expressive power of high-order functions.
All this (and much more in my application at work) from realizing that a functor doesn't have to be generic.
I am looking into the possibility of generating these map functions using Myrid.
Tyson, thank you for writing. I think that you're right.
To be honest, I still find the category theory underpinnings of functional programming concepts to be a little hazy. For instance, in category theory, a functor is a mapping between categories. When category theory is translated into Haskell, people usually discuss Haskell as constituting a single large category called Hask. In that light, everything that goes on in Haskell just maps from objects in Hask to objects in Hask. In that light, I still find it difficult to distinguish between morphisms and functors.
I'm going to need to think about this some more, but my intuition is that one can also find 'smaller' categories embedded in Hask, e.g. the category of Boolean values, or the category of strings, and so on.
What I'm trying to get across is that I haven't thought enough about the boundaries of a concept such as functor. It's clear that some containers with generic types form functors, but are generics required? You argue that they aren't required, and I think that you are right.
Generics are, however, required at the language level, as you've also pointed out. I think that this is also the case for F# and C#, but I admit that since the thought hadn't crossed my mind until now, I actually don't know. If you define a Select method that takes a Func<T, T> instead of a Func<T, TResult>, does query syntax still work?
For what it's worth, there's a Haskell library that defines some type classes for monomorphic containers, including MonoFunctor. As it claims:
This strongly suggests that"All of the laws for the polymorphic typeclasses apply to their monomorphic cousins."
MonoFunctor instances are functors, too.
I agree that despite the brevity of copy-and-update expressions, the particular use case that you describe can still seem verbose to sensitive souls. It doesn't look too bad with the example you give (r.F), but usually, value and field names are longer, and then reading the field, applying a function, and setting the field again starts to feel inconvenient. I've been there.
Once you start down the path of wanting to make it easier to 'reach into' a record structure to update parts of it, you quickly encounter lenses. As far as I can tell, your map function looks equivalent to a function that the lens library calls over.
I agree that lenses can solve some real problems, and it seems that your use case was one of them.
FWIW, I recently answered a Stack Overflow question about the presence of general functors in programming. Perhaps you'll find it useful.
Also, I've now added an article about monomorphic functors.
Functors, applicatives, and friends
Functors and related data structures are containers of values. It's a family of abstractions. An overview for object-oriented programmers.
This article series is part of an even larger series of articles about the relationship between design patterns and category theory.
If you've worked with C# or Java recently, you've most likely encountered types such as Foo<T> or Bar<T> (specifically, on .NET, e.g. List<T>). Perhaps you've also noticed that often, you can translate the type inside of the container. For example, if you have a Foo<string>, perhaps you can call some method on it that returns a Foo<int>. If so, it may be a functor.
Not all generic types are functors. In order to be a functor, a generic type must obey a couple of intuitive laws. You'll learn about those in future articles.
Some functors have extra capabilities, and you'll learn about some of those as well. Some are called applicative functors, and some are called bifunctors. There are others, as well.
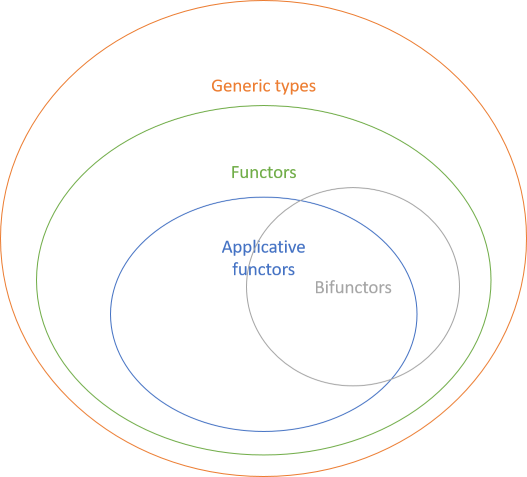
All applicative functors are functors, and this is true for bifunctors as well.
In this article series, you'll learn about the following categories:
- Functors
- Applicative functors
- Bifunctors
- Contravariant functors
- Profunctors
- Invariant functors
- Monads
- Functor relationships
Next: Functors.
Composite as a monoid
When can you use the Composite design pattern? When the return types of your methods form monoids.
This article is part of a series of articles about design patterns and their universal abstraction counterparts.
The Composite design pattern is a powerful way to structure code, but not all objects are composable. When is an object composable? This article explores that question.
In short, Composites are monoids.
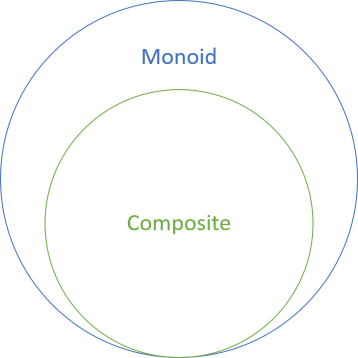
Not all monoids are Composites, but as far as I can tell, all Composites are monoids.
Composite #
First, I'll use various software design isomorphisms to put Composite in a canonical form. From unit isomorphisms, function isomorphisms, and argument list isomorphisms, we know that we can represent any method as a method or function that takes a single argument, and returns a single output value. From abstract class isomorphism we know that we can represent an abstract class with interfaces. Thus, you can represent the interface for a Composite like this:
public interface IInterface1 { Out1 Op1(In1 arg); Out2 Op2(In2 arg); Out3 Op3(In3 arg); // More operations... }
In order to create a Composite, we must be able to take an arbitrary number of implementations and make them look like a single object.
Composite as monoid #
You have a set of implementations of IInterface1. In order to create a Composite, you loop over all of those implementations in order to produce an aggregated result. Imagine that you have to implement a CompositeInterface1 class that composes imps, an IReadOnlyCollection<IInterface1>. In order to implement Op1, you'd have to write code like this:
public Out1 Op1(In1 arg) { foreach (var imp in this.imps) { var out1 = imp.Op1(arg); // Somehow combine this out1 value with previous values } // Return combined Out1 value }
This implies that we have an ordered, finite sequence of implementations: imp1, imp2, imp3, .... In C#, we could represent such a sequence with the type IReadOnlyCollection<IInterface1>. Somehow, we need to turn that collection into a single IInterface1 value. In other words, we need a translation of the type IReadOnlyCollection<IInterface1> -> IInterface1.
If we look to Haskell for inspiration for a moment, let's replace IReadOnlyCollection<T> with Haskell's built-in linked list. This means that we need a function of the type [IInterface1] -> IInterface1, or, more generally, [a] -> a. This function exists for all a as long as a forms a monoid; it's called mconcat:
mconcat :: Monoid a => [a] -> a
We also know from a previous article that a collection of monoids can be reduced to a single monoid. Notice how the above outline of a composite implementation of Op1 looks similar to the Accumulate method shown in the linked article. If IInterface1 can form a monoid, then you can make a Composite.
Objects as monoids #
When can an object (like IInterface1) form a monoid?
From object isomorphisms we know that we can decompose an object with n members to n static methods. This means that instead of analysing all of IInterface1, we can consider the properties of each method in isolation. The properties of an object is the consolidation of the properties of all the methods.
Recall, still from object isomorphisms, that we can represent an object as a tuple of functions. Moreover, if you have a tuple of monoids, then the tuple also forms monoid!
In order to make an object a monoid, then, you have to make each method a monoid. When is a method a monoid? A method is a monoid when its return type forms a monoid.
That's it. An interface like IInterface1 is a monoid when Out1, Out2, Out3, and so on, form monoids. If that's the case, you can make a Composite.
Examples #
From unit isomorphism, we know that we can represent C#'s and Java's void keywords with methods returning unit, and unit is a monoid. All methods that return void can be part of a Composite, but we already knew that Commands are composable. If you search for examples of the Composite design pattern, you'll find more than one variation involving drawing shapes on a digital canvas, with the central operation being a Draw method with a void return type.
Another example could be calculation of the price of a shopping basket. If you have an interface method of the type decimal Calculate(Basket basket), you could have several implementations:
- Add all the item prices together
- Apply a discount (a negative number)
- Calculate sales tax
Boolean values also form at least two monoids (any and all), so any method you have that returns a Boolean value can be used in a Composite. You could, for example, have a list of criteria for granting a loan. Each such business rule returns true if it evaluates that the loan should be granted, and false otherwise. If you have more than one business rule, you can create a Composite that returns true only if all the individual rules return true.
If you have a method that returns a string, then that is also a candidate for inclusion in a Composite, if string concatenation makes sense in the domain in question.
You probably find it fairly mundane that you can create a Composite if all the methods involved return numbers, strings, Booleans, or nothing. The result generalises, however, to all monoids, including more complex types, including methods that return other interfaces that themselves form monoids, and so on recursively.
Granularity #
The result, then, is that you can make a Composite when all methods in your interface have monoidal return types. If only a single method has a return type that isn't a monoid, you can't aggregate that value, and you can't make a Composite.
Your interface can have as many methods you like, but they must all be monoids. Even one rogue method will prevent you from being able to create a Composite. This is another argument for Role Interfaces. The smaller an interface is, the more likely it is that you can make a Composite out of it. If you follow that line of reasoning to its ultimate conclusion, you'll design your interfaces with a single member each.
Relaxation #
There can be some exceptions to the rule that all return values must be monoids. If you have at least one implementation of your interface, then a semigroup may be enough. Recall that monoids accumulate like this:
public static Foo Accumulate(IReadOnlyCollection<Foo> foos) { var acc = Identity; foreach (var f in foos) acc = acc.Op(f); return acc; }
You only need Identity in order to start the accumulation, and to have something to return in case you have no implementations. If you have at least one implementation, you don't need the identity, and then a semigroup is enough to accumulate. Consider the bounding box example. If you have a method that returns BoundingBox values, you can still make a Composite out of such an interface, as long as you have at least one implementation. There's no 'identity' bounding box, but it makes intuitive sense that you can still compose bounding boxes into bigger bounding boxes.
Haskell formalises the rule for semigroups:
sconcat :: Semigroup a => Data.List.NonEmpty.NonEmpty a -> a
The sconcat function reduces any non-empty list of any semigroup a to a single a value.
If you have a non-empty list of implementations, then perhaps you don't even need a semigroup. Perhaps any magma will work. Be aware, however, that the lack of associativity will cause the order of implementations to matter.
Technically, you may be able to program a Composite from a magma, but I'd suggest caution. The monoid and semigroup laws are intuitive. A magma without those properties may not form an intuitive Composite. While it may compile, it may have surprising, or counter-intuitive, behaviour. I'd favour sticking to monoids or semigroups.
Summary #
When is an object-oriented design composable? Composition could mean more than one thing, but this article has focused exclusively on the Composite design pattern. When can you use the Composite pattern? When all method return types are monoids.
Some design patterns as universal abstractions
Some design patterns can be formalised by fundamental abstractions.
This article series submits results based on the work presented in an even larger series of articles about the relationship between design patterns and category theory.
Wouldn't it be wonderful if you could assemble software from predefined building blocks? This idea is old, and has been the driving force behind object-oriented programming (OOP). In Douglas Coupland's 1995 novel Microserfs, the characters attempt to reach that goal through a project called Oop!. Lego bricks play a role as a metaphor as well.

Decades later, it doesn't look like we're much nearer that goal than before, but I believe that we'd made at least two (rectifiable) mistakes along the way:
- Granularity
- Object-orientation
Granularity #
Over the years, I've seen several attempts at reducing software development to a matter of putting things together. These attempts have invariably failed.
I believe that one of the reasons for failure is that such projects tend to aim at coarse-grained building blocks. As I explain in the Interface Segregation Principle module of my Encapsulation and SOLID Pluralsight course, granularity is a crucial determinant for your ability to create. The coarser-grained the building blocks, the harder it is to create something useful.
Most attempts at software-as-building-blocks have used big, specialised building blocks aimed at non-technical users ("Look! Create an entire web site without writing a single line of code!"). That's just like Duplo. You can create exactly what the blocks were designed for, but as soon as you try to create something new and original, you can't.
Object-orientation #
OOP is another attempt at software-as-building-blocks. In .NET (the OOP framework with which I'm most familiar) the Base Class Library (BCL) is enormous. Many of the reusable objects in the BCL are fine-grained, so at least it's often possible to put them together to create something useful. The problem with an object-oriented library like the .NET BCL, however, is that all the objects are special.
The vision was always that software 'components' would be able to 'click' together, just like Lego bricks. The BCL isn't like that. Typically, objects have nothing in common apart from the useless System.Object base class. There's no system. In order to learn how the BCL works, you have to learn the ins and outs of every single class.
Better know a framework.
It doesn't help that OOP was never formally defined. Every time you see or hear a discussion about what 'real' object-orientation is, you can be sure that sooner or later, someone will say: "...but that's not what Alan Kay had in mind."
What Alan Kay had in mind is still unclear to me, but it seems safe to say that it wasn't what we have now (C++, Java, C#).
Building blocks from category theory #
While we (me included) have been on an a thirty-odd year long detour around object-orientation, I don't think all is lost. I still believe that a Lego-brick-like system exists for software development, but I think that it's a system that we have to discover instead of invent.
As I already covered in the introductory article, category theory does, in fact, discuss 'objects'. It's not the same type of object that you know from C# or Java, but some of them do consist of data and behaviour - monoids, for example, or functors. Such object are more like types than objects in the OOP sense.
Another, more crucial, difference to object-oriented programming is that these objects are lawful. An object is only a monoid if it obeys the monoid laws. An object is only a functor if it obeys the functor laws.
Such objects are still fine-grained building blocks, but they fit into a system. You don't have to learn tens of thousands of specific objects in order to get to know a framework. You need to understand the system. You need to understand monoids, functors, applicatives, and a few other universal abstractions (yes: monads too).
Many of these universal abstractions were almost discovered by the Gang of Four twenty years ago, but they weren't quite in place then. Much of that has to do with the fact that functional programming didn't seem like a realistic alternative back then, because of hardware limitations. This has all changed to the better.
Specific patterns #
In the introductory article about the relationship between design patterns and category theory, you learned that some design patterns significantly overlap concepts from category theory. In this article series, we'll explore the relationships between some of the classic patterns and category theory. I'm not sure that all the patterns from Design Patterns can be reinterpreted as universal abstractions, but the following subset seems promising:
- Composite as a monoid
- Null Object as identity
- Builder as a monoid
- Visitor as a sum type
- Chain of Responsibility as catamorphisms
- The State pattern and the State monad
- Postel's law as a profunctor
- The Liskov Substitution Principle as a profunctor
- Backwards compatibility as a profunctor
Summary #
Some design patterns closely resemble categorical objects. This article provides an overview, whereas the next articles in the series will dive into specifics.
Next: Composite as a monoid.
Inheritance-composition isomorphism
Reuse via inheritance is isomorphic to composition.
This article is part of a series of articles about software design isomorphisms.
Chapter 1 of Design Patterns admonishes:
Favor object composition over class inheritancePeople sometimes struggle with this, because they use inheritance as a means to achieve reuse. That's not necessary, because you can use object composition instead.
In the previous article, you learned that an abstract class can be refactored to a concrete class with injected dependencies.
Did you notice that there was an edge case that I didn't cover?
I didn't cover it because I think it deserves its own article. The case is when you want to reuse a base class' functionality in a derived class. How do you do that with Dependency Injection?
Calling base #
Imagine a virtual method:
public virtual OutVirt1 Virt1(InVirt1 arg)
In C#, a method is virtual when explicitly marked with the virtual keyword, whereas this is the default in Java. When you override a virtual method in a derived class, you can still invoke the parent class' implementation:
public override OutVirt1 Virt1(InVirt1 arg) { // Do stuff with this and arg var baseResult = base.Virt1(arg); // return an OutVirt1 value }
When you override a virtual method, you can use the base keyword to invoke the parent implementation of the method that you're overriding. The enables you to reuse the base implementation, while at the same time adding new functionality.
Virtual method as interface #
If you perform the refactoring to Dependency Injection shown in the previous article, you now have an interface:
public interface IVirt1 { OutVirt1 Virt1(InVirt1 arg); }
as well as a default implementation. In the previous article, I showed an example where a single class implements several 'virtual member interfaces'. In order to make this particular example clearer, however, here you instead see a variation where the default implementation of IVirt1 is in a class that only implements that interface:
public class DefaultVirt1 : IVirt1 { public OutVirt1 Virt1(InVirt1 arg) { // Do stuff with this and arg; return an OutVirt1 value. } }
DefaultVirt1.Virt1 corresponds to the original virtual method on the abstract class. How can you 'override' this default implementation, while still make use of it?
From base to composition #
You have a default implementation, and instead of replacing all of it, you want to somehow enhance it, but still use the 'base' implementation. Instead of inheritance, you can use composition:
public class OverridingVirt1 : IVirt1 { private readonly IVirt1 @base = new DefaultVirt1(); public OutVirt1 Virt1(InVirt1 arg) { // Do stuff with this and arg var baseResult = @base.Virt1(arg); // return an OutVirt1 value } }
In order to drive home the similarity, I named the class field @base. I couldn't use base as a name, because that's a keyword in C#, but you can use the prefix @ in order to use a keyword as a legal C# name. Notice that the body of OverridingVirt1.Virt1 is almost identical to the above, inheritance-based overriding method.
As a variation, you can inject @base via the constructor of OverridingVirt1, in which case you have a Decorator.
Isomorphism #
If you already have an interface with a 'default implementation', and you want to reuse the default implementation, then you can use object composition as shown above. At its core, it's reminiscent of the Decorator design pattern, but instead of receiving the inner object via its constructor, it creates the object itself. You can, however, also use a Decorator in order to achieve the same effect. This will make your code more flexible, but possibly also more error-prone, because you no longer have any guarantee what the 'base' is. This is where the Liskov Substitution Principle becomes important, but that's a digression.
If you're using the previous abstract class isomorphism to refactor to Dependency Injection, you can refactor any use of base to object composition as shown here.
This is a special case of Replace Inheritance with Delegation from Refactoring, which also describes the inverse refactoring Replace Delegation with Inheritance, thereby making these two refactorings an isomorphism.
Summary #
This article focuses on a particular issue that you may run into if you try to avoid the use of abstract classes. Many programmers use inheritance in order to achieve reuse, but this is in no way necessary. Favour composition over inheritance.
Next: Tester-Doer isomorphisms.
Abstract class isomorphism
Abstract classes are isomorphic to Dependency Injection.
This article is part of a series of articles about software design isomorphisms.
The introduction to Design Patterns states:
Program to an interface, not an implementation.When I originally read that, I took it quite literally, so I wrote all my C# code using interfaces instead of abstract classes. There are several reasons why, in general, that turns out to be a good idea, but that's not the point of this article. It turns out that it doesn't really matter.
If you have an abstract class, you can refactor to an object model composed from interfaces without loss of information. You can also refactor back to an abstract class. These two refactorings are each others' inverses, so together, they form an isomorphism.
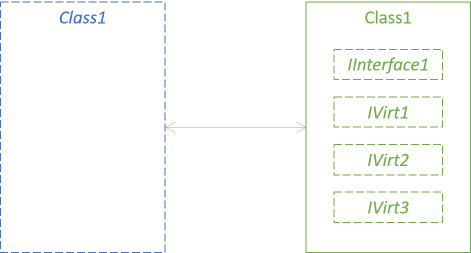
When refactoring an abstract class, you extract all its pure virtual members to an interface, each of its virtual members to other interfaces, and inject them into a concrete class. The inverse refactoring involves going back to an abstract class.
This is an important result, because upon closer inspection, the Gang of Four didn't have C# or Java interfaces in mind. The book pre-dates both Java and C#, and its examples are mostly in C++. Many of the examples involve abstract classes, but more than ten years of experience has taught me that I can always write a variant that uses C# interfaces. That is, I believe, not a coincidence.
Abstract class #
An abstract class in C# has this general shape:
public abstract class Class1 { public Data1 Data { get; set; } public abstract OutPureVirt1 PureVirt1(InPureVirt1 arg); public abstract OutPureVirt2 PureVirt2(InPureVirt2 arg); public abstract OutPureVirt3 PureVirt3(InPureVirt3 arg); // More pure virtual members... public virtual OutVirt1 Virt1(InVirt1 arg) { // Do stuff with this, Data, and arg; return an OutVirt1 value. } public virtual OutVirt2 Virt2(InVirt2 arg) { // Do stuff with this, Data, and arg; return an OutVirt2 value. } public virtual OutVirt3 Virt3(InVirt3 arg) { // Do stuff with this, Data, and arg; return an OutVirt3 value. } // More virtual members... public OutConc1 Op1(InConc1 arg) { // Do stuff with this, Data, and arg; return an OutConc1 value. } public OutConc2 Op2(InConc2 arg) { // Do stuff with this, Data, and arg; return an OutConc2 value. } public OutConc3 Op3(InConc3 arg) { // Do stuff with this, Data, and arg; return an OutConc3 value. } // More concrete members... }
Like in the previous article, I've deliberately kept the naming abstract (but added a more concrete example towards the end). The purpose of this article series is to look at the shape of code, instead of what it does, or why. From argument list isomorphisms we know that we can represent any method as taking a single input value, and returning a single output value.
An abstract class can have non-virtual members. In C#, this is the default, whereas in Java, you'd explicitly have to use the final keyword. In the above generalised representation, I've named these non-virtual members Op1, Op2, and so on.
An abstract class can also have virtual members. In C#, you must explicitly use the virtual keyword in order to mark a method as overridable, whereas this is the default for Java. In the above representation, I've called these methods Virt1, Virt2, etcetera.
Some virtual members are pure virtual members. These are members without an implementation. Any concrete (that is: non-abstract) class inheriting from an abstract class must provide an implementation for such members. In both C# and Java, you must declare such members using the abstract keyword. In the above representation, I've called these methods PureVirt1, PureVirt2, and so on.
Finally, an abstract class can contain data, which you can represent as a single data object, here of the type Data1.
The concrete and virtual members could, conceivably, call other members in the class - both concrete, virtual, and pure virtual. In fact, this is how many of the design patterns in the book work, for example Strategy, Template Method, and Builder.
From abstract class to Dependency Injection #
Apart from its Data, an abstract class contains three types of members:
- Those that must be implemented by derived classes: pure virtual members
- Those that optionally can be overriden by derived classes: virtual members
- Those that cannot be overridden by derived classes: concrete, sealed, or final, members
- Extract an interface from the pure virtual members.
- Extract an interface from each of the virtual members.
- Implement each of the 'virtual member interfaces' with the implementation from the virtual member.
- Add a constructor to the abstract class that takes all these new interfaces as arguments. Save the arguments as class fields.
- Change all code in the abstract class to talk to the injected interfaces instead of direct class members.
- Remove the virtual and pure virtual members from the class, or make them non-virtual. If you keep them around, their implementation should be one line of code, delegating to the corresponding interface.
- Change the class to a concrete (non-abstract) class.
public sealed class Class1 { private readonly IInterface1 pureVirts; private readonly IVirt1 virt1; private readonly IVirt2 virt2; private readonly IVirt3 virt3; // More virt fields... public Data1 Data { get; set; } public Class1( IInterface1 pureVirts, IVirt1 virt1, IVirt2 virt2, IVirt3 virt3 /* More virt arguments... */) { this.pureVirts = pureVirts; this.virt1 = virt1; this.virt2 = virt2; this.virt3 = virt3; // More field assignments } public OutConc1 Op1(InConc1 arg) { // Do stuff with this, Data, and arg; return an OutConc1 value. } public OutConc2 Op2(InConc2 arg) { // Do stuff with this, Data, and arg; return an OutConc2 value. } public OutConc3 Op3(InConc3 arg) { // Do stuff with this, Data, and arg; return an OutConc3 value. } // More concrete members... }
While not strictly necessary, I've marked the class sealed (final in Java) in order to drive home the point that this is no longer an abstract class.
This is an example of the Constructor Injection design pattern. (This is not a Gang of Four pattern; you can find a description in my book about Dependency Injection.)
Since it's optional to override virtual members, any class originally inheriting from an abstract class can choose to override only one, or two, of the virtual members, while leaving other virtual members with their default implementations. In order to support such piecemeal redefinition, you can extract each virtual member to a separate interface, like this:
public interface IVirt1 { OutVirt1 Virt1(InVirt1 arg); }
Notice that each of these 'virtual interfaces' are injected into Class1 as a separate argument. This enables you to pass your own implementation of exactly those you wish to change, while you can pass in the default implementation for the rest. The default implementations are the original code from the virtual members, but moved to a class that implements the interfaces:
public class DefaultVirt : IVirt1, IVirt2, IVirt3
When inheriting from the original abstract class, however, you must implement all the pure virtual members, so you can extract a single interface from all the pure virtual members:
public interface IInterface1 { OutPureVirt1 PureVirt1(InPureVirt1 arg); OutPureVirt2 PureVirt2(InPureVirt2 arg); OutPureVirt3 PureVirt3(InPureVirt3 arg); // More pure virtual members... }
This forces anyone who wants to use the refactored (sealed) Class1 to provide an implementation of all of those members. There's an edge case where you inherit from the original Class1 in order to create a new abstract class, and implement only one or two of the pure virtual members. If you want to support that edge case, you can define an interface for each pure virtual member, instead of one big interface, similar to IVirt1, IVirt2, and so on.
From Dependency Injection to abstract class #
I hope it's clear how to perform the inverse refactoring. Assume that the above sealed Class1 is the starting point:
- Mark
Class1asabstract. - For each of the members of
IInterface1, add a pure virtual member. - For each of the members of
IVirt1,IVirt2, and so on, add a virtual member. - Move the code from the default implementation of the 'virtual interfaces' to the new virtual members.
- Delete the dependency fields and remove the corresponding arguments from the constructor.
- Clean up orphaned interfaces and implementations.
Example: Gang of Four maze Builder as an abstract class #
As an example, consider the original Gang of Four example of the Builder pattern. The example in the book is based on an abstract class called MazeBuilder. Translated to C#, it looks like this:
public abstract class MazeBuilder { public virtual void BuildMaze() { } public virtual void BuildRoom(int room) { } public virtual void BuildDoor(int roomFrom, int roomTo) { } public abstract Maze GetMaze(); }
In the book, all four methods are virtual, because:
"They're not declared pure virtual to let derived classes override only those methods in which they're interested."When it comes to the
GetMaze method, this means that the method in the book returns a null reference by default. Since this seems like poor API design, and also because the example becomes more illustrative if the class has both abstract and virtual members, I changed it to be abstract (i.e. pure virtual).
In general, there are various other issues with this design, the most glaring of which is the implied sequence coupling between members: you're expected to call BuildMaze before any of the other methods. A better design would be to remove that explicit step entirely, or else turn it into a factory that you have to call in order to be able to call the other methods. That's not the topic of the present article, so I'll leave the API like this.
The book also shows a simple usage example of the abstract MazeBuilder class:
public class MazeGame { public Maze CreateMaze(MazeBuilder builder) { builder.BuildMaze(); builder.BuildRoom(1); builder.BuildRoom(2); builder.BuildDoor(1, 2); return builder.GetMaze(); } }
You use it with e.g. a StandardMazeBuilder like this:
var game = new MazeGame(); var builder = new StandardMazeBuilder(); var maze = game.CreateMaze(builder);
You could also, again following the book's example as closely as possible, use it with a CountingMazeBuilder, like this:
var game = new MazeGame(); var builder = new CountingMazeBuilder(); game.CreateMaze(builder); var msg = $"The maze has {builder.RoomCount} rooms and {builder.DoorCount} doors.";
This would produce "The maze has 2 rooms and 1 doors.".
Both StandardMazeBuilder and CountingMazeBuilder are concrete classes that derive from the abstract MazeBuilder class.
Maze Builder refactored to interfaces #
If you follow the refactoring outline in this article, you can refactor the above MazeBuilder class to a set of interfaces. The first should be an interface extracted from all the pure virtual members of the class. In this example, there's only one such member, so the interface becomes this:
public interface IMazeBuilder { Maze GetMaze(); }
The three virtual members each get their own interface, so that you can pick and choose which of them you want to override, and which of them you prefer to keep with their default implementation (which, in this particular case, is to do nothing).
The first one was difficult to name:
public interface IMazeInitializer { void BuildMaze(); }
An interface with a single method called BuildMaze would naturally have a name like IMazeBuilder, but unfortunately, I just used that name for the previous interface. The reason I named the above interface IMazeBuilder is because this is an interface extracted from the MazeBuilder abstract class, and I consider the pure virtual API to be the core API of the abstraction, so I think it makes most sense to keep the name for that interface. Thus, I had to come up with a smelly name like IMazeInitializer.
Fortunately, the two remaining interfaces are a little better:
public interface IRoomBuilder { void BuildRoom(int room); } public interface IDoorBuilder { void BuildDoor(int roomFrom, int roomTo); }
The three virtual members all had default implementations, so you need to keep those around. You can do that by moving the methods' code to a new class that implements the new interfaces:
public class DefaultMazeBuilder : IMazeInitializer, IRoomBuilder, IDoorBuilder
In this example, there's no reason to show the implementation of the class, because, as you may recall, all three methods are no-ops.
Instead of inheriting from MazeBuilder, implementers now implement the appropriate interfaces:
public class StandardMazeBuilder : IMazeBuilder, IMazeInitializer, IRoomBuilder, IDoorBuilder
This version of StandardMazeBuilder implements all four interfaces, since, before, it overrode all four methods. CountingMazeBuilder, on the other hand, never overrode BuildMaze, so it doesn't have to implement IMazeInitializer:
public class CountingMazeBuilder : IRoomBuilder, IDoorBuilder, IMazeBuilder
All of these changes leaves the original MazeBuilder class defined like this:
public class MazeBuilder : IMazeBuilder, IMazeInitializer, IRoomBuilder, IDoorBuilder { private readonly IMazeBuilder mazeBuilder; private readonly IMazeInitializer mazeInitializer; private readonly IRoomBuilder roomBuilder; private readonly IDoorBuilder doorBuilder; public MazeBuilder( IMazeBuilder mazeBuilder, IMazeInitializer mazeInitializer, IRoomBuilder roomBuilder, IDoorBuilder doorBuilder) { this.mazeBuilder = mazeBuilder; this.mazeInitializer = mazeInitializer; this.roomBuilder = roomBuilder; this.doorBuilder = doorBuilder; } public void BuildMaze() { this.mazeInitializer.BuildMaze(); } public void BuildRoom(int room) { this.roomBuilder.BuildRoom(room); } public void BuildDoor(int roomFrom, int roomTo) { this.doorBuilder.BuildDoor(roomFrom, roomTo); } public Maze GetMaze() { return this.mazeBuilder.GetMaze(); } }
At this point, you may decide to keep the old MazeBuilder class around, because you may have other code that relies on it. Notice, however, that it's now a concrete class that has dependencies injected into it via its constructor. All four members only delegate to the relevant dependencies in order to do actual work.
MazeGame looks like before, but calling CreateMaze looks more complicated:
var game = new MazeGame(); var builder = new StandardMazeBuilder(); var maze = game.CreateMaze(new MazeBuilder(builder, builder, builder, builder));
Notice that while you're passing four dependencies to the MazeBuilder constructor, you can reuse the same StandardMazeBuilder object for all four roles.
If you want to count the rooms and doors, however, CountingMazeBuilder doesn't implement IMazeInitializer, so for that role, you'll need to use the default implementation:
var game = new MazeGame(); var builder = new CountingMazeBuilder(); game.CreateMaze(new MazeBuilder(builder, new DefaultMazeBuilder(), builder, builder)); var msg = $"The maze has {builder.RoomCount} rooms and {builder.DoorCount} doors.";
If, at this point, you're beginning to wonder what value MazeBuilder adds, then I think that's a legitimate concern. What often happens, then, is that you simply remove that extra layer.
Mazes without MazeBuilder #
When you delete the MazeBuilder class, you'll have to adjust MazeGame accordingly:
public class MazeGame { public Maze CreateMaze( IMazeInitializer initializer, IRoomBuilder roomBuilder, IDoorBuilder doorBuilder, IMazeBuilder mazeBuilder) { initializer.BuildMaze(); roomBuilder.BuildRoom(1); roomBuilder.BuildRoom(2); doorBuilder.BuildDoor(1, 2); return mazeBuilder.GetMaze(); } }
The CreateMaze method now simply takes the four interfaces on which it relies as individual arguments. This simplifies the client code as well:
var game = new MazeGame(); var builder = new StandardMazeBuilder(); var maze = game.CreateMaze(builder, builder, builder, builder);
You can still reuse a single StandardMazeBuilder in all roles, but again, if you only want to count the rooms and doors, you'll have to rely on DefaultMazeBuilder for the behaviour that CountingMazeBuilder doesn't define:
var game = new MazeGame(); var builder = new CountingMazeBuilder(); game.CreateMaze(new DefaultMazeBuilder(), builder, builder, builder); var msg = $"The maze has {builder.RoomCount} rooms and {builder.DoorCount} doors.";
The order in which dependencies are passed to CreateMaze is different than the order they were passed to the now-deleted MazeBuilder constructor, so you'll have to pass a new DefaultMazeBuilder() as the first argument in order to fill the role of IMazeInitializer. Another way to address this issue is to supply various overloads of the CreateMaze method that uses DefaultMazeBuilder for the behaviour that you don't want to override.
Summary #
Many of the original design patterns in Design Patterns are described with examples in C++, and many of these examples use abstract classes as the programming interfaces that the Gang of Four really had in mind when they wrote that we should be programming to interfaces instead of implementations.
The most important result of this article is that you can reinterpret the original design patterns with C# or Java interfaces and Dependency Injection, instead of using abstract classes. I've done this in C# for more than ten years, and in my experience, you never need abstract classes in a greenfield code base. There's always an equivalent representation that involves composition of interfaces.
Comments
While the idea is vey interesting I think it is not exactly an isomorphism.
The first reason I think it is not an isomorphism is language-specific since Java and C# allow implementing multiple interfaces but not multiple abstract classes. It can make a reverse transformation from interfaces back to an abstract class non-trivial.
The second reason is that abstract class guarantees that whatever class implements the pure virtual members and overrides virtual members share the same state between all its methods and also with the abstract base class. With the maze Builder example there must be a state shared between GetMaze, BuildMaze, BuildRoom and BuildDoor methods but the dependency injection does not seem to reflect it.
Perhaps there should be some kind of Data parameter passed to all injected interfaces.
Max, thank you for writing, and particularly for applying critique to this post. One of my main motivations for writing the entire article series is that I need to subject my thoughts to peer review. I've been thinking about these things for years, but in order to formalise them, I need to understand whether I'm completely wrong (I hope not), of, if I'm not, what are the limits of my findings.
I think you've just pointed at one such limit, and for that I'm grateful. The rest of this answer, then, is not an attempt to refute your comment, but rather an effort to identify some constraints within which what I wrote may still hold.
Your second objection doesn't worry me that much, because you also suggest a way around it. I admit that I faked the Maze Builder code somewhat, so that the state isn't explicit. I feel that fudging the code example is acceptable, as the Gang of Four code example is also clearly incomplete. In any case, you're right that an abstract class could easily contain some shared state. When refactoring to interfaces, the orchestrating class could instead pass around that state as an argument to all methods, as you suggest. Would it be reasonable to conclude that this, then, doesn't prevent the translations from being isomorphic?
There's still your first objection, which I think is significant. That's the reason I decided to cover your second objection first, because I think it'll require more work to address the first objection.
First, I think we need to delimit the problem, since your comment slightly misrepresents my article. The claim in the article is that you can refactor an abstract class to a concrete class with injected dependencies. Furthermore, the article claims that this translation is isomorphic; i.e. that you can refactor a concrete class with injected dependencies to an abstract class.
If I read your comment right, you're saying that a class can implement more than one interface, like this:
public class MyClass : IFoo, IBar
I agree that you can't use the transformations described in this article to refactor MyClass to an abstract class, because that's not the transformation that the article describes.
That doesn't change that your comment is uncomfortably close to an inconvenient limitation. You're right that there seems to be a limitation when it comes to C#'s and Java's lack of multiple inheritance. As your comment implies, if a translation is isomorphic, one has to be able to start at either end, and round-trip to the other end and back. Thus, one has to be able to start with a concrete class with injected dependencies, and refactor to an abstract class; for example:
public class MyClass { public MyClass(IFoo foo, IBar bar) { // ... } }
As far as I can tell, that's exactly the shape of the sealed version of Class1, above, so I'm not convinced that that's a problem, but something like the following does look like a problem to me:
public class MyClass { public MyClass(IFoo foo1, IFoo foo2) { // ... } }
It's not clear to me how one can refactor something like that to an abstract class, and still retain the distinction between foo1 and foo2. My claim is not that this is impossible, but only that it's not immediately clear to me how to do that. Thus, we may have to put a constraint on the original claim, and instead say something like this:
An abstract class is isomorphic to a concrete class with injected dependencies, given that all the injected dependencies are of different types.We can attempt to illustrate the claim like this:
This is still an isomorphism, I think, although I invite further criticism of that claim. Conceptual Mathematics defines an isomorphism in terms of categories A and B, and as far as I can tell, A and B can be as specific as we want them to be. Thus, we can say that A is the set of abstract classes, and B is the subset of concrete classes with injected dependencies, for which no dependency share the same type.
If we have to constrain the isomorphism in this way, though, is it still interesting? Why should we care?
To be perfectly honest, what motivated me to write this particular article is that I wanted to describe the translation from an abstract class to dependency injection. The inverse interests me less, but I thought that if the inverse translation exists, I could fit this article in with the other articles in this article series about software design isomorphisms.
The reason I care about the translation from abstract class to dependency injection is that I often see code where the programmers misuse inheritance. My experience with C# is that one can completely avoid inheritance. The way to do that is to use dependency injection instead. This article shows how to do that.
The result that one can write real, complex code bases in C# without inheritance is important to me, because one of my current goals is to teach people the advantages of functional programming, and one barrier I run into is that people who come from object-oriented programming run into problems when they no longer can use inheritance. Thus, this article shows an object-oriented alternative to inheritance, so that people can get used to the idea of designing without inheritance, even before they start looking at functional programming.
Another motivation for this article is that it's part of a much larger article series about design patterns, and how they relate to fundamental abstractions. In Design Patterns, all the (C++) patterns are described in terms of inheritance, so I wrote this article series on isomorphisms in order to be able to represent various design patterns in other forms than they appear in the book.
This idea is a very interesting and useful one, but as I found out in one of my toy projects and as Max stated above, it is unfortunately not language agnostic.
As far as C# is concerned, you can have operator overloading in an abstract class, which is a bit of logic that I see no way of extracting to an interface and thus remove the need for inheritance. Example below.
(You could define Add, Subtract, Multiply and Divide methods, but to me they seem like reinventing the square wheel. They seem much less convenient than +-*/)
I tried creating some nice Temperature value objects, similar to the money monoid you presented and I came up with 5 classes:
Temperature, Kelvin, Celsius, Fahrenheit and TemperatureExpression.
Temperature is the abstract class and its +Temperature and -Temperature operators are overloaded so that they return a TemperatureExpression, which can then be evaluated to a Maybe<TTemperature> where TTemperature : Temperature.
A TemperatureExpression is nothing more than a lazily evaluated mathematical expression (for example: 12K + 24C - 32F).
Also, it's a Maybe because 0K - 1C won't be a valid temperature, so we have to also take this case into consideration.
For further convenience, the Kelvin class has its own overloaded + operator, because no matter what you do, when adding together two Kelvin values you'll always end up with something that is greater than 0.
These being said, if you want to leverage the C# operators there are some limitations regarding this transformation that keep you from having this abstract class -> DI isomorphism.
That is, unless you're willing to add the methods I've spoken of in the first paragraph.
But, in an ideal programming language, IMHO, arithmetic and boolean operators should be part of some public interfaces like, ISubtractable, IDivideable and thus allow for a smooth transition between abstract classes and interface DI.
Ciprian, thank you for writing. I agree that this isn't language agnostic. It's possible that we need to add further constraints to the conjecture, but I still anticipate that, with appropriate constraints, it holds for statically typed 'mainstream' object-oriented languages (i.e. C# and Java). It may also hold for other languages, but it requires detailed knowledge of a language to claim that it does. For instance, it's been too long since I wrote C++ code, and I can't remember how its object-oriented language features work. Likewise, it'd be interesting to investigate if the conjecture holds when applied to JavaScript, Ruby, Python, etc., but I've been careful not to claim that, as I know too little about those languages.
Regarding your temperature example, I think that perhaps I understand what the issue is, but I'm not sure I've guessed right. In the interest of being able to have an unambiguous discussion about a code example, could you please post the pertinent code that illustrates your point?
I've added the code to github. I think it's better than copy-pasting here as you can gain some extra context.
It's a playground project where I put to practice various ideas I find on the web (so if you see something you consider should be done otherwise, I don't mind you saying it). I've added a few comments to make it a bit easier to understand and also removed anything that doesn't pertain to the issue with abstract class -> DI.
In short, the bit of logic that I can't see a way of extracting to some sort of injectable dependency are the +- operators on the Temperature class due to the fact that they are static methods, thus cannot be part of an interface (at least in C#, I don't know about programming languages).
Ciprian, thank you for elaborating. I'd forgotten about C#'s ability to overload arithmetic operators, which is, I believe, what you're referring to. To be clear, I do believe that it's a fair enough critique, so that we'll have to once again restrict this article's conjecture to something like:
There exists a subset A of all abstract classes, and a subset of all concrete classes with injected dependencies I, such that an isomorphism A <-> I exists.In diagram form, it would look like this:
By its shape, the diagram suggests that the size of abstract classes not isomorphic with Dependency Injection is substantial, but that's not really my intent; I just had to leave room for the text.
My experience suggests to me that most abstract classes can be refactored as I've described in this article, but clearly, as you've shown, there are exceptions. C#'s support for operator overloading is one such exception, but there may be others of which I'm currently ignorant.
That said, I would like to make the case that arithmetic operators aren't object-oriented in the first place. Had the language been purely object-oriented from the outset, addition would more appropriately have had a syntax like 40.Add(2). This would imply that the language would have been based on the concept of objects as data with behaviour, and the behaviour would exclusively have been defined by class members.
Even at the beginning, though, C# was a hybrid language. It had (and still has) a subset of language features focused on more low-level programming. It has value types in addition to reference types, it has arithmetic operators, it has special support for bitwise Boolean operators, and it even has pointers.
There are practical reasons that all of those features exist, but I would claim that none of those features have anything to do with object-orientation.
Specifically when it comes to arithmetic operators, the operators are all special cases baked into the language. The selection of operators is sensible, but when you get to the bottom of it, arbitrary. For instance, there's a modulo operator, but no power operator. Why?
As an aside, languages do exist where arithmetic is an abstraction instead of a language feature. The one I'm most familiar with is Haskell, where arithmetic is defined in terms of type classes. It's worth noting that the operators +, *, and - are defined in an abstraction called Num, whereas the 'fourth' arithmetic operator / is defined in a more specialised abstraction called Fractional.
Not that Haskell's model of arithmetic is perfect, but there's a rationale behind this distinction. Division is special, because it can translate two integers (e.g. 2 and 3) into a rational number (e.g. 2/3), while both addition and multiplication are monoids. This is where Haskell starts to fall apart itself, though, because subtraction can also translate two numbers out of the set in which they originally belonged. For example, given two natural numbers 2 and 3, 2 - 3 is no longer a natural number, since it's negative.
But all of that is an aside. Even in C#, one has to deal with low-level exceptional cases such as integer overflow, so even addition isn't truly monoidal, unless you use BigInteger.
Mark, thank you for the detailed response. I didn't mean to refute the usefulness of the refactoring you described. I now see how I tried to apply the refactoring of DI to abstact class where it was not claimed to be possible.
I've been thinking about the example with the injection of distinct instances of the same type. I think we can use simple wrapper types for this kind of problem:
public sealed class Foo1 : IFoo { private readonly IFoo impl_; public Foo1 (IFoo impl) { impl_ = impl; } public Out1 Op1 (In1 in1) { return impl_.Op1 (in1); } }
Foo1 implements IFoo to keep the ability to e.g. create a list of foo1 and foo2.
Given such wrappers are created for all dependencies of type IFoo, MyClass can be rewritten like this:
public class MyClass { public MyClass (Foo1 foo1, Foo2 foo2) { // ... } }
Now MyClass can be refactored into an abstract class without losing the distinction between foo1 and foo2.
I also belive that, given the wrappers are used only in the context of MyClass, the use of wrappers and diffent fields or parameters is an isomorphism. While its usefulness as a stand-alone refactoing is limited, it may come handy for reasoning similar to the one you did in Composite as a monoid.
Thin wrappers can be used to create an almost convenient way to define operators on interfaces. Unfortunately C# does not allow user-defined conversions to or from an interface so one have to explicitly wrap all instances of the interface in an expression that do not have wrapper on one side of an expression. While it can be acceptable in some cases (like Wrap(a) + b + c + d ...), it can make more complex expressions very cumbersome (like (Wrap(a) + b) + (Wrap(c) + d) ... hence it does not solve the problem that Ciprian described.
Max, thank you for writing back. That's an ingenious resolution to some of the problems you originally pointed out. Thank you!
As far as I can tell, this seems to strengthen the original argument, although there's still some corner cases, like the one pointed out by Ciprian. We can use Decorators as concrete dependencies as you point out, as an argument that even two (or n) identical polymorphic dependencies can be treated as though they were distinct dependencies.
What if we have an arbitrary number of dependencies? One example would be of a Composite, but it doesn't have to be. Consider the ShippingCostCalculatorFactory class from this example. It depends on a list of IBasketCalculator candidates. Could such a class, too, be refactored to an abstract class?
I suppose it could, since the dependency then really isn't an arbitrary number of IBasketCalculator, but rather the dependency is on a collection. Would it be enough to refactor to an abstract class with a single Factory Method that returns the candidates?
Mark, you're welcome! Admittedly, my solution is heavily inspired by the strong-typing as promoted by "if a Haskell program compiles, it probably works" and the original purpose of Hungarian notation.
As for an abrbitrary number of dependencies, you have already pointed out that the dependency is the collection itself, not its elements. So I think ShippingCostCalculatorFactory can be refactored to an abstract class with an abstract factory method to provide a collection of IBasketCalculator.
While abstract class would be more complex and less elegant than DI implementation, I find the reversibility of refactorings very important. Reversability means that the changes to the code are not changing the behavior of the compiled program. It allows to refactor even obscure and undertested legacy code without fear of breaking it. I find the two-way nature of changes to the code the most interesting about your concept of software isomorphisms.
I think the reason abstract classes are usually difficult to reason about and often considered to be a bad choice is that an abstract class and it's inheritors create an implicit composition and the relationships of the parts of this composition can be very different. A base class can serve as a collection of helper methods, or derived classes can serve as dependencies or specify dependencies like in the ShippingCostCalculatorFactory example, or inheitors can serve as a configuration to the base class like custom configuration element classes in .NET derived from ConfigurationElement. Abstract base class can be even used to implement disciminated unions (and in fact F# compiler does).
Perhaps different kinds of hierarchies can be enumerated with some formal ways to recognize a specific kind of hierarchy and refactor it into an explicit compistion?
P.S. One way to implement discriminated unions with C# abstract base classes and guarantee exhaustive matching:
public interface IOptionVisitor<T> { void Some(T value); void None(); } public abstract class Option<T> { private sealed class SomeImpl : Option<T> { private T _value; public SomeImpl(T value) { _value = value; } public override void AcceptVisitor(IOptionVisitor<T> visitor) { visitor.Some(_value); } } private sealed class NoneImpl : Option<T> { public override void AcceptVisitor(IOptionVisitor<T> visitor) { visitor.None(); } } private Option () { } public abstract void AcceptVisitor(IOptionVisitor<T> visitor); public static Option<T> Some(T value) { return new SomeImpl(value); } public static Option<T> None { get; } = new NoneImpl(); }
While I don't see how this kind of abstract base class can be refactored to DI, I can not call this a constraint on the abstact class isomorphism because semantically it is not an asbtract class in first place.
Max, once again thank you for writing. I've never seen that article by Joel Spolsky before, but I particularly liked your enumeration of the various different roles an abstract class can have.
It's seems that we're generally in agreement about the constraints of the described refactoring.
When it comes to your option implementation, I think you could fairly easy split up Option<T> into an interface that defines the AcceptVisitor method, and two classes that implements that interface. This is, however, closely related to a series of articles I'll publish in the future.
Mark, thank you for pointing out the alternative option implementation.
The key trick in my Option implementation is the use of private constructor in an abstract class with nested sealed implementation classes. Nested classes can access the private contructor while any class "outside" Option would be unable to call the base constructor. Now I think that enforcing that there are no implementation of Option except for SomeImpl and NoneImpl is redundant as long as the implementations are correct.
Perhaps I should have made an example with public nested classes which can be matched by their type but then it could be refactored into Visitor pattern too. Does it mean that Visitor is isomorphic to discriminated unions then?
Max, I agree that using a nested, private, sealed class is a good way to ensure that no-one else can add rogue implementations of an interface like IOptionVisitor<T>.
Additionally, I think that you're correct that it isn't possible to lock down the API to the same degree if you redefine Option<T> to an interface. Just to be clear, I'm thinking about something like this:
public interface IOptionVisitor<T> { void Some(T value); void None(); } public interface IOption<T> { void AcceptVisitor(IOptionVisitor<T> visitor); } public static class Option { public static IOption<T> Some<T>(T value) { return new SomeImpl<T>(value); } private sealed class SomeImpl<T> : IOption<T> { private T value; public SomeImpl(T value) { this.value = value; } public void AcceptVisitor(IOptionVisitor<T> visitor) { visitor.Some(value); } } public static IOption<T> None<T>() { return new NoneImpl<T>(); } private sealed class NoneImpl<T> : IOption<T> { public void AcceptVisitor(IOptionVisitor<T> visitor) { visitor.None(); } } }
With a design like that, rogue implementations of IOption<T> are possible, and I admit that I can't think of a way to prevent that.
Usually, that doesn't concern me that much, but if one were to publish a type like that as, say, a public NuGet package, that degree of lock-down could, in fact, be desirable. So, it looks like you've identified another constraint on the isomorphism. I admit that I may have been too focused on the ability to implement behaviour in various different ways, whereas I haven't given too much thought to accessibility.
To be frank, one of the reasons for that is that I tend to not consider accessibility modifiers too much in C#, as I tend to design classes in such a way that they protect their invariants. When classes do that, I'm happy to make most methods public.
Another reason that I've been vague on accessibility is that this could easily get implementation-specific. The way C#'s access modifiers work is different from Java's and C++'s.
That doesn't change the fact, though, that it looks like you've identified another constraint on the isomorphism, and for that I'm very grateful. Perhaps we ought to say something like:
Abstract classes are isomorphic with dependency injection up to accessibility.Again, there may be other constraints than that (and operator overloads), but I'm beholden to you for fleshing out those that you've already identified.
About the relationship between discriminated unions and the Visitor design pattern, then yes: those are isomorphic. That's a known property, but I'm going to publish a whole (sub-)series of articles about that particular topic in the future, so I think it'd be better to discuss that when we get there. I've already written those articles, but it'll take months before I publish them, according to the publishing schedule that I currently have in mind. Very prescient of you, though.

Comments
I've been struggling a bit with the terminology and I could use a bit of help.
I understand a
Monoid<a>to be of typea -> a -> a. I further understand that it can be said thata"forms a monoid over" the specifica -> a -> aimplementation. We can then say that an int forms two different monoids over addition and multiplication.Is my understanding above accurate and if so wouldn't it be more accurate to say that you can create a composite from an interface only when all of its methods return values that form monoids? Saying that they have to return monoids (instead of values that form them) goes against my understanding that a monoid is a binary operation.
Thanks a lot for an amazing article series, and for this blog overall. Keep up the good work!
Nikola, thank you for writing. You're correct: it would be more correct to say that you can create a Composite from an interface when all of its methods return types that form monoids. Throughout this article series, I've been struggling to keep my language as correct and specific as possible, but I sometimes slip up.
This has come up before, so perhaps you'll find this answer helpful.
By the way, there's one exception to the rule that in order to be able to create a Composite, all methods must return types that form monoids. This is when the return type is the same as the input type. The resulting Composite is still a monoid, so the overall conclusion holds.