ploeh blog danish software design
Das verflixte Hunde-Spiel
A puzzle kata, and a possible solution.
When I was a boy I had a nine-piece puzzle that I'd been gifted by the Swizz branch of my family. It's called Das verflixte Hunde-Spiel, which means something like the confounded dog game in English. And while a puzzle with nine pieces doesn't sound like much, it is, in fact, incredibly difficult.
It's just a specific incarnation of a kind of game that you've almost certainly encountered, too.

There are nine tiles, each with two dog heads and two dog ends. A dog may be coloured in one of four different patterns. The object of the game is to lay out the nine tiles in a 3x3 square so that all dog halves line up.
Game details #
The game is from 1979. Two of the tiles are identical, and, according to the information on the back of the box, two possible solutions exist. Described from top clockwise, the tiles are the following:
- Brown head, grey head, umber tail, spotted tail
- Brown head, spotted head, brown tail, umber tail
- Brown head, spotted head, grey tail, umber tail
- Brown head, spotted head, grey tail, umber tail
- Brown head, umber head, spotted tail, grey tail
- Grey head, brown head, spotted tail, umber tail
- Grey head, spotted head, brown tail, umber tail
- Grey head, umber head, brown tail, spotted tail
- Grey head, umber head, grey tail, spotted tail
I've taken the liberty of using a shorthand for the patterns. The grey dogs are actually also spotted, but since there's only one grey pattern, the grey label is unambiguous. The dogs I've named umber are actually rather burnt umber, but that's too verbose for my tastes, so I just named them umber. Finally, the label spotted indicates dogs that are actually burnt umber with brown blotches.
Notice that there are two tiles with a brown head, a spotted head, a grey tail, and an umber tail.
The object of the game is to lay down the tiles in a 3x3 square so that all dogs fit. For further reference, I've numbered each position from one to nine like this:

What makes the game hard? There are nine cards, so if you start with the upper left corner, you have nine choices. If you just randomly put down the tiles, you now have eight left for the top middle position, and so on. Standard combinatorics indicate that there are at least 9! = 362,880 permutations.
That's not the whole story, however, since you can rotate each tile in four different ways. You can rotate the first tile four ways, the second tile four ways, etc. for a total of 49 = 262,144 ways. Multiply these two numbers together, and you get 499! = 95,126,814,720 combinations. No wonder this puzzle is hard if there's only two solutions.
When analysed this way, however, there are actually 16 solutions, but that still makes it incredibly unlikely to arrive at a solution by chance. I'll get back to why there are 16 solutions later. For now, you should have enough information to try your hand with this game, if you'd like.
I found that the game made for an interesting kata: Write a program that finds all possible solutions to the puzzle.
If you'd like to try your hand at this exercise, I suggest that you pause reading here.
In the rest of the article, I'll outline my first attempt. Spoiler alert: I'll also show one of the solutions.
Types #
When you program in Haskell, it's natural to start by defining some types.
data Half = Head | Tail deriving (Show, Eq) data Pattern = Brown | Grey | Spotted | Umber deriving (Show, Eq) data Tile = Tile { top :: (Pattern, Half), right :: (Pattern, Half), bottom :: (Pattern, Half), left :: (Pattern, Half) } deriving (Show, Eq)
Each tile describes what you find on its top, right side, bottom, and left side.
We're also going to need a function to evaluate whether two halves match:
matches :: (Pattern, Half) -> (Pattern, Half) -> Bool matches (p1, h1) (p2, h2) = p1 == p2 && h1 /= h2
This function demands that the patterns match, but that the halves are opposites.
You can use the Tile type and its constituents to define the nine tiles of the game:
tiles :: [Tile] tiles = [ Tile (Brown, Head) (Grey, Head) (Umber, Tail) (Spotted, Tail), Tile (Brown, Head) (Spotted, Head) (Brown, Tail) (Umber, Tail), Tile (Brown, Head) (Spotted, Head) (Grey, Tail) (Umber, Tail), Tile (Brown, Head) (Spotted, Head) (Grey, Tail) (Umber, Tail), Tile (Brown, Head) (Umber, Head) (Spotted, Tail) (Grey, Tail), Tile (Grey, Head) (Brown, Head) (Spotted, Tail) (Umber, Tail), Tile (Grey, Head) (Spotted, Head) (Brown, Tail) (Umber, Tail), Tile (Grey, Head) (Umber, Head) (Brown, Tail) (Spotted, Tail), Tile (Grey, Head) (Umber, Head) (Grey, Tail) (Spotted, Tail) ]
Because I'm the neatnik that I am, I've sorted the tiles in lexicographic order, but the solution below doesn't rely on that.
Brute force doesn't work #
Before I started, I cast around the internet to see if there was an appropriate algorithm for the problem. While I found a few answers on Stack Overflow, none of them gave me indication that any sophisticated algorithm was available. (Even so, there may be, and I just didn't find it.)
It seems clear, however, that you can implement some kind of recursive search-tree algorithm that cuts a branch off as soon as it realizes that it doesn't work. I'll get back to that later, so let's leave that for now.
Since I'd planned on writing the code in Haskell, I decided to first try something that might look like brute force. Because Haskell is lazily evaluated, you can sometimes get away with techniques that look wasteful when you're used to strict/eager evaluation. In this case, it turned out to not work, but it's often quicker to just make the attempt than trying to analyze the problem.
As already outlined, I first attempted a purely brute-force solution, betting that Haskell's lazy evaluation would be enough to skip over the unnecessary calculations:
allRotationsOf9 = replicateM 9 [0..3] allRotations :: [Tile] -> [[Tile]] allRotations ts = fmap (\rs -> (\(r, t) -> rotations t !! r) <$> zip rs ts) allRotationsOf9 allConfigurations :: [[Tile]] allConfigurations = permutations tiles >>= allRotations solutions = filter isSolution allConfigurations
My idea with the allConfigurations value was that it's supposed to enumerate all 95 billion combinations. Whether it actually does that, I was never able to verify, because if I try to run that code, my poor laptop runs for a couple of hours before it eventually runs out of memory. In other words, the GHCi process crashes.
I haven't shown isSolution or rotations, because I consider the implementations irrelevant. This attempt doesn't work anyway.
Now that I look at it, it's quite clear why this isn't a good strategy. There's little to be gained from lazy evaluation when the final attempt just attempts to filter a list. Even with lazy evaluation, the code still has to run through all 95 billion combinations.
Things might have been different if I just had to find one solution. With a little luck, it might be that the first solution appears after, say, a hundred million iterations, and lazy evaluation would then had meant that the remaining combinations would never run. Not so here, but hindsight is 20-20.
Search tree #
Back to the search tree idea. It goes like this: Start from the top left position and pick a random tile and rotation. Now pick an arbitrary tile that fits and place it to the right of it, and so on. As far as I can tell, you can always place the first four cards, but from there, you can easily encounter a combination that allows no further tiles. Here's an example:

None of the remaining five tiles fit in the fifth position. This means that we don't have to do any permutations that involve these four tiles in that combination. While the algorithm has to search through all five remaining tiles and rotations to discover that none fit in position 5, once it knows that, it doesn't have to go through the remaining four positions. That's 444! = 6,144 combinations that it can skip every time it discovers an impossible beginning. That doesn't sound like that much, but if we assume that this happens more often than not, it's still an improvement by orders of magnitude.
We may think of this algorithm as constructing a search tree, but immediately pruning all branches that aren't viable, as close to the root as possible.
Matches #
Before we get to the algorithm proper we need a few simple helper functions. One kind of function is a predicate that determines if a particular tile can occupy a given position. Since we may place any tile in any rotation in the first position, we don't need to write a predicate for that, but if we wanted to generalize, const True would do.
Whether or not we can place a given tile in the second position depends exclusively on the tile in the first position:
tile2Matches :: Tile -> Tile -> Bool tile2Matches t1 t2 = right t1 `matches` left t2
If the right dog part of the first tile matches the left part of the second tile, the return value is True; otherwise, it's False. Note that I'm using infix notation for matches. I could also have written the function as
tile2Matches :: Tile -> Tile -> Bool tile2Matches t1 t2 = matches (right t1) (left t2)
but it doesn't read as well.
In any case, the corresponding matching functions for the third and forth tile look similar:
tile3Matches :: Tile -> Tile -> Bool tile3Matches t2 t3 = right t2 `matches` left t3 tile4Matches :: Tile -> Tile -> Bool tile4Matches t1 t4 = bottom t1 `matches` top t4
Notice that tile4Matches compares the fourth tile with the first tile rather than the third tile, because position 4 is directly beneath position 1, rather than to the right of position 3 (cf. the grid above). For that reason it also compares the bottom of tile 1 to the top of the fourth tile.
The matcher for the fifth tile is different:
tile5Matches :: Tile -> Tile -> Tile -> Bool tile5Matches t2 t4 t5 = bottom t2 `matches` top t5 && right t4 `matches` left t5
This is the first predicate that depends on two, rather than one, previous tiles. In position 5 we need to examine both the tile in position 2 and the one in position 4.
The same is true for position 6:
tile6Matches :: Tile -> Tile -> Tile -> Bool tile6Matches t3 t5 t6 = bottom t3 `matches` top t6 && right t5 `matches` left t6
but then the matcher for position 7 looks like the predicate for position 4:
tile7Matches :: Tile -> Tile -> Bool tile7Matches t4 t7 = bottom t4 `matches` top t7
This is, of course, because the tile in position 7 only has to consider the tile in position 4. Finally, not surprising, the two remaining predicates look like something we've already seen:
tile8Matches :: Tile -> Tile -> Tile -> Bool tile8Matches t5 t7 t8 = bottom t5 `matches` top t8 && right t7 `matches` left t8 tile9Matches :: Tile -> Tile -> Tile -> Bool tile9Matches t6 t8 t9 = bottom t6 `matches` top t9 && right t8 `matches` left t9
You may suggest that it'd be possible to reduce the number of predicates. After all, there's effectively only three different predicates: One that only looks at the tile to the left, one that only looks at the tile above, and one that looks both to the left and above.
Indeed, I could have boiled it down to just three functions:
matchesHorizontally :: Tile -> Tile -> Bool matchesHorizontally x y = right x `matches` left y matchesVertically :: Tile -> Tile -> Bool matchesVertically x y = bottom x `matches` top y matchesBoth :: Tile -> Tile -> Tile -> Bool matchesBoth x y z = matchesVertically x z && matchesHorizontally y z
but I now run the risk of calling the wrong predicate from my implementation of the algorithm. As you'll see, I'll call each predicate by name at each appropriate step, but if I had only these three functions, there's a risk that I might mistakenly use matchesHorizontally when I should have used matchesVertically, or vice versa. Reducing eight one-liners to three one-liners doesn't really seem to warrant the risk.
Rotations #
In addition to examining whether a given tile fits in a given position, we also need to be able to rotate any tile:
rotateClockwise :: Tile -> Tile rotateClockwise (Tile t r b l) = Tile l t r b rotateCounterClockwise :: Tile -> Tile rotateCounterClockwise (Tile t r b l) = Tile r b l t upend :: Tile -> Tile upend (Tile t r b l) = Tile b l t r
What is really needed, it turns out, is to enumerate all four rotations of a tile:
rotations :: Tile -> [Tile] rotations t = [t, rotateClockwise t, upend t, rotateCounterClockwise t]
Since this, like everything else here, is a pure function, I experimented with defining a 'memoized tile' type that embedded all four rotations upon creation, so that the algorithm doesn't need to call the rotations function millions of times, but I couldn't measure any discernable performance improvement from it. There's no reason to make things more complicated than they need to be, so I didn't keep that change. (Since I do, however, use Git tactically i did, of course, stash the experiment.)
Permutations #
While I couldn't make things work by enumerating all 95 billion combinations, enumerating all 362,880 permutations of non-rotated tiles is well within the realm of the possible:
allPermutations :: [(Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile)] allPermutations = (\[t1, t2, t3, t4, t5, t6, t7, t8, t9] -> (t1, t2, t3, t4, t5, t6, t7, t8, t9)) <$> permutations tiles
Doing this in GHCi on my old laptop takes 300 milliseconds, which is good enough compared to what comes next.
This list value uses permutations to enumerate all the permutations. You may already have noticed that it converts the result into a nine-tuple. The reason for that is that this enables the algorithm to pattern-match into specific positions without having to resort to the index operator, which is both partial and requires iteration of the list to reach the indexed element. Granted, the list is only nine elements long, and often the algorithm will only need to index to the fourth or fifth element. On the other hand, it's going to do it a lot. Perhaps it's a premature optimization, but if it is, it's at least one that makes the code more, rather than less, readable.
Algorithm #
I found it easiest to begin at the 'bottom' of what is effectively a recursive algorithm, even though I didn't implement it that way. At the 'bottom', I imagine that I'm almost done: That I've found eight tiles that match, and now I only need to examine if I can rotate the final tile so that it matches:
solve9th :: (a, b, c, d, e, Tile, g, Tile, Tile) -> [(a, b, c, d, e, Tile, g, Tile, Tile)] solve9th (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- filter (tile9Matches t6 t8) $ rotations t9 return (t1, t2, t3, t4, t5, t6, t7, t8, match)
Recalling that Haskell functions compose from right to left, the function starts by enumerating the four rotations of the ninth and final tile t9. It then filters those four rotations by the tile9Matches predicate.
The match value is a rotation of t9 that matches t6 and t8. Whenever solve9th finds such a match, it returns the entire nine-tuple, because the assumption is that the eight first tiles are already valid.
Notice that the function uses do notation in the list monad, so it's quite possible that the first filter expression produces no match. In that case, the second line of code never runs, and instead, the function returns the empty list.
How do we find a tuple where the first eight elements are valid? Well, if we have seven valid tiles, we may consider the eighth and subsequently call solve9th:
solve8th :: (a, b, c, d, Tile, Tile, Tile, Tile, Tile) -> [(a, b, c, d, Tile, Tile, Tile, Tile, Tile)] solve8th (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- filter (tile8Matches t5 t7) $ rotations t8 solve9th (t1, t2, t3, t4, t5, t6, t7, match, t9)
This function looks a lot like solve9th, but it instead enumerates the four rotations of the eighth tile t8 and filters with the tile8Matches predicate. Due to the do notation, it'll only call solve9th if it finds a match.
Once more, this function assumes that the first seven tiles are already in a legal constellation. How do we find seven valid tiles? The same way we find eight: By assuming that we have six valid tiles, and then finding the seventh, and so on:
solve7th :: (a, b, c, Tile, Tile, Tile, Tile, Tile, Tile) -> [(a, b, c, Tile, Tile, Tile, Tile, Tile, Tile)] solve7th (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- filter (tile7Matches t4) $ rotations t7 solve8th (t1, t2, t3, t4, t5, t6, match, t8, t9) solve6th :: (a, b, Tile, Tile, Tile, Tile, Tile, Tile, Tile) -> [(a, b, Tile, Tile, Tile, Tile, Tile, Tile, Tile)] solve6th (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- filter (tile6Matches t3 t5) $ rotations t6 solve7th (t1, t2, t3, t4, t5, match, t7, t8, t9) solve5th :: (a, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile) -> [(a, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile)] solve5th (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- filter (tile5Matches t2 t4) $ rotations t5 solve6th (t1, t2, t3, t4, match, t6, t7, t8, t9) solve4th :: (Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile) -> [(Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile)] solve4th (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- filter (tile4Matches t1) $ rotations t4 solve5th (t1, t2, t3, match, t5, t6, t7, t8, t9) solve3rd :: (Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile) -> [(Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile)] solve3rd (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- filter (tile3Matches t2) $ rotations t3 solve4th (t1, t2, match, t4, t5, t6, t7, t8, t9) solve2nd :: (Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile) -> [(Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile)] solve2nd (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- filter (tile2Matches t1) $ rotations t2 solve3rd (t1, match, t3, t4, t5, t6, t7, t8, t9)
You'll observe that solve7th down to solve2nd are very similar. The only things that really vary are the predicates, and the positions of the tile being examined, as well as its neighbours. Clearly I can generalize this code, but I'm not sure it's worth it. I wrote a few of these in the order I've presented them here, because it helped me think the problem through, and to be honest, once I had two or three of them, GitHub Copilot picked up on the pattern and wrote the remaining functions for me.
Granted, typing isn't a programming bottleneck, so we should rather ask if this kind of duplication looks like a maintenance problem. Given that this is a one-time exercise, I'll just leave it be and move on.
Particularly, if you're struggling to understand how this implements the 'truncated search tree', keep in mind that e..g solve5th is likely to produce no valid match, in which case it'll never call solve6th. The same may happen in solve6th, etc.
The 'top' function is a bit different because it doesn't need to filter anything:
solve1st :: (Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile) -> [(Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile)] solve1st (t1, t2, t3, t4, t5, t6, t7, t8, t9) = do match <- rotations t1 solve2nd (match, t2, t3, t4, t5, t6, t7, t8, t9)
In the first position, any tile in any rotation is legal, so solve1st only enumerates all four rotations of t1 and calls solve2nd for each.
The final step is to compose allPermutations with solve1st:
solutions :: [(Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile, Tile)] solutions = allPermutations >>= solve1st
Running this in GHCi on my 4½-year old laptop produces all 16 solutions in approximately 22 seconds.
Evaluation #
Is that good performance? Well, it turns out that it's possible to substantially improve on the situation. As I've mentioned a couple of times, so far I've been running the program from GHCi, the Haskell REPL. Most of the 22 seconds are spent interpreting or compiling the code.
If I compile the code with some optimizations turned on, the executable runs in approximately 300 ms. That seems quite decent, if I may say so.
I can think of a few tweaks to the code that might conceivably improve things even more, but when I test, there's no discernable difference. Thus, I'll keep the code as shown here.
Here's one of the solutions:

The information on the box claims that there's two solutions. Why does the code shown here produce 16 solutions?
There's a good explanation for that. Recall that two of the tiles are identical. In the above solution picture, it's tile 1 and 3, although they're rotated 90° in relation to each other. This implies that you could take tile 1, rotate it counter-clockwise and put it in position 3, while simultaneously taking tile 3, rotating it clockwise, and putting it in position 1. Visually, you can't tell the difference, so they don't count as two distinct solutions. The algorithm, however, doesn't make that distinction, so it enumerates what is effectively the same solution twice.
Not surprising, it turns out that all 16 solutions are doublets in that way. We can confirm that by evaluating length $ nub solutions, which returns 8.
Eight solutions are, however, still four times more than two. Can you figure out what's going on?
The algorithm also enumerates four rotations of each solution. Once we take this into account, there's only two visually distinct solutions left. One of them is shown above. I also have a picture of the other one, but I'm not going to totally spoil things for you.
Conclusion #
When I was eight, I might have had the time and the patience to actually lay the puzzle. Despite the incredibly bad odds, I vaguely remember finally solving it. There must be some more holistic processing going on in the brain, if even a kid can solve the puzzle, because it seems inconceivable that it should be done as described here.
Today, I don't care for that kind of puzzle in analog form, but I did, on the other hand, find it an interesting programming exercise.
The code could be smaller, but I like it as it is. While a bit on the verbose side, I think that it communicates well what's going on.
I was pleasantly surprised that I managed to get execution time down to 300 ms. I'd honestly not expected that when I started.
FSZipper in C#
Another functional model of a file system, with code examples in C#.
This article is part of a series about Zippers. In this one, I port the FSZipper data structure from the Learn You a Haskell for Great Good! article Zippers.
A word of warning: I'm assuming that you're familiar with the contents of that article, so I'll skip the pedagogical explanations; I can hardly do it better that it's done there. Additionally, I'll make heavy use of certain standard constructs to port Haskell code, most notably Church encoding to model sum types in languages that don't natively have them. Such as C#. In some cases, I'll implement the Church encoding using the data structure's catamorphism. Since the cyclomatic complexity of the resulting code is quite low, you may be able to follow what's going on even if you don't know what Church encoding or catamorphisms are, but if you want to understand the background and motivation for that style of programming, you can consult the cited resources.
The code shown in this article is available on GitHub.
File system item initialization and structure #
If you haven't already noticed, Haskell (and other statically typed functional programming languages like F#) makes heavy use of sum types, and the FSZipper example is no exception. It starts with a one-liner to define a file system item, which may be either a file or a folder. In C# we must instead use a class:
public sealed class FSItem
Contrary to the two previous examples, the FSItem class has no generic type parameter. This is because I'm following the Haskell example code as closely as possible, but as I've previously shown, you can model a file hierarchy with a general-purpose rose tree.
Staying consistent with the two previous articles, I'll use Church encoding to model a sum type, and as discussed in the previous article I use a private implementation for that.
private readonly IFSItem imp; private FSItem(IFSItem imp) { this.imp = imp; } public static FSItem CreateFile(string name, string data) { return new(new File(name, data)); } public static FSItem CreateFolder(string name, IReadOnlyCollection<FSItem> items) { return new(new Folder(name, items)); }
Two static creation methods enable client developers to create a single FSItem object, or an entire tree, like the example from the Haskell code, here ported to C#:
private static readonly FSItem myDisk = FSItem.CreateFolder("root", [ FSItem.CreateFile("goat_yelling_like_man.wmv", "baaaaaa"), FSItem.CreateFile("pope_time.avi", "god bless"), FSItem.CreateFolder("pics", [ FSItem.CreateFile("ape_throwing_up.jpg", "bleargh"), FSItem.CreateFile("watermelon_smash.gif", "smash!!"), FSItem.CreateFile("skull_man(scary).bmp", "Yikes!") ]), FSItem.CreateFile("dijon_poupon.doc", "best mustard"), FSItem.CreateFolder("programs", [ FSItem.CreateFile("fartwizard.exe", "10gotofart"), FSItem.CreateFile("owl_bandit.dmg", "mov eax, h00t"), FSItem.CreateFile("not_a_virus.exe", "really not a virus"), FSItem.CreateFolder("source code", [ FSItem.CreateFile("best_hs_prog.hs", "main = print (fix error)"), FSItem.CreateFile("random.hs", "main = print 4") ]) ]) ]);
Since the imp class field is just a private implementation detail, a client developer needs a way to query an FSItem object about its contents.
File system item catamorphism #
Just like the previous article, I'll start with the catamorphism. This is essentially the rose tree catamorphism, just less generic, since FSItem doesn't have a generic type parameter.
public TResult Aggregate<TResult>( Func<string, string, TResult> whenFile, Func<string, IReadOnlyCollection<TResult>, TResult> whenFolder) { return imp.Aggregate(whenFile, whenFolder); }
The Aggregate method delegates to its internal implementation class field, which is defined as the private nested interface IFSItem:
private interface IFSItem { TResult Aggregate<TResult>( Func<string, string, TResult> whenFile, Func<string, IReadOnlyCollection<TResult>, TResult> whenFolder); }
As discussed in the previous article, the interface is hidden away because it's only a vehicle for polymorphism. It's not intended for client developers to be used (although that would be benign) or implemented (which could break encapsulation). There are only, and should ever only be, two implementations. The one that represents a file is the simplest:
private sealed record File(string Name, string Data) : IFSItem { public TResult Aggregate<TResult>( Func<string, string, TResult> whenFile, Func<string, IReadOnlyCollection<TResult>, TResult> whenFolder) { return whenFile(Name, Data); } }
The File record's Aggregate method unconditionally calls the supplied whenFile function argument with the Name and Data that was originally supplied via its constructor.
The Folder implementation is a bit trickier, mostly due to its recursive nature, but also because I wanted it to have structural equality.
private sealed class Folder : IFSItem { private readonly string name; private readonly IReadOnlyCollection<FSItem> items; public Folder(string Name, IReadOnlyCollection<FSItem> Items) { name = Name; items = Items; } public TResult Aggregate<TResult>( Func<string, string, TResult> whenFile, Func<string, IReadOnlyCollection<TResult>, TResult> whenFolder) { return whenFolder( name, items.Select(i => i.Aggregate(whenFile, whenFolder)).ToList()); } public override bool Equals(object? obj) { return obj is Folder folder && name == folder.name && items.SequenceEqual(folder.items); } public override int GetHashCode() { return HashCode.Combine(name, items); } }
It, too, unconditionally calls one of the two functions passed to its Aggregate method, but this time whenFolder. It does that, however, by first recursively calling Aggregate within a Select expression. It needs to do that because the whenFolder function expects the subtree to have been already converted to values of the TResult return type. This is a common pattern with catamorphisms, and takes a bit of time getting used to. You can see similar examples in the articles Tree catamorphism, Rose tree catamorphism, Full binary tree catamorphism, as well as the previous one in this series.
I also had to make Folder a class rather than a record, because I wanted the type to have structural equality, and you can't override Equals on records (and if the base class library has any collection type with structural equality, I'm not aware of it).
File system item Church encoding #
True to the structure of the previous article, the catamorphism doesn't look quite like a Church encoding, but it's possible to define the latter from the former.
public TResult Match<TResult>( Func<string, string, TResult> whenFile, Func<string, IReadOnlyCollection<FSItem>, TResult> whenFolder) { return Aggregate( whenFile: (name, data) => (item: CreateFile(name, data), result: whenFile(name, data)), whenFolder: (name, pairs) => { var items = pairs.Select(i => i.item).ToList(); return (CreateFolder(name, items), whenFolder(name, items)); }).result; }
The trick is the same as in the previous article: Build up an intermediate tuple that contains both the current item as well as the result being accumulated. Once the Aggregate method returns, the Match method returns only the result part of the resulting tuple.
I implemented the whenFolder expression as a code block, because both tuple elements needed the items collection. You can inline the Select expression, but that would cause it to run twice. That's probably a premature optimization, but it also made the code a bit shorter, and, one may hope, a bit more readable.
Fily system breadcrumb #
Finally, things seem to be becoming a little easier. The port of FSCrumb is straightforward.
public sealed class FSCrumb { public FSCrumb( string name, IReadOnlyCollection<FSItem> left, IReadOnlyCollection<FSItem> right) { Name = name; Left = left; Right = right; } public string Name { get; } public IReadOnlyCollection<FSItem> Left { get; } public IReadOnlyCollection<FSItem> Right { get; } public override bool Equals(object? obj) { return obj is FSCrumb crumb && Name == crumb.Name && Left.SequenceEqual(crumb.Left) && Right.SequenceEqual(crumb.Right); } public override int GetHashCode() { return HashCode.Combine(Name, Left, Right); } }
The only reason this isn't a record is, once again, that I want to override Equals so that the type can have structural equality. Visual Studio wants me to convert to a primary constructor. That would simplify the code a bit, but actually not that much.
(I'm still somewhat conservative in my choice of new C# language features. Not that I have anything against primary constructors which, after all, F# has had forever. The reason I'm holding back is for didactic reasons. Not every reader is on the latest language version, and some readers may be using another programming language entirely. On the other hand, primary constructors seem natural and intuitive, so I may start using them here on the blog as well. I don't think that they're going to be much of a barrier to understanding.)
Now that we have both the data type we want to zip, as well as the breadcrumb type we need, we can proceed to add the Zipper.
File system Zipper #
The FSZipper C# class fills the position of the eponymous Haskell type alias. Data structure and initialization is straightforward.
public sealed class FSZipper { private FSZipper(FSItem fSItem, IReadOnlyCollection<FSCrumb> breadcrumbs) { FSItem = fSItem; Breadcrumbs = breadcrumbs; } public FSZipper(FSItem fSItem) : this(fSItem, []) { } public FSItem FSItem { get; } public IReadOnlyCollection<FSCrumb> Breadcrumbs { get; } // Methods follow here...
True to the style I've already established, I've made the master constructor private in order to highlight that the Breadcrumbs are the responsibility of the FSZipper class itself. It's not something client code need worry about.
Going down #
The Haskell Zippers article introduces fsUp before fsTo, but if we want to see some example code, we need to navigate to somewhere before we can navigate up. Thus, I'll instead start with the function that navigates to a child node.
public FSZipper? GoTo(string name) { return FSItem.Match( (_, _) => null, (folderName, items) => { FSItem? item = null; var ls = new List<FSItem>(); var rs = new List<FSItem>(); foreach (var i in items) { if (item is null && i.IsNamed(name)) item = i; else if (item is null) ls.Add(i); else rs.Add(i); } if (item is null) return null; return new FSZipper( item, Breadcrumbs.Prepend(new FSCrumb(folderName, ls, rs)).ToList()); }); }
This is by far the most complicated navigation we've seen so far, and I've even taken the liberty of writing an imperative implementation. It's not that I don't know how I could implement it in a purely functional fashion, but I've chosen this implementation for a couple of reasons. The first of which is that, frankly, it was easier this way.
This stems from the second reason: That the .NET base class library, as far as I know, offers no functionality like Haskell's break function. I could have written such a function myself, but felt that it was too much of a digression, even for me. Maybe I'll do that another day. It might make for a nice little exercise.
The third reason is that C# doesn't afford pattern matching on sequences, in the shape of destructuring the head and the tail of a list. (Not that I know of, anyway, but that language changes rapidly at the moment, and it does have some pattern-matching features now.) This means that I have to check item for null anyway.
In any case, while the implementation is imperative, an external caller can't tell. The GoTo method is still referentially transparent. Which means that it fits in your head.
You may have noticed that the implementation calls IsNamed, which is also new.
public bool IsNamed(string name) { return Match((n, _) => n == name, (n, _) => n == name); }
This is an instance method I added to FSItem.
In summary, the GoTo method enables client code to navigate down in the file hierarchy, as this unit test demonstrates:
[Fact] public void GoToSkullMan() { var sut = new FSZipper(myDisk); var actual = sut.GoTo("pics")?.GoTo("skull_man(scary).bmp"); Assert.NotNull(actual); Assert.Equal( FSItem.CreateFile("skull_man(scary).bmp", "Yikes!"), actual.FSItem); }
The example is elementary. First go to the pics folder, and from there to the skull_man(scary).bmp.
Going up #
Going back up the hierarchy isn't as complicated.
public FSZipper? GoUp() { if (Breadcrumbs.Count == 0) return null; var head = Breadcrumbs.First(); var tail = Breadcrumbs.Skip(1); return new FSZipper( FSItem.CreateFolder(head.Name, [.. head.Left, FSItem, .. head.Right]), tail.ToList()); }
If the Breadcrumbs collection is empty, we're already at the root, in which case we can't go further up. In that case, the GoUp method returns null, as does the GoTo method if it can't find an item with the desired name. This possibility is explicitly indicated by the FSZipper? return type; notice the question mark, which indicates that the value may be null. If you're working in a context or language where that feature isn't available, you may instead consider taking advantage of the Maybe monad (which is also what you'd idiomatically do in Haskell).
If Breadcrumbs is not empty, it means that there's a place to go up to. It also implies that the previous operation navigated down, and the only way that's possible is if the previous node was a folder. Thus, the GoUp method knows that it needs to reconstitute a folder, and from the head breadcrumb, it knows that folder's name, and what was originally to the Left and Right of the Zipper's FSItem property.
This unit test demonstrates how client code may use the GoUp method:
[Fact] public void GoUpFromSkullMan() { var sut = new FSZipper(myDisk); // This is the same as the GoToSkullMan test var newFocus = sut.GoTo("pics")?.GoTo("skull_man(scary).bmp"); var actual = newFocus?.GoUp()?.GoTo("watermelon_smash.gif"); Assert.NotNull(actual); Assert.Equal( FSItem.CreateFile("watermelon_smash.gif", "smash!!"), actual.FSItem); }
This test first repeats the navigation also performed by the other test, then uses GoUp to go one level up, which finally enables it to navigate to the watermelon_smash.gif file.
Renaming a file or folder #
A Zipper enables you to navigate a data structure, but you can also use it to modify the element in focus. One option is to rename a file or folder.
public FSZipper Rename(string newName) { return new FSZipper( FSItem.Match( (_, dat) => FSItem.CreateFile(newName, dat), (_, items) => FSItem.CreateFolder(newName, items)), Breadcrumbs); }
The Rename method 'pattern-matches' on the 'current' FSItem and in both cases creates a new file or folder with the new name. Since it doesn't need the old name for anything, it uses the wildcard pattern to ignore that value. This operation is always possible, so the return type is FSZipper, without a question mark, indicating that the method never returns null.
The following unit test replicates the Haskell article's example by renaming the pics folder to cspi.
[Fact] public void RenamePics() { var sut = new FSZipper(myDisk); var actual = sut.GoTo("pics")?.Rename("cspi").GoUp(); Assert.NotNull(actual); Assert.Empty(actual.Breadcrumbs); Assert.Equal( FSItem.CreateFolder("root", [ FSItem.CreateFile("goat_yelling_like_man.wmv", "baaaaaa"), FSItem.CreateFile("pope_time.avi", "god bless"), FSItem.CreateFolder("cspi", [ FSItem.CreateFile("ape_throwing_up.jpg", "bleargh"), FSItem.CreateFile("watermelon_smash.gif", "smash!!"), FSItem.CreateFile("skull_man(scary).bmp", "Yikes!") ]), FSItem.CreateFile("dijon_poupon.doc", "best mustard"), FSItem.CreateFolder("programs", [ FSItem.CreateFile("fartwizard.exe", "10gotofart"), FSItem.CreateFile("owl_bandit.dmg", "mov eax, h00t"), FSItem.CreateFile("not_a_virus.exe", "really not a virus"), FSItem.CreateFolder("source code", [ FSItem.CreateFile("best_hs_prog.hs", "main = print (fix error)"), FSItem.CreateFile("random.hs", "main = print 4") ]) ]) ]), actual.FSItem); }
Since the test uses GoUp after Rename, the actual value contains the entire tree, while the Breadcrumbs collection is empty.
Adding a new file #
Finally, we can add a new file to a folder.
public FSZipper? Add(FSItem item) { return FSItem.Match<FSZipper?>( whenFile: (_, _) => null, whenFolder: (name, items) => new FSZipper( FSItem.CreateFolder(name, items.Prepend(item).ToList()), Breadcrumbs)); }
This operation may fail, since we can't add a file to a file. This is, again, clearly indicated by the return type, which allows null.
This implementation adds the file to the start of the folder, but it would also be possible to add it at the end. I would consider that slightly more idiomatic in C#, but here I've followed the Haskell example code, which conses the new item to the beginning of the list. As is idiomatic in Haskell.
The following unit test reproduces the Haskell article's example.
[Fact] public void AddPic() { var sut = new FSZipper(myDisk); var actual = sut.GoTo("pics")?.Add(FSItem.CreateFile("heh.jpg", "lol"))?.GoUp(); Assert.NotNull(actual); Assert.Equal( FSItem.CreateFolder("root", [ FSItem.CreateFile("goat_yelling_like_man.wmv", "baaaaaa"), FSItem.CreateFile("pope_time.avi", "god bless"), FSItem.CreateFolder("pics", [ FSItem.CreateFile("heh.jpg", "lol"), FSItem.CreateFile("ape_throwing_up.jpg", "bleargh"), FSItem.CreateFile("watermelon_smash.gif", "smash!!"), FSItem.CreateFile("skull_man(scary).bmp", "Yikes!") ]), FSItem.CreateFile("dijon_poupon.doc", "best mustard"), FSItem.CreateFolder("programs", [ FSItem.CreateFile("fartwizard.exe", "10gotofart"), FSItem.CreateFile("owl_bandit.dmg", "mov eax, h00t"), FSItem.CreateFile("not_a_virus.exe", "really not a virus"), FSItem.CreateFolder("source code", [ FSItem.CreateFile("best_hs_prog.hs", "main = print (fix error)"), FSItem.CreateFile("random.hs", "main = print 4") ]) ]) ]), actual.FSItem); Assert.Empty(actual.Breadcrumbs); }
This example also follows the edit with a GoUp call, with the effect that the Zipper is once more focused on the entire tree. The assertion verifies that the new heh.jpg file is the first file in the pics folder.
Conclusion #
The code for FSZipper is actually a bit simpler than for the binary tree. This, I think, is mostly attributable to the FSZipper having fewer constituent sum types. While sum types are trivial, and extraordinarily useful in languages that natively support them, they require a lot of boilerplate in a language like C#.
Do you need something like FSZipper in C#? Probably not. As I've already discussed, this article series mostly exists as a programming exercise.
Functor products
A tuple or class of functors is also a functor. An article for object-oriented developers.
This article is part of a series of articles about functor relationships. In this one you'll learn about a universal composition of functors. In short, if you have a product type of functors, that data structure itself gives rise to a functor.
Together with other articles in this series, this result can help you answer questions such as: Does this data structure form a functor?
Since functors tend to be quite common, and since they're useful enough that many programming languages have special support or syntax for them, the ability to recognize a potential functor can be useful. Given a type like Foo<T> (C# syntax) or Bar<T1, T2>, being able to recognize it as a functor can come in handy. One scenario is if you yourself have just defined such a data type. Recognizing that it's a functor strongly suggests that you should give it a Select method in C#, a map function in F#, and so on.
Not all generic types give rise to a (covariant) functor. Some are rather contravariant functors, and some are invariant.
If, on the other hand, you have a data type which is a product of two or more (covariant) functors with the same type parameter, then the data type itself gives rise to a functor. You'll see some examples in this article.
Abstract shape #
Before we look at some examples found in other code, it helps if we know what we're looking for. Most (if not all?) languages support product types. In canonical form, they're just tuples of values, but in an object-oriented language like C#, such types are typically classes.
Imagine that you have two functors F and G, and you're now considering a data structure that contains a value of both types.
public sealed class FAndG<T> { public FAndG(F<T> f, G<T> g) { F = f; G = g; } public F<T> F { get; } public G<T> G { get; } // Methods go here...
The name of the type is FAndG<T> because it contains both an F<T> object and a G<T> object.
Notice that it's an essential requirement that the individual functors (here F and G) are parametrized by the same type parameter (here T). If your data structure contains F<T1> and G<T2>, the following 'theorem' doesn't apply.
The point of this article is that such an FAndG<T> data structure forms a functor. The Select implementation is quite unsurprising:
public FAndG<TResult> Select<TResult>(Func<T, TResult> selector) { return new FAndG<TResult>(F.Select(selector), G.Select(selector)); }
Since we've assumed that both F and G already are functors, they must come with some projection function. In C# it's idiomatically called Select, while in F# it'd typically be called map:
// ('a -> 'b) -> FAndG<'a> -> FAndG<'b> let map f fandg = { F = F.map f fandg.F; G = G.map f fandg.G }
assuming a record type like
type FAndG<'a> = { F : F<'a>; G : G<'a> }
In both the C# Select example and the F# map function, the composed functor passes the function argument (selector or f) to both F and G and uses it to map both constituents. It then composes a new product from these individual results.
I'll have more to say about how this generalizes to a product of more than two functors, but first, let's consider some examples.
List Zipper #
One of the simplest example I can think of is a List Zipper, which in Haskell is nothing but a type alias of a tuple of lists:
type ListZipper a = ([a],[a])
In the article A List Zipper in C# you saw how the ListZipper<T> class composes two IEnumerable<T> objects.
private readonly IEnumerable<T> values; public IEnumerable<T> Breadcrumbs { get; } private ListZipper(IEnumerable<T> values, IEnumerable<T> breadcrumbs) { this.values = values; Breadcrumbs = breadcrumbs; }
Since we already know that sequences like IEnumerable<T> form functors, we now know that so must ListZipper<T>. And indeed, the Select implementation looks similar to the above 'shape outline'.
public ListZipper<TResult> Select<TResult>(Func<T, TResult> selector) { return new ListZipper<TResult>(values.Select(selector), Breadcrumbs.Select(selector)); }
It passes the selector function to the Select method of both values and Breadcrumbs, and composes the results into a new ListZipper<TResult>.
While this example is straightforward, it may not be the most compelling, because ListZipper<T> composes two identical functors: IEnumerable<T>. The knowledge that functors compose is more general than that.
Non-empty collection #
Next after the above List Zipper, the simplest example I can think of is a non-empty list. On this blog I originally introduced it in the article Semigroups accumulate, but here I'll use the variant from NonEmpty catamorphism. It composes a single value of the type T with an IReadOnlyCollection<T>.
public NonEmptyCollection(T head, params T[] tail) { if (head == null) throw new ArgumentNullException(nameof(head)); this.Head = head; this.Tail = tail; } public T Head { get; } public IReadOnlyCollection<T> Tail { get; }
The Tail, being an IReadOnlyCollection<T>, easily forms a functor, since it's a kind of list. But what about Head, which is a 'naked' T value? Does that form a functor? If so, which one?
Indeed, a 'naked' T value is isomorphic to the Identity functor. This situation is an example of how knowing about the Identity functor is useful, even if you never actually write code that uses it. Once you realize that T is equivalent with a functor, you've now established that NonEmptyCollection<T> composes two functors. Therefore, it must itself form a functor, and you realize that you can give it a Select method.
public NonEmptyCollection<TResult> Select<TResult>(Func<T, TResult> selector) { return new NonEmptyCollection<TResult>(selector(Head), Tail.Select(selector).ToArray()); }
Notice that even though we understand that T is equivalent to the Identity functor, there's no reason to actually wrap Head in an Identity<T> container just to call Select on it and unwrap the result. Rather, the above Select implementation directly invokes selector with Head. It is, after all, a function that takes a T value as input and returns a TResult object as output.
Ranges #
It's hard to come up with an example that's both somewhat compelling and realistic, and at the same time prototypically pure. Stripped of all 'noise' functor products are just tuples, but that hardly makes for a compelling example. On the other hand, most other examples I can think of combine results about functors where they compose in more than one way. Not only as products, but also as sums of functors, as well as nested compositions. You'll be able to read about these in future articles, but for the next examples, you'll have to accept some claims about functors at face value.
In Range as a functor you saw how both Endpoint<T> and Range<T> are functors. The article shows functor implementations for each, in both C#, F#, and Haskell. For now we'll ignore the deeper underlying reason why Endpoint<T> forms a functor, and instead focus on Range<T>.
In Haskell I never defined an explicit Range type, but rather just treated ranges as tuples. As stated repeatedly already, tuples are the essential products, so if you accept that Endpoint gives rise to a functor, then a 'range tuple' does, too.
In F# Range is defined like this:
type Range<'a> = { LowerBound : Endpoint<'a>; UpperBound : Endpoint<'a> }
Such a record type is also easily identified as a product type. In a sense, we can think of a record type as a 'tuple with metadata', where the metadata contains names of elements.
In C# Range<T> is a class with two Endpoint<T> fields.
private readonly Endpoint<T> min; private readonly Endpoint<T> max; public Range(Endpoint<T> min, Endpoint<T> max) { this.min = min; this.max = max; }
In a sense, you can think of such an immutable class as equivalent to a record type, only requiring substantial ceremony. The point is that because a range is a product of two functors, it itself gives rise to a functor. You can see all the implementations in Range as a functor.
Binary tree Zipper #
In A Binary Tree Zipper in C# you saw that the BinaryTreeZipper<T> class has two class fields:
public BinaryTree<T> Tree { get; } public IEnumerable<Crumb<T>> Breadcrumbs { get; }
Both have the same generic type parameter T, so the question is whether BinaryTreeZipper<T> may form a functor? We now know that the answer is affirmative if BinaryTree<T> and IEnumerable<Crumb<T>> are both functors.
For now, believe me when I claim that this is the case. This means that you can add a Select method to the class:
public BinaryTreeZipper<TResult> Select<TResult>(Func<T, TResult> selector) { return new BinaryTreeZipper<TResult>( Tree.Select(selector), Breadcrumbs.Select(c => c.Select(selector))); }
By now, this should hardly be surprising: Call Select on each constituent functor and create a proper return value from the results.
Higher arities #
All examples have involved products of only two functors, but the result generalizes to higher arities. To gain an understanding of why, consider that it's always possible to rewrite tuples of higher arities as nested pairs. As an example, a triple like (42, "foo", True) can be rewritten as (42, ("foo", True)) without loss of information. The latter representation is a pair (a two-tuple) where the first element is 42, but the second element is another pair. These two representations are isomorphic, meaning that we can go back and forth without losing data.
By induction you can generalize this result to any arity. The point is that the only data type you need to describe a product is a pair.
Haskell's base library defines a specialized container called Product for this very purpose: If you have two Functor instances, you can Pair them up, and they become a single Functor.
Let's start with a Pair of Maybe and a list:
ghci> Pair (Just "foo") ["bar", "baz", "qux"] Pair (Just "foo") ["bar","baz","qux"]
This is a single 'object', if you will, that composes those two Functor instances. This means that you can map over it:
ghci> elem 'b' <$> Pair (Just "foo") ["bar", "baz", "qux"] Pair (Just False) [True,True,False]
Here I've used the infix <$> operator as an alternative to fmap. By composing with elem 'b', I'm asking every value inside the container whether or not it contains the character b. The Maybe value doesn't, while the first two list elements do.
If you want to compose three, rather than two, Functor instances, you just nest the Pairs, just like you can nest tuples:
ghci> elem 'b' <$> Pair (Identity "quux") (Pair (Just "foo") ["bar", "baz", "qux"]) Pair (Identity False) (Pair (Just False) [True,True,False])
This example now introduces the Identity container as a third Functor instance. I could have used any other Functor instance instead of Identity, but some of them are more awkward to create or display. For example, the Reader or State functors have no Show instances in Haskell, meaning that GHCi doesn't know how to print them as values. Other Functor instances didn't work as well for the example, since they tend to be more awkward to create. As an example, any non-trivial Tree requires substantial editor space to express.
Conclusion #
A product of functors may itself be made a functor. The examples shown in this article are all constrained to two functors, but if you have a product of three, four, or more functors, that product still gives rise to a functor.
This is useful to know, particularly if you're working in a language with only partial support for functors. Mainstream languages aren't going to automatically turn such products into functors, in the way that Haskell's Product container almost does. Thus, knowing when you can safely give your generic types a Select method or map function may come in handy.
There are more rules like this one. The next article examines another.
Next: Functor sums.
A Binary Tree Zipper in C#
A port of another Haskell example, still just because.
This article is part of a series about Zippers. In this one, I port the Zipper data structure from the Learn You a Haskell for Great Good! article also called Zippers.
A word of warning: I'm assuming that you're familiar with the contents of that article, so I'll skip the pedagogical explanations; I can hardly do it better that it's done there. Additionally, I'll make heavy use of certain standard constructs to port Haskell code, most notably Church encoding to model sum types in languages that don't natively have them. Such as C#. In some cases, I'll implement the Church encoding using the data structure's catamorphism. Since the cyclomatic complexity of the resulting code is quite low, you may be able to follow what's going on even if you don't know what Church encoding or catamorphisms are, but if you want to understand the background and motivation for that style of programming, you can consult the cited resources.
The code shown in this article is available on GitHub.
Binary tree initialization and structure #
In the Haskell code, the binary Tree type is a recursive sum type, defined on a single line of code. C#, on the other hand, has no built-in language construct that supports sum types, so a more elaborate solution is required. At least two options are available to us. One is to model a sum type as a Visitor. Another is to use Church encoding. In this article, I'll do the latter.
I find the type name (Tree) used in the Zippers article a bit too vague, and since I consider explicit better than implicit, I'll use a more precise class name:
public sealed class BinaryTree<T>
Even so, there are different kinds of binary trees. In a previous article I've shown a catamorphism for a full binary tree. This variation is not as strict, since it allows a node to have zero, one, or two children. Or, strictly speaking, a node always has exactly two children, but both, or one of them, may be empty. BinaryTree<T> uses Church encoding to distinguish between the two, but we'll return to that in a moment.
First, we'll examine how the class allows initialization:
private readonly IBinaryTree root; private BinaryTree(IBinaryTree root) { this.root = root; } public BinaryTree() : this(Empty.Instance) { } public BinaryTree(T value, BinaryTree<T> left, BinaryTree<T> right) : this(new Node(value, left.root, right.root)) { }
The class uses a private root object to implement behaviour, and constructor chaining for initialization. The master constructor is private, since the IBinaryTree interface is private. The parameterless constructor implicitly indicates an empty node, whereas the other public constructor indicates a node with a value and two children. Yes, I know that I just wrote that explicit is better than implicit, but it turns out that with the target-typed new operator feature in C#, constructing trees in code becomes easier with this design choice:
BinaryTree<int> sut = new( 42, new(), new(2, new(), new()));
As the variable name suggests, I've taken this code example from a unit test.
Private interface #
The class delegates method calls to the root field, which is an instance of the private, nested IBinaryTree interface:
private interface IBinaryTree { TResult Aggregate<TResult>( Func<TResult> whenEmpty, Func<T, TResult, TResult, TResult> whenNode); }
Why is IBinaryTree a private interface? Why does that interface even exist?
To be frank, I could have chosen another implementation strategy. Since there's only two mutually exclusive alternatives (node or empty), I could also have indicated which is which with a Boolean flag. You can see an example of that implementation tactic in the Table class in the sample code that accompanies Code That Fits in Your Head.
Using a Boolean flag, however, only works when there are exactly two choices. If you have three or more, things because more complicated. You could try to use an enum, but in most languages, these tend to be nothing but glorified integers, and are typically not type-safe. If you define a three-way enum, there's no guarantee that a value of that type takes only one of these three values, and a good compiler will typically insist that you check for any other value as well. The C# compiler certainly does.
Church encoding offers a better alternative, but since it makes use of polymorphism, the most idiomatic choice in C# is either an interface or a base class. Since I favour interfaces over base classes, that's what I've chosen here, but for the purposes of this little digression, it makes no difference: The following argument applies to base classes as well.
An interface (or base class) suggests to users of an API that they can implement it in order to extend behaviour. That's an impression I don't wish to give client developers. The purpose of the interface is exclusively to enable double dispatch to work. There's only two implementations of the IBinaryTree interface, and under no circumstances should there be more.
The interface is an implementation detail, which is why both it, and its implementations, are private.
Binary tree catamorphism #
The IBinaryTree interface defines a catamorphism for the BinaryTree<T> class. Since we may often view a catamorphism as a sort of 'generalized fold', and since these kinds of operations in C# are typically called Aggregate, that's what I've called the method.
An aggregate function affords a way to traverse a data structure and collect information into a single value, here of type TResult. The return type may, however, be a complex type, including another BinaryTree<T>. You'll see examples of complex return values later in this article.
As already discussed, there are exactly two implementations of IBinaryTree. The one representing an empty node is the simplest:
private sealed class Empty : IBinaryTree { public readonly static Empty Instance = new(); private Empty() { } public TResult Aggregate<TResult>( Func<TResult> whenEmpty, Func<T, TResult, TResult, TResult> whenNode) { return whenEmpty(); } }
The Aggregate implementation unconditionally calls the supplied whenEmpty function, which returns some TResult value unknown to the Empty class.
Although not strictly necessary, I've made the class a Singleton. Since I like to take advantage of structural equality to write better tests, it was either that, or overriding Equals and GetHashCode.
The other implementation gets around that problem by being a record:
private sealed record Node(T Value, IBinaryTree Left, IBinaryTree Right) : IBinaryTree { public TResult Aggregate<TResult>( Func<TResult> whenEmpty, Func<T, TResult, TResult, TResult> whenNode) { return whenNode( Value, Left.Aggregate(whenEmpty, whenNode), Right.Aggregate(whenEmpty, whenNode)); } }
It, too, unconditionally calls one of the two functions passed to its Aggregate method, but this time whenNode. It does that, however, by first recursively calling Aggregate on both Left and Right. It needs to do that because the whenNode function expects the subtrees to have been already converted to values of the TResult return type. This is a common pattern with catamorphisms, and takes a bit of time getting used to. You can see similar examples in the articles Tree catamorphism, Rose tree catamorphism, and Full binary tree catamorphism.
The BinaryTree<T> class defines a public Aggregate method that delegates to its root field:
public TResult Aggregate<TResult>( Func<TResult> whenEmpty, Func<T, TResult, TResult, TResult> whenNode) { return root.Aggregate(whenEmpty, whenNode); }
The astute reader may now remark that the Aggregate method doesn't look like a Church encoding.
Binary tree Church encoding #
A Church encoding will typically have a Match method that enables client code to match on all the alternative cases in the sum type, without those confusing already-converted TResult values. It turns out that you can implement the desired Match method with the Aggregate method.
One of the advantages of doing meaningless coding exercises like this one is that you can pursue various ideas that interest you. One idea that interests me is the potential universality of catamorphisms. I conjecture that a catamorphism is an algebraic data type's universal API, and that you can implement all other methods or functions with it. I admit that I haven't done much research in the form of perusing existing literature, but at least it seems to be the case conspicuously often.
As it is here.
public TResult Match<TResult>( Func<TResult> whenEmpty, Func<T, BinaryTree<T>, BinaryTree<T>, TResult> whenNode) { return root .Aggregate( () => (tree: new BinaryTree<T>(), result: whenEmpty()), (x, l, r) => ( new BinaryTree<T>(x, l.tree, r.tree), whenNode(x, l.tree, r.tree))) .result; }
Now, I readily admit that it took me a couple of hours tossing and turning in my bed before this solution came to me. I don't find it intuitive at all, but it works.
The Aggregate method requires that the whenNode function's left and right values are of the same TResult type as the return type. How do we consolidate that requirement with the Match method's variation, where its whenNode function requires the left and right values to be BinaryTree<T> values, but the return type still TResult?
The way out of this conundrum, it turns out, is to combine both in a tuple. Thus, when Match calls Aggregate, the implied TResult type is not the TResult visible in the Match method declaration. Rather, it's inferred to be of the type (BinaryTree<T>, TResult). That is, a tuple where the first element is a BinaryTree<T> value, and the second element is a TResult value. The C# compiler's type inference engine then figures out that (BinaryTree<T>, TResult) must also be the return type of the Aggregate method call.
That's not what Match should return, but the second tuple element contains a value of the correct type, so it returns that. Since I've given the tuple elements names, the Match implementation accomplishes that by returning the result tuple field.
Breadcrumbs #
That's just the tree that we want to zip. So far, we can only move from root to branches, but not the other way. Before we can define a Zipper for the tree, we need a data structure to store breadcrumbs (the navigation log, if you will).
In Haskell it's just another one-liner, but in C# this requires another full-fledged class:
public sealed class Crumb<T>
It's another sum type, so once more, I make the constructor private and use a private class field for the implementation:
private readonly ICrumb imp; private Crumb(ICrumb imp) { this.imp = imp; } internal static Crumb<T> Left(T value, BinaryTree<T> right) { return new(new LeftCrumb(value, right)); } internal static Crumb<T> Right(T value, BinaryTree<T> left) { return new(new RightCrumb(value, left)); }
To stay consistent throughout the code base, I also use Church encoding to distinguish between a Left and Right breadcrumb, and the technique is similar. First, define a private interface:
private interface ICrumb { TResult Match<TResult>( Func<T, BinaryTree<T>, TResult> whenLeft, Func<T, BinaryTree<T>, TResult> whenRight); }
Then, use private nested types to implement the interface.
private sealed record LeftCrumb(T Value, BinaryTree<T> Right) : ICrumb { public TResult Match<TResult>( Func<T, BinaryTree<T>, TResult> whenLeft, Func<T, BinaryTree<T>, TResult> whenRight) { return whenLeft(Value, Right); } }
The RightCrumb record is essentially just the 'mirror image' of the LeftCrumb record, and just as was the case with BinaryTree<T>, the Crumb<T> class exposes an externally accessible Match method that just delegates to the private class field:
public TResult Match<TResult>( Func<T, BinaryTree<T>, TResult> whenLeft, Func<T, BinaryTree<T>, TResult> whenRight) { return imp.Match(whenLeft, whenRight); }
Finally, all the building blocks are ready for the actual Zipper.
Zipper data structure and initialization #
In the Haskell code, the Zipper is another one-liner, and really just a type alias. In C#, once more, we're going to need a full class.
public sealed class BinaryTreeZipper<T>
The Haskell article simply calls this type alias Zipper, but I find that name too general, since there's more than one kind of Zipper. I think I understand that the article chooses that name for didactic reasons, but here I've chosen a more consistent disambiguation scheme, so I've named the class BinaryTreeZipper<T>.
The Haskell example is just a type alias for a tuple, and the C# class is similar, although with significantly more ceremony:
public BinaryTree<T> Tree { get; } public IEnumerable<Crumb<T>> Breadcrumbs { get; } private BinaryTreeZipper( BinaryTree<T> tree, IEnumerable<Crumb<T>> breadcrumbs) { Tree = tree; Breadcrumbs = breadcrumbs; } public BinaryTreeZipper(BinaryTree<T> tree) : this(tree, []) { }
I've here chosen to add an extra bit of encapsulation by making the master constructor private. This prevents client code from creating an arbitrary object with breadcrumbs without having navigated through the tree. To be honest, I don't think it violates any contract even if we allow this, but it at least highlights that the Breadcrumbs role is to keep a log of what previously happened to the object.
Navigation #
We can now reproduce the navigation functions from the Haskell article.
public BinaryTreeZipper<T>? GoLeft() { return Tree.Match<BinaryTreeZipper<T>?>( whenEmpty: () => null, whenNode: (x, l, r) => new BinaryTreeZipper<T>( l, Breadcrumbs.Prepend(Crumb.Left(x, r)))); }
Going left 'pattern-matches' on the Tree and, if not empty, constructs a new BinaryTreeZipper object with the left tree, and a Left breadcrumb that stores the 'current' node value and the right subtree. If the 'current' node is empty, on the other hand, the method returns null. This possibility is explicitly indicated by the BinaryTreeZipper<T>? return type; notice the question mark, which indicates that the value may be null. If you're working in a context or language where that feature isn't available, you may instead consider taking advantage of the Maybe monad (which is also what you'd idiomatically do in Haskell).
The GoRight method is similar to GoLeft.
We may also attempt to navigate up in the tree, undoing our last downward move:
public BinaryTreeZipper<T>? GoUp() { if (!Breadcrumbs.Any()) return null; var head = Breadcrumbs.First(); var tail = Breadcrumbs.Skip(1); return head.Match( whenLeft: (x, r) => new BinaryTreeZipper<T>( new BinaryTree<T>(x, Tree, r), tail), whenRight: (x, l) => new BinaryTreeZipper<T>( new BinaryTree<T>(x, l, Tree), tail)); }
This is another operation that may fail. If we're already at the root of the tree, there are no Breadcrumbs, in which case the only option is to return a value indicating that the operation failed; here, null, but in other languages perhaps None or Nothing.
If, on the other hand, there's at least one breadcrumb, the GoUp method uses the most recent one (head) to construct a new BinaryTreeZipper<T> object that reconstitutes the opposite (sibling) subtree and the parent node. It does that by 'pattern-matching' on the head breadcrumb, which enables it to distinguish a left breadcrumb from a right breadcrumb.
Finally, we may keep trying to GoUp until we reach the root:
public BinaryTreeZipper<T> TopMost() { return GoUp()?.TopMost() ?? this; }
You'll see an example of that a little later.
Modifications #
Continuing the port of the Haskell code, we can Modify the current node with a function:
public BinaryTreeZipper<T> Modify(Func<T, T> f) { return new BinaryTreeZipper<T>( Tree.Match( whenEmpty: () => new BinaryTree<T>(), whenNode: (x, l, r) => new BinaryTree<T>(f(x), l, r)), Breadcrumbs); }
This operation always succeeds, since it chooses to ignore the change if the tree is empty. Thus, there's no question mark on the return type, indicating that the method never returns null.
Finally, we may replace a node with a new subtree:
public BinaryTreeZipper<T> Attach(BinaryTree<T> tree) { return new BinaryTreeZipper<T>(tree, Breadcrumbs); }
The following unit test demonstrates a combination of several of the methods shown above:
[Fact] public void AttachAndGoTopMost() { var sut = new BinaryTreeZipper<char>(freeTree); var farLeft = sut.GoLeft()?.GoLeft()?.GoLeft()?.GoLeft(); var actual = farLeft?.Attach(new('Z', new(), new())).TopMost(); Assert.NotNull(actual); Assert.Equal( new('P', new('O', new('L', new('N', new('Z', new(), new()), new()), new('T', new(), new())), new('Y', new('S', new(), new()), new('A', new(), new()))), new('L', new('W', new('C', new(), new()), new('R', new(), new())), new('A', new('A', new(), new()), new('C', new(), new())))), actual.Tree); Assert.Empty(actual.Breadcrumbs); }
The test starts with freeTree (not shown) and first navigates to the leftmost empty node. Here it uses Attach to add a new 'singleton' subtree with the value 'Z'. Finally, it uses TopMost to return to the root node.
In the Assert phase, the test verifies that the actual object contains the expected values.
Conclusion #
The Tree Zipper shown here is a port of the example given in the Haskell Zippers article. As I've already discussed in the introduction article, this data structure doesn't make much sense in C#, where you can easily implement a navigable tree with two-way links. Even if this requires state mutation, you can package such a data structure in a proper object with good encapsulation, so that operations don't leave any dangling pointers or the like.
As far as I can tell, the code shown in this article isn't useful in production code, but I hope that, at least, you still learned something from it. I always learn a new thing or two from doing programming exercises and writing about them, and this was no exception.
In the next article, I continue with the final of the Haskell article's three examples.
Next: FSZipper in C#.
Keeping cross-cutting concerns out of application code
Don't inject third-party dependencies. Use Decorators.
I recently came across a Stack Overflow question that reminded me of a topic I've been meaning to write about for a long time: Cross-cutting concerns.
When it comes to the usual suspects, logging, fault tolerance, caching, the best solution is usually to apply the Decorator pattern.
I often see code that uses Dependency Injection (DI) to inject, say, a logging interface into application code. You can see an example of that in Repeatable execution, as well as a suggestion for a better design. Not surprisingly, the better design involves logging Decorators.
The Stack Overflow question isn't about logging, but rather about fault tolerance; Circuit Breaker, retry policies, timeouts, etc.
Injected concern #
The question does a good job of presenting a minimal, reproducible example. At the outset, the code looks like this:
public class MyApi { private readonly ResiliencePipeline pipeline; private readonly IOrganizationService service; public MyApi(ResiliencePipelineProvider<string> provider, IOrganizationService service) { this.pipeline = provider.GetPipeline("retry-pipeline"); this.service = service; } public List<string> GetSomething(QueryByAttribute query) { var result = this.pipeline.Execute(() => service.RetrieveMultiple(query)); return result.Entities.Cast<string>().ToList(); } }
The Stack Overflow question asks how to test this implementation, but I'd rather take the example as an opportunity to discuss design alternatives. Not surprisingly, it turns out that with a more decoupled design, testing becomes easier, too.
Before we proceed, a few words about this example code. I assume that this isn't Andy Cooke's actual production code. Rather, I interpret it as a reduced example that highlights the actual question. This is important because you might ask: Why bother testing two lines of code?
Indeed, as presented, the GetSomething method is so simple that you may consider not testing it. Thus, I interpret the second line of code as a stand-in for more complicated production code. Hold on to that thought, because once I'm done, that's all that's going to be left, and you may then think that it's so simple that it really doesn't warrant all this hoo-ha.
Coupling #
As shown, the MyApi class is coupled to Polly, because ResiliencePipeline is defined by that library. To be clear, all I've heard is that Polly is a fine library. I've used it for a few projects myself, but I also admit that I haven't that much experience with it. I'd probably use it again the next time I need a Circuit Breaker or similar, so the following discussion isn't a denouncement of Polly. Rather, it applies to all third-party dependencies, or perhaps even dependencies that are part of your language's base library.
Coupling is a major cause of spaghetti code and code rot in general. To write sustainable code, you should be cognizant of coupling. The most decoupled code is code that you can easily delete.
This doesn't mean that you shouldn't use high-quality third-party libraries like Polly. Among myriads of software engineering heuristics, we know that we should be aware of the not-invented-here syndrome.
When it comes to classic cross-cutting concerns, the Decorator pattern is usually a better design than injecting the concern into application code. The above example clearly looks innocuous, but imagine injecting both a ResiliencePipeline, a logger, and perhaps a caching service, and your real application code eventually disappears in 'infrastructure code'.
It's not that we don't want to have these third-party dependencies, but rather that we want to move them somewhere else.
Resilient Decorator #
The concern in the above example is the desire to make the IOrganizationService dependency more resilient. The MyApi class only becomes more resilient as a transitive effect. The first refactoring step, then, is to introduce a resilient Decorator.
public sealed class ResilientOrganizationService( ResiliencePipeline pipeline, IOrganizationService inner) : IOrganizationService { public QueryResult RetrieveMultiple(QueryByAttribute query) { return pipeline.Execute(() => inner.RetrieveMultiple(query)); } }
As Decorators must, this class composes another IOrganizationService while also implementing that interface itself. It does so by being an Adapter over the Polly API.
I've applied Nikola Malovic's 4th law of DI:
"Every constructor of a class being resolved should not have any implementation other then accepting a set of its own dependencies."
Instead of injecting a ResiliencePipelineProvider<string> only to call GetPipeline on it, it just receives a ResiliencePipeline and saves the object for use in the RetrieveMultiple method. It does that via a primary constructor, which is a recent C# language addition. It's just syntactic sugar for Constructor Injection, and as usual F# developers should feel right at home.
Simplifying MyApi #
Now that you have a resilient version of IOrganizationService you don't need to have any Polly code in MyApi. Remove it and simplify:
public class MyApi { private readonly IOrganizationService service; public MyApi(IOrganizationService service) { this.service = service; } public List<string> GetSomething(QueryByAttribute query) { var result = service.RetrieveMultiple(query); return result.Entities.Cast<string>().ToList(); } }
As promised, there's almost nothing left of it now, but I'll remind you that I consider the second line of GetSomething as a stand-in for something more complicated that you might need to test. As it is now, though, testing it is trivial:
[Theory] [InlineData("foo", "bar", "baz")] [InlineData("qux", "quux", "corge")] [InlineData("grault", "garply", "waldo")] public void GetSomething(params string[] expected) { var service = new Mock<IOrganizationService>(); service .Setup(s => s.RetrieveMultiple(new QueryByAttribute())) .Returns(new QueryResult(expected)); var sut = new MyApi(service.Object); var actual = sut.GetSomething(new QueryByAttribute()); Assert.Equal(expected, actual); }
The larger point, however, is that not only have you now managed to keep third-party dependencies out of your application code, you've also simplified it and made it easier to test.
Composition #
You can still create a resilient MyApi object in your Composition Root:
var service = new ResilientOrganizationService(pipeline, inner); var myApi = new MyApi(service);
Decomposing the problem in this way, you decouple your application code from third-party dependencies. You can define ResilientOrganizationService in the application's Composition Root, which also keeps the Polly dependency there. Even so, you can implement MyApi as part of your application layer.
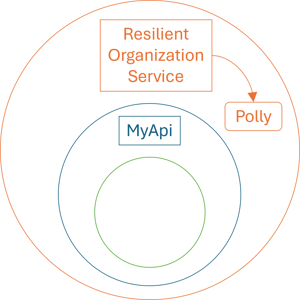
I usually illustrate Ports and Adapters, or, if you will, Clean Architecture as concentric circles, but in this diagram I've skewed the circles to make space for the boxes. In other words, the diagram is 'not to scale'. Ideally, the outermost layer is much smaller and thinner than any of the the other layers. I've also included an inner green layer which indicates the architecture's Domain Model, but since I assume that MyApi is part of some application layer, I've left the Domain Model empty.
Reasons to decouple #
Why is it important to decouple application code from Polly? First, keep in mind that in this discussion Polly is just a stand-in for any third-party dependency. It's up to you as a software architect to decide how you'll structure your code, but third-party dependencies are one of the first things I look for. A third-party component changes with time, and often independently of your base platform. You may have to deal with breaking changes or security patches at inopportune times. The organization that maintains the component may cease to operate. This happens to commercial entities and open-source contributors alike, although for different reasons.
Second, even a top-tier library like Polly will undergo changes. If your time horizon is five to ten years, you'll be surprised how much things change. You may protest that no-one designs software systems with such a long view, but I think that if you ask the business people involved with your software, they most certainly expect your system to last a long time.
I believe that I heard on a podcast that some Microsoft teams had taken a dependency on Polly. Assuming, for the sake of argument, that this is true, while we may not wish to depend on some random open-source component, depending on Polly is safe, right? In the long run, it isn't. Five years ago, you had the same situation with Json.NET, but then Microsoft hired James Newton-King and had him make a JSON API as part of the .NET base library. While Json.NET isn't dead by any means, now you have two competing JSON libraries, and Microsoft uses their own in the frameworks and libraries that they release.
Deciding to decouple your application code from a third-party component is ultimately a question of risk management. It's up to you to make the bet. Do you pay the up-front cost of decoupling, or do you postpone it, hoping it'll never be necessary?
I usually do the former, because the cost is low, and there are other benefits as well. As I've already touched on, unit testing becomes easier.
Configuration #
Since Polly only lives in the Composition Root, you'll also need to define the ResiliencePipeline there. You can write the code that creates that pieline wherever you like, but it might be natural to make it a creation function on the ResilientOrganizationService class:
public static ResiliencePipeline CreatePipeline() { return new ResiliencePipelineBuilder() .AddRetry(new RetryStrategyOptions { MaxRetryAttempts = 4 }) .AddTimeout(TimeSpan.FromSeconds(1)) .Build(); }
That's just an example, and perhaps not what you'd like to do. Perhaps you rather want some of these values to be defined in a configuration file. Thus, this isn't what you have to do, but rather what you could do.
If you use this option, however, you could take the return value of this method and inject it into the ResilientOrganizationService constructor.
Conclusion #
Cross-cutting concerns, like caching, logging, security, or, in this case, fault tolerance, are usually best addressed with the Decorator pattern. In this article, you saw an example of using the Decorator pattern to decouple the concern of fault tolerance from the consumer of the service that you need to handle in a fault-tolerant manner.
The specific example dealt with the Polly library, but the point isn't that Polly is a particularly nasty third-party component that you need to protect yourself against. Rather, it just so happened that I came across a Stack Overflow question that used Polly, and I though it was a a nice example.
As far as I can tell, Polly is actually one of the top .NET open-source packages, so this article is not a denouncement of Polly. It's just a sketch of how to move useful dependencies around in your code base to make sure that they impact your application code as little as possible.
A List Zipper in C#
A port of a Haskell example, just because.
This article is part of a series about Zippers. In this one, I port the ListZipper data structure from the Learn You a Haskell for Great Good! article also called Zippers.
A word of warning: I'm assuming that you're familiar with the contents of that article, so I'll skip the pedagogical explanations; I can hardly do it better that it's done there.
The code shown in this article is available on GitHub.
Initialization and structure #
In the Haskell code, ListZipper is just a type alias, but C# doesn't have that, so instead, we'll have to introduce a class.
public sealed class ListZipper<T> : IEnumerable<T>
Since it implements IEnumerable<T>, it may be used like any other sequence, but it also comes with some special operations that enable client code to move forward and backward, as well as inserting and removing values.
The class has the following fields, properties, and constructors:
private readonly IEnumerable<T> values; public IEnumerable<T> Breadcrumbs { get; } private ListZipper(IEnumerable<T> values, IEnumerable<T> breadcrumbs) { this.values = values; Breadcrumbs = breadcrumbs; } public ListZipper(IEnumerable<T> values) : this(values, []) { } public ListZipper(params T[] values) : this(values.AsEnumerable()) { }
It uses constructor chaining to initialize a ListZipper object with proper encapsulation. Notice that the master constructor is private. This prevents client code from initializing an object with arbitrary Breadcrumbs. Rather, the Breadcrumbs (the log, if you will) is going to be the result of various operations performed by client code, and only the ListZipper class itself can use this constructor.
You may consider the constructor that takes a single IEnumerable<T> as the 'main' public constructor, and the other one as a convenience that enables a client developer to write code like new ListZipper<string>("foo", "bar", "baz").
The class' IEnumerable<T> implementation only enumerates the values:
public IEnumerator<T> GetEnumerator() { return values.GetEnumerator(); }
In other words, when enumerating a ListZipper, you only get the 'forward' values. Client code may still examine the Breadcrumbs, since this is a public property, but it should have little need for that.
(I admit that making Breadcrumbs public is a concession to testability, since it enabled me to write assertions against this property. It's a form of structural inspection, which is a technique that I use much less than I did a decade ago. Still, in this case, while you may argue that it violates information hiding, it at least doesn't allow client code to put an object in an invalid state. Had the ListZipper class been a part of a reusable library, I would probably have hidden that data, too, but since this is exercise code, I found this an acceptable compromise. Notice, too, that in the original Haskell code, the breadcrumbs are available to client code.)
Regular readers of this blog may be aware that I usually favour IReadOnlyCollection<T> over IEnumerable<T>. Here, on the other hand, I've allowed values to be any IEnumerable<T>, which includes infinite sequences. I decided to do that because Haskell lists, too, may be infinite, and as far as I can tell, ListZipper actually does work with infinite sequences. I have, at least, written a few tests with infinite sequences, and they pass. (I may still have missed an edge case or two. I can't rule that out.)
Movement #
It's not much fun just being able to initialize an object. You also want to be able to do something with it, such as moving forward:
public ListZipper<T>? GoForward() { var head = values.Take(1); if (!head.Any()) return null; var tail = values.Skip(1); return new ListZipper<T>(tail, head.Concat(Breadcrumbs)); }
You can move forward through any IEnumerable, so why make things so complicated? The benefit of this GoForward method (function, really) is that it records where it came from, which means that moving backwards becomes an option:
public ListZipper<T>? GoBack() { var head = Breadcrumbs.Take(1); if (!head.Any()) return null; var tail = Breadcrumbs.Skip(1); return new ListZipper<T>(head.Concat(values), tail); }
This test may serve as an example of client code that makes use of those two operations:
[Fact] public void GoBack1() { var sut = new ListZipper<int>(1, 2, 3, 4); var actual = sut.GoForward()?.GoForward()?.GoForward()?.GoBack(); Assert.Equal([3, 4], actual); Assert.Equal([2, 1], actual?.Breadcrumbs); }
Going forward takes the first element off values and adds it to the front of Breadcrumbs. Going backwards is nearly symmetrical: It takes the first element off the Breadcrumbs and adds it back to the front of the values. Used in this way, Breadcrumbs works as a stack.
Notice that both GoForward and GoBack admit the possibility of failure. If values is empty, you can't go forward. If Breadcrumbs is empty, you can't go back. In both cases, the functions return null, which are also indicated by the ListZipper<T>? return types; notice the question mark, which indicates that the value may be null. If you're working in a context or language where that feature isn't available, you may instead consider taking advantage of the Maybe monad (which is also what you'd idiomatically do in Haskell).
To be clear, the Zippers article does discuss handling failures using Maybe, but only applies it to its binary tree example. Thus, the error handling shown here is my own addition.
Modifications #
In addition to moving back and forth in the list, we can also modify it. The following operations are also not in the Zippers article, but are rather my own contributions. Adding a new element is easy:
public ListZipper<T> Insert(T value) { return new ListZipper<T>(values.Prepend(value), Breadcrumbs); }
Notice that this operation is always possible. Even if the list is empty, we can Insert a value. In that case, it just becomes the list's first and only element.
A simple test demonstrates usage:
[Fact] public void InsertAtFocus() { var sut = new ListZipper<string>("foo", "bar"); var actual = sut.GoForward()?.Insert("ploeh").GoBack(); Assert.NotNull(actual); Assert.Equal(["foo", "ploeh", "bar"], actual); Assert.Empty(actual.Breadcrumbs); }
Likewise, we may attempt to remove an element from the list:
public ListZipper<T>? Remove() { if (!values.Any()) return null; return new ListZipper<T>(values.Skip(1), Breadcrumbs); }
Contrary to Insert, the Remove operation will fail if values is empty. Notice that this doesn't necessarily imply that the list as such is empty, but only that the focus is at the end of the list (which, of course, never happens if values is infinite):
[Fact] public void RemoveAtEnd() { var sut = new ListZipper<string>("foo", "bar").GoForward()?.GoForward(); var actual = sut?.Remove(); Assert.Null(actual); Assert.NotNull(sut); Assert.Empty(sut); Assert.Equal(["bar", "foo"], sut.Breadcrumbs); }
In this example, the focus is at the end of the list, so there's nothing to remove. The list, however, is not empty, but all the data currently reside in the Breadcrumbs.
Finally, we can combine insertion and removal to implement a replacement operation:
public ListZipper<T>? Replace(T newValue) { return Remove()?.Insert(newValue); }
As the name implies, this operation replaces the value currently in focus with a completely different value. Here's an example:
[Fact] public void ReplaceAtFocus() { var sut = new ListZipper<string>("foo", "bar", "baz"); var actual = sut.GoForward()?.Replace("qux")?.GoBack(); Assert.NotNull(actual); Assert.Equal(["foo", "qux", "baz"], actual); Assert.Empty(actual.Breadcrumbs); }
Once more, this may fail if the current focus is empty, so Replace also returns a nullable value.
Conclusion #
For a C# developer, the ListZipper<T> class looks odd. Why would you ever want to use this data structure? Why not just use List<T>?
As I hope I've made clear in the introduction article, I can't, indeed, think of a good reason.
I've gone through this exercise to hone my skills, and to prepare myself for the more intimidating exercise it is to implement a binary tree Zipper.
Next: A Binary Tree Zipper in C#.
Zippers
Some functional programming examples ported to C#, just because.
Many algorithms rely on data structures that enable the implementation to move in more than one way. A simple example is a doubly-linked list, where an algorithm can move both forward and backward from a given element. Other examples are various tree-based algorithms, such as red-black trees where certain operations trigger reorganization of the tree. Yet other data structures, such as Fibonacci heaps, combine doubly-linked lists with trees that allow navigation in more than one direction.
In an imperative programming language, you can easily implement such data structures, as long as the language allows data mutation. Here's a simple example:
var node1 = new Node<string>("foo"); var node2 = new Node<string>("bar") { Previous = node1 }; node1.Next = node2;
It's possible to double-link node1 to node2 by first creating node1. At that point, node2 still doesn't exist, so you can't yet assign node1.Next, but once you've initialized node2, you can mutate the state of node1 by changing its Next property.
When data structures are immutable (as they must be in functional programming) this is no longer possible. How may you get around that limitation?
Alternatives #
Some languages get around this problem in various ways. Haskell, because of its lazy evaluation, enables a technique called tying the knot that, frankly, makes my head hurt.
Even though I write a decent amount of Haskell code, that's not something that I make use of. Usually, it turns out, you can solve most problems by thinking about them differently. By choosing another perspective, and another data structure, you can often arrive at a good, functional solution to your problem.
One family of general-purpose data structures are called Zippers. The general idea is that the data structure has a natural 'focus' (e.g. the head of a list), but it also keeps a record of 'breadcrumbs', that is, where the caller has previously been. This enables client code to 'go back' or 'go up', if the natural direction is to 'go forward' or 'go down'. It's a bit like Event Sourcing, in that every operation leaves a log entry that can later be used to reconstruct what happened. Repeatable Execution also comes to mind, although it's not quite the same.
For an introduction to Zippers, I recommend the excellent and highly readable article Zippers. In this article series, I'm going to assume that you're familiar with the contents of that article.
C# ports #
While I may add more articles to this series in the future, as I'm writing this, I have nothing more planned than writing about how it's possible to implement the article's three Zippers in C#.
Why would you want to do this?
To be honest, for production code, I can't think of a good reason. I did it for a few reasons, most of them didactic. Additionally, writing code for exercise helps you improve. If you know enough Haskell to understand what's going on in the Zippers article, you may consider porting some of it to your favourite language, as an exercise.
It may help you grokking functional programming.
That's really it, though. There's no reason to use Zippers in a language like C#, which idiomatically makes use of mutation. If you want a doubly-linked list, you can just write code as shown in the beginning of this article.
If you're interested in an F# perspective on Zippers, Tomas Petricek has a cool article: Processing trees with F# zipper computation.
Conclusion #
Zippers constitute a family of data structures that enables you to move in multiple directions. Left and right in a list. Up or down in a tree. For an imperative programmer, that's literally just another day at the office, but in disciplined functional programming, making cyclic graphs can be surprisingly tricky.
Even in functional programming, I rarely reach for a Zipper, since I can often find a library with a higher level of abstraction that does what I need it to do. Still, learning of new ways to solve problems never seems a waste to me.
In the next three articles, I'll go through the examples from the Zipper article and show how I ported them to C#. While that article starts with a binary tree, I'll instead begin with the doubly-linked list, since it's the simplest of the three.
Next: A List Zipper in C#.
Using only a Domain Model to persist restaurant table configurations
A data architecture example in C# and ASP.NET.
This is part of a small article series on data architectures. In this, the third instalment, you'll see an alternative way of modelling data in a server-based application. One that doesn't rely on statically typed classes to model data. As the introductory article explains, the example code shows how to create a new restaurant table configuration, or how to display an existing resource. The sample code base is an ASP.NET 8.0 REST API.
Keep in mind that while the sample code does store data in a relational database, the term table in this article mainly refers to physical tables, rather than database tables.
The idea is to use 'raw' serialization APIs to handle communication with external systems. For the presentation layer, the example even moves representation concerns to middleware, so that it's nicely abstracted away from the application layer.
An architecture diagram like this attempts to capture the design:
Here, the arrows indicate mappings, not dependencies.
Like in the DTO-based Ports and Adapters architecture, the goal is to being able to design Domain Models unconstrained by serialization concerns, but also being able to format external data unconstrained by Reflection-based serializers. Thus, while this architecture is centred on a Domain Model, there are no Data Transfer Objects (DTOs) to represent JSON, XML, or database rows.
HTTP interaction #
To establish the context of the application, here's how HTTP interactions may play out. The following is a copy of the identically named section in the article Using Ports and Adapters to persist restaurant table configurations, repeated here for your convenience.
A client can create a new table with a POST HTTP request:
POST /tables HTTP/1.1
content-type: application/json
{ "communalTable": { "capacity": 16 } }
Which might elicit a response like this:
HTTP/1.1 201 Created Location: https://example.com/Tables/844581613e164813aa17243ff8b847af
Clients can later use the address indicated by the Location header to retrieve a representation of the resource:
GET /Tables/844581613e164813aa17243ff8b847af HTTP/1.1 accept: application/json
Which would result in this response:
HTTP/1.1 200 OK
Content-Type: application/json; charset=utf-8
{"communalTable":{"capacity":16}}
By default, ASP.NET handles and returns JSON. Later in this article you'll see how well it deals with other data formats.
Boundary #
ASP.NET supports some variation of the model-view-controller (MVC) pattern, and Controllers handle HTTP requests. At the outset, the action method that handles the POST request looks like this:
[HttpPost] public async Task<IActionResult> Post(Table table) { var id = Guid.NewGuid(); await repository.Create(id, table).ConfigureAwait(false); return new CreatedAtActionResult( nameof(Get), null, new { id = id.ToString("N") }, null); }
While this looks identical to the Post method for the Shared Data Model architecture, it's not, because it's not the same Table class. Not by a long shot. The Table class in use here is the one originally introduced in the article Serializing restaurant tables in C#, with a few inconsequential differences.
How does a Controller action method receive an input parameter directly in the form of a Domain Model, keeping in mind that this particular Domain Model is far from serialization-friendly? The short answer is middleware, which we'll get to in a moment. Before we look at that, however, let's also look at the Get method that supports HTTP GET requests:
[HttpGet("{id}")] public async Task<IActionResult> Get(string id) { if (!Guid.TryParseExact(id, "N", out var guid)) return new BadRequestResult(); Table? table = await repository.Read(guid).ConfigureAwait(false); if (table is null) return new NotFoundResult(); return new OkObjectResult(table); }
This, too, looks exactly like the Shared Data Model architecture, again with the crucial difference that the Table class is completely different. The Get method just takes the table object and wraps it in an OkObjectResult and returns it.
The Table class is, in reality, extraordinarily opaque, and not at all friendly to serialization, so how do the service turn it into JSON?
JSON middleware #
Most web frameworks come with extensibility points where you can add middleware. A common need is to be able to add custom serializers. In ASP.NET they're called formatters, and can be added at application startup:
builder.Services.AddControllers(opts => { opts.InputFormatters.Insert(0, new TableJsonInputFormatter()); opts.OutputFormatters.Insert(0, new TableJsonOutputFormatter()); });
As the names imply, TableJsonInputFormatter deserializes JSON input, while TableJsonOutputFormatter serializes strongly typed objects to JSON.
We'll look at each in turn, starting with TableJsonInputFormatter, which is responsible for deserializing JSON documents into Table objects, as used by, for example, the Post method.
JSON input formatter #
You create an input formatter by implementing the IInputFormatter interface, although in this example code base, inheriting from TextInputFormatter is enough:
internal sealed class TableJsonInputFormatter : TextInputFormatter
You can use the constructor to define which media types and encodings the formatter will support:
public TableJsonInputFormatter() { SupportedMediaTypes.Add(MediaTypeHeaderValue.Parse("application/json")); SupportedEncodings.Add(Encoding.UTF8); SupportedEncodings.Add(Encoding.Unicode); }
You'll also need to tell the formatter, which .NET type it supports:
protected override bool CanReadType(Type type) { return type == typeof(Table); }
As far as I can tell, the ASP.NET framework will first determine which action method (that is, which Controller, and which method on that Controller) should handle a given HTTP request. For a POST request, as shown above, it'll determine that the appropriate action method is the Post method.
Since the Post method takes a Table object as input, the framework then goes through the registered formatters and asks them whether they can read from an HTTP request into that type. In this case, the TableJsonInputFormatter answers true only if the type is Table.
When CanReadType answers true, the framework then invokes a method to turn the HTTP request into an object:
public override async Task<InputFormatterResult> ReadRequestBodyAsync( InputFormatterContext context, Encoding encoding) { using var rdr = new StreamReader(context.HttpContext.Request.Body, encoding); var json = await rdr.ReadToEndAsync().ConfigureAwait(false); var table = TableJson.Deserialize(json); if (table is { }) return await InputFormatterResult.SuccessAsync(table).ConfigureAwait(false); else return await InputFormatterResult.FailureAsync().ConfigureAwait(false); }
The ReadRequestBodyAsync method reads the HTTP request body into a string value called json, and then passes the value to TableJson.Deserialize. You can see the implementation of the Deserialize method in the article Serializing restaurant tables in C#. In short, it uses the default .NET JSON parser to probe a document object model. If it can turn the JSON document into a Table value, it does that. Otherwise, it returns null.
The above ReadRequestBodyAsync method then checks if the return value from TableJson.Deserialize is null. If it's not, it wraps the result in a value that indicates success. If it's null, it uses FailureAsync to indicate a deserialization failure.
With this input formatter in place as middleware, any action method that takes a Table parameter will automatically receive a deserialized JSON object, if possible.
JSON output formatter #
The TableJsonOutputFormatter class works much in the same way, but instead derives from the TextOutputFormatter base class:
internal sealed class TableJsonOutputFormatter : TextOutputFormatter
The constructor looks just like the TableJsonInputFormatter, and instead of a CanReadType method, it has a CanWriteType method that also looks identical.
The WriteResponseBodyAsync serializes a Table object to JSON:
public override Task WriteResponseBodyAsync( OutputFormatterWriteContext context, Encoding selectedEncoding) { if (context.Object is Table table) return context.HttpContext.Response.WriteAsync(table.Serialize(), selectedEncoding); throw new InvalidOperationException("Expected a Table object."); }
If context.Object is, in fact, a Table object, the method calls table.Serialize(), which you can also see in the article Serializing restaurant tables in C#. In short, it pattern-matches on the two possible kinds of tables and builds an appropriate abstract syntax tree or document object model that it then serializes to JSON.
Data access #
While the application stores data in SQL Server, it uses no object-relational mapper (ORM). Instead, it simply uses ADO.NET, as also outlined in the article Do ORMs reduce the need for mapping?
At first glance, the Create method looks simple:
public async Task Create(Guid id, Table table) { using var conn = new SqlConnection(connectionString); using var cmd = table.Accept(new SqlInsertCommandVisitor(id)); cmd.Connection = conn; await conn.OpenAsync().ConfigureAwait(false); await cmd.ExecuteNonQueryAsync().ConfigureAwait(false); }
The main work, however, is done by the nested SqlInsertCommandVisitor class:
private sealed class SqlInsertCommandVisitor(Guid id) : ITableVisitor<SqlCommand> { public SqlCommand VisitCommunal(NaturalNumber capacity) { const string createCommunalSql = @" INSERT INTO [dbo].[Tables] ([PublicId], [Capacity]) VALUES (@PublicId, @Capacity)"; var cmd = new SqlCommand(createCommunalSql); cmd.Parameters.AddWithValue("@PublicId", id); cmd.Parameters.AddWithValue("@Capacity", (int)capacity); return cmd; } public SqlCommand VisitSingle(NaturalNumber capacity, NaturalNumber minimalReservation) { const string createSingleSql = @" INSERT INTO [dbo].[Tables] ([PublicId], [Capacity], [MinimalReservation]) VALUES (@PublicId, @Capacity, @MinimalReservation)"; var cmd = new SqlCommand(createSingleSql); cmd.Parameters.AddWithValue("@PublicId", id); cmd.Parameters.AddWithValue("@Capacity", (int)capacity); cmd.Parameters.AddWithValue("@MinimalReservation", (int)minimalReservation); return cmd; } }
It 'pattern-matches' on the two possible kinds of table and returns an appropriate SqlCommand that the Create method then executes. Notice that no 'Entity' class is needed. The code works straight on SqlCommand.
The same is true for the repository's Read method:
public async Task<Table?> Read(Guid id) { const string readByIdSql = @" SELECT [Capacity], [MinimalReservation] FROM [dbo].[Tables] WHERE[PublicId] = @id"; using var conn = new SqlConnection(connectionString); using var cmd = new SqlCommand(readByIdSql, conn); cmd.Parameters.AddWithValue("@id", id); await conn.OpenAsync().ConfigureAwait(false); using var rdr = await cmd.ExecuteReaderAsync().ConfigureAwait(false); if (!await rdr.ReadAsync().ConfigureAwait(false)) return null; var capacity = (int)rdr["Capacity"]; var mimimalReservation = rdr["MinimalReservation"] as int?; if (mimimalReservation is null) return Table.TryCreateCommunal(capacity); else return Table.TryCreateSingle(capacity, mimimalReservation.Value); }
It works directly on SqlDataReader. Again, no extra 'Entity' class is required. If the data in the database makes sense, the Read method return a well-encapsulated Table object.
XML formats #
That covers the basics, but how well does this kind of architecture stand up to changing requirements?
One axis of variation is when a service needs to support multiple representations. In this example, I'll imagine that the service also needs to support not just one, but two, XML formats.
Granted, you may not run into that particular requirement that often, but it's typical of a kind of change that you're likely to run into. In REST APIs, for example, you should use content negotiation for versioning, and that's the same kind of problem.
To be fair, application code also changes for a variety of other reasons, including new features, changes to business logic, etc. I can't possibly cover all, though, and many of these are much better described than changes in wire formats.
As described in the introduction article, ideally the XML should support a format implied by these examples:
<communal-table> <capacity>12</capacity> </communal-table> <single-table> <capacity>4</capacity> <minimal-reservation>3</minimal-reservation> </single-table>
Notice that while these two examples have different root elements, they're still considered to both represent a table. Although at the boundaries, static types are illusory we may still, loosely speaking, consider both of those XML documents as belonging to the same 'type'.
With both of the previous architectures described in this article series, I've had to give up on this schema. The present data architecture, finally, is able to handle this requirement.
HTTP interactions with element-biased XML #
The service should support the new XML format when presented with the the "application/xml" media type, either as a content-type header or accept header. An initial POST request may look like this:
POST /tables HTTP/1.1 content-type: application/xml <communal-table><capacity>12</capacity></communal-table>
Which produces a reply like this:
HTTP/1.1 201 Created Location: https://example.com/Tables/a77ac3fd221e4a5caaca3a0fc2b83ffc
And just like before, a client can later use the address in the Location header to request the resource. By using the accept header, it can indicate that it wishes to receive the reply formatted as XML:
GET /Tables/a77ac3fd221e4a5caaca3a0fc2b83ffc HTTP/1.1 accept: application/xml
Which produces this response with XML content in the body:
HTTP/1.1 200 OK Content-Type: application/xml; charset=utf-8 <communal-table><capacity>12</capacity></communal-table>
How do you add support for this new format?
Element-biased XML formatters #
Not surprisingly, you can add support for the new format by adding new formatters.
opts.InputFormatters.Add(new ElementBiasedTableXmlInputFormatter()); opts.OutputFormatters.Add(new ElementBiasedTableXmlOutputFormatter());
Importantly, and in stark contrast to the DTO-based Ports and Adapters example, you don't have to change the existing code to add XML support. If you're concerned about design heuristics such as the Single Responsibility Principle, you may consider this a win. Apart from the two lines of code adding the formatters, all other code to support this new feature is in new classes.
Both of the new formatters support the "application/xml" media type.
Deserializing element-biased XML #
The constructor and CanReadType implementation of ElementBiasedTableXmlInputFormatter is nearly identical to code you've already seen here, so I'll skip the repetition. The ReadRequestBodyAsync implementation is also conceptually similar, but of course differs in the details.
public override async Task<InputFormatterResult> ReadRequestBodyAsync( InputFormatterContext context, Encoding encoding) { var xml = await XElement .LoadAsync(context.HttpContext.Request.Body, LoadOptions.None, CancellationToken.None) .ConfigureAwait(false); var table = TableXml.TryParseElementBiased(xml); if (table is { }) return await InputFormatterResult.SuccessAsync(table).ConfigureAwait(false); else return await InputFormatterResult.FailureAsync().ConfigureAwait(false); }
As is also the case with the JSON input formatter, the ReadRequestBodyAsync method really only implements an Adapter over a more specialized parser function:
internal static Table? TryParseElementBiased(XElement xml) { if (xml.Name == "communal-table") { var capacity = xml.Element("capacity")?.Value; if (capacity is { }) { if (int.TryParse(capacity, out var c)) return Table.TryCreateCommunal(c); } } if (xml.Name == "single-table") { var capacity = xml.Element("capacity")?.Value; var minimalReservation = xml.Element("minimal-reservation")?.Value; if (capacity is { } && minimalReservation is { }) { if (int.TryParse(capacity, out var c) && int.TryParse(minimalReservation, out var mr)) return Table.TryCreateSingle(c, mr); } } return null; }
In keeping with the common theme of the Domain Model Only data architecture, it deserialized by examining an Abstract Syntax Tree (AST) or document object model (DOM), specifically making use of the XElement API. This class is really part of the LINQ to XML API, but you'll probably agree that the above code example makes little use of LINQ.
Serializing element-biased XML #
Hardly surprising, turning a Table object into element-biased XML involves steps similar to converting it to JSON. The ElementBiasedTableXmlOutputFormatter class' WriteResponseBodyAsync method contains this implementation:
public override Task WriteResponseBodyAsync( OutputFormatterWriteContext context, Encoding selectedEncoding) { if (context.Object is Table table) return context.HttpContext.Response.WriteAsync( table.GenerateElementBiasedXml(), selectedEncoding); throw new InvalidOperationException("Expected a Table object."); }
Again, the heavy lifting is done by a specialized function:
internal static string GenerateElementBiasedXml(this Table table) { return table.Accept(new ElementBiasedTableVisitor()); } private sealed class ElementBiasedTableVisitor : ITableVisitor<string> { public string VisitCommunal(NaturalNumber capacity) { var xml = new XElement( "communal-table", new XElement("capacity", (int)capacity)); return xml.ToString(SaveOptions.DisableFormatting); } public string VisitSingle( NaturalNumber capacity, NaturalNumber minimalReservation) { var xml = new XElement( "single-table", new XElement("capacity", (int)capacity), new XElement("minimal-reservation", (int)minimalReservation)); return xml.ToString(SaveOptions.DisableFormatting); } }
True to form, GenerateElementBiasedXml assembles an appropriate AST for the kind of table in question, and finally converts it to a string value.
Attribute-biased XML #
I was curious how far I could take this kind of variation, so for the sake of exploration, I invented yet another XML format to support. Instead of making exclusive use of XML elements, this format uses XML attributes for primitive values.
<communal-table capacity="12" /> <single-table capacity="4" minimal-reservation="3" />
In order to distinguish this XML format from the other, I invented the vendor media type "application/vnd.ploeh.table+xml". The new formatters only handle this media type.
There's not much new to report. The new formatters work like the previous. In order to parse the new format, a new function does that, still based on XElement:
internal static Table? TryParseAttributeBiased(XElement xml) { if (xml.Name == "communal-table") { var capacity = xml.Attribute("capacity")?.Value; if (capacity is { }) { if (int.TryParse(capacity, out var c)) return Table.TryCreateCommunal(c); } } if (xml.Name == "single-table") { var capacity = xml.Attribute("capacity")?.Value; var minimalReservation = xml.Attribute("minimal-reservation")?.Value; if (capacity is { } && minimalReservation is { }) { if (int.TryParse(capacity, out var c) && int.TryParse(minimalReservation, out var mr)) return Table.TryCreateSingle(c, mr); } } return null; }
Likewise, converting a Table object to this format looks like code you've already seen:
internal static string GenerateAttributeBiasedXml(this Table table) { return table.Accept(new AttributedBiasedTableVisitor()); } private sealed class AttributedBiasedTableVisitor : ITableVisitor<string> { public string VisitCommunal(NaturalNumber capacity) { var xml = new XElement( "communal-table", new XAttribute("capacity", (int)capacity)); return xml.ToString(SaveOptions.DisableFormatting); } public string VisitSingle( NaturalNumber capacity, NaturalNumber minimalReservation) { var xml = new XElement( "single-table", new XAttribute("capacity", (int)capacity), new XAttribute("minimal-reservation", (int)minimalReservation)); return xml.ToString(SaveOptions.DisableFormatting); } }
Consistent with adding the first XML support, I didn't have to touch any of the existing Controller or data access code.
Evaluation #
If you're concerned with separation of concerns, the Domain Model Only architecture gracefully handles variation in external formats without impacting application logic, Domain Model, or data access. You deal with each new format in a consistent and independent manner. The architecture offers the ultimate data representation flexibility, since everything you can write as a stream of bytes you can implement.
Since at the boundary, static types are illusory this architecture is congruent with reality. For a REST service, at least, reality is what goes on the wire. While static types can also be used to model what wire formats look like, there's always a risk that you can use your IDE's refactoring tools to change a DTO in such a way that the code still compiles, but you've now changed the wire format. This could easily break existing clients.
When wire compatibility is important, I test-drive enough self-hosted tests that directly use and verify the wire format to give me a good sense of stability. Without DTO classes, it becomes increasingly important to cover externally visible behaviour with a trustworthy test suite, but really, if compatibility is important, you should be doing that anyway.
It almost goes without saying that a requirement for this architecture is that your chosen web framework supports it. As you've seen here, ASP.NET does, but that's not a given in general. Most web frameworks worth their salt will come with mechanisms that enable you to add new wire formats, but the question is how opinionated such extensibility points are. Do they expect you to work with DTOs, or are they more flexible than that?
You may consider the pure Domain Model Only data architecture too specialized for everyday use. I may do that, too. As I wrote in the introduction article, I don't intent these walk-throughs to be prescriptive. Rather, they explore what's possible, so that you and I have a bigger set of alternatives to choose from.
Hybrid architectures #
In the code base that accompanies Code That Fits in Your Head, I use a hybrid data architecture that I've used for years. ADO.NET for data access, as shown here, but DTOs for external JSON serialization. As demonstrated in the article Using Ports and Adapters to persist restaurant table configurations, using DTOs for the presentation layer may cause trouble if you need to support multiple wire formats. On the other hand, if you don't expect that this is a concern, you may decide to run that risk. I often do that.
When presenting these three architectures to a larger audience, one audience member told me that his team used another hybrid architecture: DTOs for the presentation layer, and separate DTOs for data access, but no Domain Model. I can see how this makes sense in a mostly CRUD-heavy application where nonetheless you need to be able to vary user interfaces independently from the database schema.
Finally, I should point out that the Domain Model Only data architecture is, in reality, also a kind of Ports and Adapters architecture. It just uses more low-level Adapter implementations than you idiomatically see.
Conclusion #
The Domain Model Only data architecture emphasises modelling business logic as a strongly-typed, well-encapsulated Domain Model, while eschewing using statically-typed DTOs for communication with external processes. What I most like about this alternative is that it leaves little confusion as to where functionality goes.
When you have, say, TableDto, Table, and TableEntity classes, you need a sophisticated and mature team to trust all developers to add functionality in the right place. If there's only a single Table Domain Model, it may be more evident to developers that only business logic belongs there, and other concerns ought to be addressed in different ways.
Even so, you may consider all the low-level parsing code not to your liking, and instead decide to use DTOs. I may too, depending on context.
Comments
In this version of the data archictecture, let's suppose that the controller that now accepts a Domain Object directly is part of a larger REST API. How would you handle discoverability of the API, as the usual OpenAPI (Swagger et.al.) tools probably takes offence at this type of request object?
Jes, thank you for writing. If by discoverability you mean 'documentation', I would handle that the same way I usually handle documentation requirements for REST APIs: by writing one or my documents that explain how the API works. If there are other possible uses of OpenAPI than that, and the GUI to perform ad-hoc experiments, I'm going to need to be taken to task, because then I'm not aware of them.
I've recently discussed my general misgivings about OpenAPI, and they apply here as well. I'm aware that other people feel differently about this, and that's okay too.
"the usual OpenAPI (Swagger et.al.) tools probably takes offence at this type of request object"
You may be right, but I haven't tried, so I don't know if this is the case.
Using a Shared Data Model to persist restaurant table configurations
A data architecture example in C# and ASP.NET.
This is part of a small article series on data architectures. In this, the second instalment, you'll see a common attempt at addressing the mapping issue that I mentioned in the previous article. As the introductory article explains, the example code shows how to create a new restaurant table configuration, or how to display an existing resource. The sample code base is an ASP.NET 8.0 REST API.
Keep in mind that while the sample code does store data in a relational database, the term table in this article mainly refers to physical tables, rather than database tables.
The idea in this data architecture is to use a single, shared data model for each business object in the service. This is in contrast to the Ports and Adapters architecture, where you typically have a Data Transfer Object (DTO) for (JSON or XML) serialization, another class for the Domain Model, and a third to support an object-relational mapper.
An architecture diagram may attempt to illustrate the idea like this:
While ostensibly keeping alive the idea of application layers, data models are allowed to cross layers to be used both for database persistence, business logic, and in the presentation layer.
Data model #
Since the goal is to use a single class to model all application concerns, it means that we also need to use it for database persistence. The most commonly used ORM in .NET is Entity Framework, so I'll use that for the example. It's not something that I normally do, so it's possible that I could have done it better than what follows.
Still, assume that the database schema defines the Tables table like this:
CREATE TABLE [dbo].[Tables] ( [Id] INT NOT NULL IDENTITY PRIMARY KEY, [PublicId] UNIQUEIDENTIFIER NOT NULL UNIQUE, [Capacity] INT NOT NULL, [MinimalReservation] INT NULL )
I used a scaffolding tool to generate Entity Framework code from the database schema and then modified what it had created. This is the result:
public partial class Table { [JsonIgnore] public int Id { get; set; } [JsonIgnore] public Guid PublicId { get; set; } public string Type => MinimalReservation.HasValue ? "single" : "communal"; public int Capacity { get; set; } public int? MinimalReservation { get; set; } }
Notice that I added [JsonIgnore] attributes to two of the properties, since I didn't want to serialize them to JSON. I also added the calculated property Type to include a discriminator in the JSON documents.
HTTP interaction #
A client can create a new table with a POST HTTP request:
POST /tables HTTP/1.1
content-type: application/json
{"type":"communal","capacity":12}
Notice that the JSON document doesn't follow the desired schema described in the introduction article. It can't, because the data architecture is bound to the shared Table class. Or at least, if it's possible to attain the desired format with a single class and only some strategically placed attributes, I'm not aware of it. As the article Using only a Domain Model to persist restaurant table configurations will show, it is possible to attain that goal with the appropriate middleware, but I consider doing that to be an example of the third architecture, so not something I will cover in this article.
The service will respond to the above request like this:
HTTP/1.1 201 Created Location: https://example.com/Tables/777779466d2549d69f7e30b6c35bde3c
Clients can later use the address indicated by the Location header to retrieve a representation of the resource:
GET /Tables/777779466d2549d69f7e30b6c35bde3c HTTP/1.1 accept: application/json
Which elicits this response:
HTTP/1.1 200 OK
Content-Type: application/json; charset=utf-8
{"type":"communal","capacity":12}
The JSON format still doesn't conform to the desired format because the Controller in question deals exclusively with the shared Table data model.
Boundary #
At the boundary of the application, Controllers handle HTTP requests with action methods (an ASP.NET term). The framework matches requests by a combination of naming conventions and attributes. The Post action method handles incoming POST requests.
[HttpPost] public async Task<IActionResult> Post(Table table) { var id = Guid.NewGuid(); await repository.Create(id, table).ConfigureAwait(false); return new CreatedAtActionResult( nameof(Get), null, new { id = id.ToString("N") }, null); }
Notice that the input parameter isn't a separate DTO, but rather the shared Table object. Since it's shared, the Controller can pass it directly to the repository without any mapping.
The same simplicity is on display in the Get method:
[HttpGet("{id}")] public async Task<IActionResult> Get(string id) { if (!Guid.TryParseExact(id, "N", out var guid)) return new BadRequestResult(); Table? table = await repository.Read(guid).ConfigureAwait(false); if (table is null) return new NotFoundResult(); return new OkObjectResult(table); }
Once the Get method has parsed the id it goes straight to the repository, retrieves the table and returns it if it's there. No mapping is required by the Controller. What about the repository?
Data access #
The SqlTablesRepository class reads and writes data from SQL Server using Entity Framework. The Create method is as simple as this:
public async Task Create(Guid id, Table table) { ArgumentNullException.ThrowIfNull(table); table.PublicId = id; await context.Tables.AddAsync(table).ConfigureAwait(false); await context.SaveChangesAsync().ConfigureAwait(false); }
The Read method is even simpler - a one-liner:
public async Task<Table?> Read(Guid id) { return await context.Tables .SingleOrDefaultAsync(t => t.PublicId == id).ConfigureAwait(false); }
Again, no mapping. Just return the database Entity.
XML serialization #
Simple, so far, but how does this data architecture handle changing requirements?
One axis of variation is when a service needs to support multiple representations. In this example, I'll imagine that the service also needs to support XML.
Granted, you may not run into that particular requirement that often, but it's typical of a kind of change that you're likely to run into. In REST APIs, for example, you should use content negotiation for versioning, and that's the same kind of problem.
To be fair, application code also changes for a variety of other reasons, including new features, changes to business logic, etc. I can't possibly cover all, though, and many of these are much better described than changes in wire formats.
As was also the case in the previous article, it quickly turns out that it's not possible to support any of the desired XML formats described in the introduction article. Instead, for the sake of exploring what is possible, I'll compromise and support XML documents like these examples:
<table> <type>communal</type> <capacity>12</capacity> </table> <table> <type>single</type> <capacity>4</capacity> <minimal-reservation>3</minimal-reservation> </table>
This schema, it turns out, is the same as the element-biased format from the previous article. I could, instead, have chosen to support the attribute-biased format, but, because of the shared data model, not both.
Notice how using statically typed classes, attributes, and Reflection to guide serialization leads toward certain kinds of formats. You can't easily support any arbitrary JSON or XML schema, but are rather nudged into a more constrained subset of possible formats. There's nothing too bad about this. As usual, there are trade-offs involved. You concede flexibility, but gain convenience: Just slab some attributes on your DTO, and it works well enough for most purposes. I mostly point it out because this entire article series is about awareness of choice. There's always some cost to be paid.
That said, supporting that XML format is surprisingly easy:
[XmlRoot("table")] public partial class Table { [JsonIgnore, XmlIgnore] public int Id { get; set; } [JsonIgnore, XmlIgnore] public Guid PublicId { get; set; } [XmlElement("type"), NotMapped] public string? Type { get; set; } [XmlElement("capacity")] public int Capacity { get; set; } [XmlElement("minimal-reservation")] public int? MinimalReservation { get; set; } public bool ShouldSerializeMinimalReservation() => MinimalReservation.HasValue; internal void InferType() { Type = MinimalReservation.HasValue ? "single" : "communal"; } }
Most of the changes are simple additions of the XmlRoot, XmlElement, and XmlIgnore attributes. In order to serialize the <type> element, however, I also had to convert the Type property to a read/write property, which had some ripple effects.
For one, I had to add the NotMapped attribute to tell Entity Framework that it shouldn't try to save the value of that property in the database. As you can see in the above SQL schema, the Tables table has no Type column.
This also meant that I had to change the Read method in SqlTablesRepository to call the new InferType method:
public async Task<Table?> Read(Guid id) { var table = await context.Tables .SingleOrDefaultAsync(t => t.PublicId == id).ConfigureAwait(false); table?.InferType(); return table; }
I'm not happy with this kind of sequential coupling, but to be honest, this data architecture inherently has an appalling lack of encapsulation. Having to call InferType is just par for the course.
That said, despite a few stumbling blocks, adding XML support turned out to be surprisingly easy in this data architecture. Granted, I had to compromise on the schema, and could only support one XML schema, so we shouldn't really take this as an endorsement. To paraphrase Gerald Weinberg, if it doesn't have to work, it's easy to implement.
Evaluation #
There's no denying that the Shared Data Model architecture is simple. There's no mapping between different layers, and it's easy to get started. Like the DTO-based Ports and Adapters architecture, you'll find many documentation examples and getting-started guides that work like this. In a sense, you can say that it's what the ASP.NET framework, or, perhaps particularly the Entity Framework (EF), 'wants you to do'. To be fair, I find ASP.NET to be reasonably unopinionated, so what inveigling you may run into may be mostly attributable to EF.
While it may feel nice that it's easy to get started, instant gratification often comes at a cost. Consider the Table class shown here. Because of various constraints imposed by EF and the JSON and XML serializers, it has no encapsulation. One thing is that the sophisticated Visitor-encoded Table class introduced in the article Serializing restaurant tables in C# is completely out of the question, but you can't even add a required constructor like this one:
public Table(int capacity) { Capacity = capacity; }
Granted, it seems to work with both EF and the JSON serializer, which I suppose is a recent development, but it doesn't work with the XML serializer, which requires that
"A class must have a parameterless constructor to be serialized by XmlSerializer."
Even if this, too, changes in the future, DTO-based designs are at odds with encapsulation. If you doubt the veracity of that statement, I challenge you to complete the Priority Collection kata with serializable DTOs.
Another problem with the Shared Data Model architecture is that it so easily decays to a Big Ball of Mud. Even though the above architecture diagram hollowly insists that layering is still possible, a Shared Data Model is an attractor of behaviour. You'll soon find that a class like Table has methods that serve presentation concerns, others that implement business logic, and others again that address persistence issues. It has become a God Class.
From these problems it doesn't follow that the architecture doesn't have merit. If you're developing a CRUD-heavy application with a user interface (UI) that's merely a glorified table view, this could be a good choice. You would be coupling the UI to the database, so that if you need to change how the UI works, you might also have to modify the database schema, or vice versa.
This is still not an indictment, but merely an observation of consequences. If you can live with them, then choose the Shared Data Model architecture. I can easily imagine application types where that would be the case.
Conclusion #
In the Shared Data Model architecture you use a single model (here, a class) to handle all application concerns: UI, business logic, data access. While this shows a blatant disregard for the notion of separation of concerns, no law states that you must, always, separate concerns.
Sometimes it's okay to mix concerns, and then the Shared Data Model architecture is dead simple. Just make sure that you know when it's okay.
While this architecture is the ultimate in simplicity, it's also quite constrained. The third and final data architecture I'll cover, on the other hand, offers the ultimate in flexibility, at the expense (not surprisingly) of some complexity.
Next: Using only a Domain Model to persist restaurant table configurations.
Using Ports and Adapters to persist restaurant table configurations
A data architecture example in C# and ASP.NET.
This is part of a small article series on data architectures. In the first instalment, you'll see the outline of a Ports and Adapters implementation. As the introductory article explains, the example code shows how to create a new restaurant table configuration, or how to display an existing resource. The sample code base is an ASP.NET 8.0 REST API.
Keep in mind that while the sample code does store data in a relational database, the term table in this article mainly refers to physical tables, rather than database tables.
While Ports and Adapters architecture diagrams are usually drawn as concentric circles, you can also draw (subsets of) it as more traditional layered diagrams:
Here, the arrows indicate mappings, not dependencies.
HTTP interaction #
A client can create a new table with a POST HTTP request:
POST /tables HTTP/1.1
content-type: application/json
{ "communalTable": { "capacity": 16 } }
Which might elicit a response like this:
HTTP/1.1 201 Created Location: https://example.com/Tables/844581613e164813aa17243ff8b847af
Clients can later use the address indicated by the Location header to retrieve a representation of the resource:
GET /Tables/844581613e164813aa17243ff8b847af HTTP/1.1 accept: application/json
Which would result in this response:
HTTP/1.1 200 OK
Content-Type: application/json; charset=utf-8
{"communalTable":{"capacity":16}}
By default, ASP.NET handles and returns JSON. Later in this article you'll see how well it deals with other data formats.
Boundary #
ASP.NET supports some variation of the model-view-controller (MVC) pattern, and Controllers handle HTTP requests. At the outset, the action method that handles the POST request looks like this:
[HttpPost] public async Task<IActionResult> Post(TableDto dto) { ArgumentNullException.ThrowIfNull(dto); var id = Guid.NewGuid(); await repository.Create(id, dto.ToTable()).ConfigureAwait(false); return new CreatedAtActionResult(nameof(Get), null, new { id = id.ToString("N") }, null); }
As is idiomatic in ASP.NET, input and output are modelled by data transfer objects (DTOs), in this case called TableDto. I've already covered this little object model in the article Serializing restaurant tables in C#, so I'm not going to repeat it here.
The ToTable method, on the other hand, is a good example of how trying to cut corners lead to more complicated code:
internal Table ToTable() { var candidate = Table.TryCreateSingle(SingleTable?.Capacity ?? -1, SingleTable?.MinimalReservation ?? -1); if (candidate is { }) return candidate.Value; candidate = Table.TryCreateCommunal(CommunalTable?.Capacity ?? -1); if (candidate is { }) return candidate.Value; throw new InvalidOperationException("Invalid TableDto."); }
Compare it to the TryParse method in the Serializing restaurant tables in C# article. That one is simpler, and less error-prone.
I think that I wrote ToTable that way because I didn't want to deal with error handling in the Controller, and while I test-drove the code, I never wrote a test that supply malformed input. I should have, and so should you, but this is demo code, and I never got around to it.
Enough about that. The other action method handles GET requests:
[HttpGet("{id}")] public async Task<IActionResult> Get(string id) { if (!Guid.TryParseExact(id, "N", out var guid)) return new BadRequestResult(); var table = await repository.Read(guid).ConfigureAwait(false); if (table is null) return new NotFoundResult(); return new OkObjectResult(TableDto.From(table.Value)); }
The static TableDto.From method is identical to the ToDto method from the Serializing restaurant tables in C# article, just with a different name.
To summarize so far: At the boundary of the application, Controller methods receive or return TableDto objects, which are mapped to and from the Domain Model named Table.
Domain Model #
The Domain Model Table is also identical to the code shown in Serializing restaurant tables in C#. In order to comply with the Dependency Inversion Principle (DIP), mapping to and from TableDto is defined on the latter. The DTO, being an implementation detail, may depend on the abstraction (the Domain Model), but not the other way around.
In the same spirit, conversions to and from the database are defined entirely within the repository implementation.
Data access layer #
Keeping the example consistent, the code base also models data access with C# classes. It uses Entity Framework to read from and write to SQL Server. The class that models a row in the database is also a kind of DTO, even though here it's idiomatically called an entity:
public partial class TableEntity { public int Id { get; set; } public Guid PublicId { get; set; } public int Capacity { get; set; } public int? MinimalReservation { get; set; } }
I had a command-line tool scaffold the code for me, and since I don't usually live in that world, I don't know why it's a partial class. It seems to be working, though.
The SqlTablesRepository class implements the mapping between Table and TableEntity. For instance, the Create method looks like this:
public async Task Create(Guid id, Table table) { var entity = table.Accept(new TableToEntityConverter(id)); await context.Tables.AddAsync(entity).ConfigureAwait(false); await context.SaveChangesAsync().ConfigureAwait(false); }
That looks simple, but is only because all the work is done by the TableToEntityConverter, which is a nested class:
private sealed class TableToEntityConverter : ITableVisitor<TableEntity> { private readonly Guid id; public TableToEntityConverter(Guid id) { this.id = id; } public TableEntity VisitCommunal(NaturalNumber capacity) { return new TableEntity { PublicId = id, Capacity = (int)capacity, }; } public TableEntity VisitSingle( NaturalNumber capacity, NaturalNumber minimalReservation) { return new TableEntity { PublicId = id, Capacity = (int)capacity, MinimalReservation = (int)minimalReservation, }; } }
Mapping the other way is easier, so the SqlTablesRepository does it inline in the Read method:
public async Task<Table?> Read(Guid id) { var entity = await context.Tables .SingleOrDefaultAsync(t => t.PublicId == id).ConfigureAwait(false); if (entity is null) return null; if (entity.MinimalReservation is null) return Table.TryCreateCommunal(entity.Capacity); else return Table.TryCreateSingle( entity.Capacity, entity.MinimalReservation.Value); }
Similar to the case of the DTO, mapping between Table and TableEntity is the responsibility of the SqlTablesRepository class, since data persistence is an implementation detail. According to the DIP it shouldn't be part of the Domain Model, and it isn't.
XML formats #
That covers the basics, but how well does this kind of architecture stand up to changing requirements?
One axis of variation is when a service needs to support multiple representations. In this example, I'll imagine that the service also needs to support not just one, but two, XML formats.
Granted, you may not run into that particular requirement that often, but it's typical of a kind of change that you're likely to run into. In REST APIs, for example, you should use content negotiation for versioning, and that's the same kind of problem.
To be fair, application code also changes for a variety of other reasons, including new features, changes to business logic, etc. I can't possibly cover all, though, and many of these are much better described than changes in wire formats.
As described in the introduction article, ideally the XML should support a format implied by these examples:
<communal-table> <capacity>12</capacity> </communal-table> <single-table> <capacity>4</capacity> <minimal-reservation>3</minimal-reservation> </single-table>
Notice that while these two examples have different root elements, they're still considered to both represent a table. Although at the boundaries, static types are illusory we may still, loosely speaking, consider both of those XML documents as belonging to the same 'type'.
To be honest, if there's a way to support this kind of schema by defining DTOs to be serialized and deserialized, I don't know what it looks like. That's not meant to imply that it's impossible. There's often an epistemological problem associated with proving things impossible, so I'll just leave it there.
To be clear, it's not that I don't know how to support that kind of schema at all. I do, as the article Using only a Domain Model to persist restaurant table configurations will show. I just don't know how to do it with DTO-based serialisation.
Element-biased XML #
Instead of the above XML schema, I will, instead explore how hard it is to support a variant schema, implied by these two examples:
<table> <type>communal</type> <capacity>12</capacity> </table> <table> <type>single</type> <capacity>4</capacity> <minimal-reservation>3</minimal-reservation> </table>
This variation shares the same <table> root element and instead distinguishes between the two kinds of table with a <type> discriminator.
This kind of schema we can define with a DTO:
[XmlRoot("table")] public class ElementBiasedTableXmlDto { [XmlElement("type")] public string? Type { get; set; } [XmlElement("capacity")] public int Capacity { get; set; } [XmlElement("minimal-reservation")] public int? MinimalReservation { get; set; } public bool ShouldSerializeMinimalReservation() => MinimalReservation.HasValue; // Mapping methods not shown here... }
As you may have already noticed, however, this isn't the same type as TableJsonDto, so how are we going to implement the Controller methods that receive and send objects of this type?
Posting XML #
The service should still accept JSON as shown above, but now, additionally, it should also support HTTP requests like this one:
POST /tables HTTP/1.1 content-type: application/xml <table><type>communal</type><capacity>12</capacity></table>
How do you implement this new feature?
My first thought was to add a Post overload to the Controller:
[HttpPost] public async Task<IActionResult> Post(ElementBiasedTableXmlDto dto) { ArgumentNullException.ThrowIfNull(dto); var id = Guid.NewGuid(); await repository.Create(id, dto.ToTable()).ConfigureAwait(false); return new CreatedAtActionResult( nameof(Get), null, new { id = id.ToString("N") }, null); }
I just copied and pasted the original Post method and changed the type of the dto parameter. I also had to add a ToTable conversion to ElementBiasedTableXmlDto:
internal Table ToTable() { if (Type == "single") { var t = Table.TryCreateSingle(Capacity, MinimalReservation ?? 0); if (t is { }) return t.Value; } if (Type == "communal") { var t = Table.TryCreateCommunal(Capacity); if (t is { }) return t.Value; } throw new InvalidOperationException("Invalid Table DTO."); }
While all of that compiles, it doesn't work.
When you attempt to POST a request against the service, the ASP.NET framework now throws an AmbiguousMatchException indicating that "The request matched multiple endpoints". Which is understandable.
This lead me to the first round of Framework Whac-A-Mole. What I'd like to do is to select the appropriate action method based on content-type or accept headers. How does one do that?
After some web searching, I came across a Stack Overflow answer that seemed to indicate a way forward.
Selecting the right action method #
One way to address the issue is to implement a custom ActionMethodSelectorAttribute:
public sealed class SelectTableActionMethodAttribute : ActionMethodSelectorAttribute { public override bool IsValidForRequest(RouteContext routeContext, ActionDescriptor action) { if (action is not ControllerActionDescriptor cad) return false; if (cad.Parameters.Count != 1) return false; var dtoType = cad.Parameters[0].ParameterType; // Demo code only. This doesn't take into account a possible charset // parameter. See RFC 9110, section 8.3 // (https://www.rfc-editor.org/rfc/rfc9110#field.content-type) for more // information. if (routeContext?.HttpContext.Request.ContentType == "application/json") return dtoType == typeof(TableJsonDto); if (routeContext?.HttpContext.Request.ContentType == "application/xml") return dtoType == typeof(ElementBiasedTableXmlDto); return false; } }
As the code comment suggests, this isn't as robust as it should be. A content-type header may also look like this:
Content-Type: application/json; charset=utf-8
The exact string equality check shown above would fail in such a scenario, suggesting that a more sophisticated implementation is warranted. I'll skip that for now, since this demo code already compromises on the overall XML schema. For an example of more robust content negotiation implementations, see Using only a Domain Model to persist restaurant table configurations.
Adorn both Post action methods with this custom attribute, and the service now handles both formats:
[HttpPost, SelectTableActionMethod] public async Task<IActionResult> Post(TableJsonDto dto) // ... [HttpPost, SelectTableActionMethod] public async Task<IActionResult> Post(ElementBiasedTableXmlDto dto) // ...
While that handles POST requests, it doesn't implement content negotiation for GET requests.
Getting XML #
In order to GET an XML representation, clients can supply an accept header value:
GET /Tables/153f224c91fb4403988934118cc14024 HTTP/1.1 accept: application/xml
which will reply with
HTTP/1.1 200 OK Content-Length: 59 Content-Type: application/xml; charset=utf-8 <table><type>communal</type><capacity>12</capacity></table>
How do we implement that?
Keep in mind that since this data-architecture variation uses two different DTOs to model JSON and XML, respectively, an action method can't just return an object of a single type and hope that the ASP.NET framework takes care of the rest. Again, I'm aware of middleware that'll deal nicely with this kind of problem, but not in this architecture; see Using only a Domain Model to persist restaurant table configurations for such a solution.
The best I could come up with, given the constraints I'd imposed on myself, then, was this:
[HttpGet("{id}")] public async Task<IActionResult> Get(string id) { if (!Guid.TryParseExact(id, "N", out var guid)) return new BadRequestResult(); var table = await repository.Read(guid).ConfigureAwait(false); if (table is null) return new NotFoundResult(); // Demo code only. This doesn't take into account quality values. var accept = httpContextAccessor?.HttpContext?.Request.Headers.Accept.ToString(); if (accept == "application/json") return new OkObjectResult(TableJsonDto.From(table.Value)); if (accept == "application/xml") return new OkObjectResult(ElementBiasedTableXmlDto.From(table.Value)); return new StatusCodeResult((int)HttpStatusCode.NotAcceptable); }
As the comment suggests, this is once again code that barely passes the few tests that I have, but really isn't production-ready. An accept header may also look like this:
accept: application/xml; q=1.0,application/json; q=0.5
Given such an accept header, the service ought to return an XML representation with the application/xml content type, but instead, this Get method returns 406 Not Acceptable.
As I've already outlined, I'm not going to fix this problem, as this is only an exploration. It seems that we can already conclude that this style of architecture is ill-suited to deal with this kind of problem. If that's the conclusion, then why spend time fixing outstanding problems?
Attribute-biased XML #
Even so, just to punish myself, apparently, I also tried to add support for an alternative XML format that use attributes to record primitive values. Again, I couldn't make the schema described in the introductory article work, but I did manage to add support for XML documents like these:
<table type="communal" capacity="12" /> <table type="single" capacity="4" minimal-reservation="3" />
The code is similar to what I've already shown, so I'll only list the DTO:
[XmlRoot("table")] public class AttributeBiasedTableXmlDto { [XmlAttribute("type")] public string? Type { get; set; } [XmlAttribute("capacity")] public int Capacity { get; set; } [XmlAttribute("minimal-reservation")] public int MinimalReservation { get; set; } public bool ShouldSerializeMinimalReservation() => 0 < MinimalReservation; // Mapping methods not shown here... }
This DTO looks a lot like the ElementBiasedTableXmlDto class, only it adorns properties with XmlAttribute rather than XmlElement.
Evaluation #
Even though I had to compromise on essential goals, I wasted an appalling amount of time and energy on yak shaving and Framework Whac-A-Mole. The DTO-based approach to modelling external resources really doesn't work when you need to do substantial content negotiation.
Even so, a DTO-based Ports and Adapters architecture may be useful when that's not a concern. If, instead of a REST API, you're developing a web site, you'll typically not need to vary representation independently of resource. In other words, a web page is likely to have at most one underlying model.
Compared to other large frameworks I've run into, ASP.NET is fairly unopinionated. Even so, the idiomatic way to use it is based on DTOs. DTOs to represent external data. DTOs to represent UI components. DTOs to represent database rows (although they're often called entities in that context). You'll find a ton of examples using this data architecture, so it's incredibly well-described. If you run into problems, odds are that someone has blazed a trail before you.
Even outside of .NET, this kind of architecture is well-known. While I've learned a thing or two from experience, I've picked up a lot of my knowledge about software architecture from people like Martin Fowler and Robert C. Martin.
When you also apply the Dependency Inversion Principle, you'll get good separations of concerns. This aspect of Ports and Adapters is most explicitly described in Clean Architecture. For example, a change to the UI generally doesn't affect the database. You may find that example ridiculous, because why should it, but consult the article Using a Shared Data Model to persist restaurant table configurations to see how this may happen.
The major drawbacks of the DTO-based data architecture is that much mapping is required. With three different DTOs (e.g. JSON DTO, Domain Model, and ORM Entity), you need four-way translation as indicated in the above figure. People often complain about all that mapping, and no: ORMs don't reduce the need for mapping.
Another problem is that this style of architecture is complicated. As I've argued elsewhere, Ports and Adapters often constitute an unstable equilibrium. While you can make it work, it requires a level of sophistication and maturity among team members that is not always present. And when it goes wrong, it may quickly deteriorate into a Big Ball of Mud.
Conclusion #
A DTO-based Ports and Adapters architecture is well-described and has good separation of concerns. In this article, however, we've seen that it doesn't deal successfully with realistic content negotiation. While that may seem like a shortcoming, it's a drawback that you may be able to live with. Particularly if you don't need to do content negotiation at all.
This way of organizing code around data is quite common. It's often the default data architecture, and I sometimes get the impression that a development team has 'chosen' to use it without considering alternatives.
It's not a bad architecture despite evidence to the contrary in this article. The scenario examined here may not be relevant. The main drawback of having all these objects playing different roles is all the mapping that's required.
The next data architecture attempts to address that concern.
Next: Using a Shared Data Model to persist restaurant table configurations.

Comments
Thanks for a nice blog post! I found the challange interesting, so I have written my own version of the code that both tries to be faster and also remove the redundant solutions, so it only generates two solutions in total. The code is available here. It executes in roughly 8 milliseconds both in ghci and compiled (and takes a second to compile and run using runghc) on my laptop.
In order to improve the performance, I start with a blank grid and one-by-one add tiles until it is no longer possible to do so, and then bactrack, kind of like how you would do it by hand. As a tiny bonus, that I haven't actually measured if it makes any practical difference, I also selected the order of filling in the grid so that they can constrain each other as much as possible, by filling 2-by-2 squares as early as possible. I have however calculated the number of boards explored in each of the two variations. With a spiral order, 6852 boards are explored, while with a linear order, 9332 boards are explored.
In order to eliminate rotational symmetry, I start by filling the center square and fixing its rotation, rather than trying all rotations for it, since we could view any initial rotation of the center square as equivalent to rotating the whole board. In order to eliminate the identical solutions from the two identical tiles, I changed the encoding to use a number next to the tile to say how many copies are left of it, so when we choose a tile, there is only a single way to choose each tile, even if there are multiple copies of it. Both of these would also in theory make the code slightly faster if the time wasn't already dominated by general IO and other unrelated things.
I also added various pretty printing and tracing utilites to the code, so you can see exactly how it executes and which partial solutions it explores.
Thank you for writing. I did try filling the two-by-two square first, as you suggest, but in isolation it makes no discernable difference.
I haven't tried your two other optimizations. The one to eliminate rotations should, I guess, reduce the search space to a fourth of mine, unless I'm mistaken. That would reduce my 300 ms to approximately 75 ms.
I can't easily guess how much time the other optimization shaves off, but it could be the one that makes the bigger difference.