ploeh blog danish software design
Boundaries are explicit
A reading of the first Don Box tenet, with some commentary.
This article is part of a series titled The four tenets of SOA revisited. In each of these articles, I'll pull one of Don Box's four tenets of service-oriented architecture (SOA) out of the original MSDN Magazine article and add some of my own commentary. If you're curious why I do that, I cover that in the introductory article.
In this article, I'll go over the first tenet, quoting from the MSDN Magazine article unless otherwise indicated.
Boundaries are explicit #
This tenet was the one I struggled with the most. It took me a long time to come to grips with how to apply it, but I'll get back to that in a moment. First, here's what the article said:
A service-oriented application often consists of services that are spread over large geographical distances, multiple trust authorities, and distinct execution environments. The cost of traversing these various boundaries is nontrivial in terms of complexity and performance. Service-oriented designs acknowledge these costs by putting a premium on boundary crossings. Because each cross-boundary communication is potentially costly, service-orientation is based on a model of explicit message passing rather than implicit method invocation. Compared to distributed objects, the service-oriented model views cross-service method invocation as a private implementation technique, not as a primitive construct—the fact that a given interaction may be implemented as a method call is a private implementation detail that is not visible outside the service boundary.
Though service-orientation does not impose the RPC-style notion of a network-wide call stack, it can support a strong notion of causality. It is common for messages to explicitly indicate which chain(s) of messages a particular message belongs to. This indication is useful for message correlation and for implementing several common concurrency models.
The notion that boundaries are explicit applies not only to inter-service communication but also to inter-developer communication. Even in scenarios in which all services are deployed in a single location, it is commonplace for the developers of each service to be spread across geographical, cultural, and/or organizational boundaries. Each of these boundaries increases the cost of communication between developers. Service orientation adapts to this model by reducing the number and complexity of abstractions that must be shared across service boundaries. By keeping the surface area of a service as small as possible, the interaction and communication between development organizations is reduced. One theme that is consistent in service-oriented designs is that simplicity and generality aren't a luxury but rather a critical survival skill.
Notice that there's nothing here about Windows Communication Framework (WCF), or any other specific technology. This is common to all four tenets, and one of the reasons that I think they deserve to be lifted out of their original context and put on display as the general ideas that they are.
I'm getting the vibe that the above description was written under the impression of the disenchantment with distributed objects that was setting in around that time. The year before, Martin Fowler had formulated his
"First Law of Distributed Object Design: Don't distribute your objects!"
The way that I read the tenet then, and the way I still read it today, is that in contrast to distributed objects, you should treat any service invocation as a noticeable operation, "putting a premium on boundary crossings", somehow distinct from normal code.
Perhaps I read to much into that, because WCF immediately proceeded to convert any SOAP service into a lot of auto-generated C# code that would then enable you to invoke operations on a remote service using (you guessed it) a method invocation.
Here a code snippet from the WCF documentation:
double value1 = 100.00D; double value2 = 15.99D; double result = client.Add(value1, value2);
What happens here is that client.Add creates and sends a SOAP message to a service, receives the response, unpacks it, and returns it as a double value. Even so, it looks just like any other method call. There's no "premium on boundary crossings" here.
So much for the principle that boundaries are explicit. They're not, and it bothered me twenty years ago, as it bothers me today.
I'll remind you what the problem is. When the boundary is not explicit, you may inadvertently write client code that makes network calls, and you may not be aware of it. This could noticeably slow down the application, particularly if you do it in a loop.
How do you make boundaries explicit? #
This problem isn't isolated to WCF or SOAP. Network calls are slow and unreliable. Perhaps you're connecting to a system on the other side of the Earth. Perhaps the system is unavailable. This is true regardless of protocol.
From the software architect's perspective, the tenet that boundaries are explicit is a really good idea. The clearer it is where in a code base network operations take place, the easier it is to troubleshot and maintain that code. This could make it easier to spot n + 1 problems, as well as give you opportunities to add logging, Circuit Breakers, etc.
How do you make boundaries explicit? Clearly, WCF failed to do so, despite the design goal.
Only Commands #
After having struggled with this question for years, I had an idea. This idea, however, doesn't really work, but I'll briefly cover it here. After all, if I can have that idea, other people may get it as well. It could save you some time if I explain why I believe that it doesn't address the problem.
The idea is to mandate that all network operations are Commands. In a C-like language, that would indicate a void method.
While it turns out that it ultimately doesn't work, this isn't just some arbitrary rule that I've invented. After all, if a method doesn't return anything, the boundary does, in a sense, become explicit. You can't just 'keep dotting', fluent-interface style.
channel.UpdateProduct(pc);
This gives you the opportunity to treat network operations as fire-and-forget operations. While you could still run such Commands in a tight loop, you could at least add them to a queue and move on. Such a queue could be be an in-process data structure, or a persistent queue. Your network card also holds a small queue of network packets.
This is essentially an asynchronous messaging architecture. It seems to correlate with Don Box's talk about messages.
Although this may seem as though it addresses some concerns about making boundaries explicit, an obvious question arises: How do you perform queries in this model?
You could keep such an architecture clean. You might, for example, implement a CQRS architecture where Commands create Events for which your application may subscribe. Such events could be handled by event handlers (other void methods) to update in-memory data as it changes.
Even so, there are practical limitations with such a model. What's likely to happen, instead, is the following.
Request-Reply #
It's hardly unlikely that you may need to perform some kind of Query against a remote system. If you can only communicate with services using void methods, such a scenario seems impossible.
It's not. There's even a pattern for that. Enterprise Integration Patterns call it Request-Reply. You create a Query message and give it a correlation ID, send it, and wait for the reply message to arrive at your own message handler. Client code might look like this:
var correlationId = Guid.NewGuid();
var query = new FavouriteSongsQuery(UserId: 123, correlationId);
channel.Send(query);
IReadOnlyCollection<Song> songs = [];
while (true)
{
var response = subscriber.GetNextResponse(correlationId);
if (response is null)
Thread.Sleep(100);
else
songs = response;
break;
}
While this works, it's awkward to use, so it doesn't take long before someone decides to wrap it in a helpful helper method:
public IReadOnlyCollection<Song> GetFavouriteSongs(int userId)
{
var correlationId = Guid.NewGuid();
var query = new FavouriteSongsQuery(userId, correlationId);
channel.Send(query);
IReadOnlyCollection<Song> songs = [];
while (true)
{
var response = subscriber.GetNextResponse(correlationId);
if (response is null)
Thread.Sleep(100);
else
songs = response;
break;
}
return songs;
}
This now enables you to write client code like this:
var songService = new SongService(); var songs = songService.GetFavouriteSongs(123);
We're back where we started. Boundaries are no longer explicit. Equivalent to how good names are only skin-deep, this attempt to make boundaries explicit can't resist programmers' natural tendency to make things easier for themselves.
If only there was some way to make an abstraction contagious...
Contagion #
Ideally, we'd like to make boundaries explicit in such a way that they can't be hidden away. After all,
"Abstraction is the elimination of the irrelevant and the amplification of the essential."
The existence of a boundary is essential, so while we might want to eliminate various other irrelevant details, this is a property that we should retain and surface in APIs. Even better, it'd be best if we could do it in such a way that it can't easily be swept under the rug, as shown above.
In Haskell, this is true for all input/output - not only network requests, but also file access, and other non-deterministic actions. In Haskell this is a 'wrapper' type called IO; for an explanation with C# examples, see The IO Container.
In a more idiomatic way, we can use task asynchronous programming as an IO surrogate. People often complain that async code is contagious. By that they mean that once a piece of code is asynchronous, the caller must also be asynchronous. This effect is transitive, and while this is often lamented as a problem, this is exactly what we need. Amplify the essential. Make boundaries explicit.
This doesn't mean that your entire code base has to be asynchronous. Only your network (and similar, non-deterministic) code should be asynchronous. Write your Domain Model and application code as pure functions, and compose them with the asynchronous code using standard combinators.
Conclusion #
The first of Don Box's four tenets of SOA is that boundaries should be explicit. WCF failed to deliver on that ideal, and it took me more than a decade to figure out how to square that circle.
Many languages now come with support for asynchronous programming, often utilizing some kind of generic Task or Async monad. Since such types are usually contagious, you can use them to make boundaries explicit.
Next: Services are autonomous.
The four tenets of SOA revisited
Twenty years after.
In the January 2004 issue of MSDN Magazine you can find an article by Don Box titled A Guide to Developing and Running Connected Systems with Indigo. Buried within the (now dated) discussion of the technology code-named Indigo (later Windows Communication Foundation) you can find a general discussion of four tenets of service-oriented architecture (SOA).
I remember that they resonated strongly with me back then, or that they at least prompted me to think explicitly about how to design software services. Some of these ideas have stayed with me ever since, while another has nagged at me for decades before I found a way to reconcile it with other principles of software design.
Now that it's twenty years ago that the MSDN article was published, I find that this is as good a time as ever to revisit it.
Legacy #
Why should we care about an old article about SOAP and SOA? Does anyone even use such things today, apart from legacy systems?
After all, we've moved on from SOAP to REST, gRPC, or GraphQL, and from SOA to microservices - that is, if we're not already swinging back towards monoliths.
Even so, I find much of what Don Box wrote twenty years ago surprisingly prescient. If you're interested in distributed software design involving some kind of remote API design, the four tenets of service-orientation apply beyond their original context. Some of the ideas, at least.
As is often the case in our field, various resources discuss the tenets without much regard to proper citation. Thus, I can't be sure that the MSDN article is where they first appeared, but I haven't found any earlier source.
My motivation for writing these article is partly to rescue the four tenets from obscurity, and partly to add some of my own commentary.
Much of the original article is about Indigo, and I'm going to skip that. On the other hand, I'm going to quote rather extensively from the article, in order to lift the more universal ideas out of their original context.
I'll do that in a series of articles, each covering one of the tenets.
- Boundaries are explicit
- Services are autonomous
- Services share schema and contract, not class
- Service compatibility is determined based on policy
Not all of the tenets have stood the test of time equally well, so I may not add an equal amount of commentary to all four.
Conclusion #
Ever since I first encountered the four tenets of SOA, they've stayed with me in one form or other. When helping teams to design services, even what we may today consider 'modern services', I've drawn on some of those ideas. There are insights of a general nature that are worth considering even today.
Next: Boundaries are explicit.
Testing exceptions
Some thoughts on testing past the happy path.
Test-driven development is a great development technique that enables you to get rapid feedback on design and implementation ideas. It enables you to rapidly move towards a working solution.
The emphasis on the happy path, however, can make you forget about all the things that may go wrong. Sooner or later, though, you may realize that the implementation can fail for a number of reasons, and, wanting to make things more robust, you may want to also subject your error-handling code to automated testing.
This doesn't have to be difficult, but can raise some interesting questions. In this article, I'll try to address a few.
Throwing exceptions with a dynamic mock #
In a question to another article AmirB asks how to use a Fake Object to test exceptions. Specifically, since a Fake is a Test Double with a coherent contract it'll be inappropriate to let it throw exceptions that relate to different implementations.
Egads, that was quite abstract, so let's consider a concrete example.
The original article that AmirB asked about used this interface as an example:
public interface IUserRepository { User Read(int userId); void Create(int userId); }
Granted, this interface is a little odd, but it should be good enough for the present purpose. As AmirB wrote:
"In scenarios where dynamic mocks (like Moq) are employed, we can mock a method to throw an exception, allowing us to test the expected behavior of the System Under Test (SUT)."
Specifically, this might look like this, using Moq:
[Fact] public void CreateThrows() { var td = new Mock<IUserRepository>(); td.Setup(r => r.Read(1234)).Returns(new User { Id = 0 }); td.Setup(r => r.Create(It.IsAny<int>())).Throws(MakeSqlException()); var sut = new SomeController(td.Object); var actual = sut.GetUser(1234); Assert.NotNull(actual); }
It's just an example, but the point is that since you can make a dynamic mock do anything that you can define in code, you can also use it to simulate database exceptions. This test pretends that the IUserRepository throws a SqlException from the Create method.
Perhaps the GetUser implementation now looks like this:
public User GetUser(int userId) { var u = this.userRepository.Read(userId); if (u.Id == 0) try { this.userRepository.Create(userId); } catch (SqlException) { } return u; }
If you find the example contrived, I don't blame you. The IUserRepository interface, the User class, and the GetUser method that orchestrates them are all degenerate in various ways. I originally created this little code example to discuss data flow verification, and I'm now stretching it beyond any reason. I hope that you can look past that. The point I'm making here is more general, and doesn't hinge on particulars.
Fake #
The article also suggests a FakeUserRepository that is small enough that I can repeat it here.
public sealed class FakeUserRepository : Collection<User>, IUserRepository { public void Create(int userId) { Add(new User { Id = userId }); } public User Read(int userId) { var user = this.SingleOrDefault(u => u.Id == userId); if (user == null) return new User { Id = 0 }; return user; } }
The question is how to use something like this when you want to test exceptions? It's possible that this little class may produce errors that I've failed to predict, but it certainly doesn't throw any SqlExceptions!
Should we inflate FakeUserRepository by somehow also giving it the capability to throw particular exceptions?
Throwing exceptions from Test Doubles #
I understand why AmirB asks that question, because it doesn't seem right. As a start, it would go against the Single Responsibility Principle. The FakeUserRepository would then have more than reason to change: You'd have to change it if the IUserRepository interface changes, but you'd also have to change it if you wanted to simulate a different error situation.
Good coding practices apply to test code as well. Test code is code that you have to read and maintain, so all the good practices that keep production code in good shape also apply to test code. This may include the SOLID principles, unless you're of the mind that SOLID ought to be a thing of the past.
If you really must throw exceptions from a Test Double, perhaps a dynamic mock object as shown above is the best option. No-one says that if you use a Fake Object for most of your tests you can't use a dynamic mock library for truly one-off test cases.Or perhaps a one-off Test Double that throws the desired exception.
I would, however, consider it a code smell if this happens too often. Not a test smell, but a code smell.
Is the exception part of the contract? #
You may ask yourself whether a particular exception type is part of an object's contract. As I always do, when I use the word contract, I refer to a set of invariants, pre-, and postconditions, taking a cue from Object-Oriented Software Construction. See also my video course Encapsulation and SOLID for more details.
You can imply many things about a contract when you have a static type system at your disposal, but there are always rules that you can't express that way. Parts of a contract are implicitly understood, or communicated in other ways. Code comments, docstrings, or similar, are good options.
What may you infer from the IUserRepository interface? What should you not infer?
I'd expect the Read method to return a User object. This code example hails us from 2013, before C# had nullable reference types. Around that time I'd begun using Maybe to signal that the return value might be missing. This is a convention, so the reader needs to be aware of it in order to correctly infer that part of the contract. Since the Read method does not return Maybe<User> I might infer that a non-null User object is guaranteed; that's a post-condition.
These days, I'd also use asynchronous APIs to hint that I/O is involved, but again, the example is so old and simplified that this isn't the case here. Still, regardless of how this is communicated to the reader, if an interface (or base class) is intended for I/O, we may expect it to fail at times. In most languages, such errors manifest as exceptions.
At least two questions arise from such deliberations:
- Which exception types may the methods throw?
- Can you even handle such exceptions?
Should SqlException even be part of the contract? Isn't that an implementation detail?
The FakeUserRepository class neither uses SQL Server nor throws SqlExceptions. You may imagine other implementations that use a document database, or even just another relational database than SQL Server (Oracle, MySQL, PostgreSQL, etc.). Those wouldn't throw SqlExceptions, but perhaps other exception types.
According to the Dependency Inversion Principle,
"Abstractions should not depend upon details. Details should depend upon abstractions."
If we make SqlException part of the contract, an implementation detail becomes part of the contract. Not only that: With an implementation like the above GetUser method, which catches SqlException, we've also violated the Liskov Substitution Principle. If you injected another implementation, one that throws a different type of exception, the code would no longer work as intended.
Loosely coupled code shouldn't look like that.
Many specific exceptions are of a kind that you can't handle anyway. On the other hand, if you do decide to handle particular error scenarios, make it part of the contract, or, as Michael Feathers puts it, extend the domain.
Integration testing #
How should we unit test specific exception? Mu, we shouldn't.
"Personally, I avoid using try-catch blocks in repositories or controllers and prefer handling exceptions in middleware (e.g., ErrorHandler). In such cases, I write separate unit tests for the middleware. Could this be a more fitting approach?"
That is, I think, an excellent approach to those exceptions that that you've decided to not handle explicitly. Such middleware would typically log or otherwise notify operators that a problem has arisen. You could also write some general-purpose middleware that performs retries or implements the Circuit Breaker pattern, but reusable libraries that do that already exist. Consider using one.
Still, you may have decided to implement a particular feature by leveraging a capability of a particular piece of technology, and the code you intent to write is complicated enough, or important enough, that you'd like to have good test coverage. How do you do that?
I'd suggest an integration test.
I don't have a good example lying around that involves throwing specific exceptions, but something similar may be of service. The example code base that accompanies my book Code That Fits in Your Head pretends to be an online restaurant reservation system. Two concurrent clients may compete for the last table on a particular date; a typical race condition.
There are more than one way to address such a concern. As implied in a previous article, you may decide to rearchitect the entire application to be able to handle such edge cases in a robust manner. For the purposes of the book's example code base, however, I considered a lock-free architecture out of scope. Instead, I had in mind dealing with that issue by taking advantage of .NET and SQL Server's support for lightweight transactions via a TransactionScope. While this is a handy solution, it's utterly dependent on the technology stack. It's a good example of an implementation detail that I'd rather not expose to a unit test.
Instead, I wrote a self-hosted integration test that runs against a real SQL Server instance (automatically deployed and configured on demand). It tests behaviour rather than implementation details:
[Fact] public async Task NoOverbookingRace() { var start = DateTimeOffset.UtcNow; var timeOut = TimeSpan.FromSeconds(30); var i = 0; while (DateTimeOffset.UtcNow - start < timeOut) await PostTwoConcurrentLiminalReservations(start.DateTime.AddDays(++i)); } private static async Task PostTwoConcurrentLiminalReservations(DateTime date) { date = date.Date.AddHours(18.5); using var service = new RestaurantService(); var task1 = service.PostReservation(new ReservationDtoBuilder() .WithDate(date) .WithQuantity(10) .Build()); var task2 = service.PostReservation(new ReservationDtoBuilder() .WithDate(date) .WithQuantity(10) .Build()); var actual = await Task.WhenAll(task1, task2); Assert.Single(actual, msg => msg.IsSuccessStatusCode); Assert.Single( actual, msg => msg.StatusCode == HttpStatusCode.InternalServerError); }
This test attempts to make two concurrent reservations for ten people. This is also the maximum capacity of the restaurant: It's impossible to seat twenty people. We'd like for one of the requests to win that race, while the server should reject the loser.
This test is only concerned with the behaviour that clients can observe, and since this code base contains hundreds of other tests that inspect HTTP response messages, this one only looks at the status codes.
The implementation handles the potential overbooking scenario like this:
private async Task<ActionResult> TryCreate(Restaurant restaurant, Reservation reservation) { using var scope = new TransactionScope(TransactionScopeAsyncFlowOption.Enabled); var reservations = await Repository.ReadReservations(restaurant.Id, reservation.At); var now = Clock.GetCurrentDateTime(); if (!restaurant.MaitreD.WillAccept(now, reservations, reservation)) return NoTables500InternalServerError(); await Repository.Create(restaurant.Id, reservation); scope.Complete(); return Reservation201Created(restaurant.Id, reservation); }
Notice the TransactionScope.
I'm under the illusion that I could radically change this implementation detail without breaking the above test. Granted, unlike another experiment, this hypothesis isn't one I've put to the test.
Conclusion #
How does one automatically test error branches? Most unit testing frameworks come with APIs that makes it easy to verify that specific exceptions were thrown, so that's not the hard part. If a particular exception is part of the System Under Test's contract, just test it like that.
On the other hand, when it comes to objects composed with other objects, implementation details may easily leak through in the shape of specific exception types. I'd think twice before writing a test that verifies whether a piece of client code (such as the above SomeController) handles a particular exception type (such as SqlException).
If such a test is difficult to write because all you have is a Fake Object (e.g. FakeUserRepository), that's only good. The rapid feedback furnished by test-driven development strikes again. Listen to your tests.
You should probably not write that test at all, because there seems to be an issue with the planned structure of the code. Address that problem instead.
Extracting data from a small CSV file with Haskell
Statically typed languages are also good for ad-hoc scripting.
This article is part of a short series of articles that compares ad-hoc scripting in Haskell with solving the same problem in Python. The introductory article describes the problem to be solved, so here I'll jump straight into the Haskell code. In the next article I'll give a similar walkthrough of my Python script.
Getting started #
When working with Haskell for more than a few true one-off expressions that I can type into GHCi (the Haskell REPL), I usually create a module file. Since I'd been asked to crunch some data, and I wasn't feeling very imaginative that day, I just named the module (and the file) Crunch. After some iterative exploration of the problem, I also arrived at a set of imports:
module Crunch where import Data.List (sort) import qualified Data.List.NonEmpty as NE import Data.List.Split import Control.Applicative import Control.Monad import Data.Foldable
As we go along, you'll see where some of these fit in.
Reading the actual data file, however, can be done with just the Haskell Prelude:
inputLines = words <$> readFile "survey_data.csv"
Already now, it's possible to load the module in GHCi and start examining the data:
ghci> :l Crunch.hs [1 of 1] Compiling Crunch ( Crunch.hs, interpreted ) Ok, one module loaded. ghci> length <$> inputLines 38
Looks good, but reading a text file is hardly the difficult part. The first obstacle, surprisingly, is to split comma-separated values into individual parts. For some reason that I've never understood, the Haskell base library doesn't even include something as basic as String.Split from .NET. I could probably hack together a function that does that, but on the other hand, it's available in the split package; that explains the Data.List.Split import. It's just a bit of a bother that one has to pull in another package only to do that.
Grades #
Extracting all the grades are now relatively easy. This function extracts and parses a grade from a single line:
grade :: Read a => String -> a grade line = read $ splitOn "," line !! 2
It splits the line on commas, picks the third element (zero-indexed, of course, so element 2), and finally parses it.
One may experiment with it in GHCi to get an impression that it works:
ghci> fmap grade <$> inputLines :: IO [Int] [2,2,12,10,4,12,2,7,2,2,2,7,2,7,2,4,2,7,4,7,0,4,0,7,2,2,2,2,2,2,4,4,2,7,4,0,7,2]
This lists all 38 expected grades found in the data file.
In the introduction article I spent some time explaining how languages with strong type inference don't need type declarations. This makes iterative development easier, because you can fiddle with an expression until it does what you'd like it to do. When you change an expression, often the inferred type changes as well, but there's no programmer overhead involved with that. The compiler figures that out for you.
Even so, the above grade function does have a type annotation. How does that gel with what I just wrote?
It doesn't, on the surface, but when I was fiddling with the code, there was no type annotation. The Haskell compiler is perfectly happy to infer the type of an expression like
grade line = read $ splitOn "," line !! 2
The human reader, however, is not so clever (I'm not, at least), so once a particular expression settles, and I'm fairly sure that it's not going to change further, I sometimes add the type annotation to aid myself.
When writing this, I was debating the didactics of showing the function with the type annotation, against showing it without it. Eventually I decided to include it, because it's more understandable that way. That decision, however, prompted this explanation.
Binomial choice #
The next thing I needed to do was to list all pairs from the data file. Usually, when I run into a problem related to combinations, I reach for applicative composition. For example, to list all possible combinations of the first three primes, I might do this:
ghci> liftA2 (,) [2,3,5] [2,3,5] [(2,2),(2,3),(2,5),(3,2),(3,3),(3,5),(5,2),(5,3),(5,5)]
You may now protest that this is sampling with replacement, whereas the task is to pick two different rows from the data file. Usually, when I run into that requirement, I just remove the ones that pick the same value twice:
ghci> filter (uncurry (/=)) $ liftA2 (,) [2,3,5] [2,3,5] [(2,3),(2,5),(3,2),(3,5),(5,2),(5,3)]
That works great as long as the values are unique, but what if that's not the case?
ghci> liftA2 (,) "foo" "foo"
[('f','f'),('f','o'),('f','o'),('o','f'),('o','o'),('o','o'),('o','f'),('o','o'),('o','o')]
ghci> filter (uncurry (/=)) $ liftA2 (,) "foo" "foo"
[('f','o'),('f','o'),('o','f'),('o','f')]
This removes too many values! We don't want the combinations where the first o is paired with itself, or when the second o is paired with itself, but we do want the combination where the first o is paired with the second, and vice versa.
This is relevant because the data set turns out to contain identical rows. Thus, I needed something that would deal with that issue.
Now, bear with me, because it's quite possible that what i did do isn't the simplest solution to the problem. On the other hand, I'm reporting what I did, and how I used Haskell to solve a one-off problem. If you have a simpler solution, please leave a comment.
You often reach for the tool that you already know, so I used a variation of the above. Instead of combining values, I decided to combine row indices instead. This meant that I needed a function that would produce the indices for a particular list:
indices :: Foldable t => t a -> [Int] indices f = [0 .. length f - 1]
Again, the type annotation came later. This just produces sequential numbers, starting from zero:
ghci> indices <$> inputLines [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20, 21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]
Such a function hovers just around the Fairbairn threshold; some experienced Haskellers would probably just inline it.
Since row numbers (indices) are unique, the above approach to binomial choice works, so I also added a function for that:
choices :: Eq a => [a] -> [(a, a)] choices = filter (uncurry (/=)) . join (liftA2 (,))
Combined with indices I can now enumerate all combinations of two rows in the data set:
ghci> choices . indices <$> inputLines [(0,1),(0,2),(0,3),(0,4),(0,5),(0,6),(0,7),(0,8),(0,9),...
I'm only showing the first ten results here, because in reality, there are 1406 such pairs.
Perhaps you think that all of this seems quite elaborate, but so far it's only four lines of code. The reason it looks like more is because I've gone to some lengths to explain what the code does.
Sum of grades #
The above combinations are pairs of indices, not values. What I need is to use each index to look up the row, from the row get the grade, and then sum the two grades. The first parts of that I can accomplish with the grade function, but I need to do if for every row, and for both elements of each pair.
While tuples are Functor instances, they only map over the second element, and that's not what I need:
ghci> rows = ["foo", "bar", "baz"] ghci> fmap (rows!!) <$> [(0,1),(0,2)] [(0,"bar"),(0,"baz")]
While this is just a simple example that maps over the two pairs (0,1) and (0,2), it illustrates the problem: It only finds the row for each tuple's second element, but I need it for both.
On the other hand, a type like (a, a) gives rise to a functor, and while a wrapper type like that is not readily available in the base library, defining one is a one-liner:
newtype Pair a = Pair { unPair :: (a, a) } deriving (Eq, Show, Functor)
This enables me to map over pairs in one go:
ghci> unPair <$> fmap (rows!!) <$> Pair <$> [(0,1),(0,2)]
[("foo","bar"),("foo","baz")]
This makes things a little easier. What remains is to use the grade function to look up the grade value for each row, then add the two numbers together, and finally count how many occurrences there are of each:
sumGrades ls = liftA2 (,) NE.head length <$> NE.group (sort (uncurry (+) . unPair . fmap (grade . (ls !!)) . Pair <$> choices (indices ls)))
You'll notice that this function doesn't have a type annotation, but we can ask GHCi if we're curious:
ghci> :t sumGrades sumGrades :: (Ord a, Num a, Read a) => [String] -> [(a, Int)]
This enabled me to get a count of each sum of grades:
ghci> sumGrades <$> inputLines [(0,6),(2,102),(4,314),(6,238),(7,48),(8,42),(9,272),(10,6), (11,112),(12,46),(14,138),(16,28),(17,16),(19,32),(22,4),(24,2)]
The way to read this is that the sum 0 occurs six times, 2 appears 102 times, etc.
There's one remaining task to accomplish before we can produce a PMF of the sum of grades: We need to enumerate the range, because, as it turns out, there are sums that are possible, but that don't appear in the data set. Can you spot which ones?
Using tools already covered, it's easy to enumerate all possible sums:
ghci> import Data.List ghci> sort $ nub $ (uncurry (+)) <$> join (liftA2 (,)) [-3,0,2,4,7,10,12] [-6,-3,-1,0,1,2,4,6,7,8,9,10,11,12,14,16,17,19,20,22,24]
The sums -6, -3, -1, and more, are possible, but don't appear in the data set. Thus, in the PMF for two randomly picked grades, the probability that the sum is -6 is 0. On the other hand, the probability that the sum is 0 is 6/1406 ~ 0.004267, and so on.
Difference of experience levels #
The other question posed in the assignment was to produce the PMF for the absolute difference between two randomly selected students' experience levels.
Answering that question follows the same mould as above. First, extract experience level from each data row, instead of the grade:
experience :: Read a => String -> a experience line = read $ splitOn "," line !! 3
Since I was doing an ad-hoc script, I just copied the grade function and changed the index from 2 to 3. Enumerating the experience differences were also a close copy of sumGrades:
diffExp ls = liftA2 (,) NE.head length <$> NE.group (sort (abs . uncurry (-) . unPair . fmap (experience . (ls !!)) . Pair <$> choices (indices ls)))
Running it in the REPL produces some other numbers, to be interpreted the same way as above:
ghci> diffExp <$> inputLines [(0,246),(1,472),(2,352),(3,224),(4,82),(5,24),(6,6)]
This means that the difference 0 occurs 246 times, 1 appears 472 times, and so on. From those numbers, it's fairly simple to set up the PMF.
Figures #
Another part of the assignment was to produce plots of both PMFs. I don't know how to produce figures with Haskell, and since the final results are just a handful of numbers each, I just copied them into a text editor to align them, and then pasted them into Excel to produce the figures there.
Here's the PMF for the differences:
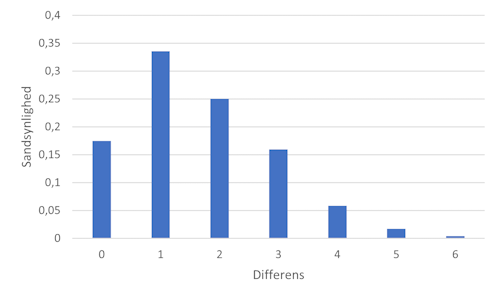
I originally created the figure with Danish labels. I'm sure that you can guess what differens means, and sandsynlighed means probability.
Conclusion #
In this article you've seen the artefacts of an ad-hoc script to extract and analyze a small data set. While I've spent quite a few words to explain what's going on, the entire Crunch module is only 34 lines of code. Add to that a few ephemeral queries done directly in GHCi, but never saved to a file. It's been some months since I wrote the code, but as far as I recall, it took me a few hours all in all.
If you do stuff like this every day, you probably find that appalling, but data crunching isn't really my main thing.
Is it quicker to do it in Python? Not for me, it turns out. It also took me a couple of hours to repeat the exercise in Python.
Range as a functor
With examples in C#, F#, and Haskell.
This article is an instalment in a short series of articles on the Range kata. In the previous three articles you've seen the Range kata implemented in Haskell, in F#, and in C#.
The reason I engaged with this kata was that I find that it provides a credible example of a how a pair of functors itself forms a functor. In this article, you'll see how that works out in three languages. If you don't care about one or two of those languages, just skip that section.
Haskell perspective #
If you've done any Haskell programming, you may be thinking that I have in mind the default Functor instances for tuples. As part of the base library, tuples (pairs, triples, quadruples, etc.) are already Functor instances. Specifically for pairs, we have this instance:
instance Functor ((,) a)
Those are not the functor instances I have in mind. To a degree, I find these default Functor instances unfortunate, or at least arbitrary. Let's briefly explore the above instance to see why that is.
Haskell is a notoriously terse language, but if we expand the above instance to (invalid) pseudocode, it says something like this:
instance Functor ((a,b) b)
What I'm trying to get across here is that the a type argument is fixed, and only the second type argument b can be mapped. Thus, you can map a (Bool, String) pair to a (Bool, Int) pair:
ghci> fmap length (True, "foo") (True,3)
but the first element (Bool, in this example) is fixed, and you can't map that. To be clear, the first element can be any type, but once you've fixed it, you can't change it (within the constraints of the Functor API, mind):
ghci> fmap (replicate 3) (42, 'f')
(42,"fff")
ghci> fmap ($ 3) ("bar", (* 2))
("bar",6)
The reason I find these default instances arbitrary is that this isn't the only possible Functor instance. Pairs, in particular, are also Bifunctor instances, so you can easily map over the first element, instead of the second:
ghci> first show (42, 'f')
("42",'f')
Similarly, one can easily imagine a Functor instance for triples (three-tuples) that map the middle element. The default instance, however, maps the third (i.e. last) element only.
There are some hand-wavy rationalizations out there that argue that in Haskell, application and reduction is usually done from the right, so therefore it's most appropriate to map over the rightmost element of tuples. I admit that it at least argues from a position of consistency, and it does make it easier to remember, but from a didactic perspective I still find it a bit unfortunate. It suggests that a tuple functor only maps the last element.
What I had in mind for ranges however, wasn't to map only the first or the last element. Neither did I wish to treat ranges as bifunctors. What I really wanted was the ability to project an entire range.
In my Haskell Range implementation, I'd simply treated ranges as tuples of Endpoint values, and although I didn't show that in the article, I ultimately declared Endpoint as a Functor instance:
data Endpoint a = Open a | Closed a deriving (Eq, Show, Functor)
This enables you to map a single Endpoint value:
ghci> fmap length $ Closed "foo" Closed 3
That's just a single value, but the Range kata API operates with pairs of Endpoint value. For example, the contains function has this type:
contains :: (Foldable t, Ord a) => (Endpoint a, Endpoint a) -> t a -> Bool
Notice the (Endpoint a, Endpoint a) input type.
Is it possible to treat such a pair as a functor? Yes, indeed, just import Data.Functor.Product, which enables you to package two functor values in a single wrapper:
ghci> import Data.Functor.Product ghci> Pair (Closed "foo") (Open "corge") Pair (Closed "foo") (Open "corge")
Now, granted, the Pair data constructor doesn't wrap a tuple, but that's easily fixed:
ghci> uncurry Pair (Closed "foo", Open "corge") Pair (Closed "foo") (Open "corge")
The resulting Pair value is a Functor instance, which means that you can project it:
ghci> fmap length $ uncurry Pair (Closed "foo", Open "corge") Pair (Closed 3) (Open 5)
Now, granted, I find the Data.Functor.Product API a bit lacking in convenience. For instance, there's no getPair function to retrieve the underlying values; you'd have to use pattern matching for that.
In any case, my motivation for covering this ground wasn't to argue that Data.Functor.Product is all we need. The point was rather to observe that when you have two functors, you can combine them, and the combination is also a functor.
This is one of the many reasons I get so much value out of Haskell. Its abstraction level is so high that it substantiates relationships that may also exist in other code bases, written in other programming languages. Even if a language like F# or C# can't formally express some of those abstraction, you can still make use of them as 'design patterns' (for lack of a better term).
F# functor #
What we've learned from Haskell is that if we have two functors we can combine them into one. Specifically, I made Endpoint a Functor instance, and from that followed automatically that a Pair of those was also a Functor instance.
I can do the same in F#, starting with Endpoint. In F# I've unsurprisingly defined the type like this:
type Endpoint<'a> = Open of 'a | Closed of 'a
That's just a standard discriminated union. In order to make it a functor, you'll have to add a map function:
module Endpoint = let map f = function | Open x -> Open (f x) | Closed x -> Closed (f x)
The function alone, however, isn't enough to give rise to a functor. We must also convince ourselves that the map function obeys the functor laws. One way to do that is to write tests. While tests aren't proofs, we may still be sufficiently reassured by the tests that that's good enough for us. While I could, I'm not going to prove that Endpoint.map satisfies the functor laws. I will, later, do just that with the pair, but I'll leave this one as an exercise for the interested reader.
Since I was already using Hedgehog for property-based testing in my F# code, it was obvious to write properties for the functor laws as well.
[<Fact>] let ``First functor law`` () = Property.check <| property { let genInt32 = Gen.int32 (Range.linearBounded ()) let! expected = Gen.choice [Gen.map Open genInt32; Gen.map Closed genInt32] let actual = Endpoint.map id expected expected =! actual }
This property exercises the first functor law for integer endpoints. Recall that this law states that if you map a value with the identity function, nothing really happens.
The second functor law is more interesting.
[<Fact>] let ``Second functor law`` () = Property.check <| property { let genInt32 = Gen.int32 (Range.linearBounded ()) let! endpoint = Gen.choice [Gen.map Open genInt32; Gen.map Closed genInt32] let! f = Gen.item [id; ((+) 1); ((*) 2)] let! g = Gen.item [id; ((+) 1); ((*) 2)] let actual = Endpoint.map (f << g) endpoint Endpoint.map f (Endpoint.map g endpoint) =! actual }
This property again exercises the property for integer endpoints. Not only does the property pick a random integer and varies whether the Endpoint is Open or Closed, it also picks two random functions from a small list of functions: The identity function (again), a function that increments by one, and a function that doubles the input. These two functions, f and g, might then be the same, but might also be different from each other. Thus, the composition f << g might be id << id or ((+) 1) << ((+) 1), but might just as well be ((+) 1) << ((*) 2), or one of the other possible combinations.
The law states that the result should be the same regardless of whether you first compose the functions and then map them, or map them one after the other.
Which is the case.
A Range is defined like this:
type Range<'a> = { LowerBound : Endpoint<'a>; UpperBound : Endpoint<'a> }
This record type also gives rise to a functor:
module Range = let map f { LowerBound = lowerBound; UpperBound = upperBound } = { LowerBound = Endpoint.map f lowerBound UpperBound = Endpoint.map f upperBound }
This map function uses the projection f on both the lowerBound and the upperBound. It, too, obeys the functor laws:
[<Fact>] let ``First functor law`` () = Property.check <| property { let genInt64 = Gen.int64 (Range.linearBounded ()) let genEndpoint = Gen.choice [Gen.map Open genInt64; Gen.map Closed genInt64] let! expected = Gen.tuple genEndpoint |> Gen.map Range.ofEndpoints let actual = expected |> Ploeh.Katas.Range.map id expected =! actual } [<Fact>] let ``Second functor law`` () = Property.check <| property { let genInt16 = Gen.int16 (Range.linearBounded ()) let genEndpoint = Gen.choice [Gen.map Open genInt16; Gen.map Closed genInt16] let! range = Gen.tuple genEndpoint |> Gen.map Range.ofEndpoints let! f = Gen.item [id; ((+) 1s); ((*) 2s)] let! g = Gen.item [id; ((+) 1s); ((*) 2s)] let actual = range |> Ploeh.Katas.Range.map (f << g) Ploeh.Katas.Range.map f (Ploeh.Katas.Range.map g range) =! actual }
These two Hedgehog properties are cast in the same mould as the Endpoint properties, only they create 64-bit and 16-bit ranges for variation's sake.
C# functor #
As I wrote about the Haskell result, it teaches us which abstractions are possible, even if we can't formalise them to the same degree in, say, C# as we can in Haskell. It should come as no surprise, then, that we can also make Range<T> a functor in C#.
In C# we idiomatically do that by giving a class a Select method. Again, we'll have to begin with Endpoint:
public Endpoint<TResult> Select<TResult>(Func<T, TResult> selector) { return Match( whenClosed: x => Endpoint.Closed(selector(x)), whenOpen: x => Endpoint.Open(selector(x))); }
Does that Select method obey the functor laws? Yes, as we can demonstrate (not prove) with a few properties:
[Fact] public void FirstFunctorLaw() { Gen.OneOf( Gen.Int.Select(Endpoint.Open), Gen.Int.Select(Endpoint.Closed)) .Sample(expected => { var actual = expected.Select(x => x); Assert.Equal(expected, actual); }); } [Fact] public void ScondFunctorLaw() { (from endpoint in Gen.OneOf( Gen.Int.Select(Endpoint.Open), Gen.Int.Select(Endpoint.Closed)) from f in Gen.OneOfConst<Func<int, int>>(x => x, x => x + 1, x => x * 2) from g in Gen.OneOfConst<Func<int, int>>(x => x, x => x + 1, x => x * 2) select (endpoint, f, g)) .Sample(t => { var actual = t.endpoint.Select(x => t.g(t.f(x))); Assert.Equal( t.endpoint.Select(t.f).Select(t.g), actual); }); }
These two tests follow the scheme laid out by the above F# properties, and they both pass.
The Range class gets the same treatment. First, a Select method:
public Range<TResult> Select<TResult>(Func<T, TResult> selector) where TResult : IComparable<TResult> { return new Range<TResult>(min.Select(selector), max.Select(selector)); }
which, again, can be demonstrated with two properties that exercise the functor laws:
[Fact] public void FirstFunctorLaw() { var genEndpoint = Gen.OneOf( Gen.Int.Select(Endpoint.Closed), Gen.Int.Select(Endpoint.Open)); genEndpoint.SelectMany(min => genEndpoint .Select(max => new Range<int>(min, max))) .Sample(sut => { var actual = sut.Select(x => x); Assert.Equal(sut, actual); }); } [Fact] public void SecondFunctorLaw() { var genEndpoint = Gen.OneOf( Gen.Int.Select(Endpoint.Closed), Gen.Int.Select(Endpoint.Open)); (from min in genEndpoint from max in genEndpoint from f in Gen.OneOfConst<Func<int, int>>(x => x, x => x + 1, x => x * 2) from g in Gen.OneOfConst<Func<int, int>>(x => x, x => x + 1, x => x * 2) select (sut : new Range<int>(min, max), f, g)) .Sample(t => { var actual = t.sut.Select(x => t.g(t.f(x))); Assert.Equal( t.sut.Select(t.f).Select(t.g), actual); }); }
These tests also pass.
Laws #
Exercising a pair of properties can give us a good warm feeling that the data structures and functions defined above are proper functors. Sometimes, tests are all we have, but in this case we can do better. We can prove that the functor laws always hold.
The various above incarnations of a Range type are all product types, and the canonical form of a product type is a tuple (see e.g. Thinking with Types for a clear explanation of why that is). That's the reason I stuck with a tuple in my Haskell code.
Consider the implementation of the fmap implementation of Pair:
fmap f (Pair x y) = Pair (fmap f x) (fmap f y)
We can use equational reasoning, and as always I'll use the the notation that Bartosz Milewski uses. It's only natural to begin with the first functor law, using F and G as placeholders for two arbitrary Functor data constructors.
fmap id (Pair (F x) (G y))
= { definition of fmap }
Pair (fmap id (F x)) (fmap id (G y))
= { first functor law }
Pair (F x) (G y)
= { definition of id }
id (Pair (F x) (G y))
Keep in mind that in this notation, the equal signs are true equalities, going both ways. Thus, you can read this proof from the top to the bottom, or from the bottom to the top. The equality holds both ways, as should be the case for a true equality.
We can proceed in the same vein to prove the second functor law, being careful to distinguish between Functor instances (F and G) and functions (f and g):
fmap (g . f) (Pair (F x) (G y))
= { definition of fmap }
Pair (fmap (g . f) (F x)) (fmap (g . f) (G y))
= { second functor law }
Pair ((fmap g . fmap f) (F x)) ((fmap g . fmap f) (G y))
= { definition of composition }
Pair (fmap g (fmap f (F x))) (fmap g (fmap f (G y)))
= { definition of fmap }
fmap g (Pair (fmap f (F x)) (fmap f (G y)))
= { definition of fmap }
fmap g (fmap f (Pair (F x) (G y)))
= { definition of composition }
(fmap g . fmap f) (Pair (F x) (G y))
Notice that both proofs make use of the functor laws. This may seem self-referential, but is rather recursive. When the proofs refer to the functor laws, they refer to the functors F and G, which are both assumed to be lawful.
This is how we know that the product of two lawful functors is itself a functor.
Negations #
During all of this, you may have thought: What happens if we project a range with a negation?
As a simple example, let's consider the range from -1 to 2:
ghci> uncurry Pair (Closed (-1), Closed 2) Pair (Closed (-1)) (Closed 2)
We may draw this range on the number line like this:

What happens if we map that range by multiplying with -1?
ghci> fmap negate $ uncurry Pair (Closed (-1), Closed 2) Pair (Closed 1) (Closed (-2))
We get a range from 1 to -2!
Aha! you say, clearly that's wrong! We've just found a counterexample. After all, range isn't a functor.
Not so. The functor laws say nothing about the interpretation of projections (but I'll get back to that in a moment). Rather, they say something about composition, so let's consider an example that reaches a similar, seemingly wrong result:
ghci> fmap ((+1) . negate) $ uncurry Pair (Closed (-1), Closed 2) Pair (Closed 2) (Closed (-1))
This is a range from 2 to -1, so just as problematic as before.
The second functor law states that the outcome should be the same if we map piecewise:
ghci> (fmap (+ 1) . fmap negate) $ uncurry Pair (Closed (-1), Closed 2) Pair (Closed 2) (Closed (-1))
Still a range from 2 to -1. The second functor law holds.
But, you protest, that's doesn't make any sense!
I disagree. It could make sense in at least three different ways.
What does a range from 2 to -1 mean? I can think of three interpretations:
- It's the empty set
- It's the range from -1 to 2
- It's the set of numbers that are either less than or equal to -1 or greater than or equal to 2
We may illustrate those three interpretations, together with the original range, like this:
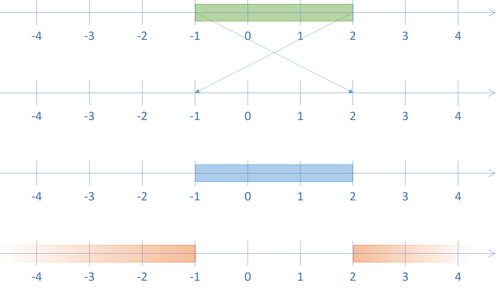
According to the first interpretation, we consider the range as the Boolean and of two predicates. In this interpretation the initial range is really the Boolean expression -1 ≤ x ∧ x ≤ 2. The projected range then becomes the expression 2 ≤ x ∧ x ≤ -1, which is not possible. This is how I've chosen to implement the contains function:
ghci> Pair x y = fmap ((+1) . negate) $ uncurry Pair (Closed (-1), Closed 2) ghci> contains (x, y) [0] False ghci> contains (x, y) [-3] False ghci> contains (x, y) [4] False
In this interpretation, the result is the empty set. The range isn't impossible; it's just empty. That's the second number line from the top in the above illustration.
This isn't, however, the only interpretation. Instead, we may choose to be liberal in what we accept and interpret the range from 2 to -1 as a 'programmer mistake': What you asked me to do is formally wrong, but I think that I understand that you meant the range from -1 to 2.
That's the third number line in the above illustration.
The fourth interpretation is that when the first element of the range is greater than the second, the range represents the complement of the range. That's the fourth number line in the above illustration.
The reason I spent some time on this is that it's easy to confuse the functor laws with other properties that you may associate with a data structure. This may lead you to falsely conclude that a functor isn't a functor, because you feel that it violates some other invariant.
If this happens, consider instead whether you could possibly expand the interpretation of the data structure in question.
Conclusion #
You can model a range as a functor, which enables you to project ranges, either moving them around on an imaginary number line, or changing the type of the range. This might for example enable you to map a date range to an integer range, or vice versa.
A functor enables mapping or projection, and some maps may produce results that you find odd or counter-intuitive. In this article you saw an example of that in the shape of a negated range where the first element (the 'minimum', in one interpretation) becomes greater than the second element (the 'maximum'). You may take that as an indication that the functor isn't, after all, a functor.
This isn't the case. A data structure and its map function is a functor if the the mapping obeys the functor laws, which is the case for the range structures you've seen here.
Statically and dynamically typed scripts
Extracting and analysing data in Haskell and Python.
I was recently following a course in mathematical analysis and probability for computer scientists. One assignment asked to analyze a small CSV file with data collected in a student survey. The course contained a mix of pure maths and practical application, and the official programming language to be used was Python. It was understood that one was to do the work in Python, but it wasn't an explicit requirement, and I was so tired that didn't have the energy for it.
I can get by in Python, but it's not a language I'm actually comfortable with. For small experiments, ad-hoc scripting, etc. I reach for Haskell, so that's what I did.
This was a few months ago, and I've since followed another course that required more intense use of Python. With a few more months of Python programming under my belt, I decided to revisit that old problem and do it in Python with the explicit purpose of comparing and contrasting the two.
Static or dynamic types for scripting #
I'd like to make one point with these articles, and that is that dynamically typed languages aren't inherently better suited for scripting than statically typed languages. From this, it does not, however, follow that statically typed languages are better, either. Rather, I increasingly believe that whether you find one or the other more productive is a question of personality, past experiences, programming background, etc. I've been over this ground before. Many of my heroes seem to favour dynamically typed languages, while I keep returning to statically typed languages.
For more than a decade I've preferred F# or Haskell for ad-hoc scripting. Note that while these languages are statically typed, they are low on ceremony. Types are inferred rather than declared. This means that for scripts, you can experiment with small code blocks, iteratively move closer to what you need, just as you would with a language like Python. Change a line of code, and the inferred type changes with it; there are no type declarations that you also need to fix.
When I talk about writing scripts in statically typed languages, I have such languages in mind. I wouldn't write a script in C#, C, or Java.
"Let me stop you right there: I don't think there is a real dynamic typing versus static typing debate.
"What such debates normally are is language X vs language Y debates (where X happens to be dynamic and Y happens to be static)."
The present articles compare Haskell and Python, so be careful that you don't extrapolate and draw any conclusions about, say, C++ versus Erlang.
When writing an ad-hoc script to extract data from a file, it's important to be able to experiment and iterate. Load the file, inspect the data, figure out how to extract subsets of it (particular columns, for example), calculate totals, averages, etc. A REPL is indispensable in such situations. The Haskell REPL (called Glasgow Haskell Compiler interactive, or just GHCi) is the best one I've encountered.
I imagine that a Python expert would start by reading the data to slice and dice it various ways. We may label this a data-first approach, but be careful not to read too much into this, as I don't really know what I'm talking about. That's not how my mind works. Instead, I tend to take a types-first approach. I'll look at the data and start with the types.
The assignment #
The actual task is the following. At the beginning of the course, the professors asked students to fill out a survey. Among the questions asked was which grade the student expected to receive, and how much experience with programming he or she already had.
Grades are given according to the Danish academic scale: -3, 00, 02, 4, 7, 10, and 12, and experience level on a simple numeric scale from 1 to 7, with 1 indicating no experience and 7 indicating expert-level experience.
Here's a small sample of the data:
No,3,2,6,6 No,4,2,3,7 No,1,12,6,2 No,4,10,4,3 No,3,4,4,6
The expected grade is in the third column (i.e. 2, 2, 12, 10, 4) and the experience level is in the fourth column (6,3,6,4,4). The other columns are answers to different survey questions. The full data set contains 38 rows.
The assignment poses the following questions: Two rows from the survey data are randomly selected. What is the probability mass function (PMF) of the sum of their expected grades, and what is the PMF of the absolute difference between their programming experience levels?
In both cases I was also asked to plot the PMFs.
Comparisons #
As outlined above, I originally wrote a Haskell script to answer the questions, and only months later returned to the problem to give it a go in Python. When reading my detailed walkthroughs, keep in mind that I have 8-9 years of Haskell experience, and that I tend to 'think in Haskell', while I have only about a year of experience with Python. I don't consider myself proficient with Python, so the competition is rigged from the outset.
- Extracting data from a small CSV file with Haskell
- Extracting data from a small CSV file with Python
For this small task, I don't think that there's a clear winner. I still like my Haskell code the best, but I'm sure someone better at Python could write a much cleaner script. I also have to admit that Matplotlib makes it a breeze to produce nice-looking plots with Python, whereas I don't even know where to start with that with Haskell.
Recently I've done some more advanced data analysis with Python, such as random forest classification, principal component analysis, KNN-classification, etc. While I understand that I'm only scratching the surface of data science and machine learning, it's obvious that there's a rich Python ecosystem for that kind of work.
Conclusion #
This lays the foundations for comparing a small Haskell script with an equivalent Python script. There's no scientific method to the comparison; it's just me doing the same exercise twice, a bit like I'd do katas with multiple variations in order to learn.
While I still like Haskell better than Python, that's only a personal preference. I'm deliberately not declaring a winner.
One point I'd like to make, however, is that there's nothing inherently better about a dynamically typed language when it comes to ad-hoc scripting. Languages with strong type inference work well, too.
Error categories and category errors
How I currently think about errors in programming.
A reader recently asked a question that caused me to reflect on the way I think about errors in software. While my approach to error handling has remained largely the same for years, I don't think I've described it in an organized way. I'll try to present those thoughts here.
This article is, for lack of a better term, a think piece. I don't pretend that it represents any fundamental truth, or that this is the only way to tackle problems. Rather, I write this article for two reasons.
- Writing things down often helps clarifying your thoughts. While I already feel that my thinking on the topic of error handling is fairly clear, I've written enough articles that I know that by writing this one, I'll learn something new.
- Publishing this article enables the exchange of ideas. By sharing my thoughts, I enable readers to point out errors in my thinking, or to improve on my work. Again, I may learn something. Perhaps others will, too.
Although I don't claim that the following is universal, I've found it useful for years.
Error categories #
Almost all software is at risk of failing for a myriad of reasons: User input, malformed data, network partitions, cosmic rays, race conditions, bugs, etc. Even so, we may categorize errors like this:
- Predictable errors we can handle
- Predictable errors we can't handle
- Errors we've failed to predict
This distinction is hardly original. I believe I've picked it up from Michael Feathers, but although I've searched, I can't find the source, so perhaps I'm remembering it wrong.
You may find these three error categories underwhelming, but I find it useful to first consider what may be done about an error. Plenty of error situations are predictable. For example, all input should be considered suspect. This includes user input, but also data you receive from other systems. This kind of potential error you can typically solve with input validation, which I believe is a solved problem. Another predictable kind of error is unavailable services. Many systems store data in databases. You can easily predict that the database will, sooner or later, be unreachable. Potential causes include network partitions, a misconfigured connection string, logs running full, a crashed server, denial-of-service attacks, etc.
With some experience with software development, it's not that hard producing a list of things that could go wrong. The next step is to decide what to do about it.
There are scenarios that are so likely to happen, and where the solution is so well-known, that they fall into the category of predictable errors that you can handle. User input belongs here. You examine the input and inform the user if it's invalid.
Even with input, however, other scenarios may lead you down different paths. What if, instead of a system with a user interface, you're developing a batch job that receives a big data file every night? How do you deal with invalid input in that scenario? Do you reject the entire data set, or do you filter it so that you only handle the valid input? Do you raise a notification to asynchronously inform the sender that input was malformed?
Notice how categorization is context-dependent. It would be a (category?) error to interpret the above model as fixed and universal. Rather, it's an analysis framework that helps identifying how to categorize various fault scenarios in a particular application context.
Another example may be in order. If your system depends on a database, a predictable error is that the database will be unavailable. Can you handle that situation?
A common reaction is that there's really not a lot one can do about that. You may retry the operation, log the problem, or notify an on-call engineer, but ultimately the system depends on the database. If the database is unreachable, the system can't work. You can't handle that problem, so this falls in the category of predictable errors that you can't handle.
Or does it?
Trade-offs of error handling #
The example of an unreachable database is useful to explore in order to demonstrate that error handling isn't writ in stone, but rather an architectural design decision. Consider a common API design like this:
public interface IRepository<T> { int Create(T item); // other members }
What happens if client code calls Create but the database is unreachable? This is C# code, but the problem generalizes. With most implementations, the Create method will throw an exception.
Can you handle that situation? You may retry a couple of times, but if you have a user waiting for a response, you can't retry for too long. Once time is up, you'll have to accept that the operation failed. In a language like C#, the most robust implementation is to not handle the specific exception, but instead let it bubble up to be handled by a global exception handler that usually can't do much else than showing the user a generic error message, and then log the exception.
This isn't your only option, though. You may find yourself in a context where this kind of attitude towards errors is unacceptable. If you're working with BLOBAs it's probably fine, but if you're working with medical life-support systems, or deep-space probes, or in other high-value contexts, the overall error-tolerance may be lower. Then what do you do?
You may try to address the concern with IT operations: Configure failover systems for the database, installing two network cards in every machine, and so on. This may (also) be a way to address the problem, but isn't your only option. You may also consider changing the software architecture.
One option may be to switch to an asynchronous message-based system where messages are transmitted via durable queues. Granted, durables queues may fail as well (everything may fail), but when done right, they tend to be more robust. Even a machine that has lost all network connectivity may queue messages on its local disk until the network returns. Yes, the disk may run full, etc. but it's less likely to happen than a network partition or an unreachable database.
Notice that an unreachable database now goes into the category of errors that you've predicted, and that you can handle. On the other hand, failing to send an asynchronous message is now a new kind of error in your system: One that you can predict, but can't handle.
Making this change, however, impacts your software architecture. You can no longer have an interface method like the above Create method, because you can't rely on it returning an int in reasonable time. During error scenarios, messages may sit in queues for hours, if not days, so you can't block on such code.
As I've explained elsewhere you can instead model a Create method like this:
public interface IRepository<T> { void Create(Guid id, T item); // other members }
Not only does this follow the Command Query Separation principle, it also makes it easier for you to adopt an asynchronous message-based architecture. Done consistently, however, this requires that you approach application design in a way different from a design where you assume that the database is reachable.
It may even impact a user interface, because it'd be a good idea to design user experience in such a way that it helps the user have a congruent mental model of how the system works. This may include making the concept of an outbox explicit in the user interface, as it may help users realize that writes happen asynchronously. Most users understand that email works that way, so it's not inconceivable that they may be able to adopt a similar mental model of other applications.
The point is that this is an option that you may consider as an architect. Should you always design systems that way? I wouldn't. There's much extra complexity that you have to deal with in order to make asynchronous messaging work: UX, out-of-order messages, dead-letter queues, message versioning, etc. Getting to five nines is expensive, and often not warranted.
The point is rather that what goes in the predictable errors we can't handle category isn't fixed, but context-dependent. Perhaps we should rather name the category predictable errors we've decided not to handle.
Bugs #
How about the third category of errors, those we've failed to predict? We also call these bugs or defects. By definition, we only learn about them when they manifest. As soon as they become apparent, however, they fall into one of the other categories. If an error occurs once, it may occur again. It is now up to you to decide what to do about it.
I usually consider errors as stop-the-line-issues, so I'd be inclined to immediately address them. On they other hand, if you don't do that, you've implicitly decided to put them in the category of predictable errors that you've decided not to handle.
We don't intentionally write bugs; there will always be some of those around. On the other hand, various practices help reducing them: Test-driven development, code reviews, property-based testing, but also up-front design.
Error-free code #
Do consider explicitly how code may fail.
Despite the title of this section, there's no such thing as error-free code. Still, you can explicitly think about edge cases. For example, how might the following function fail?
public static TimeSpan Average(this IEnumerable<TimeSpan> timeSpans) { var sum = TimeSpan.Zero; var count = 0; foreach (var ts in timeSpans) { sum += ts; count++; } return sum / count; }
In at least two ways: The input collection may be empty or infinite. I've already suggested a few ways to address those problems. Some of them are similar to what Michael Feathers calls unconditional code, in that we may change the domain. Another option, that I didn't cover in the linked article, is to expand the codomain:
public static TimeSpan? Average(this IReadOnlyCollection<TimeSpan> timeSpans) { if (!timeSpans.Any()) return null; var sum = TimeSpan.Zero; foreach (var ts in timeSpans) sum += ts; return sum / timeSpans.Count; }
Now, instead of diminishing the domain, we expand the codomain by allowing the return value to be null. (Interestingly, this is the inverse of my profunctor description of the Liskov Substitution Principle. I don't yet know what to make of that. See: Just by writing things down, I learn something I hadn't realized before.)
This is beneficial in a statically typed language, because such a change makes hidden knowledge explicit. It makes it so explicit that a type checker can point out when we make mistakes. Make illegal states unrepresentable. Poka-yoke. A potential run-time exception is now a compile-time error, and it's firmly in the category of errors that we've predicted and decided to handle.
In the above example, we could use the built-in .NET Nullable<T> (with the ? syntactic-sugar alias). In other cases, you may resort to returning a Maybe (AKA option).
Modelling errors #
Explicitly expanding the codomain of functions to signal potential errors is beneficial if you expect the caller to be able to handle the problem. If callers can't handle an error, forcing them to deal with it is just going to make things more difficult. I've never done any professional Java programming, but I've heard plenty of Java developers complain about checked exceptions. As far as I can tell, the problem in Java isn't so much with the language feature per se, but rather with the exception types that APIs force you to handle.
As an example, imagine that every time you call a database API, the compiler forces you to handle an IOException. Unless you explicitly architect around it (as outlined above), this is likely to be one of the errors you can predict, but decide not to handle. But if the compiler forces you to handle it, then what do you do? You probably find some workaround that involves re-throwing the exception, or, as I understand that some Java developers do, declare that their own APIs may throw any exception, and by that means just pass the buck. Not helpful.
As far as I can tell, (checked) exceptions are equivalent to the Either container, also known as Result. We may imagine that instead of throwing exceptions, a function may return an Either value: Right for a right result (explicit mnemonic, there!), and left for an error.
It might be tempting to model all error-producing operations as Either-returning, but you're often better off using exceptions. Throw exceptions in those situations that you expect most clients can't recover from. Return left (or error) cases in those situations that you expect that a typical client would want to handle.
Again, it's context-specific, so if you're developing a reusable library, there's a balance to strike in API design (or overloads to supply).
Most errors are just branches #
In many languages, errors are somehow special. Most modern languages include a facility to model errors as exceptions, and special syntax to throw or catch them. (The odd man out may be C, with its reliance on error codes as return values, but that is incredible awkward for other reasons. You may also reasonably argue that C is hardly a modern language.)
Even Haskell has exceptions, even though it also has deep language support for Maybe and Either. Fortunately, Haskell APIs tend to only throw exceptions in those cases where average clients are unlikely to handle them: Timeouts, I/O failures, and so on.
It's unfortunate that languages treat errors as something exceptional, because this nudges us to make a proper category error: That errors are somehow special, and that we can't use normal coding constructs or API design practices to model them.
But you can. That's what Michael Feathers' presentation is about, and that's what you can do by making illegal states unrepresentable, or by returning Maybe or Either values.
Most errors are just branches in your code; where it diverges from the happy path in order to do something else.
Conclusion #
This article presents a framework for thinking about software errors. There are those you can predict may happen, and you choose to handle; those you predict may happen, but you choose to ignore; and those that you have not yet predicted: bugs.
A little up-front thinking will often help you predict some errors, but I'm not advocating that you foresee all errors. Some errors are programmer errors, and we make those errors because we're human, exactly because we're failing to predict the behaviour of a particular state of the code. Once you discover a bug, however, you have a choice: Do you address it or ignore it?
There are error conditions that you may deliberately choose to ignore. This doesn't necessarily make you an irresponsible programmer, but may rather be the result of a deliberate feasibility study. For example, every network operation may fail. How important is it that your application can keep running without the network? Is it worthwhile to make the code so robust that it can handle that situation? Or can you rather live with a few hours of downtime per quarter? If the latter, it may be best to let a human deal with network partitions when they occur.
The three error categories I suggest here are context-dependent. You decide which problems to deal with, and which ones to ignore, but apart from that, error-handling doesn't have to be difficult.
A Range kata implementation in C#
A port of the corresponding F# code.
This article is an instalment in a short series of articles on the Range kata. In the previous article I made a pass at the kata in F#, using property-based testing with Hedgehog to generate test data.
In the conclusion I mused about the properties I was able to come up with. Is it possible to describe open, closed, and mixed ranges in a way that's less coupled to the implementation? To be honest, I still don't have an answer to that question. Instead, in this article, I describe a straight port of the F# code to C#. There's value in that, too, for people who wonder how to reap the benefits of F# in C#.
The code is available on GitHub.
First property #
Both F# and C# are .NET languages. They run in the same substrate, and are interoperable. While Hedgehog is written in F#, it's possible to consume F# libraries from C#, and vice versa. I've done this multiple times with FsCheck, but I admit to never having tried it with Hedgehog.
If you want to try property-based testing in C#, a third alternative is available: CsCheck. It's written in C# and is more idiomatic in that context. While I sometimes still use FsCheck from C#, I often choose CsCheck for didactic reasons.
The first property I wrote was a direct port of the idea of the first property I wrote in F#:
[Fact] public void ClosedRangeContainsList() { (from xs in Gen.Short.Enumerable.Nonempty let min = xs.Min() let max = xs.Max() select (xs, min, max)) .Sample(t => { var sut = new Range<short>( new ClosedEndpoint<short>(t.min), new ClosedEndpoint<short>(t.max)); var actual = sut.Contains(t.xs); Assert.True(actual, $"Expected {t.xs} to be contained in {sut}."); }); }
This test (or property, if you will) uses a technique that I often use with property-based testing. I'm still searching for a catchy name for this, but here we may call it something like reverse test-case assembly. My goal is to test a predicate, and this particular property should verify that for a given Equivalence Class, the predicate is always true.
While we may think of an Equivalence Class as a set from which we pick test cases, I don't actually have a full enumeration of such a set. I can't have that, since that set is infinitely big. Instead of randomly picking values from a set that I can't fully populate, I instead carefully pick test case values in such a way that they would all belong to the same set partition (Equivalence Class).
The test name suggests the test case: I'd like to verify that given I have a closed range, when I ask it whether a list within that range is contained, then the answer is true. How do I pick such a test case?
I do it in reverse. You can say that the sampling is the dual of the test. I start with a list (xs) and only then do I create a range that contains it. Since the first test case is for a closed range, the min and max values are sufficient to define such a range.
How do I pass that property?
Degenerately, as is often the case with TDD beginnings:
public bool Contains(IEnumerable<T> candidates) { return true; }
Even though the ClosedRangeContainsList property effectively executes a hundred test cases, the Devil's Advocate can easily ignore that and instead return hard-coded true.
Endpoint sum type #
I'm not going to bore you with the remaining properties. The repository is available on GitHub if you're interested in those details.
If you've programmed in F# for some time, you typically miss algebraic data types when forced to return to C#. A language like C# does have product types, but lack native sum types. Even so, not all is lost. I've previously demonstrated that you can employ the Visitor pattern to encode a sum type. Another option is to use Church encoding, which I've decided to do here.
When choosing between Church encoding and the Visitor pattern, Visitor is more object-oriented (after all, it's an original GoF design pattern), but Church encoding has fewer moving parts. Since I was just doing an exercise, I went for the simpler implementation.
An Endpoint object should allow one of two cases: Open or Closed. To avoid primitive obsession I gave the class a private constructor:
public sealed class Endpoint<T> { private readonly T value; private readonly bool isClosed; private Endpoint(T value, bool isClosed) { this.value = value; this.isClosed = isClosed; }
Since the constructor is private you need another way to create Endpoint objects. Two factory methods provide that affordance:
public static Endpoint<T> Closed<T>(T value) { return Endpoint<T>.Closed(value); } public static Endpoint<T> Open<T>(T value) { return Endpoint<T>.Open(value); }
The heart of the Church encoding is the Match method:
public TResult Match<TResult>( Func<T, TResult> whenClosed, Func<T, TResult> whenOpen) { if (isClosed) return whenClosed(value); else return whenOpen(value); }
Such an API is an example of poka-yoke because it obliges you to deal with both cases. The compiler will keep you honest: Did you remember to deal with both the open and the closed case? When calling the Match method, you must supply both arguments, or your code doesn't compile. Make illegal states unrepresentable.
Containment #
With the Endpoint class in place, you can implement a Range class.
public sealed class Range<T> where T : IComparable<T>
It made sense to me to constrain the T type argument to IComparable<T>, although it's possible that I could have deferred that constraint to the actual Contains method, like I did with my Haskell implementation.
A Range holds two Endpoint values:
public Range(Endpoint<T> min, Endpoint<T> max) { this.min = min; this.max = max; }
The Contains method makes use of the built-in All method, using a private helper function as the predicate:
private bool IsInRange(T candidate) { return min.Match( whenClosed: l => max.Match( whenClosed: h => l.CompareTo(candidate) <= 0 && candidate.CompareTo(h) <= 0, whenOpen: h => l.CompareTo(candidate) <= 0 && candidate.CompareTo(h) < 0), whenOpen: l => max.Match( whenClosed: h => l.CompareTo(candidate) < 0 && candidate.CompareTo(h) <= 0, whenOpen: h => l.CompareTo(candidate) < 0 && candidate.CompareTo(h) < 0)); }
This implementation performs a nested Match to arrive at the appropriate answer. The code isn't as elegant or readable as its F# counterpart, but it comes with comparable compile-time safety. You can't forget a combination, because if you do, your code isn't going to compile.
Still, you can't deny that C# involves more ceremony.
Conclusion #
Once you know how, it's not that difficult to port a functional design from F# or Haskell to a language like C#. The resulting code tends to be more complicated, but to a large degree, it's possible to retain the type safety.
In this article you saw a sketch of how to make that transition, using the Range kata as an example. The resulting C# API is perfectly serviceable, as the test code demonstrates.
Now that we have covered the fundamentals of the Range kata we have learned enough about it to go beyond the exercise and examine some more abstract properties.
Next: Range as a functor.
A Range kata implementation in F#
This time with some property-based testing.
This article is an instalment in a short series of articles on the Range kata. In the previous article I described my first attempt at the kata, and also complained that I had to think of test cases myself. When I find it tedious coming up with new test cases, I usually start to wonder if it'd be easier to use property-based testing.
Thus, when I decided to revisit the kata, the variation that I was most interested in pursuing was to explore whether it would make sense to use property-based testing instead of a set of existing examples.
Since I also wanted to do the second attempt in F#, I had a choice between FsCheck and Hedgehog. Each have their strengths and weaknesses, but since I already know FsCheck so well, I decided to go with Hedgehog.
I also soon discovered that I had no interest in developing the full suite of capabilities implied by the kata. Instead, I decided to focus on just the data structure itself, as well as the contains function. As in the previous article, this function can also be used to cover the kata's ContainsRange feature.
Getting started #
There's no rule that you can't combine property-based testing with test-driven development (TDD). On the contrary, that's how I often do it. In this exercise, I first wrote this test:
[<Fact>] let ``Closed range contains list`` () = Property.check <| property { let! xs = Gen.int16 (Range.linearBounded ()) |> Gen.list (Range.linear 1 99) let min = List.min xs let max = List.max xs let actual = (Closed min, Closed max) |> Range.contains xs Assert.True (actual, sprintf "Range [%i, %i] expected to contain list." min max) }
We have to be careful when reading and understanding this code: There are two Range modules in action here!
Hedgehog comes with a Range module that you must use to define how it samples values from domains. Examples of that here are Range.linearBounded and Range.linear.
On the other hand, I've defined my contains function in a Range module, too. As long as there's no ambiguity, the F# compiler doesn't have a problem with that. Since there's no contains function in the Hedgehog Range module, the F# compiler isn't confused.
We humans, on the other hand, might be confused, and had this been a code base that I had to maintain for years, I might seriously consider whether I should rename my own Range module to something else, like Interval, perhaps.
In any case, the first test (or property, if you will) uses a technique that I often use with property-based testing. I'm still searching for a catchy name for this, but here we may call it something like reverse test-case assembly. My goal is to test a predicate, and this particular property should verify that for a given Equivalence Class, the predicate is always true.
While we may think of an Equivalence Class as a set from which we pick test cases, I don't actually have a full enumeration of such a set. I can't have that, since that set is infinitely big. Instead of randomly picking values from a set that I can't fully populate, I instead carefully pick test case values in such a way that they would all belong to the same set partition (Equivalence Class).
The test name suggests the test case: I'd like to verify that given I have a closed range, when I ask it whether a list within that range is contained, then the answer is true. How do I pick such a test case?
I do it in reverse. You can say that the sampling is the dual of the test. I start with a list (xs) and only then do I create a range that contains it. Since the first test case is for a closed range, the min and max values are sufficient to define such a range.
How do I pass that property?
Degenerately, as is often the case with TDD beginnings:
module Range = let contains _ _ = true
Even though the Closed range contains list property effectively executes a hundred test cases, the Devil's Advocate can easily ignore that and instead return hard-coded true.
More properties are required to flesh out the behaviour of the function.
Open range #
While I do keep the transformation priority premise in mind when picking the next test (or, here, property), I'm rarely particularly analytic about it. Since the first property tests that a closed range barely contains a list of values from its minimum to its maximum, it seemed like a promising next step to consider the case where the range consisted of open endpoints. That was the second test I wrote, then:
[<Fact>] let ``Open range doesn't contain endpoints`` () = Property.check <| property { let! min = Gen.int32 (Range.linearBounded ()) let! max = Gen.int32 (Range.linearBounded ()) let actual = (Open min, Open max) |> Range.contains [min; max] Assert.False (actual, sprintf "Range (%i, %i) expected not to contain list." min max) }
This property simply states that if you query the contains predicate about a list that only contains the endpoints of an open range, then the answer is false because the endpoints are Open.
One implementation that passes both tests is this one:
module Range = let contains _ endpoints = match endpoints with | Open _, Open _ -> false | _ -> true
This implementation is obviously still incorrect, but we have reason to believe that we're moving closer to something that will eventually work.
Tick-tock #
In the spirit of the transformation priority premise, I've often found that when test-driving a predicate, I seem to fall into a tick-tock pattern where I alternate between tests for a true return value, followed by a test for a false return value, or the other way around. This was also the case here. The previous test was for a false value, so the third test requires true to be returned:
[<Fact>] let ``Open range contains list`` () = Property.check <| property { let! xs = Gen.int64 (Range.linearBounded ()) |> Gen.list (Range.linear 1 99) let min = List.min xs - 1L let max = List.max xs + 1L let actual = (Open min, Open max) |> Range.contains xs Assert.True (actual, sprintf "Range (%i, %i) expected to contain list." min max) }
This then led to this implementation of the contains function:
module Range = let contains ys endpoints = match endpoints with | Open x, Open z -> ys |> List.forall (fun y -> x < y && y < z) | _ -> true
Following up on the above true-demanding test, I added one that tested a false scenario:
[<Fact>] let ``Open-closed range doesn't contain endpoints`` () = Property.check <| property { let! min = Gen.int16 (Range.linearBounded ()) let! max = Gen.int16 (Range.linearBounded ()) let actual = (Open min, Closed max) |> Range.contains [min; max] Assert.False (actual, sprintf "Range (%i, %i] expected not to contain list." min max) }
This again led to this implementation:
module Range = let contains ys endpoints = match endpoints with | Open x, Open z -> ys |> List.forall (fun y -> x < y && y < z) | Open x, Closed z -> false | _ -> true
I had to add four more tests before I felt confident that I had the right implementation. I'm not going to show them all here, but you can look at the repository on GitHub if you're interested in the interim steps.
Types and functionality #
So far I had treated a range as a pair (two-tuple), just as I had done with the code in my first attempt. I did, however, have a few other things planned for this code base, so I introduced a set of explicit types:
type Endpoint<'a> = Open of 'a | Closed of 'a type Range<'a> = { LowerBound : Endpoint<'a>; UpperBound : Endpoint<'a> }
The Range record type is isomorphic to a pair of Endpoint values, so it's not strictly required, but does make things more explicit.
To support the new type, I added an ofEndpoints function, and finalized the implementation of contains:
module Range = let ofEndpoints (lowerBound, upperBound) = { LowerBound = lowerBound; UpperBound = upperBound } let contains ys r = match r.LowerBound, r.UpperBound with | Open x, Open z -> ys |> List.forall (fun y -> x < y && y < z) | Open x, Closed z -> ys |> List.forall (fun y -> x < y && y <= z) | Closed x, Open z -> ys |> List.forall (fun y -> x <= y && y < z) | Closed x, Closed z -> ys |> List.forall (fun y -> x <= y && y <= z)
As is so often the case in F#, pattern matching makes such functions a pleasure to implement.
Conclusion #
I was curious whether using property-based testing would make the development process of the Range kata simpler. While each property was simple, I still had to write eight of them before I felt I'd fully described the problem. This doesn't seem like much of an improvement over the example-driven approach I took the first time around. It seems to be a comparable amount of code, and on one hand a property is more abstract than an example, but on the hand usually also covers more ground. I feel more confident that this implementation works, because I know that it's being exercised more rigorously.
When I find myself writing a property per branch, so to speak, I always feel that I missed a better way to describe the problem. As an example, for years I would demonstrate how to test the FizzBuzz kata with property-based testing by dividing the problem into Equivalence Classes and then writing a property for each partition. Just as I've done here. This is usually possible, but smells of being too coupled to the implementation.
Sometimes, if you think about the problem long enough, you may be able to produce an alternative set of properties that describe the problem in a way that's entirely decoupled from the implementation. After years, I finally managed to do that with the FizzBuzz kata.
I didn't succeed doing that with the Range kata this time around, but maybe later.
A Range kata implementation in Haskell
A first crack at the exercise.
This article is an instalment in a short series of articles on the Range kata. Here I describe my first attempt at the exercise. As I usually advise people on doing katas, the first time you try your hand at a kata, use the language with which you're most comfortable. To be honest, I may be most habituated to C#, having programmed in it since 2002, but on the other hand, I currently 'think in Haskell', and am often frustrated with C#'s lack of structural equality, higher-order abstractions, and support for functional expressions.
Thus, I usually start with Haskell even though I always find myself struggling with the ecosystem. If you do, too, the source code is available on GitHub.
I took my own advice by setting out with the explicit intent to follow the Range kata description as closely as possible. This kata doesn't beat about the bush, but instead just dumps a set of test cases on you. It wasn't clear if this is the most useful set of tests, or whether the order in which they're represented is the one most conducive to a good experience of test-driven development, but there was only one way to find out.
I quickly learned, however, that the suggested test cases were insufficient in describing the behaviour in enough details.
Containment #
I started by adding the first two test cases as inlined HUnit test lists:
"integer range contains" ~: do (r, candidate, expected) <- [ ((Closed 2, Open 6), [2,4], True), ((Closed 2, Open 6), [-1,1,6,10], False) ] let actual = r `contains` candidate return $ expected ~=? actual
I wasn't particularly keen on going full Devil's Advocate on the exercise. I could, on the other hand, trivially pass both tests with this obviously degenerate implementation:
import Data.List data Endpoint a = Open a | Closed a deriving (Eq, Show) contains _ candidate = [2] `isPrefixOf` candidate
Reluctantly, I had to invent some additional test cases:
"integer range contains" ~: do (r, candidate, expected) <- [ ((Closed 2 , Open 6), [2,4], True), ((Closed 2 , Open 6), [-1,1,6,10], False), ((Closed (-1), Closed 10), [-1,1,6,10], True), ((Closed (-1), Open 10), [-1,1,6,10], False), ((Closed (-1), Open 10), [-1,1,6,9], True), (( Open 2, Closed 6), [3,5,6], True), (( Open 2, Open 6), [2,5], False), (( Open 2, Open 6), [], True), ((Closed 2, Closed 6), [3,7,4], False) ] let actual = r `contains` candidate return $ expected ~=? actual
This was when I began to wonder whether it would have been easier to use property-based testing. That would entail, however, a departure from the kata's suggested test cases, so I decided to stick to the plan and then perhaps return to property-based testing when repeating the exercise.
Ultimately I implemented the contains function this way:
contains :: (Foldable t, Ord a) => (Endpoint a, Endpoint a) -> t a -> Bool contains (lowerBound, upperBound) = let isHighEnough = case lowerBound of Closed x -> (x <=) Open x -> (x <) isLowEnough = case upperBound of Closed y -> (<= y) Open y -> (< y) isContained x = isHighEnough x && isLowEnough x in all isContained
In some ways it seems a bit verbose to me, but I couldn't easily think of a simpler implementation.
One of the features I find so fascinating about Haskell is how general it enables me to be. While the tests use integers for concision, the contains function works with any Ord instance; not only Integer, but also Double, Word, Day, TimeOfDay, or some new type I can't even predict.
All points #
The next function suggested by the kata is a function to enumerate all points in a range. There's only a single test case, so again I added some more:
"getAllPoints" ~: do (r, expected) <- [ ((Closed 2, Open 6), [2..5]), ((Closed 4, Open 8), [4..7]), ((Closed 2, Closed 6), [2..6]), ((Closed 4, Closed 8), [4..8]), (( Open 2, Closed 6), [3..6]), (( Open 4, Closed 8), [5..8]), (( Open 2, Open 6), [3..5]), (( Open 4, Open 8), [5..7]) ] let actual = allPoints r return $ expected ~=? actual
Ultimately, after I'd implemented the next feature, I refactored the allPoints function to make use of it, and it became a simple one-liner:
allPoints :: (Enum a, Num a) => (Endpoint a, Endpoint a) -> [a] allPoints = uncurry enumFromTo . endpoints
The allPoints function also enabled me to express the kata's ContainsRange test cases without introducing a new API:
"ContainsRange" ~: do (r, candidate, expected) <- [ ((Closed 2, Open 5), allPoints (Closed 7, Open 10), False), ((Closed 2, Open 5), allPoints (Closed 3, Open 10), False), ((Closed 3, Open 5), allPoints (Closed 2, Open 10), False), ((Closed 2, Open 10), allPoints (Closed 3, Closed 5), True), ((Closed 3, Closed 5), allPoints (Closed 3, Open 5), True) ] let actual = r `contains` candidate return $ expected ~=? actual
As I've already mentioned, the above implementation of allPoints is based on the next feature, endpoints.
Endpoints #
The kata also suggests a function to return the two endpoints of a range, as well as some test cases to describe it. Once more, I had to add more test cases to adequately describe the desired functionality:
"endPoints" ~: do (r, expected) <- [ ((Closed 2, Open 6), (2, 5)), ((Closed 1, Open 7), (1, 6)), ((Closed 2, Closed 6), (2, 6)), ((Closed 1, Closed 7), (1, 7)), (( Open 2, Open 6), (3, 5)), (( Open 1, Open 7), (2, 6)), (( Open 2, Closed 6), (3, 6)), (( Open 1, Closed 7), (2, 7)) ] let actual = endpoints r return $ expected ~=? actual
The implementation is fairly trivial:
endpoints :: (Num a1, Num a2) => (Endpoint a2, Endpoint a1) -> (a2, a1) endpoints (Closed x, Closed y) = (x , y) endpoints (Closed x, Open y) = (x , y-1) endpoints ( Open x, Closed y) = (x+1, y) endpoints ( Open x, Open y) = (x+1, y-1)
One attractive quality of algebraic data types is that the 'algebra' of the type(s) tell you how many cases you need to pattern-match against. Since I'm treating a range as a pair of Endpoint values, and since each Endpoint can be one of two cases (Open or Closed), there's exactly 2 * 2 = 4 possible combinations (since a tuple is a product type).
That fits with the number of pattern-matches required to implement the function.
Overlapping ranges #
The final interesting feature is a predicate to determine whether one range overlaps another. As has become a refrain by now, I didn't find the suggested test cases sufficient to describe the desired behaviour, so I had to add a few more:
"overlapsRange" ~: do (r, candidate, expected) <- [ ((Closed 2, Open 5), (Closed 7, Open 10), False), ((Closed 2, Open 10), (Closed 3, Open 5), True), ((Closed 3, Open 5), (Closed 3, Open 5), True), ((Closed 2, Open 5), (Closed 3, Open 10), True), ((Closed 3, Open 5), (Closed 2, Open 10), True), ((Closed 3, Open 5), (Closed 1, Open 3), False), ((Closed 3, Open 5), (Closed 5, Open 7), False) ] let actual = r `overlaps` candidate return $ expected ~=? actual
I'm not entirely happy with the implementation:
overlaps :: (Ord a1, Ord a2) => (Endpoint a1, Endpoint a2) -> (Endpoint a2, Endpoint a1) -> Bool overlaps (l1, h1) (l2, h2) = let less (Closed x) (Closed y) = x <= y less (Closed x) (Open y) = x < y less (Open x) (Closed y) = x < y less (Open x) (Open y) = x < y in l1 `less` h2 && l2 `less` h1
Noth that the code presented here is problematic in isolation, but if you compare it to the above contains function, there seems to be some repetition going on. Still, it's not quite the same, but the code looks similar enough that it bothers me. I feel that some kind of abstraction is sitting there, right before my nose, mocking me because I can't see it. Still, the code isn't completely duplicated, and even if it was, I can always invoke the rule of three and let it remain as it is.
Which is ultimately what I did.
Equality #
The kata also suggests some test cases to verify that it's possible to compare two ranges for equality. Dutifully I added those test cases to the code base, even though I knew that they'd automatically pass.
"Equals" ~: do (x, y, expected) <- [ ((Closed 3, Open 5), (Closed 3, Open 5), True), ((Closed 2, Open 10), (Closed 3, Open 5), False), ((Closed 2, Open 5), (Closed 3, Open 10), False), ((Closed 3, Open 5), (Closed 2, Open 10), False) ] let actual = x == y return $ expected ~=? actual
In the beginning of this article, I called attention to C#'s regrettable lack of structural equality. Here's an example of what I mean. In Haskell, these tests automatically pass because Endpoint is an Eq instance (by declaration), and all pairs of Eq instances are themselves Eq instances. Simple, elegant, powerful.
Conclusion #
As a first pass at the (admittedly uncomplicated) Range kata, I tried to follow the 'plan' implied by the kata description's test cases. I quickly became frustrated with their lack of completion. They were adequate in indicating to a human (me) what the desired behaviour should be, but insufficient to satisfactorily describe the desired behaviour.
I could, of course, have stuck with only those test cases, and instead of employing the Devil's Advocate technique (which I actively tried to avoid) made an honest effort to implement the functionality.
The things is, however, that I don't trust myself. At its essence, the Range kata is all about edge cases, which are where most bugs tend to lurk. Thus, these are exactly the cases that should be covered by tests.
Having made enough 'dumb' programming mistakes during my career, I didn't trust myself to be able to write correct implementations without more test coverage than originally suggested. That's the reason I added more tests.
On the other hand, I more than once speculated whether property-based testing would make this work easier. I decided to pursue that idea during my second pass at the kata.

Comments
I’d have another test case for the Equality function:
((Open 2, Open 6), (Closed 3, Closed 5), True). While it is nice Haskell provides (automatic) structural equality, I don’t think we want to say that the (2, 6) range (on integers!) is something else than the [3, 5] range.But yes, this opens a can of worms: While (2, 6) = [3, 5] on integers, (2.0, 6.0) is obviously different than [3.0, 5.0] (on reals/Doubles/…). I have no idea: In Haskell, could you write an implementation of a function which would behave differently depending on whether the type argument belongs to a typeclass or not?
Petr, thank you for writing. I don't think I'd add that (or similar) test cases, but it's a judgment call, and it's partly language-specific. What you're suggesting is to consider things that are equivalent equal. I agree that for integers this would be the case, but it wouldn't be for rational numbers, or floating points (or real numbers, if we had those in programming).
In Haskell it wouldn't really be idiomatic, because equality is defined by the
Eqtype class, and most types just go with the default implementation. What you suggest requires writing an explicitEqinstance forEndpoint. It'd be possible, but then you'd have to deal explicitly with the various integer representations separately from other representations that use floating points.The distinction between equivalence and equality is largely artificial or a convenient hand wave. To explain what I mean, consider mathematical expressions. Obviously, 3 + 1 is equal to 2 + 2 when evaluated, but they're different expressions. Thus, on an expression level, we don't consider those two expressions equal. I think of the integer ranges (2, 6) and [3, 6] the same way. They evaluate to the same, but there aren't equal.
I don't think that this is a strong argument, mind. In other programming languages, I might arrive at a different decision. It also matters what client code needs to do with the API. In any case, the decision to not consider equivalence the same as equality is congruent with how Haskell works.
The existence of floating points and rational numbers, however, opens another can of worms that I happily glossed over, since I had a completely different goal with the kata than producing a reusable library.
Haskell actually supports rational numbers with the
%operator:This value represents ½, to be explicit.
Unfortunately, according to the specification (or, at least, the documentation) of the
Enumtype class, the two 'movement' operationssuccandpredjump by increments of 1:The same is the case with floating points:
This is unfortunate when it comes to floating points, since it would be possible to enumerate all floating points in a range. (For example, if a single-precision floating point occupies 32 bits, there's a finite number of them, and you can enumerate them.)
As Sonat Süer points out, this means that the
allPointsfunction is fundamentally broken for floating points and rational numbers (and possibly other types as well).One way around that in Haskell would be to introduce a new type class for the purpose of truly enumerating ranges, and either implement it correctly for floating points, or explicitly avoid making
FloatandDoubleinstances of that new type class. This, on the other hand, would have the downside that all of a sudden, theallPointsfunction wouldn't support any custom type of which I, as the implementer, is unaware.If this was a library that I'd actually have to ship as a reusable API, I think I'd start by not including the
allPointsfunction, and then see if anyone asks for it. If or when that happens, I'd begin a process to chart why people need it, and what could be done to serve those needs in a useful and mathematically consistent manner.