ploeh blog danish software design
Geographic hulls
Seven lines of Python code.
Can you tell what this is?
I showed this to both my wife and my son, and they immediately recognized it for what it is. On the other hand, they're also both culturally primed for it.
After all, it's a map of Denmark, although I've transformed each of the major islands, as well as the peninsula of Jutland to their convex hulls.
Here's the original map I used for the transformation:
I had a reason to do this, having to do with the coastline paradox, but my underlying motivation isn't really that important for this article, since I rather want to discuss how I did it.
The short answer is that I used Python. You have to admit that Python has a fabulous ecosystem for all kinds of data crunching, including visualizations. I'd actually geared up to implementing a Graham scan myself, but that turned out not to be necessary.
GeoPandas to the rescue #
I'm a novice Python programmer, but I've used Matplotlib before to visualize data, so I found it natural to start with a few web searches to figure out how to get to grips with the problem.
I quickly found GeoPandas, which works on top of Matplotlib to render and visualize geographical data.
My next problem was to find a data set for Denmark, which I found on SimpleMaps. I chose to download and work with the GeoJSON format.
Originally, I'd envisioned implementing a Graham scan myself. After all, I'd done that before in F#, and it's a compelling exercise. It turned out, however, that this function is already available in the GeoPandas API.
I had trouble separating the data file's multi-part geometry into multiple single geometries. This meant that when I tried to find the convex hull, I got the hull of the entire map, instead of each island individually. The solution was to use the explode function.
Once I figured that out, it turned out that all I needed was seven lines of Python code, including imports and a blank line:
import geopandas as gpd import matplotlib.pyplot as plt map = gpd.read_file('dk.json') map.explode().boundary.plot(edgecolor='green').set_axis_off() map.explode().convex_hull.boundary.plot().set_axis_off() plt.show()
In this script, I display the unmodified map before the convex hulls. This is only an artefact of my process. As I've already admitted, this is new ground for me, and I initially wanted to verify that I could even read in and display a GeoJSON file.
For both maps I use the boundary property to draw only the outline of the map, rather than filled polygons.
Enveloping the map parts #
Mostly for fun, but also to illustrate what a convex hull is, we can layer the two visualizations in a single image. In order to do that, a few changes to the code are required.
import geopandas as gpd import matplotlib.pyplot as plt map = gpd.read_file('dk.json') _, ax = plt.subplots() map.explode().boundary.plot(ax=ax, edgecolor='green').set_axis_off() map.explode().convex_hull.boundary.plot(ax=ax).set_axis_off() plt.show()
This little script now produces this image:
Those readers who know Danish geography may wonder what's going on with Falster. Since it's the sixth-largest Island in Denmark, shouldn't it have its own convex hull? Yes, it should, yet here it's connected to Zealand. Granted, two bridges connect the two, but that's hardly sufficient to consider them one island. There are plenty of bridges in Denmark, so according to that criterion, most of Denmark is connected. In fact, on the above map, only Bornholm, Samsø, Læsø, Ærø, Fanø, and Anholt would then remain as islands.
Rather, this only highlights the quality, or lack thereof, of the data set. I don't want to complain about a free resource, and the data set has served my purposes well enough. I mostly point this out in case readers were puzzled about this. In fact, a similar case applies to Nørrejyske Ø, which in the GeoJSON map is connected to Jutland at Aalborg. Yes, there's a bridge there. No, that shouldn't qualify as a land connection.
Other countries #
As you may have noticed, apart from the hard-coded file name, nothing in the code is specific to Denmark. This means that you can play around with other countries. Here I've downloaded various GeoJSON data sets from GeoJSON Maps of the globe, which seems to be using the same source data set that the Danish data set is also based on. In other words, if I download the file for Denmark from that site, it looks exactly as above.
Can you guess which country this is?
Or this one?
While this is all good fun, not all countries have interesting convex hull:
While I'll let you have a bit of fun guessing, you can hover your cursor over each image to reveal which country it is.
Conclusion #
Your default position when working with Python should probably be: There's already a library for that.
In this article, I've described how I wanted to show Denmark, but only the convex hull of each of the larger islands, as well as the Jutland peninsula. Of course, there was already a library for that, so that I only needed to write seven lines of code to produce the figures I wanted.
Granted, it took a few hours of research to put those seven lines together, but I'm only a novice Python programmer, and I'm sure an old hand could do it much faster.
Modelling data relationships with C# types
A C# example implementation of Ghosts of Departed Proofs.
This article continues where Modelling data relationships with F# types left off. It ports the F# example code to C#. If you don't read F# source code, you may instead want to read Implementing rod-cutting to get a sense of the problem being addressed.
I'm going to assume that you've read enough of the previous articles to get a sense of the example, but in short, this article examines if it's possible to use the type system to model data relationships. Specifically, we have methods that operate on a collection and a number. The precondition for calling these methods is that the number is a valid (one-based) index into the collection.
While you would typically implement such a precondition with a Guard Clause and communicate it via documentation, you can also use the Ghosts of Departed Proofs technique to instead leverage the type system. Please see the previous article for an overview.
That said, I'll repeat one point here: The purpose of these articles is to showcase a technique, using a simple example to make it, I hope, sufficiently clear what's going on. All this machinery is hardly warranted for an example as simple as this. All of this is a demonstration, not a recommendation.
Size proofs #
As in the previous article, we may start by defining what a 'size proof' looks like. In C#, it may idiomatically be a class with an internal constructor.
public sealed class Size<T> { public int Value { get; } internal Size(int value) { Value = value; } // Also override ToString, Equals, and GetHashCode... }
Since the constructor is internal it means that client code can't create Size<T> instances, and thereby client code can't decide a concrete type for the phantom type T.
Issuing size proofs #
How may client code create Size<T> objects? It may ask a PriceList<T> object to issue a proof:
public sealed class PriceList<T> { public IReadOnlyCollection<int> Prices { get; } internal PriceList(IReadOnlyCollection<int> prices) { Prices = prices; } public Size<T>? TryCreateSize(int candidate) { if (0 < candidate && candidate <= Prices.Count) return new Size<T>(candidate); else return null; } // More members go here...
If the requested candidate integer represents a valid (one-indexed) position in the PriceList<T> object, the return value is a Size<T> object that contains the candidate. If, on the other hand, the candidate isn't in the valid range, no object is returned.
Since both PriceList<T> and Size<T> classes are immutable, once a 'size proof' has been issued, it remains valid. As I've previously argued, immutability makes encapsulation simpler.
This kind of API does, however, look like it's turtles all the way down. After all, the PriceList<T> constructor is also internal. Now the question becomes: How does client code create PriceList<T> objects?
The short answer is that it doesn't. Instead, it'll be given an object by the library API. You'll see how that works later, but first, let's review what such an API enables us to express.
Proof-based Cut API #
As described in Encapsulating rod-cutting, returning a collection of 'cut' objects better communicates postconditions than returning a tuple of two arrays, as the original algorithm suggested. In other words, we're going to need a type for that.
public sealed record Cut<T>(int Revenue, Size<T> Size);
In this case we can get by with a simple record type. Since one of the properties is of the type Size<T>, client code can't create Cut<T> instances, just like it can't create Size<T> or PriceList<T> objects. This is what we want, because a Cut<T> object encapsulates a proof that it's valid, related to the original collection of prices.
We can now define the Cut method as an instance method on PriceList<T>. Notice how all the T type arguments line up. As input, the Cut method only accepts Size<T> proofs issued by a compatible price list. This is enforced at compile time, not at run time.
public IReadOnlyCollection<Cut<T>> Cut(Size<T> n) { var p = Prices.Prepend(0).ToArray(); var r = new int[n.Value + 1]; var s = new int[n.Value + 1]; r[0] = 0; for (int j = 1; j <= n.Value; j++) { var q = int.MinValue; for (int i = 1; i <= j; i++) { var candidate = p[i] + r[j - i]; if (q < candidate) { q = candidate; s[j] = i; } } r[j] = q; } var cuts = new List<Cut<T>>(); for (int i = 1; i <= n.Value; i++) { var revenue = r[i]; var size = new Size<T>(s[i]); cuts.Add(new Cut<T>(revenue, size)); } return cuts; }
For good measure, I'm showing the entire implementation, but you only need to pay attention to the method signature. The point is that n is constrained by the type system to be in a valid range.
Proof-based Solve API #
The same technique can be applied to the Solve method. Just align the Ts.
public IReadOnlyCollection<Size<T>> Solve(Size<T> n) { var cuts = Cut(n).ToArray(); var sizes = new List<Size<T>>(); var size = n; while (size.Value > 0) { sizes.Add(cuts[size.Value - 1].Size); size = new Size<T>(size.Value - cuts[size.Value - 1].Size.Value); } return sizes; }
This is another instance method on PriceList<T>, which is where T is defined.
Proof-based revenue API #
Finally, we may also implement a method to calculate the revenue from a given sequence of cuts.
public int CalculateRevenue(IReadOnlyCollection<Size<T>> cuts) { var arr = Prices.ToArray(); return cuts.Sum(c => arr[c.Value - 1]); }
Not surprisingly, I hope, CalculateRevenue is another instance method on PriceList<T>. The cuts will typically come from a call to Solve, but it's entirely possible for client code to create an ad-hoc collection of Size<T> objects by repeatedly calling TryCreateSize.
Running client code #
How does client code use this API? It calls an Accept method with an implementation of this interface:
public interface IPriceListVisitor<TResult> { TResult Visit<T>(PriceList<T> priceList); }
Why 'visitor'? This doesn't quite look like a Visitor, and yet, it still does.
Imagine, for a moment, that we could enumerate all types that T could inhabit.
TResult Visit(PriceList<Type1> priceList); TResult Visit(PriceList<Type2> priceList); TResult Visit(PriceList<Type3> priceList); // ⋮ TResult Visit(PriceList<TypeN> priceList);
Clearly we can't do that, since T is infinite, but if we could, the interface would look like a Visitor.
I find the situation sufficiently similar to name the interface with the Visitor suffix. Now we only need a class with an Accept method.
public sealed class RodCutter(IReadOnlyCollection<int> prices) { public TResult Accept<TResult>(IPriceListVisitor<TResult> visitor) { return visitor.Visit(new PriceList<object>(prices)); } }
Client code may create a RodCutter object, as well as one or more classes that implement IPriceListVisitor<TResult>, and in this way interact with the library API.
Let's see some examples. We'll start with the original CLRS example, written as an xUnit.net test.
[Fact] public void ClrsExample() { var sut = new RodCutter([1, 5, 8, 9, 10, 17, 17, 20, 24, 30]); var actual = sut.Accept(new CutRodVisitor(10)); var expected = new[] { ( 1, 1), ( 5, 2), ( 8, 3), (10, 2), (13, 2), (17, 6), (18, 1), (22, 2), (25, 3), (30, 10) }; Assert.Equal(expected, actual); }
CutRodVisitor is a nested class that implements the IPriceListVisitor<TResult> interface:
private class CutRodVisitor(int i) : IPriceListVisitor<IReadOnlyCollection<(int, int)>> { public IReadOnlyCollection<(int, int)> Visit<T>(PriceList<T> priceList) { var n = priceList.TryCreateSize(i); if (n is null) return []; else { var cuts = priceList.Cut(n); return cuts.Select(c => (c.Revenue, c.Size.Value)).ToArray(); } } }
The CutRodVisitor class returns a collection of tuples. Why doesn't it just return cuts directly?
It can't, because it wouldn't type-check. Think about it for a moment. When you implement the interface, you need to pick a type for TResult. You can't, however, declare it to implement IPriceListVisitor<Cut<T>> (where T would be the T from Visit<T>), because at the class level, you don't know what T is. Neither does the compiler.
Your Visit<T> implementation must work for any T.
Preventing misalignment #
Finally, here's a demonstration of how the phantom type prevents confusing or mixing up two (or more) different price lists. Consider this rather artificial example:
[Fact] public void NestTwoSolutions() { var sut = new RodCutter([1, 2, 2]); var inner = new RodCutter([1]); (int, int)? actual = sut.Accept(new NestedRevenueVisitor(inner)); Assert.Equal((3, 1), actual); }
This unit test creates two price arrays and calls Accept on one of them (the 'outer' one, you may say), while passing the inner one to the Visitor, which at first glance just looks like this:
private class NestedRevenueVisitor(RodCutter inner) : IPriceListVisitor<(int, int)?> { public (int, int)? Visit<T>(PriceList<T> priceList) { return inner.Accept(new InnerRevenueVisitor<T>(priceList)); } // Inner visitor goes here... }
Notice that it only delegates to yet another Visitor, passing the 'outer' priceList as a constructor parameter to the next Visitor. The purpose of this is to bring two PriceList<T> objects in scope at the same time. This will enable us to examine what happens if we make a programming mistake.
First, however, here's the proper, working implementation without mistakes:
private class InnerRevenueVisitor<T>(PriceList<T> priceList1) : IPriceListVisitor<(int, int)?> { public (int, int)? Visit<T1>(PriceList<T1> priceList2) { var n1 = priceList1.TryCreateSize(3); if (n1 is null) return null; else { var cuts1 = priceList1.Solve(n1); var revenue1 = priceList1.CalculateRevenue(cuts1); var n2 = priceList2.TryCreateSize(1); if (n2 is null) return null; else { var cuts2 = priceList2.Solve(n2); var revenue2 = priceList2.CalculateRevenue(cuts2); return (revenue1, revenue2); } } } }
Notice how both priceList1 and priceList2 are now both in scope. So far, they're not mixed up, so the Visit implementation queries first one and then another for the optimal revenue. If all works well (which it does), it returns a tuple with the two revenues.
What happens if I make a mistake? What if, for example, I write priceList2.Solve(n1)? It shouldn't be possible to use n1, which was issued by pricelist1, with priceList2. And indeed this isn't possible. With that mistake, the code doesn't compile. The compiler error is:
Argument 1: cannot convert from 'Ploeh.Samples.RodCutting.Size<T>' to 'Ploeh.Samples.RodCutting.Size<T1>'
When you look at the types, that makes sense. After all, there's no guarantee that T is equal to T1.
You'll run into similar problems if you mix up the two 'contexts' in other ways. The code doesn't compile. Which is what you want.
Conclusion #
This article demonstrates how to use the Ghosts of Departed Proofs technique in C#. In some ways, I find that it comes across as more idiomatic in C# than in F#. I think this is because rank-2 polymorphism is only possible in F# when using its object-oriented features. Since F# is a functional-first programming language, it seems a little out of place there, whereas it looks more at home in C#.
Perhaps I should have designed the F# code to make use of objects to the same degree as I've done here in C#.
I think I actually like how the C# API turned out, although having to define and implement a class every time you need to supply a Visitor may feel a bit cumbersome. Even so, developer experience shouldn't be exclusively about saving a few keystrokes. After all, typing isn't a bottleneck.
Dependency inversion without inversion of control
Here, have a sandwich.
For years I've been thinking about the Dependency Inversion Principle (DIP) and Inversion of Control (IoC) as two different things. While there's some overlap, they're not the same. To make matters more confusing, most people seem to consider IoC and Dependency Injection (DI) as interchangeable synonyms. As Steven van Deursen and I explain in DIPPP, they're not the same.
I recently found myself in a discussion on Stack Overflow where I was trying to untangle that confusion for a fellow Stack Overflow user. While I hadn't included a pedagogical Venn diagram, perhaps I should have.
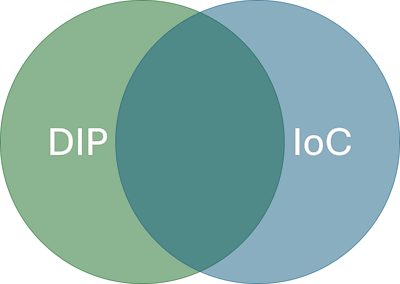
This figure suggests that the sets are of equal size, which doesn't have to be the case. The point, rather, is that while the intersection may be substantial, each relative complement is not only not empty, but richly populated.
In this article, I'm not going to spend more time on the complement IoC without DIP. Rather, I'll expand on how to apply the DIP without IoC.
Appeal to authority? #
While writing the Stack Overflow answer, I'd tried to keep citations to 'original sources'. Sometimes, when a problem is technically concrete, it makes sense for me to link to one of my own works, but I've found that when the discussion is more abstract, that rarely helps convincing people. That's understandable. I'd also be sceptical if I were to run into some rando that immediately proceeded to argue a case by linking to his or her own blog.
This strategy, however elicited this response:
"Are you aware of any DIP-compliant example from Robert Martin that does not utilize polymorphism? The original paper along with some of Martin's lectures certainly seem to imply the DIP requires polymorphism."
That's a fair question, and once I started looking for such examples, I had to admit that I couldn't find any. Eventually, I asked Robert C. Martin directly.
"Does the DIP require polymorphism? I argue that it does't, but I've managed to entangle myself in a debate where original sources count. Could you help us out?"
To which he answered in much detail, but of which the essential response was:
"The DIP does not require polymorphism. Polymorphism is just one of several mechanisms to achieve dependency inversion."
While this was the answer I'd hoped for, it's easy to dismiss this exchange as an appeal to authority. On the other hand, as Carl Sagan said, "If you wish to make an apple pie from scratch, you must first invent the universe," which obviously isn't practical, and so we instead stand on the shoulders of giants.
In this context, asking Robert C. Martin was relevant because he's the original author of works that introduce the DIP. It's reasonable to assume that he has relevant insights on the topic.
It's not that I can't argue my case independently, but rather that I didn't think that the comments section of a Stack Overflow question was the right place to do that. This blog, on the other hand, is mine, I can use all the words I'd like, and I'll now proceed to do so.
Kernel of the idea #
All of Robert C. Martin's treatments of the DIP that I've found starts with the general idea and then proceeds to show examples of implementing it in code. As I've already mentioned, I haven't found a text of Martin's where the example doesn't utilize IoC.
The central idea, however, says nothing about IoC.
"A. High-level modules should not depend on low-level modules. Both should depend on abstractions.
"B. Abstractions should not depend on details. Details should depend upon abstractions."
While only Martin knows what he actually meant, I can attempt a congenial reading of the work. What is most important here, I think, is that the word abstraction doesn't have to denote a particular kind of language construct, such as an abstract class or interface. Rather,
"Abstraction is the elimination of the irrelevant and the amplification of the essential."
The same connotation of abstraction seems to apply to the definition of the DIP. If, for example, we imagine that we consider a Domain Model, the business logic, as the essence we'd like to amplify, we may rightfully consider a particular persistence mechanism a detail. Even more concretely, if you want to take restaurant reservations via a REST API, the business rules that determine whether or not you can accept a reservation shouldn't depend on a particular database technology.
While code examples are useful, there's evidently a risk that if the examples are too much alike, it may constrain readers' thinking. All Martin's examples seem to involve IoC, but for years now, I've mostly been interested in the Dependency Inversion Principle itself. Abstractions should not depend on details. That's the kernel of the idea.
IoC isn't functional #
My thinking was probably helped along by exploring functional programming (FP). A natural question arises when one embarks on learning FP: How does IoC fit with FP? The short answer, it turns out, is that it doesn't. DI, at least, makes everything impure.
Does this mean, then, that FP precludes the DIP? That would be a problem, since the notion that abstractions shouldn't depend on details seems important. Doing FP shouldn't entail giving up on important architectural rules. And fortunately, it turns out not being the case. Quite the contrary, a consistent application of functional architecture seems to lead to Ports and Adapters. It'd go against the grain of FP to have a Domain Model query a relational database. Even if abstracted away, a database exists outside the process space of an application, and is inherently impure. IoC doesn't address that concern.
In FP, there are other ways to address such problems.
DIP sandwich #
While you can always model pure interactions with free monads, it's usually not necessary. In most cases, an Impureim Sandwich suffices.
The sample code base that accompanies Code That Fits in Your Head takes a similar approach. While it's possible to refactor it to an explicit Impureim Sandwich, the code presented in the book follows the kindred notion of Functional Core, Imperative Shell.
The code base implements an online restaurant reservation system, and the Domain Model is a set of data structures and pure functions that operate on them. The central and most complex function is the WillAccept method shown here. It decides whether to accept a reservation request, based on restaurant table configurations, existing reservations, business rules related to seating durations, etc. It does this without depending on details. It doesn't know about databases, the application's configuration system, or how to send emails in case it decides to accept a reservation.
All of this is handled by the application's HTTP Model, using the demarcation shown in Decomposing CTFiYH's sample code base. The HTTP Model defines Controllers, Data Transfer Objects (DTOs), middleware, and other building blocks required to drive the actual REST API.
The ReservationsController class contains, among many other methods, this helper method that illustrates the point:
private async Task<ActionResult> TryCreate(Restaurant restaurant, Reservation reservation) { using var scope = new TransactionScope(TransactionScopeAsyncFlowOption.Enabled); var reservations = await Repository.ReadReservations(restaurant.Id, reservation.At); var now = Clock.GetCurrentDateTime(); if (!restaurant.MaitreD.WillAccept(now, reservations, reservation)) return NoTables500InternalServerError(); await Repository.Create(restaurant.Id, reservation); scope.Complete(); return Reservation201Created(restaurant.Id, reservation); }
Notice the call to restaurant.MaitreD.WillAccept. The Controller gathers all data required to call the pure function and subsequently acts on the return value. This keeps the abstraction (MaitreD) free of implementation details.
DI addressing another concern #
You may be wondering what exactly Repository is. If you've bought the book, you also have access to the sample code base, in which case you'd be able to look it up. It turns out that it's an injected dependency. While this may seem a bit contradictory, it also gives me the opportunity to discuss that this isn't an all-or-nothing proposition.
Consider the architecture diagram from Decomposing CTFiYH's sample code base, repeated here for convenience:
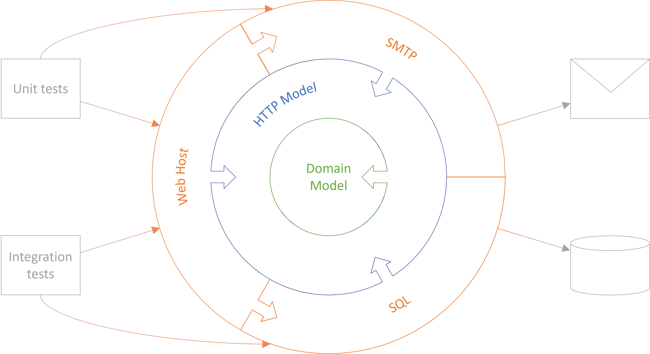
In the context of this diagram, the DIP is being applied in two different ways. From the outer Web Host to the HTTP Model, the decomposed code base uses ordinary DI. From the HTTP Model to the Domain Model, there's no inversion of control, but rather the important essence of the DIP: That the Domain Model doesn't depend on any of the details that surrounds it. Even so, the dependencies remain inverted, as indicated by the arrows.
What little DI that's left remains to support automated testing. Injecting Repository and a few other real dependencies enabled me to test-drive the externally visible behaviour of the system with state-based self-hosted tests.
If I hadn't cared about that, I could have hard-coded the SqlReservationsRepository object directly into the Controller and merged the Web Host with the HTTP Module. The Web Host is quite minimal anyway. This would, of course, have meant that the DIP no longer applied at that level, but even so, the interaction between the HTTP Model and the Domain Model would still follow the principle.
One important point about the above figure is that it's not to scale. The Web Host is in reality just six small classes, and the SQL and SMTP libraries each only contain a single class.
Conclusion #
Despite the name similarity, the Dependency Inversion Principle isn't equivalent with Inversion of Control or Dependency Injection. There's a sizeable intersection between the two, but the DIP doesn't require IoC.
I often use the Functional Core, Imperative Shell architecture, or the Impureim Sandwich pattern to invert the dependencies without inverting control. This keeps most of my code more functional, which also means that it fits better in my head and is intrinsically testable.
Modelling data relationships with F# types
An F# example implementation of Ghosts of Departed Proofs.
In a previous article, Encapsulating rod-cutting, I used a code example to discuss how to communicate an API's contract to client developers; that is, users of the API. In the article, I wrote
"All this said, however, it's also possible that I'm missing an obvious design alternative. If you can think of a way to model this relationship in a non-predicative way, please write a comment."
And indeed, a reader helpfully offered an alternative:
"Regarding the relation between the array and the index, you will find the paper called "Ghosts of departed proofs" interesting. Maybe an overkill in this case, maybe not, but a very interesting and useful technique in general."
I wouldn't call it 'an obvious design alternative', but nonetheless find it interesting. In this article, I'll pick up the code from Encapsulating rod-cutting and show how the 'Ghosts of Departed Proofs' (GDP) technique may be applied.
Problem review #
Before we start with the GDP technique, a brief review of the problem is in order. For the complete overview, you should read the Encapsulating rod-cutting article. In the present article, however, we'll focus on one particular problem related to encapsulation:
Ideally, the cut function should take two input arguments. The first argument, p, is an array or list of prices. The second argument, n, is the size of a rod to cut optimally. One precondition states that n must be less than or equal to the length of p. This is because the algorithm needs to look up the price of a rod of size n, and it can't do that if n is greater than the length of p. The implied relationship is that p is indexed by rod size, so that if you want to find the price of a rod of size n, you look at the nth element in p.
How may we model such a relationship in a way that protects the precondition?
An obvious choice, particularly in object-oriented design, is to use a Guard Clause. In the F# code base, it might look like this:
let cut (p : _ array) n = if p.Length <= n then raise (ArgumentOutOfRangeException "n must be less than the length of p") // The rest of the function body...
You might argue that in F# and other functional programming languages, throwing exceptions isn't idiomatic. Instead, you ought to return Result or Option values, here the latter:
let cut (p : _ array) n = if p.Length <= n then None else // The rest of the function body...
To be clear, in most code bases, this is exactly what I would do. What follows is rather exotic, and hardly suitable for all use cases.
Proofs as values #
It's not too hard to model the lower boundary of the n parameter. As is often the case, it turns out that the number must be a natural number. I already covered that in the previous article. It's much harder, however, to model the upper boundary of the value, because it depends on the size of p.
The following is based on the paper Ghosts of Departed Proofs, as well as a helpful Gist also provided by Borar. (The link to the paper is to what I believe is the 'official' page for it, and since it's part of the ACM digital library, it's behind a paywall. Even so, as is the case with most academic papers, it's easy enough to find a PDF of it somewhere else. Not that I endorse content piracy, but it's my impression that academic papers are usually disseminated by the authors themselves.)
The idea is to enable a library to issue a 'proof' about a certain condition. In the example I'm going to use here, the proof is that a certain number is in the valid range for a given list of prices.
We actually can't entirely escape the need for a run-time check, but we do gain two other benefits. The first is that we're now using the type system to communicate a relationship that otherwise would have to be described in written documentation. The second is that once the proof has been issued, there's no need to perform additional run-time checks.
This can help move an API towards a more total, as opposed to partial, definition, which again moves towards what Michael Feathers calls unconditional code. This is particularly useful if the alternative is an API that 'forgets' which run-time guarantees have already been checked. The paper has some examples. I've also recently encountered similar situations when doing Advent of Code 2024. Many days my solution involved immutable maps (like hash tables) that I'd recurse over. In many cases I'd write an algorithm where I with absolute certainty knew that a particular key was in the map (if, for example, I'd just put it there three lines earlier). In such cases, you don't want a total function that returns an option or Maybe value. You want a partial function. Or a type-level guarantee that the value is, indeed, in the map.
For the example in this article, it's overkill, so you may wonder what the point is. On the other hand, a simple example makes it easier to follow what's going on. Hopefully, once you understand the technique, you can extrapolate it to situations where it might be more warranted.
Proof contexts #
The overall idea should look familiar to practitioners of statically-typed functional programming. Instead of plain functions and data structures, we introduce a special 'context' in which we have to run our computations. This is similar to how the IO monad works, or, in fact, most monads. You're not supposed to get the value out of the monad. Rather, you should inject the desired behaviour into the monad.
We find a similar design with existential types, or with the ST monad, on which the ideas in the GDP paper are acknowledged to be based. We even see a mutation-based variation in the article A mutable priority collection, where we may think of the Edit API as a variation of the ST monad, since it allows 'localized' state mutation.
I'll attempt to illustrate it like this:
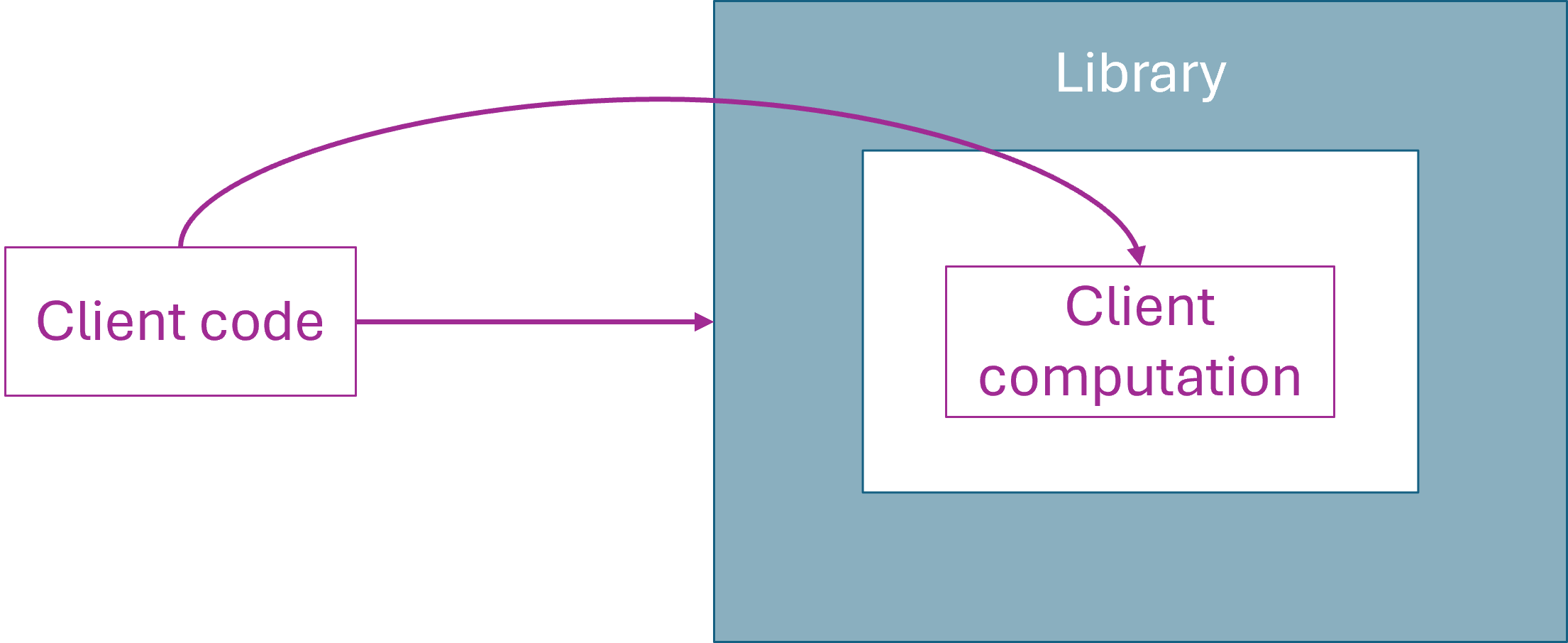
A library offers a set of functions and data structures for immediate use. In addition, it also provides a higher-oder function that enables client code to embed a computation into a special 'sandbox' area where special rules apply. The paper calls such a context a 'name', which it does because it's trying to be as general as possible. As I'm writing this, I find it easier to think of this 'sandbox' as a 'proof context'. It's a context in which proof values exist. Crucially, as we shall see, they don't exist outside of this context.
Size proofs #
In the rod-cutting example, we particularly care about proving that a given number n is within the size of the price list. We do this by representing the proof as a value:
type Size<'a> = private Size of int with member this.Value = let (Size i) = this in i override this.ToString () = let (Size i) = this in string i
Two things are special about this type definition:
- The constructor is
private. - It has a phantom type
'a.
A phantom type is a generic type parameter that has no run-time value. Notice that Size<'a> contains no value of the type 'a. The type only exists at compile-time.
You can think of the type parameter as similar to a security token. The issuer of the proof associates a particular security token to vouch for its validity. Usually, when we talk about security tokens, they do have a run-time representation (typically a byte array) because we need to exchange them with other processes. This is, for example, how claims-based authentication works.

In this case, our concern isn't security. Rather, we wish to communicate and enforce certain relationships. Since we wish to leverage the type system, we use a type as a token.

Since the Size constructor is private, the library controls how it issues proofs, a bit like a claims issuer can sign a claim with its private key.
Okay, but how are Size proofs issued?
Issuing size proofs #
As you'll see later, more than one API may issue Size proofs, but the most fundamental is that you can query a price list for such a proof:
type PriceList<'a> = private PriceList of int list with member this.Length = let (PriceList prices) = this in prices.Length member this.trySize candidate : Size<'a> option = if 0 < candidate && candidate <= this.Length then Some (Size candidate) else None
The trySize member function issues a Some Size<'a> value if the candidate is within the size of the price array. As discussed above, we can't completely avoid a run-time check, but now that we have the proof, we don't need to repeat that run-time check if we wanted to use a particular Size value with the same PriceList.
Notice how immutability is an essential part of this design. If, in the object-oriented manner, we allow a price list to change, we could make it shorter. This could invalidate some proof that we previously issued. Since, however, the price list is immutable, we can trust that once we've checked a size, it remains valid. You can also think of this as a sort of encapsulation, in the sense that once we've assured ourselves that an object, or here rather a value, is valid, it remains valid. Indeed, encapsulation is simpler with immutability.
You probably still have some questions. For instance, how do we ensure that a size proof issued by one price list can't be used against another price list? Imagine that you have two price lists. One has ten prices, the other twenty. You could have the larger one issue a proof that size 17 is valid. What prevents you from using that proof with the smaller price list?
That's the job of that phantom type. Notice how a PriceList<'a> issues a Size<'a> proof. It's the same generic type argument.
Usually, I extol F#'s type inference. I prefer not having to use type annotations unless I have to. When it comes to GDP, however, type annotations are necessary, because we need these phantom types to line up. Without the type annotations, they wouldn't do that.
In the above example, the smaller price list might have the type PriceList<'a> and the larger one the type PriceList<'b>. The smaller would issue proofs of the type Size<'a>, and the larger one proofs of the type Size<'b>. As you'll see, you can't use a Size<'a> where a Size<'b> is required, or vice versa.
You may still wonder how one then creates PriceList<'a> values. After all, that type also has a private constructor.
We'll get back to that later.
Proof-based cut API #
Before we look at how client code may consume APIs based on proofs such as Size<'a>, we should review their expressive power. What does this design enable us to say?
While the first example above, with the Guard Clause alternative, was based on the initial imperative implementation shown in the article Implementing rod-cutting, the rest of the present article builds on the refactored code from Encapsulating rod-cutting.
The first change I need to introduce is to the Cut record type:
type Cut<'a> = { Revenue : int; Size : Size<'a> }
Notice that I've changed the type of the Size property to Size<'a>. This has the implication that Cut<'a> now also has a phantom type, and since client code can't create Size<'a> values, by transitivity it means that neither can client code create Cut<'a> values. These values can only be issued as proofs.
This enables us to change the type definition of the cut function:
let cut (PriceList prices : PriceList<'a>) (Size n : Size<'a>) : Cut<'a> list = // Implementation follows here...
Notice how all the phantom types line up. In order to call the function, client code must supply a Size<'a> value issued by a compatible PriceList<'a> value. Upon a valid call, the function returns a list of Cut<'a> values.
Pay attention to what is being communicated. You may find this strange and impenetrable, but for a reader who understands GDP, much about the contract is communicated through the types. We can see that n relates to prices, because the 'proof token' (the generic type parameter 'a) is the same for both arguments. A reader who understands how Size<'a> proofs are issued will now understand what the preconditions is: The n argument must be valid according to the size of the prices argument.
The type of the cut function also communicates a postcondition: It guarantees that the Size values of each Cut<'a> returned is valid according to the supplied prices. In other words, it means that no defensive coding is necessary. Client code doesn't have to check whether or not the price of each indicated cut can actually be found in prices. The types guarantee that they can.
You may consider the cut function a 'secondary' issuer of Size<'a> proofs, since it returns such values. If you wanted to call cut again with one of those values, you could.
Compared to the previous article, I don't think I changed much else in the cut function, besides the initial function declaration, and the last line of code, but for good measure, here's the entire function:
let cut (PriceList prices : PriceList<'a>) (Size n : Size<'a>) : Cut<'a> list = // Implementation follows here... let p = 0 :: prices |> Array.ofList let findBestCut revenues j = [1..j] |> List.map (fun i -> p[i] + Map.find (j - i) revenues, i) |> List.maxBy fst let aggregate acc j = let revenues = snd acc let q, i = findBestCut revenues j let cuts = fst acc cuts << (cons (q, i)), Map.add revenues.Count q revenues [1..n] |> List.fold aggregate (id, Map.add 0 0 Map.empty) |> fst <| [] // Evaluate Hughes list |> List.map (fun (r, i) -> { Revenue = r; Size = Size i })
The cut function is part of the same module as Size<'a>, so even though the constructor is private, the cut function can still use it.
Thus, the entire proof mechanism is for external use. Internally, the library code may take shortcuts, so it's up to the library author to convince him- or herself that the contract holds. In this case, I'm quite confident that the function only issues valid proofs. After all, I've lifted the algorithm from an acclaimed text book, and this particular implementation is covered by more than 10,000 test cases.
Proof-based solve API #
The solve code hasn't changed, I believe:
let solve prices n = let cuts = cut prices n let rec imp n = if n <= 0 then [] else let idx = n - 1 let s = cuts[idx].Size s :: imp (n - s.Value) imp n.Value
While the code hasn't changed, the type has. In this case, no explicit type annotations are necessary, because the types are already correctly inferred from the use of cut:
solve: prices: PriceList<'a> -> n: Size<'a> -> Size<'a> list
Again, the phantom types line up as desired.
Proof-based revenue calculation #
Although I didn't show it in the previous article, I also included a function to calculate the revenue from a list of cuts. It gets the same treatment as the other functions:
let calculateRevenue (PriceList prices : PriceList<'a>) (cuts : Size<'a> list) = cuts |> List.sumBy (fun s -> prices[s.Value - 1])
Again we see how the GDP-based API communicates a precondition: The cuts must be valid according to the prices; that is, each cut, indicated by its Size property, must be guaranteed to be within the range defined by the price list. This makes the function total; or, unconditional code, as Michael Feathers would put it. The function can't fail at run time.
(I am, once more, deliberately ignoring the entirely independent problem of potential integer overflows.)
While you could repeatedly call PriceList<'a>.trySize to produce a list of cuts, the most natural way to produce such a list of cuts is to first call cut, and then pass its result to calculateRevenue.
The function returns int.
Proof-based printing #
Finally, here's printSolution:
let printSolution p n = solve p n |> List.iter (printfn "%O")
It hasn't changed much since the previous incarnation, but the type is now PriceList<'a> -> Size<'a> -> unit. Again, the precondition is the same as for cut.
Running client code #
How in the world do you write client code against this API? After all, the types all have private constructors, so we can't create any values.
If you trace the code dependencies, you'll notice that PriceList<'a> sits at the heart of the API. If you have a PriceList<'a>, you'd be able to produce the other values, too.
So how do you create a PriceList<'a> value?
You don't. You call the following runPrices function, and give it a PriceListRunner that it'll embed and run in the 'sandbox' illustrated above.
type PriceListRunner<'r> = abstract Run<'a> : PriceList<'a> -> 'r let runPrices pl (ctx : PriceListRunner<'r>) = ctx.Run (PriceList pl)
As the paper describes, the GDP trick hinges on rank-2 polymorphism, and the only way (that I know of) this is supported in F# is on methods. An object is therefore required, and we define the abstract PriceListRunner<'r> class for that purpose.
Client code must implement the abstract class to call the runPrices function. Fortunately, since F# has object expressions, client code might look like this:
[<Fact>] let ``CLRS example`` () = let p = [1; 5; 8; 9; 10; 17; 17; 20; 24; 30] let actual = Rod.runPrices p { new PriceListRunner<_> with member __.Run pl = option { let! n = pl.trySize 10 let cuts = Rod.cut pl n return List.map (fun c -> (c.Revenue, c.Size.Value)) cuts } } [ ( 1, 1) ( 5, 2) ( 8, 3) (10, 2) (13, 2) (17, 6) (18, 1) (22, 2) (25, 3) (30, 10) ] |> Some =! actual
This is an xUnit.net test where actual is produced by runPrices and an object expression that defines the code to run in the proof context. When the Run method runs, it runs with a concrete type that the compiler picked for 'a. This type is only in scope within that method, and can't escape it.
The implementing class is given a PriceList<'a> as an input argument. In this example, it tries to create a size of 10, which succeeds because the price list has ten elements.
Notice that the Run method transforms the cuts to tuples. Why doesn't it return cuts directly?
It can't. It's part of the deal. If I change the last line of Run to return cuts, the code no longer compiles. The compiler error is:
This code is not sufficiently generic. The type variable 'a could not be generalized because it would escape its scope.
Remember I wrote that 'a can't escape the scope of Run? This is enforced by the type system.
Preventing misalignment #
You may already consider it a benefit that this kind of API design uses the type system to communicate pre- and postconditions. Perhaps you also wonder how it prevents errors. As already discussed, if you're dealing with multiple price lists, it shouldn't be possible to use a size proof issued by one, with another. Let's see how that might look. We'll start with a correctly coded unit test:
[<Fact>] let ``Nest two solutions`` () = let p1 = [1; 2; 2] let p2 = [1] let actual = Rod.runPrices p1 { new PriceListRunner<_> with member __.Run pl1 = option { let! n1 = pl1.trySize 3 let cuts1 = Rod.solve pl1 n1 let r = Rod.calculateRevenue pl1 cuts1 let! inner = Rod.runPrices p2 { new PriceListRunner<_> with member __.Run pl2 = option { let! n2 = pl2.trySize 1 let cuts2 = Rod.solve pl2 n2 return Rod.calculateRevenue pl2 cuts2 } } return (r, inner) } } Some (3, 1) =! actual
This code compiles because I haven't mixed up the Size or Cut values. What happens if I 'accidentally' change the 'inner' Rod.solve call to let cuts2 = Rod.solve pl2 n1?
The code doesn't compile:
Type mismatch. Expecting a 'Size<'a>' but given a 'Size<'b>' The type ''a' does not match the type ''b'
This is fortunate, because n1 wouldn't work with pl2. Consider that n1 contains the number 3, which is valid for the larger list pl1, but not the shorter list pl2.
Proofs are issued with a particular generic type argument - the type-level 'token', if you will. It's possible for a library API to explicitly propagate such proofs; you see a hint of that in cut, which not only takes as input a Size<'a> value, but also issues new proofs as a result.
At the same time, this design prevents proofs from being mixed up. Each set of proofs belongs to a particular proof context.
You get the same compiler error if you accidentally mix up some of the other terms.
Conclusion #
One goal in the GDP paper is to introduce a type-safe API design that's also ergonomic. Matt Noonan, the author, defines ergonomic as a design where correct use of the API doesn't place an undue burden on the client developer. The paper's example language is Haskell where rank-2 polymorphism has a low impact on the user.
F# only supports rank-2 polymorphism in method definitions, which makes consuming a GDP API more awkward than in Haskell. The need to create a new type, and the few lines of boilerplate that entails, is a drawback.
Even so, the GDP trick is a nice addition to your functional tool belt. You'll hardly need it every day, but I personally like having some specialized tools lying around together with the everyday ones.
But wait! The reason that F# has support for rank-2 polymorphism through object methods is because C# has that language feature. This must mean that the GDP technique works in C# as well, doesn't it? Indeed it does.
Recawr Sandwich
A pattern variation.
After writing the articles Collecting and handling result values and Short-circuiting an asynchronous traversal, I realized that it might be valuable to describe a more disciplined variation of the Impureim Sandwich pattern.
The book Design Patterns describes each pattern over a number of sections. There's a description of the overall motivation, the structure of the pattern, UML diagrams, examples code, and more. One section discusses various implementation variations. I find it worthwhile, too, to explicitly draw attention to a particular variation of the more overall Impureim Sandwich pattern.
This variation imposes an additional constraint to the general pattern. While this may, at first glance, seem limiting, constraints liberate.

As a specialization, you may consider Recawr Sandwiches as a subset of all Impureim Sandwiches.
Read, calculate, write #
In short, the constraint is that the Sandwich should be organized in the following order:
- Read data. This step is impure.
- Calculate a result from the data. This step is a pure function.
- Write data. This step is impure.
If the sandwich has more than three layers, this order should still be maintained. Once you start writing data to the network, to disk, to a database, or to the user interface, you shouldn't go back to reading in more data.
Naming #
The name Recawr Sandwich is made from the first letters of REad CAlculate WRite. It's pronounced recover sandwich.
When the idea of naming this variation originally came to me, I first thought of the name read/write sandwich, but then I thought that the most important ingredient, the pure function, was missing. I've considered some other variations, such as read, pure, write sandwich or input, referential transparency, output sandwich, but none of them quite gets the point across, I think, in the same way as read, calculate, write.
Precipitating example #
To be clear, I've been applying the Recawr Sandwich pattern for years, but it sometimes takes a counter-example before you realize that some implicit, tacit knowledge should be made explicit. This happened to me as I was discussing this implementation of Impureim Sandwich:
// Impure IEnumerable<OneOf<ShoppingListItem, NotFound<ShoppingListItem>, Error>> results = await itemsToUpdate.Traverse(item => UpdateItem(item, dbContext)); // Pure var result = results.Aggregate( new BulkUpdateResult([], [], []), (state, result) => result.Match( storedItem => state.Store(storedItem), notFound => state.Fail(notFound.Item), error => state.Error(error))); // Impure await dbContext.SaveChangesAsync(); return new OkResult(result);
Notice that the top impure step traverses a collection of items to apply each to an action called UpdateItem. As I discussed in the article, I don't actually know what UpdateItem does, but the name strongly suggests that it updates a particular database row. Even if the actual write doesn't happen until SaveChangesAsync is called, this still seems off.
To be honest, I didn't realize this until I started thinking about how I'd go about solving the implied problem, if I had to do it from scratch. Because I probably wouldn't do it like that at all.
It strikes me that doing the update 'too early' makes the code more complicated than it has to be.
What would a Recawr Sandwich look like?
Recawr example #
Perhaps one could instead start by querying the database about which items are actually in it, then prepare the result, and finally make the update.
// Read var existing = await FilterExisting(itemsToUpdate, dbContext); // Calculate var result = new BulkUpdateResult([.. existing], [.. itemsToUpdate.Except(existing)], []); // Write var results = await existing.Traverse(item => UpdateItem(item, dbContext)); await dbContext.SaveChangesAsync(); return new OkResult(result);
To be honest, this variation has different behaviour when Error values occur, but then again, I wasn't entirely sure what was even the purpose of the error value. If it's to model errors that client code can't recover from, throw an exception instead.
In any case, the example is typical of many I/O-heavy operations, which veer dangerously close to the degenerate. There really isn't a lot of logic required, so one may reasonably ask whether the example is useful. It was, however, the example that got me thinking about giving the Recawr Sandwich an explicit name.
Other examples #
All the examples in the original Impureim Sandwich article are actually Recawr Sandwiches. Other articles with clear Recawr Sandwich examples are:
- Picture archivist in Haskell
- Picture archivist in F#
- The Command Handler contravariant functor
- A restaurant sandwich
In other words, I'm just retroactively giving these examples a more specific label.
What's an example of an Impureim Sandwich which is not a Recawr Sandwich? Ironically, the first example in this article.
Conclusion #
A Recawr Sandwich is a specialization of the slightly more general Impureim Sandwich pattern. It specializes by assigning roles to the two impure layers of the sandwich. In the first, the code reads data. In the second impure layer, it writes data. In between, it performs referentially transparent calculations.
While more constraining, this specialization offers a good rule of thumb. Most well-designed sandwiches follow this template.
Encapsulating rod-cutting
Focusing on usage over implementation.
This article is a part of a small article series about implementation and usage mindsets. The hypothesis is that programmers who approach a problem with an implementation mindset may gravitate toward dynamically typed languages, whereas developers concerned with long-term maintenance and sustainability of a code base may be more inclined toward statically typed languages. This could be wrong, and is almost certainly too simplistic, but is still, I hope, worth thinking about. In the previous article you saw examples of an implementation-centric approach to problem-solving. In this article, I'll discuss what a usage-first perspective entails.
A usage perspective indicates that you're first and foremost concerned with how useful a programming interface is. It's what you do when you take advantage of test-driven development (TDD). First, you write a test, which furnishes an example of what a usage scenario looks like. Only then do you figure out how to implement the desired API.
In this article I didn't use TDD since I already had a particular implementation. Even so, while I didn't mention it in the previous article, I did add tests to verify that the code works as intended. In fact, because I wrote a few Hedgehog properties, I have more than 10.000 test cases covering my implementation.
I bring this up because TDD is only one way to focus on sustainability and encapsulation. It's the most scientific methodology that I know of, but you can employ more ad-hoc, ex-post analysis processes. I'll do that here.
Imperative origin #
In the previous article you saw how the Extended-Bottom-Up-Cut-Rod pseudocode was translated to this F# function:
let cut (p : _ array) n = let r = Array.zeroCreate (n + 1) let s = Array.zeroCreate (n + 1) r[0] <- 0 for j = 1 to n do let mutable q = Int32.MinValue for i = 1 to j do if q < p[i] + r[j - i] then q <- p[i] + r[j - i] s[j] <- i r[j] <- q r, s
In case anyone is wondering: This is a bona-fide pure function, even if the implementation is as imperative as can be. Given the same input, cut always returns the same output, and there are no side effects. We may wish to implement the function in a more idiomatic way, but that's not our first concern. My first concern, at least, is to make sure that preconditions, invariants, and postconditions are properly communicated.
The same goal applies to the printSolution action, also repeated here for your convenience.
let printSolution p n = let _, s = cut p n let mutable n = n while n > 0 do printfn "%i" s[n] n <- n - s[n]
Not that I'm not interested in more idiomatic implementations, but after all, they're by definition just implementation details, so first, I'll discuss encapsulation. Or, if you will, the usage perspective.
Names and types #
Based on the above two code snippets, we're given two artefacts: cut and printSolution. Since F# is a statically typed language, each operation also has a type.
The type of cut is int array -> int -> int array * int array. If you're not super-comfortable with F# type signatures, this means that cut is a function that takes an integer array and an integer as inputs, and returns a tuple as output. The output tuple is a pair; that is, it contains two elements, and in this particular case, both elements have the same type: They are both integer arrays.
Likewise, the type of printSolution is int array -> int -> unit, which again indicates that inputs must be an integer array and an integer. In this case the output is unit, which, in a sense, corresponds to void in many C-based languages.
Both operations belong to a module called Rod, so their slightly longer, more formal names are Rod.cut and Rod.printSolution. Even so, good names are only skin-deep, and I'm not even convinced that these are particularly good names. To be fair to myself, I adopted the names from the pseudocode from Introduction to Algorithms. Had I been freer to name function and design APIs, I might have chosen different names. As it is, currently, there's no documentation, so the types are the only source of additional information.
Can we infer proper usage from these types? Do they sufficiently well communicate preconditions, invariants, and postconditions? In other words, do the types satisfactorily indicate the contract of each operation? Do the functions exhibit good encapsulation?
We may start with the cut function. It takes as inputs an integer array and an integer. Are empty arrays allowed? Are all integers valid, or perhaps only natural numbers? What about zeroes? Are duplicates allowed? Does the array need to be sorted? Is there a relationship between the array and the integer? Can the single integer parameter be negative?
And what about the return value? Are the two integer arrays related in any way? Can one be empty, but the other large? Can they both be empty? May negative numbers or zeroes be present?
Similar questions apply to the printSolution action.
Not all such questions can be answered by types, but since we already have a type system at our disposal, we might as well use it to address those questions that are easily modelled.
Encapsulating the relationship between price array and rod length #
The first question I decided to answer was this: Is there a relationship between the array and the integer?
The array, you may recall, is an array of prices. The integer is the length of the rod to cut up.
A relationship clearly exists. The length of the rod must not exceed the length of the array. If it does, cut throws an IndexOutOfRangeException. We can't calculate the optimal cuts if we lack price information.
Likewise, we can already infer that the length must be a non-negative number.
While we could choose to enforce this relationship with Guard Clauses, we may also consider a simpler API. Let the function infer the rod length from the array length.
let cut (p : _ array) = let n = p.Length - 1 let r = Array.zeroCreate (n + 1) let s = Array.zeroCreate (n + 1) r[0] <- 0 for j = 1 to n do let mutable q = Int32.MinValue for i = 1 to j do if q < p[i] + r[j - i] then q <- p[i] + r[j - i] s[j] <- i r[j] <- q r, s
You may argue that this API is more implicit, which we generally don't like. The implication is that the rod length is determined by the array length. If you have a (one-indexed) price array of length 10, then how do you calculate the optimal cuts for a rod of length 7?
By shortening the price array:
> let p = [|0; 1; 5; 8; 9; 10; 17; 17; 20; 24; 30|];; val p: int array = [|0; 1; 5; 8; 9; 10; 17; 17; 20; 24; 30|] > cut (p |> Array.take (7 + 1));; val it: int array * int array = ([|0; 1; 5; 8; 10; 13; 17; 18|], [|0; 1; 2; 3; 2; 2; 6; 1|])
This is clearly still sub-optimal. Notice, for example, how you need to add 1 to 7 in order to deal with the prefixed 0. On the other hand, we're not done with the redesign, so it may be worth pursuing this course a little further.
(To be honest, while this is the direction I ultimately choose, I'm not blind to the disadvantages of this implicit design. It makes it less clear to a client developer how to indicate a rod length. An alternative design would keep the price array and the rod length as two separate parameters, but then introduce a Guard Clause to check that the rod length doesn't exceed the length of the price array. Outside of dependent types I can't think of a way to model such a relationship between two values, and I admit to having no practical experience with dependent types. All this said, however, it's also possible that I'm missing an obvious design alternative. If you can think of a way to model this relationship in a non-predicative way, please write a comment.)
I gave the printSolution the same treatment, after first having extracted a solve function in order to separate decisions from effects.
let solve p = let _, s = cut p let l = ResizeArray () let mutable n = p.Length - 1 while n > 0 do l.Add s[n] n <- n - s[n] l |> List.ofSeq let printSolution p = solve p |> List.iter (printfn "%i")
The implementation of the solve function is still imperative, but if you view it as a black box, it's referentially transparent. We'll get back to the implementation later.
Returning a list of cuts #
Let's return to all the questions I enumerated above, particularly the questions about the return value. Are the two integer arrays related?
Indeed they are! In fact, they have the same length.
As explained in the previous article, in the original pseudocode, the r array is supposed to be zero-indexed, but non-empty and containing 0 as the first element. The s array is supposed to be one-indexed, and be exactly one element shorter than the r array. In practice, in all three implementations shown in that article, I made both arrays zero-indexed, non-empty, and of the exact same length. This is also true for the F# implementation.
We can communicate this relationship much better to client developers by changing the return type of the cut function. Currently, the return type is int array * int array, indicating a pair of arrays. Instead, we can change the return type to an array of pairs, thereby indicating that the values are related two-and-two.
That would be a decent change, but we can further improve the API. A pair of integers are still implicit, because it isn't clear which integer represents the revenue and which one represents the size. Instead, we introduce a custom type with clear labels:
type Cut = { Revenue : int; Size : int }
Then we change the cut function to return a collection of Cut values:
let cut (p : _ array) = let n = p.Length - 1 let r = Array.zeroCreate (n + 1) let s = Array.zeroCreate (n + 1) r[0] <- 0 for j = 1 to n do let mutable q = Int32.MinValue for i = 1 to j do if q < p[i] + r[j - i] then q <- p[i] + r[j - i] s[j] <- i r[j] <- q let result = ResizeArray () for i = 0 to n do result.Add { Revenue = r[i]; Size = s[i] } result |> List.ofSeq
The type of cut is now int array -> Cut list. Notice that I decided to return a linked list rather than an array. This is mostly because I consider linked lists to be more idiomatic than arrays in a context of functional programming (FP), but to be honest, I'm not sure that it makes much difference as a return value.
In any case, you'll observe that the implementation is still imperative. The main topic of this article is how to give an API good encapsulation, so I treat the actual code as an implementation detail. It's not the most important thing.
Linked list input #
Although I wrote that I'm not sure it makes much difference whether cut returns an array or a list, it does matter when it comes to input values. Currently, cut takes an int array as input.
As the implementation so amply demonstrates, F# arrays are mutable; you can mutate the cells of an array. A client developer may worry, then, whether cut modifies the input array.
From the implementation code we know that it doesn't, but encapsulation is all about sparing client developers the burden of having to read the implementation. Rather, an API should communicate its contract in as succinct a way as possible, either via documentation or the type system.
In this case, we can use the type system to communicate this postcondition. Changing the input type to a linked list effectively communicates to all users of the API that cut doesn't mutate the input. This is because F# linked lists are truly immutable.
let cut prices = let p = prices |> Array.ofList let n = p.Length - 1 let r = Array.zeroCreate (n + 1) let s = Array.zeroCreate (n + 1) r[0] <- 0 for j = 1 to n do let mutable q = Int32.MinValue for i = 1 to j do if q < p[i] + r[j - i] then q <- p[i] + r[j - i] s[j] <- i r[j] <- q let result = ResizeArray () for i = 0 to n do result.Add { Revenue = r[i]; Size = s[i] } result |> List.ofSeq
The type of the cut function is now int list -> Cut list, which informs client developers of an invariant. You can trust that cut will not change the input arguments.
Natural numbers #
You've probably gotten the point by now, so let's move a bit quicker. There are still issues that we'd like to document. Perhaps the worst part of the current API is that client code is required to supply a prices list where the first element must be zero. That's a very specific requirement. It's easy to forget, and if you do, the cut function just silently fails. It doesn't throw an exception; it just gives you a wrong answer.
We may choose to add a Guard Clause, but why are we even putting that responsibility on the client developer? Why can't the cut function add that prefix itself? It can, and it turns out that once you do that, and also remove the initial zero element from the output, you're now working with natural numbers.
First, add a NaturalNumber wrapper of integers:
type NaturalNumber = private NaturalNumber of int with member this.Value = let (NaturalNumber i) = this in i static member tryCreate candidate = if candidate < 1 then None else Some <| NaturalNumber candidate override this.ToString () = let (NaturalNumber i) = this in string i
Since the case constructor is private, external code can only try to create values. Once you have a NaturalNumber value, you know that it's valid, but creation requires a run-time check. In other words, this is what Hillel Wayne calls predicative data.
Armed with this new type, however, we can now strengthen the definition of the Cut record type:
type Cut = { Revenue : int; Size : NaturalNumber } with static member tryCreate revenue size = NaturalNumber.tryCreate size |> Option.map (fun size -> { Revenue = revenue; Size = size })
The Revenue may still be any integer, because it turns out that the algorithm also works with negative prices. (For a book that's very meticulous in its analysis of algorithms, CLRS is surprisingly silent on this topic. Thorough testing with Hedgehog, however, indicates that this is so.) On the other hand, the Size of the Cut must be a NaturalNumber. Since, again, we don't have any constructive way (outside of using refinement types) of modelling this requirement, we also supply a tryCreate function.
This enables us to define the cut function like this:
let cut prices = let p = prices |> List.append [0] |> Array.ofList let n = p.Length - 1 let r = Array.zeroCreate (n + 1) let s = Array.zeroCreate (n + 1) r[0] <- 0 for j = 1 to n do let mutable q = Int32.MinValue for i = 1 to j do if q < p[i] + r[j - i] then q <- p[i] + r[j - i] s[j] <- i r[j] <- q let result = ResizeArray () for i = 1 to n do Cut.tryCreate r[i] s[i] |> Option.iter result.Add result |> List.ofSeq
It still has the type int list -> Cut list, but the Cut type is now more restrictively designed. In other words, we've provided a more conservative definition of what we return, in keeping with Postel's law.
Furthermore, notice that the first line prepends 0 to the p array, so that the client developer doesn't have to do that. Likewise, when returning the result, the for loop goes from 1 to n, which means that it omits the first zero cut.
These changes ripple through and also improves encapsulation of the solve function:
let solve prices = let cuts = cut prices let l = ResizeArray () let mutable n = prices.Length while n > 0 do let idx = n - 1 let s = cuts.[idx].Size l.Add s n <- n - s.Value l |> List.ofSeq
The type of solve is now int list -> NaturalNumber list.
This is about as strong as I can think of making the API using F#'s type system. A type like int list -> NaturalNumber list tells you something about what you're allowed to do, what you're expected to do, and what you can expect in return. You can provide (almost) any list of integers, both positive, zero, or negative. You may also give an empty list. If we had wanted to prevent that, we could have used a NonEmpty list, as seen (among other places) in the article Conservative codomain conjecture.
Okay, to be perfectly honest, there's one more change that might be in order, but this is where I ran out of steam. One remaining precondition that I haven't yet discussed is that the input list must not contain 'too big' numbers. The problem is that the algorithm adds numbers together, and since 32-bit integers are bounded, you could run into overflow situations. Ask me how I know.
Changing the types to use 64-bit integers doesn't solve that problem (it only moves the boundary of where overflow happens), but consistently changing the API to work with BigInteger values might. To be honest, I haven't tried.
Functional programming #
From an encapsulation perspective, we're done now. By using the type system, we've emphasized how to use the API, rather than how it's implemented. Along the way, we even hid away some warts that came with the implementation. If I wanted to take this further, I would seriously consider making the cut function a private helper function, because it doesn't really return a solution. It only returns an intermediary value that makes it easier for the solve function to return the actual solution.
If you're even just a little bit familiar with F# or functional programming, you may have found it painful to read this far. All that imperative code. My eyes! For the love of God, please rewrite the implementation with proper FP idioms and patterns.
Well, the point of the whole article is that the implementation doesn't really matter. It's how client code may use the API that's important.
That is, of course, until you have to go and change the implementation code. In any case, as a little consolation prize for those brave FP readers who've made it all this way, here follows more functional implementations of the functions.
The NaturalNumber and Cut types haven't changed, so the first change comes with the cut function:
let private cons x xs = x :: xs let cut prices = let p = 0 :: prices |> Array.ofList let n = p.Length - 1 let findBestCut revenues j = [1..j] |> List.map (fun i -> p[i] + Map.find (j - i) revenues, i) |> List.maxBy fst let aggregate acc j = let revenues = snd acc let q, i = findBestCut revenues j let cuts = fst acc cuts << (cons (q, i)), Map.add revenues.Count q revenues [1..n] |> List.fold aggregate (id, Map.add 0 0 Map.empty) |> fst <| [] // Evaluate Hughes list |> List.choose (fun (r, i) -> Cut.tryCreate r i)
Even here, however, some implementation choices are dubious at best. For instance, I decided to use a Hughes list or difference list (see Tail Recurse for a detailed explanation of how this works in F#) without measuring whether or not it was better than just using normal list consing followed by List.rev (which is, in fact, often faster). That's one of the advantages of writing code for articles; such things don't really matter that much in that context.
Another choice that may leave you scratching your head is that I decided to model the revenues as a map (that is, an immutable dictionary) rather than an array. I did this because I was concerned that with the move towards immutable code, I'd have n reallocations of arrays. Perhaps, I thought, adding incrementally to a Map structure would be more efficient.
But really, all of that is just wanking, because I haven't measured.
The FP-style implementation of solve is, I believe, less controversial:
let solve prices = let cuts = cut prices let rec imp n = if n <= 0 then [] else let idx = n - 1 let s = cuts[idx].Size s :: imp (n - s.Value) imp prices.Length
This is a fairly standard implementation using a local recursive helper function.
Both cut and solve have the types previously reported. In other words, this final refactoring to functional implementations didn't change their types.
Conclusion #
This article goes through a series of code improvements to illustrate how a static type system can make it easier to use an API. Use it correctly, that is.
There's a common misconception about ease of use that it implies typing fewer characters, or getting instant gratification. That's not my position. Typing is not a bottleneck, and in any case, not much is gained if you make it easier for client developers to get the wrong answers from your API.
Static types gives you a consistent vocabulary you can use to communicate an API's contract to client developers. What must client code do in order to make a valid method or function call? What guarantees can client code rely on? Encapsulation, in other words.
P.S. 2025-01-20:
For a type-level technique for modelling the relationship between rod size and price list, see Modelling data relationships with F# types.
Pytest is fast
One major attraction of Python. A recent realization.
Ever since I became aware of the distinction between statically and dynamically typed languages, I've struggled to understand the attraction of dynamically typed languages. As regular readers may have noticed, this is a bias that doesn't sit well with me. Clearly, there are advantages to dynamic languages that I fail to notice. Is it a question of mindset? Or is it a combination of several small advantages?
In this article, I'll discuss another potential benefit of at least one dynamically typed language, Python.
Fast feedback #
Rapid feedback is a cornerstone of modern software engineering. I've always considered the feedback from the compiler an important mechanism, but I've recently begun to realize that it comes with a price. While a good type system keeps you honest, compilation takes time, too.
Since I've been so entrenched in the camp of statically typed languages (C#, F#, Haskell), I've tended to regard compilation as a mandatory step. And since the compiler needs to run anyway, you might as well take advantage of it. Use the type system to make illegal states unrepresentable, and all that.
Even so, I've noticed that compilation time isn't a fixed size. This observation surely borders on the banal, but with sufficient cognitive bias, it can, apparently, take years to come to even such a trivial conclusion. After initial years with various programming languages, my formative years as a programmer were spent with C#. As it turns out, the C# compiler is relatively fast.
This is probably a combination of factors. Since C# is a one of the most popular languages, it has a big and skilled engineering team, and it's my impression that much effort goes into making it as fast and efficient as possible.
I also speculate that, since the C# type system isn't as powerful as F#'s or Haskell's, there's simply work that it can't do. When you can't expression certain constraints or relationships with the type system, the compiler can't check them, either.
That said, the C# compiler seems to have become slower over the years. This could be a consequence of all the extra language features that accumulate.
The F# compiler, in comparison, has always taken longer than the C# compiler. Again, this may be due to a combination of a smaller engineering team and that it actually can check more things at compile time, since the type system is more expressive.
This, at least, seems to fit with the observation that the Haskell compiler is even slower than F#. The language is incredibly expressive. There's a lot of constraints and relationships that you can model with the type system. Clearly, the compiler has to perform extra work to check that your types line up.
You're often left with the impression that if it compiles, it works. The drawback is that getting Haskell code to compile may be a non-trivial undertaking.
One thing is that you'll have to wait for the compiler. Another is that if you practice test-driven development (TDD), you'll have to compile the test code, too. Only once the tests are compiled can you run them. And TDD test suites should run in 10 seconds or less.
Skipping compilation with pytest #
A few years ago I had to learn a bit of Python, so I decided to try Advent of Code 2022 in Python. As the puzzles got harder, I added unit tests with pytest. When I ran them, I was taken aback at how fast they ran.
There's no compilation step, so the test suite runs immediately. Obviously, if you've made a mistake that a compiler would have caught, the test fails, but if the code makes sense to the interpreter, it just runs.
For various reasons, I ran out of steam, as one does with Advent of Code, but I managed to write a good little test suite. Until day 17, it ran in 0.15-0.20 seconds on my little laptop. To be honest, though, once I added tests for day 17, feedback time jumped to just under two seconds. This is clearly because I'd written some inefficient code for my System Under Test.
I can't really blame a test framework for being slow, when it's really my own code that slows it down.
A counter-argument is that a compiled language is much faster than an interpreted one. Thus, one might think that a faster language would counter poor implementations. Not so.
TDD with Haskell #
As I've already outlined, the Haskell compiler takes more time than C#, and obviously it takes more time than a language that isn't compiled at all. On the other hand, Haskell compiles to native machine code. My experience with it is that once you've compiled your program, it's fast.
In order to compare the two styles, I decided to record compilation and test times while doing Advent of Code 2024 in Haskell. I set up a Haskell code base with Stack and HUnit, as I usually do. As I worked through the puzzles, I'd be adding and running tests. Every time I recorded the time it took, using the time command to measure the time it took for stack test to run.
I've plotted the observations in this chart:
The chart shows more than a thousand observations, with the first to the left, and the latest to the right. The times recorded are the entire time it took from I started a test run until I had an answer. For this, I used the time command's real time measurement, rather than user or sys time. What matters is the feedback time; not the CPU time.
Each measurement is in seconds. The dashed orange line indicates the linear trend.
It's not the first time I've written Haskell code, so I knew what to expect. While you get the occasional fast turnaround time, it easily takes around ten seconds to compile even an empty code base. It seems that there's a constant overhead of that size. While there's an upward trend line as I added more and more code, and more tests, actually running the tests takes almost no time. The initial 'average' feedback time was around eight seconds, and 1100 observations later, the trends sits around 11.5 seconds. At this time, I had more than 200 test cases.
You may also notice that the observations vary quite a bit. You occasionally see sub-second times, but also turnaround times over thirty seconds. There's an explanation for both.
The sub-second times usually happen if I run the test suite twice without changing any code. In that case, the Haskell Stack correctly skips recompiling the code and instead just reruns the tests. This only highlights that I'm not waiting for the tests to execute. The tests are fast. It's the compiler that causes over 90% of the delay.
(Why would I rerun a test suite without changing any code? This mostly happens when I take a break from programming, or if I get distracted by another task. In such cases, when I return to the code, I usually run the test suite in order to remind myself of the state in which I left it. Sometimes, it turns out, I'd left the code in a state were the last thing I did was to run all tests.)
The other extremes have a different explanation.
IDE woes #
Why do I have to suffer through those turnaround times over twenty seconds? A few times over thirty?
The short answer is that these represent complete rebuilds. Most of these are caused by problems with the IDE. For Haskell development, I use Visual Studio Code with the Haskell extension.
Perhaps it's only my setup that's messed up, but whenever I change a function in the System Under Test (SUT), I can. not. make. VS Code pick up that the API changed. Even if I correct my tests so that they still compile and run successfully from the command line, VS Code will keep insisting that the code is wrong.
This is, of course, annoying. One of the major selling points of statically type languages is that a good IDE can tell you if you made mistakes. Well, if it operates on an outdated view of what the SUT looks like, this no longer works.
I've tried restarting the Haskell Language Server, but that doesn't work. The only thing that works, as far as I've been able to discover, is to close VS Code, delete .stack-work, recompile, and reopen VS Code. Yes, that takes a minute or two, so not something I like doing too often.
Deleting .stack-work does trigger a full rebuild, which is why we see those long build times.
Striking a good balance #
What bothers me about dynamic languages is that I find discoverability and encapsulation so hard. I can't just look at the type of an operation and deduce what inputs it might take, or what the output might look like.
To be honest, if you give me a plain text file with F# or Haskell, I can't do that either. A static type system doesn't magically surface that kind of information. Instead, you may rely on an IDE to provide such information at your fingertips. The Haskell extension, for example, gives you a little automatic type annotation above your functions, as discussed in the article Pendulum swing: no Haskell type annotation by default, and shown in a figure reprinted here for your convenience:

If this is to work well, this information must be immediate and responsive. On my system it isn't.
It may, again, be that there's some problem with my particular tool chain setup. Or perhaps a four-year-old Lenovo X1 Carbon is just too puny a machine to effectively run such a tool.
On the other hand, I don't have similar issues with C# in Visual Studio (not VS Code). When I make changes, the IDE quickly responds and tells me if I've made a mistake. To be honest, even here, I feel that it was faster and more responsive a decade ago, but compared to Haskell programming, the feedback I get with C# is close to immediate.
My experience with F# is somewhere in between. Visual Studio is quicker to pick up changes in F# code than VS Code is to reflect changes in Haskell, but it's not as fast as C#.
With Python, what little IDE integration is available is usually not trustworthy. Essentially, when suggesting callable operations, the IDE is mostly guessing, based on what it's already seen.
But, good Lord! The tests run fast.
Conclusion #
My recent experiences with both Haskell and Python programming is giving me a better understanding of the balances and trade-offs involved with picking a language. While I still favour statically typed languages, I'm beginning to see some attractive qualities on the other side.
Particularly, if you buy the argument that TDD suites should run in 10 seconds or less, this effectively means that I can't do TDD in Haskell. Not with the hardware I'm running. Python, on the other hand, seems eminently well-suited for TDD.
That doesn't sit too well with me, but on the other hand, I'm glad. I've learned about a benefit of a dynamically typed language. While you may consider all of this ordinary and trite, it feels like a small breakthrough to me. I've been trying hard to see past my own limitations, and it finally feels as though I've found a few chinks in the armour of my biases.
I'll keep pushing those envelopes to see what else I may learn.
Implementing rod-cutting
From pseudocode to implementation in three languages.
This article picks up where Implementation and usage mindsets left off, examining how easy it is to implement an algorithm in three different programming languages.
As an example, I'll use the bottom-up rod-cutting algorithm from Introduction to Algorithms.
Rod-cutting #
The problem is simple:
"Serling Enterprises buys long steel rods and cuts them into shorter rods, which it then sells. Each cut is free. The management of Serling Enterprises wants to know the best way to cut up the rods."
You're given an array of prices, or rather revenues, that each size is worth. The example from the book is given as a table:
| length i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| price pi | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
Notice that while this implies an array like [1, 5, 8, 9, 10, 17, 17, 20, 24, 30], the array is understood to be one-indexed, as is the most common case in the book. Most languages, including all three languages in this article, have zero-indexed arrays, but it turns out that we can get around the issue by adding a leading zero to the array: [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30].
Thus, given that price array, the best you can do with a rod of length 10 is to leave it uncut, yielding a revenue of 30.
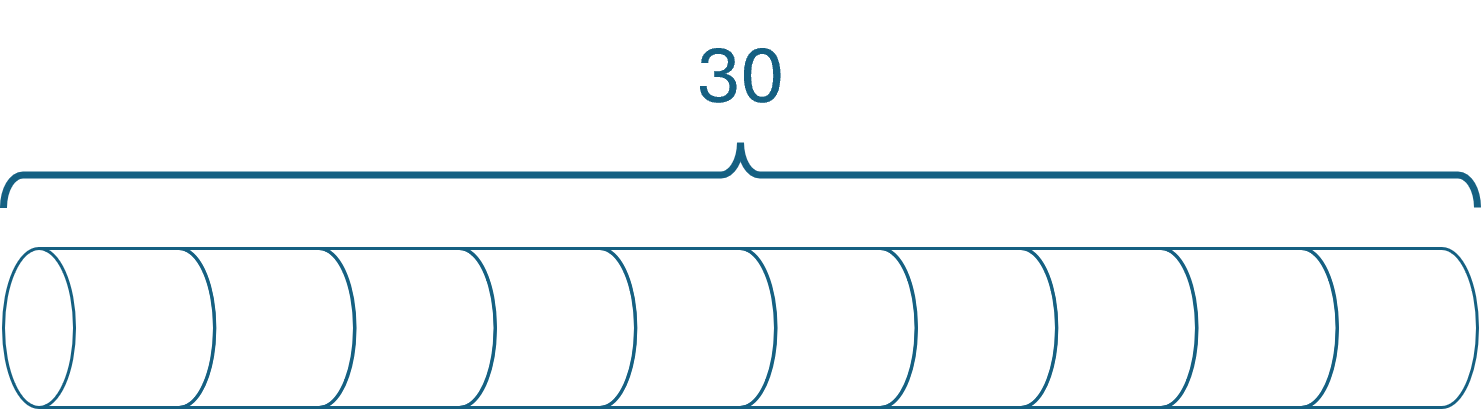
On the other hand, if you have a rod of length 7, you can cut it into two rods of lengths 1 and 6.
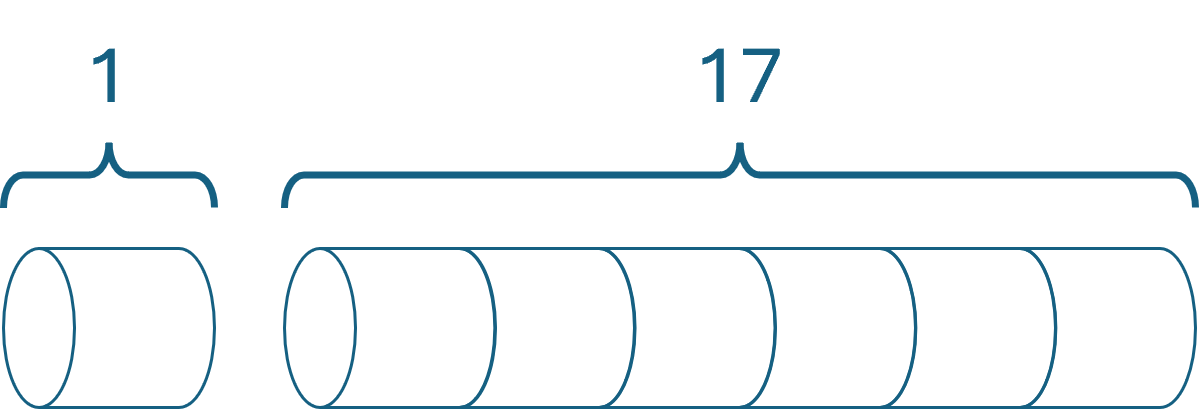
Another solution for a rod of length 7 is to cut it into three rods of sizes 2, 2, and 3. Both solutions yield a total revenue of 18. Thus, while more than one optimal solution exists, the algorithm given here only identifies one of them.
Extended-Bottom-Up-Cut-Rod(p, n) 1 let r[0:n] and s[1:n] be new arrays 2 r[0] = 0 3 for j = 1 to n // for increasing rod length j 4 q = -∞ 5 for i = 1 to j // i is the position of the first cut 6 if q < p[i] + r[j - i] 7 q = p[i] + r[j - i] 8 s[j] = i // best cut location so far for length j 9 r[j] = q // remember the solution value for length j 10 return r and s
Which programming language is this? It's no particular language, but rather pseudocode.
The reason that the function is called Extended-Bottom-Up-Cut-Rod is that the book pedagogically goes through a few other algorithms before arriving at this one. Going forward, I don't intend to keep that rather verbose name, but instead just call the function cut_rod, cutRod, or Rod.cut.
The p parameter is a one-indexed price (or revenue) array, as explained above, and n is a rod size (e.g. 10 or 7, reflecting the above examples).
Given the above price array and n = 10, the algorithm returns two arrays, r for maximum possible revenue for a given cut, and s for the size of the maximizing cut.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| r[i] | 0 | 1 | 5 | 8 | 10 | 13 | 17 | 18 | 22 | 25 | 30 |
| s[i] | 1 | 2 | 3 | 2 | 2 | 6 | 1 | 2 | 3 | 10 |
Such output doesn't really give a solution, but rather the raw data to find a solution. For example, for n = 10 (= i), you consult the table for (one-indexed) index 10, and see that you can get the revenue 30 from making a cut at position 10 (which effectively means no cut). For n = 7, you consult the table for index 7 and observe that you can get the total revenue 18 by making a cut at position 1. This leaves you with two rods, and you again consult the table. For n = 1, you can get the revenue 1 by making a cut at position 1; i.e. no further cut. For n = 7 - 1 = 6 you consult the table and observe that you can get the revenue 17 by making a cut at position 6, again indicating that no further cut is necessary.
Another procedure prints the solution, using the above process:
Print-Cut-Rod-Solution(p, n) 1 (r, s) = Extended-Bottom-Up-Cut-Rod(p, n) 2 while n > 0 3 print s[n] // cut location for length n 4 n = n - s[n] // length of the remainder of the rod
Again, the procedure is given as pseudocode.
How easy is it translate this algorithm into code in a real programming language? Not surprisingly, this depends on the language.
Translation to Python #
The hypothesis of the previous article is that dynamically typed languages may be more suited for implementation tasks. The dynamically typed language that I know best is Python, so let's try that.
def cut_rod(p, n): r = [0] * (n + 1) s = [0] * (n + 1) r[0] = 0 for j in range(1, n + 1): q = float('-inf') for i in range(1, j + 1): if q < p[i] + r[j - i]: q = p[i] + r[j - i] s[j] = i r[j] = q return r, s
That does, indeed, turn out to be straightforward. I had to figure out the syntax for initializing arrays, and how to represent negative infinity, but a combination of GitHub Copilot and a few web searches quickly cleared that up.
The same is true for the Print-Cut-Rod-Solution procedure.
def print_cut_rod_solution(p, n): r, s = cut_rod(p, n) while n > 0: print(s[n]) n = n - s[n]
Apart from minor syntactical differences, the pseudocode translates directly to Python.
So far, the hypothesis seems to hold. This particular dynamically typed language, at least, easily implements that particular algorithm. If we must speculate about underlying reasons, we may argue that a dynamically typed language is low on ceremony. You don't have to get side-tracked by declaring types of parameters, variables, or return values.
That, at least, is a common complaint about statically typed languages that I hear when I discuss with lovers of dynamically typed languages.
Let us, then, try to implement the rod-cutting algorithm in a statically typed language.
Translation to Java #
Together with other C-based languages, Java is infamous for requiring a high amount of ceremony to get anything done. How easy is it to translate the rod-cutting pseudocode to Java? Not surprisingly, it turns out that one has to jump through a few more hoops.
First, of course, one has to set up a code base and choose a build system. I'm not well-versed in Java development, but here I (more or less) arbitrarily chose gradle. When you're new to an ecosystem, this can be a significant barrier, but I know from decades of C# programming that tooling alleviates much of that pain. Still, a single .py file this isn't.
Apart from that, the biggest hurdle turned out to be that, as far as I can tell, Java doesn't have native tuple support. Thus, in order to return two arrays, I would have to either pick a reusable package that implements tuples, or define a custom class for that purpose. Object-oriented programmers often argue that tuples represent poor design, since a tuple doesn't really communicate the role or intent of each element. Given that the rod-cutting algorithm returns two integer arrays, I'd be inclined to agree. You can't even tell them apart based on their types. For that reason, I chose to define a class to hold the result of the algorithm.
public class RodCuttingSolution { private int[] revenues; private int[] sizes; public RodCuttingSolution(int[] revenues, int[] sizes) { this.revenues = revenues; this.sizes = sizes; } public int[] getRevenues() { return revenues; } public int[] getSizes() { return sizes; } }
Armed with this return type, the rest of the translation went smoothly.
public static RodCuttingSolution cutRod(int[] p, int n) { var r = new int[n + 1]; var s = new int[n + 1]; r[0] = 0; for (int j = 1; j <= n; j++) { var q = Integer.MIN_VALUE; for (int i = 1; i <= j; i++) { if (q < p[i] + r[j - i]) { q = p[i] + r[j - i]; s[j] = i; } } r[j] = q; } return new RodCuttingSolution(r, s); }
Granted, there's a bit more ceremony involved compared to the Python code, since one must declare the types of both input parameters and method return type. You also have to declare the type of the arrays when initializing them, and you could argue that the for loop syntax is more complicated than Python's for ... in range ... syntax. One may also complain that all the brackets and parentheses makes it harder to read the code.
While I'm used to such C-like code, I'm not immune to such criticism. I actually do find the Python code more readable.
Translating the Print-Cut-Rod-Solution pseudocode is a bit easier:
public static void printCutRodSolution(int[] p, int n) { var result = cutRod(p, n); while (n > 0) { System.out.println(result.getSizes()[n]); n = n - result.getSizes()[n]; } }
The overall structure of the code remains intact, but again we're burdened with extra ceremony. We have to declare input and output types, and call that awkward getSizes method to retrieve the array of cut sizes.
It's possible that my Java isn't perfectly idiomatic. After all, although I've read many books with Java examples over the years, I rarely write Java code. Additionally, you may argue that static methods exhibit a code smell like Feature Envy. I might agree, but the purpose of the current example is to examine how easy or difficult it is to implement a particular algorithm in various languages. Now that we have an implementation in Java, we might wish to refactor to a more object-oriented design, but that's outside the scope of this article.
Given that the rod-cutting algorithm isn't the most complex algorithm that exists, we may jump to the conclusion that Java isn't that bad compared to Python. Consider, however, how the extra ceremony on display here impacts your work if you have to implement a larger algorithm, or if you need to iterate to find an algorithm on your own.
To be clear, C# would require a similar amount of ceremony, and I don't even want to think about doing this in C.
All that said, it'd be irresponsible to extrapolate from only a few examples. You'd need both more languages and more problems before it even seems reasonable to draw any conclusions. I don't, however, intend the present example to constitute a full argument. Rather, it's an illustration of an idea that I haven't pulled out of thin air.
One of the points of Zone of Ceremony is that the degree of awkwardness isn't necessarily correlated to whether types are dynamically or statically defined. While I'm sure that I miss lots of points made by 'dynamists', this is a point that I often feel is missed by that camp. One language that exemplifies that 'beyond-ceremony' zone is F#.
Translation to F# #
If I'm right, we should be able to translate the rod-cutting pseudocode to F# with approximately the same amount of trouble than when translating to Python. How do we fare?
let cut (p : _ array) n = let r = Array.zeroCreate (n + 1) let s = Array.zeroCreate (n + 1) r[0] <- 0 for j = 1 to n do let mutable q = Int32.MinValue for i = 1 to j do if q < p[i] + r[j - i] then q <- p[i] + r[j - i] s[j] <- i r[j] <- q r, s
Fairly well, as it turns out, although we do have to annotate p by indicating that it's an array. Still, the underscore in front of the array keyword indicates that we're happy to let the compiler infer the type of array (which is int array).
(We can get around that issue by writing Array.item i p instead of p[i], but that's verbose in a different way.)
Had we chosen to instead implement the algorithm based on an input list or map, we wouldn't have needed the type hint. One could therefore argue that the reason that the hint is even required is because arrays aren't the most idiomatic data structure for a functional language like F#.
Otherwise, I don't find that this translation was much harder than translating to Python, and I personally prefer for j = 1 to n do over for j in range(1, n + 1):.
We also need to add the mutable keyword to allow q to change during the loop. You could argue that this is another example of additional ceremony, While I agree, it's not much related to static versus dynamic typing, but more to how values are immutable by default in F#. If I recall correctly, JavaScript similarly distinguishes between let, var, and const.
Translating Print-Cut-Rod-Solution requires, again due to values being immutable by default, a bit more effort than Python, but not much:
let printSolution p n = let _, s = cut p n let mutable n = n while n > 0 do printfn "%i" s[n] n <- n - s[n]
I had to shadow the n parameter with a mutable variable to stay as close to the pseudocode as possible. Again, one may argue that the overall problem here isn't the static type system, but that programming based on mutation isn't idiomatic for F# (or other functional programming languages). As you'll see in the next article, a more idiomatic implementation is even simpler than this one.
Notice, however, that the printSolution action requires no type declarations or annotations.
Let's see it all in use:
> let p = [|0; 1; 5; 8; 9; 10; 17; 17; 20; 24; 30|];; val p: int array = [|0; 1; 5; 8; 9; 10; 17; 17; 20; 24; 30|] > Rod.printSolution p 7;; 1 6
This little interactive session reproduces the example illustrated in the beginning of this article, when given the price array from the book and a rod of size 7, the solution printed indicates cuts at positions 1 and 6.
I find it telling that the translation to F# is on par with the translation to Python, even though the structure of the pseudocode is quite imperative.
Conclusion #
You could, perhaps, say that if your mindset is predominantly imperative, implementing an algorithm using Python is likely easier than both F# or Java. If, on the other hand, you're mostly in an implementation mindset, but not strongly attached to whether the implementation should be imperative, object-oriented, or functional, I'd offer the conjecture that a language like F# is as implementation-friendly as a language like Python.
If, on the other hand, you're more focused on encapsulating and documenting how an existing API works, perhaps that shift of perspective suggests another evaluation of dynamically versus statically typed languages.
In any case, the F# code shown here is hardly idiomatic, so it might be illuminating to see what happens if we refactor it.
Next: Encapsulating rod-cutting.
A restaurant sandwich
An Impureim Sandwich example in C#.
When learning functional programming (FP) people often struggle with how to organize code. How do you discern and maintain purity? How do you do Dependency Injection in FP? What does a functional architecture look like?
A common FP design pattern is the Impureim Sandwich. The entry point of an application is always impure, so you push all impure actions to the boundary of the system. This is also known as Functional Core, Imperative Shell. If you have a micro-operation-based architecture, which includes all web-based systems, you can often get by with a 'sandwich'. Perform impure actions to collect all the data you need. Pass all data to a pure function. Finally, use impure actions to handle the referentially transparent return value from the pure function.
No design pattern applies universally, and neither does this one. In my experience, however, it's surprisingly often possible to apply this architecture. We're far past the Pareto principle's 80 percent.
Examples may help illustrate the pattern, as well as explore its boundaries. In this article you'll see how I refactored an entry point of a REST API, specifically the PUT handler in the sample code base that accompanies Code That Fits in Your Head.
Starting point #
As discussed in the book, the architecture of the sample code base is, in fact, Functional Core, Imperative Shell. This isn't, however, the main theme of the book, and the code doesn't explicitly apply the Impureim Sandwich. In spirit, that's actually what's going on, but it isn't clear from looking at the code. This was a deliberate choice I made, because I wanted to highlight other software engineering practices. This does have the effect, though, that the Impureim Sandwich is invisible.
For example, the book follows the 80/24 rule closely. This was a didactic choice on my part. Most code bases I've seen in the wild have far too big methods, so I wanted to hammer home the message that it's possible to develop and maintain a non-trivial code base with small code blocks. This meant, however, that I had to split up HTTP request handlers (in ASP.NET known as action methods on Controllers).
The most complex HTTP handler is the one that handles PUT requests for reservations. Clients use this action when they want to make changes to a restaurant reservation.
The action method actually invoked by an HTTP request is this Put method:
[HttpPut("restaurants/{restaurantId}/reservations/{id}")] public async Task<ActionResult> Put( int restaurantId, string id, ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); if (!Guid.TryParse(id, out var rid)) return new NotFoundResult(); Reservation? reservation = dto.Validate(rid); if (reservation is null) return new BadRequestResult(); var restaurant = await RestaurantDatabase .GetRestaurant(restaurantId).ConfigureAwait(false); if (restaurant is null) return new NotFoundResult(); return await TryUpdate(restaurant, reservation).ConfigureAwait(false); }
Since I, for pedagogical reasons, wanted to fit each method inside an 80x24 box, I made a few somewhat unnatural design choices. The above code is one of them. While I don't consider it completely indefensible, this method does a bit of up-front input validation and verification, and then delegates execution to the TryUpdate method.
This may seem all fine and dandy until you realize that the only caller of TryUpdate is that Put method. A similar thing happens in TryUpdate: It calls a method that has only that one caller. We may try to inline those two methods to see if we can spot the Impureim Sandwich.
Inlined Transaction Script #
Inlining those two methods leave us with a larger, Transaction Script-like entry point:
[HttpPut("restaurants/{restaurantId}/reservations/{id}")] public async Task<ActionResult> Put( int restaurantId, string id, ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); if (!Guid.TryParse(id, out var rid)) return new NotFoundResult(); Reservation? reservation = dto.Validate(rid); if (reservation is null) return new BadRequestResult(); var restaurant = await RestaurantDatabase .GetRestaurant(restaurantId).ConfigureAwait(false); if (restaurant is null) return new NotFoundResult(); using var scope = new TransactionScope( TransactionScopeAsyncFlowOption.Enabled); var existing = await Repository .ReadReservation(restaurant.Id, reservation.Id) .ConfigureAwait(false); if (existing is null) return new NotFoundResult(); var reservations = await Repository .ReadReservations(restaurant.Id, reservation.At) .ConfigureAwait(false); reservations = reservations.Where(r => r.Id != reservation.Id).ToList(); var now = Clock.GetCurrentDateTime(); var ok = restaurant.MaitreD.WillAccept( now, reservations, reservation); if (!ok) return NoTables500InternalServerError(); await Repository.Update(restaurant.Id, reservation) .ConfigureAwait(false); scope.Complete(); return new OkObjectResult(reservation.ToDto()); }
While I've definitely seen longer methods in the wild, this variation is already so big that it no longer fits on my laptop screen. I have to scroll up and down to read the whole thing. When looking at the bottom of the method, I have to remember what was at the top, because I can no longer see it.
A major point of Code That Fits in Your Head is that what limits programmer productivity is human cognition. If you have to scroll your screen because you can't see the whole method at once, does that fit in your brain? Chances are, it doesn't.
Can you spot the Impureim Sandwich now?
If you can't, that's understandable. It's not really clear because there's quite a few small decisions being made in this code. You could argue, for example, that this decision is referentially transparent:
if (existing is null) return new NotFoundResult();
These two lines of code are deterministic and have no side effects. The branch only returns a NotFoundResult when existing is null. Additionally, these two lines of code are surrounded by impure actions both before and after. Is this the Sandwich, then?
No, it's not. This is how idiomatic imperative code looks. To borrow a diagram from another article, pure and impure code is interleaved without discipline:

Even so, the above Put method implements the Functional Core, Imperative Shell architecture. The Put method is the Imperative Shell, but where's the Functional Core?
Shell perspective #
One thing to be aware of is that when looking at the Imperative Shell code, the Functional Core is close to invisible. This is because it's typically only a single function call.
In the above Put method, this is the Functional Core:
var ok = restaurant.MaitreD.WillAccept( now, reservations, reservation); if (!ok) return NoTables500InternalServerError();
It's only a few lines of code, and had I not given myself the constraint of staying within an 80 character line width, I could have instead laid it out like this and inlined the ok flag:
if (!restaurant.MaitreD.WillAccept(now, reservations, reservation)) return NoTables500InternalServerError();
Now that I try this, in fact, it turns out that this actually still stays within 80 characters. To be honest, I don't know exactly why I had that former code instead of this, but perhaps I found the latter alternative too dense. Or perhaps I simply didn't think of it. Code is rarely perfect. Usually when I revisit a piece of code after having been away from it for some time, I find some thing that I want to change.
In any case, that's beside the point. What matters here is that when you're looking through the Imperative Shell code, the Functional Core looks insignificant. Blink and you'll miss it. Even if we ignore all the other small pure decisions (the if statements) and pretend that we already have an Impureim Sandwich, from this viewpoint, the architecture looks like this:

It's tempting to ask, then: What's all the fuss about? Why even bother?
This is a natural experience for a code reader. After all, if you don't know a code base well, you often start at the entry point to try to understand how the application handles a certain stimulus. Such as an HTTP PUT request. When you do that, you see all of the Imperative Shell code before you see the Functional Core code. This could give you the wrong impression about the balance of responsibility.
After all, code like the above Put method has inlined most of the impure code so that it's right in your face. Granted, there's still some code hiding behind, say, Repository.ReadReservations, but a substantial fraction of the imperative code is visible in the method.
On the other hand, the Functional Core is just a single function call. If we inlined all of that code, too, the picture might rather look like this:

This obviously depends on the de-facto ratio of pure to imperative code. In any case, inlining the pure code is a thought experiment only, because the whole point of functional architecture is that a referentially transparent function fits in your head. Regardless of the complexity and amount of code hiding behind that MaitreD.WillAccept function, the return value is equal to the function call. It's the ultimate abstraction.
Standard combinators #
As I've already suggested, the inlined Put method looks like a Transaction Script. The cyclomatic complexity fortunately hovers on the magical number seven, and branching is exclusively organized around Guard Clauses. Apart from that, there are no nested if statements or for loops.
Apart from the Guard Clauses, this mostly looks like a procedure that runs in a straight line from top to bottom. The exception is all those small conditionals that may cause the procedure to exit prematurely. Conditions like this:
if (!Guid.TryParse(id, out var rid)) return new NotFoundResult();
or
if (reservation is null) return new BadRequestResult();
Such checks occur throughout the method. Each of them are actually small pure islands amidst all the imperative code, but each is ad hoc. Each checks if it's possible for the procedure to continue, and returns a kind of error value if it decides that it's not.
Is there a way to model such 'derailments' from the main flow?
If you've ever encountered Scott Wlaschin's Railway Oriented Programming you may already see where this is going. Railway-oriented programming is a fantastic metaphor, because it gives you a way to visualize that you have, indeed, a main track, but then you have a side track that you may shuffle some trains too. And once the train is on the side track, it can't go back to the main track.
That's how the Either monad works. Instead of all those ad-hoc if statements, we should be able to replace them with what we may call standard combinators. The most important of these combinators is monadic bind. Composing a Transaction Script like Put with standard combinators will 'hide away' those small decisions, and make the Sandwich nature more apparent.
If we had had pure code, we could just have composed Either-valued functions. Unfortunately, most of what's going on in the Put method happens in a Task-based context. Thankfully, Either is one of those monads that nest well, implying that we can turn the combination into a composed TaskEither monad. The linked article shows the core TaskEither SelectMany implementations.
The way to encode all those small decisions between 'main track' or 'side track', then, is to wrap 'naked' values in the desired Task<Either<L, R>> container:
Task.FromResult(id.TryParseGuid().OnNull((ActionResult)new NotFoundResult()))
This little code snippet makes use of a few small building blocks that we also need to introduce. First, .NET's standard TryParse APIs don't, compose, but since they're isomorphic to Maybe-valued functions, you can write an adapter like this:
public static Guid? TryParseGuid(this string candidate) { if (Guid.TryParse(candidate, out var guid)) return guid; else return null; }
In this code base, I treat nullable reference types as equivalent to the Maybe monad, but if your language doesn't have that feature, you can use Maybe instead.
To implement the Put method, however, we don't want nullable (or Maybe) values. We need Either values, so we may introduce a natural transformation:
public static Either<L, R> OnNull<L, R>(this R? candidate, L left) where R : struct { if (candidate.HasValue) return Right<L, R>(candidate.Value); return Left<L, R>(left); }
In Haskell one might just make use of the built-in Maybe catamorphism:
ghci> maybe (Left "boo!") Right $ Just 123 Right 123 ghci> maybe (Left "boo!") Right $ Nothing Left "boo!"
Such conversions from Maybe to Either hover just around the Fairbairn threshold, but since we are going to need it more than once, it makes sense to add a specialized OnNull transformation to the C# code base. The one shown here handles nullable value types, but the code base also includes an overload that handles nullable reference types. It's almost identical.
Support for query syntax #
There's more than one way to consume monadic values in C#. While many C# developers like LINQ, most seem to prefer the familiar method call syntax; that is, just call the Select, SelectMany, and Where methods as the normal extension methods they are. Another option, however, is to use query syntax. This is what I'm aiming for here, since it'll make it easier to spot the Impureim Sandwich.
You'll see the entire sandwich later in the article. Before that, I'll highlight details and explain how to implement them. You can always scroll down to see the end result, and then scroll back here, if that's more to your liking.
The sandwich starts by parsing the id into a GUID using the above building blocks:
var sandwich = from rid in Task.FromResult(id.TryParseGuid().OnNull((ActionResult)new NotFoundResult()))
It then immediately proceeds to Validate (parse, really) the dto into a proper Domain Model:
from reservation in dto.Validate(rid).OnNull((ActionResult)new BadRequestResult())
Notice that the second from expression doesn't wrap the result with Task.FromResult. How does that work? Is the return value of dto.Validate already a Task? No, this works because I added 'degenerate' SelectMany overloads:
public static Task<Either<L, R1>> SelectMany<L, R, R1>( this Task<Either<L, R>> source, Func<R, Either<L, R1>> selector) { return source.SelectMany(x => Task.FromResult(selector(x))); } public static Task<Either<L, R1>> SelectMany<L, U, R, R1>( this Task<Either<L, R>> source, Func<R, Either<L, U>> k, Func<R, U, R1> s) { return source.SelectMany(x => k(x).Select(y => s(x, y))); }
Notice that the selector only produces an Either<L, R1> value, rather than Task<Either<L, R1>>. This allows query syntax to 'pick up' the previous value (rid, which is 'really' a Task<Either<ActionResult, Guid>>) and continue with a function that doesn't produce a Task, but rather just an Either value. The first of these two overloads then wraps that Either value and wraps it with Task.FromResult. The second overload is just the usual ceremony that enables query syntax.
Why, then, doesn't the sandwich use the same trick for rid? Why does it explicitly call Task.FromResult?
As far as I can tell, this is because of type inference. It looks as though the C# compiler infers the monad's type from the first expression. If I change the first expression to
from rid in id.TryParseGuid().OnNull((ActionResult)new NotFoundResult())
the compiler thinks that the query expression is based on Either<L, R>, rather than Task<Either<L, R>>. This means that once we run into the first Task value, the entire expression no longer works.
By explicitly wrapping the first expression in a Task, the compiler correctly infers the monad we'd like it to. If there's a more elegant way to do this, I'm not aware of it.
Values that don't fail #
The sandwich proceeds to query various databases, using the now-familiar OnNull combinators to transform nullable values to Either values.
from restaurant in RestaurantDatabase .GetRestaurant(restaurantId) .OnNull((ActionResult)new NotFoundResult()) from existing in Repository .ReadReservation(restaurant.Id, reservation.Id) .OnNull((ActionResult)new NotFoundResult())
This works like before because both GetRestaurant and ReadReservation are queries that may fail to return a value. Here's the interface definition of ReadReservation:
Task<Reservation?> ReadReservation(int restaurantId, Guid id);
Notice the question mark that indicates that the result may be null.
The GetRestaurant method is similar.
The next query that the sandwich has to perform, however, is different. The return type of the ReadReservations method is Task<IReadOnlyCollection<Reservation>>. Notice that the type contained in the Task is not nullable. Barring database connection errors, this query can't fail. If it finds no data, it returns an empty collection.
Since the value isn't nullable, we can't use OnNull to turn it into a Task<Either<L, R>> value. We could try to use the Right creation function for that.
public static Either<L, R> Right<L, R>(R right) { return Either<L, R>.Right(right); }
This works, but is awkward:
from reservations in Repository .ReadReservations(restaurant.Id, reservation.At) .Traverse(rs => Either.Right<ActionResult, IReadOnlyCollection<Reservation>>(rs))
The problem with calling Either.Right is that while the compiler can infer which type to use for R, it doesn't know what the L type is. Thus, we have to tell it, and we can't tell it what L is without also telling it what R is. Even though it already knows that.
In such scenarios, the F# compiler can usually figure it out, and GHC always can (unless you add some exotic language extensions to your code). C# doesn't have any syntax that enables you to tell the compiler about only the type that it doesn't know about, and let it infer the rest.
All is not lost, though, because there's a little trick you can use in cases such as this. You can let the C# compiler infer the R type so that you only have to tell it what L is. It's a two-stage process. First, define an extension method on R:
public static RightBuilder<R> ToRight<R>(this R right) { return new RightBuilder<R>(right); }
The only type argument on this ToRight method is R, and since the right parameter is of the type R, the C# compiler can always infer the type of R from the type of right.
What's RightBuilder<R>? It's this little auxiliary class:
public sealed class RightBuilder<R> { private readonly R right; public RightBuilder(R right) { this.right = right; } public Either<L, R> WithLeft<L>() { return Either.Right<L, R>(right); } }
The code base for Code That Fits in Your Head was written on .NET 3.1, but today you could have made this a record instead. The only purpose of this class is to break the type inference into two steps so that the R type can be automatically inferred. In this way, you only need to tell the compiler what the L type is.
from reservations in Repository .ReadReservations(restaurant.Id, reservation.At) .Traverse(rs => rs.ToRight().WithLeft<ActionResult>())
As indicated, this style of programming isn't language-neutral. Even if you find this little trick neat, I'd much rather have the compiler just figure it out for me. The entire sandwich query expression is already defined as working with Task<Either<ActionResult, R>>, and the L type can't change like the R type can. Functional compilers can figure this out, and while I intend this article to show object-oriented programmers how functional programming sometimes work, I don't wish to pretend that it's a good idea to write code like this in C#. I've covered that ground already.
Not surprisingly, there's a mirror-image ToLeft/WithRight combo, too.
Working with Commands #
The ultimate goal with the Put method is to modify a row in the database. The method to do that has this interface definition:
Task Update(int restaurantId, Reservation reservation);
I usually call that non-generic Task class for 'asynchronous void' when explaining it to non-C# programmers. The Update method is an asynchronous Command.
Task and void aren't legal values for use with LINQ query syntax, so you have to find a way to work around that limitation. In this case I defined a local helper method to make it look like a Query:
async Task<Reservation> RunUpdate(int restaurantId, Reservation reservation, TransactionScope scope) { await Repository.Update(restaurantId, reservation).ConfigureAwait(false); scope.Complete(); return reservation; }
It just echoes back the reservation parameter once the Update has completed. This makes it composable in the larger query expression.
You'll probably not be surprised when I tell you that both F# and Haskell handle this scenario gracefully, without requiring any hoop-jumping.
Full sandwich #
Those are all the building block. Here's the full sandwich definition, colour-coded like the examples in Impureim sandwich.
Task<Either<ActionResult, OkObjectResult>> sandwich = from rid in Task.FromResult( id.TryParseGuid().OnNull((ActionResult)new NotFoundResult())) from reservation in dto.Validate(rid).OnNull( (ActionResult)new BadRequestResult()) from restaurant in RestaurantDatabase .GetRestaurant(restaurantId) .OnNull((ActionResult)new NotFoundResult()) from existing in Repository .ReadReservation(restaurant.Id, reservation.Id) .OnNull((ActionResult)new NotFoundResult()) from reservations in Repository .ReadReservations(restaurant.Id, reservation.At) .Traverse(rs => rs.ToRight().WithLeft<ActionResult>()) let now = Clock.GetCurrentDateTime() let reservations2 = reservations.Where(r => r.Id != reservation.Id) let ok = restaurant.MaitreD.WillAccept( now, reservations2, reservation) from reservation2 in ok ? reservation.ToRight().WithLeft<ActionResult>() : NoTables500InternalServerError().ToLeft().WithRight<Reservation>() from reservation3 in RunUpdate(restaurant.Id, reservation2, scope) .Traverse(r => r.ToRight().WithLeft<ActionResult>()) select new OkObjectResult(reservation3.ToDto());
As is evident from the colour-coding, this isn't quite a sandwich. The structure is honestly more accurately depicted like this:

As I've previously argued, while the metaphor becomes strained, this still works well as a functional-programming architecture.
As defined here, the sandwich value is a Task that must be awaited.
Either<ActionResult, OkObjectResult> either = await sandwich.ConfigureAwait(false); return either.Match(x => x, x => x);
By awaiting the task, we get an Either value. The Put method, on the other hand, must return an ActionResult. How do you turn an Either object into a single object?
By pattern matching on it, as the code snippet shows. The L type is already an ActionResult, so we return it without changing it. If C# had had a built-in identity function, I'd used that, but idiomatically, we instead use the x => x lambda expression.
The same is the case for the R type, because OkObjectResult inherits from ActionResult. The identity expression automatically performs the type conversion for us.
This, by the way, is a recurring pattern with Either values that I run into in all languages. You've essentially computed an Either<T, T>, with the same type on both sides, and now you just want to return whichever T value is contained in the Either value. You'd think this is such a common pattern that Haskell has a nice abstraction for it, but even Hoogle fails to suggest a commonly-accepted function that does this. Apparently, either id id is considered below the Fairbairn threshold, too.
Conclusion #
This article presents an example of a non-trivial Impureim Sandwich. When I introduced the pattern, I gave a few examples. I'd deliberately chosen these examples to be simple so that they highlighted the structure of the idea. The downside of that didactic choice is that some commenters found the examples too simplistic. Therefore, I think that there's value in going through more complex examples.
The code base that accompanies Code That Fits in Your Head is complex enough that it borders on the realistic. It was deliberately written that way, and since I assume that the code base is familiar to readers of the book, I thought it'd be a good resource to show how an Impureim Sandwich might look. I explicitly chose to refactor the Put method, since it's easily the most complicated process in the code base.
The benefit of that code base is that it's written in a programming language that reach a large audience. Thus, for the reader curious about functional programming I thought that this could also be a useful introduction to some intermediate concepts.
As I've commented along the way, however, I wouldn't expect anyone to write production C# code like this. If you're able to do this, you're also able to do it in a language better suited for this programming paradigm.
Implementation and usage mindsets
A one-dimensional take on the enduring static-versus-dynamic debate.
It recently occurred to me that one possible explanation for the standing, and probably never-ending, debate about static versus dynamic types may be that each camp have disjoint perspectives on the kinds of problems their favourite languages help them solve. In short, my hypothesis is that perhaps lovers of dynamically-typed languages often approach a problem from an implementation mindset, whereas proponents of static types emphasize usage.

I'll expand on this idea here, and then provide examples in two subsequent articles.
Background #
For years I've struggled to understand 'the other side'. While I'm firmly in the statically typed camp, I realize that many highly skilled programmers and thought leaders enjoy, or get great use out of, dynamically typed languages. This worries me, because it might indicate that I'm stuck in a local maximum.
In other words, just because I, personally, prefer static types, it doesn't follow that static types are universally better than dynamic types.
In reality, it's probably rather the case that we're dealing with a false dichotomy, and that the problem is really multi-dimensional.
"Let me stop you right there: I don't think there is a real dynamic typing versus static typing debate.
"What such debates normally are is language X vs language Y debates (where X happens to be dynamic and Y happens to be static)."
Even so, I can't help thinking about such things. Am I missing something?
For the past few years, I've dabbled with Python to see what writing in a popular dynamically typed language is like. It's not a bad language, and I can clearly see how it's attractive. Even so, I'm still frustrated every time I return to some Python code after a few weeks or more. The lack of static types makes it hard for me to pick up, or revisit, old code.
A question of perspective? #
Whenever I run into a difference of opinion, I often interpret it as a difference in perspective. Perhaps it's my academic background as an economist, but I consider it a given that people have different motivations, and that incentives influence actions.
A related kind of analysis deals with problem definitions. Are we even trying to solve the same problem?
I've discussed such questions before, but in a different context. Here, it strikes me that perhaps programmers who gravitate toward dynamically typed languages are focused on another problem than the other group.
Again, I'd like to emphasize that I don't consider the world so black and white in reality. Some developers straddle the two camps, and as the above Kevlin Henney quote suggests, there really aren't only two kinds of languages. C and Haskell are both statically typed, but the similarities stop there. Likewise, I don't know if it's fair to put JavaScript and Clojure in the same bucket.
That said, I'd still like to offer the following hypothesis, in the spirit that although all models are wrong, some are useful.
The idea is that if you're trying to solve a problem related to implementation, dynamically typed languages may be more suitable. If you're trying to implement an algorithm, or even trying to invent one, a dynamic language seems useful. One year, I did a good chunk of Advent of Code in Python, and didn't find it harder than in Haskell. (I ultimately ran out of steam for reasons unrelated to Python.)
On the other hand, if your main focus may be usage of your code, perhaps you'll find a statically typed language more useful. At least, I do. I can use the static type system to communicate how my APIs work. How to instantiate my classes. How to call my functions. How return values are shaped. In other words, the preconditions, invariants, and postconditions of my reusable code: Encapsulation.
Examples #
Some examples may be in order. In the next two articles, I'll first examine how easy it is to implement an algorithm in various programming languages. Then I'll discuss how to encapsulate that algorithm.
The articles will both discuss the rod-cutting problem from Introduction to Algorithms, but I'll introduce the problem in the next article.
Conclusion #
I'd be naive if I believed that a single model can fully explain why some people prefer dynamically typed languages, and others rather like statically typed languages. Even so, suggesting a model helps me understand how to analyze problems.
My hypothesis is that dynamically typed languages may be suitable for implementing algorithms, whereas statically typed languages offer better encapsulation.
This may be used as a heuristic for 'picking the right tool for the job'. If I need to suss out an algorithm, perhaps I should do it in Python. If, on the other hand, I need to publish a reusable library, perhaps Haskell is a better choice.
Next: Implementing rod-cutting.

Comments
An interesting insight, but if you consider that the compiler is effectively an additional test suit that is verifying the types are being used correctly, that extra compilation time is really just a whole suite of tests that you didn't have to write. I can't help but wonder how long it would take to manually implement all the tests that would be required to satisfy those checks in Python, and how much slower the Python test suite would then be.
Like you, I have a strong bias for typesafe languages (or at least moderately typesafe ones). The way I've always explained it is as follows: Developers tend to work faster when writing with dynamic typed languages because they don't have to explain as much to a compiler. This literally means less code to write. However, because the developer hasen't fully explained themself, any follow-on developer does not have as much context to work with.
After all, whether the language requires it or not, the developers need to define and consider types. The only question is, do they have to write it down
Daniel, thank you for writing. I'm well aware that a type checker is a 'first line of defence', and I agree that if we truly had to replicate everything that a type checker does, as tests, it would take a long time. It would take a long time to write all those tests, and it would probably also take a long time to execute them all.
That said, I think that any sane proponent of dynamically typed languages would counter that that's an unreasonable demand. After all, in most cases, it's hardly the case that the code was written by a monkey with a typewriter, but rather by a well-meaning human who did his or her best to write correct code.
In the end, however, it's all a question about context. How important is correctness, after all? Dan North once kindly pointed out to me that in many cases, the software owner doesn't even know what he or she wants. It's only through a series of iterations that we learn what a business system is supposed to do. Until we reach that point, correctness is, at best, a secondary priority. On the other hand, you should really test your outer space proble software.
But you're right. The types are still there, either way.
The last word in this debate are hardly said yet, but you may also find my recent article series Implementation and usage mindsets interesting.